基于神经网络的光纤陀螺温度漂移误差建模与补偿

张和杰，郭士荦

（1.海军装备部 舰船技术保障部，北京100086；2.海军工程大学 导航工程系，武汉430033）

基于神经网络的光纤陀螺温度漂移误差建模与补偿

张和杰1，郭士荦2

（1.海军装备部 舰船技术保障部，北京100086；2.海军工程大学 导航工程系，武汉430033）

摘要：光纤陀螺（FOG）温度漂移误差是影响其输出精度的主要误差源之一，在实际应用中必须对光纤陀螺温度漂移误差进行适当补偿。传统的最小二乘法等线性补偿方法很难满足补偿精度的要求且适用性较差，利用BP及RBF神经网络分别建立非线性光纤陀螺温度漂移误差模型，可以有效提高补偿精度，使用FOG温箱实测数据对最小二乘模型及神经网络补偿模型进行了测试对比，验证了基于神经网络的非线性补偿算法在FOG温度漂移补偿中的有效性。

关键词：光纤陀螺；温度漂移补偿；神经网络；非线性模型

0　引言

光纤陀螺通过多匝线圈增大光线传播路程，以提高光纤传感环圈的角速度灵敏度。1980年D. M.Shupe首次提出，在光纤陀螺某段光纤上存在变化的温度扰动时，会导致光纤折射率发生变化，造成两束反向传播的光束在经过这段光纤时产生不同的相位变化，引起非互易性的相移。这种相移与萨格奈克相移叠加在一起会造成陀螺输出信号的失真。这种温度漂移是光纤陀螺误差补偿中最棘手的问题之一。

目前针对FOG温度漂移模型的建立和辨识方法主要有最小二乘拟合、神经网络建模、模糊模型辨识等，神经网络因其使用方便，补偿精度普遍可以达到使用要求，成为光纤陀螺温度漂移模型建立和温度漂移误差补偿的主要技术手段之一。

文献[2]从理论上分析了FOG温度漂移误差产生的原理，设计了FOG静态温度漂移实验方案并进行了测试，使用了最小二乘法对数据建立1～7次模型，但由于采用多项式线性拟合的方法进行建模与补偿，难以准确描述FOG温度特性的非线性特征，使用最小二乘模型无法得到最优的补偿效果；文献[3]综述了国内外近年来对光纤陀螺温度漂移误差的补偿进行的各项工作，主要包括光纤陀螺机理结构的改善、硬件温控措施及软件建模补偿等方面的内容，对几类神经网络建模方法进行了概述，但没有进行仿真验证；文献[5]采用恒温静态试验数据辨识模糊规则库，通过模糊推理的方法实现FOG温度漂移的自动在线补偿，不足在于该模型仅适用于近似恒温环境下的FOG温度漂移补偿，在外部工作环境温度变化较大的情况适应性不理想。

本文对Shupe非互易性原理、基于最小二乘法的线性补偿方案以及基于BP神经网络与RBF神经网络的非线性补偿方案分别进行了深入研究，利用光纤陀螺温度温箱实测数据对三种补偿方法分别进行验证对比。结果表明非线性神经网络补偿方案对大温度扰动环境下的FOG温度漂移数据具有较好的补偿效果。

1　Shupe非互易性

光纤线圈中不均匀的温度变化使正反两束光波产生非互易性的相位变化，引入萨格奈克效应之外的叠加相移。这种温度变化引起的干扰被称为Shupe非互易性[1]，对光纤陀螺输出精度非常有害。

设光波沿长度为L的光纤线圈传播，相移延迟与相关传播常数之间的关系可以表示为[1]：

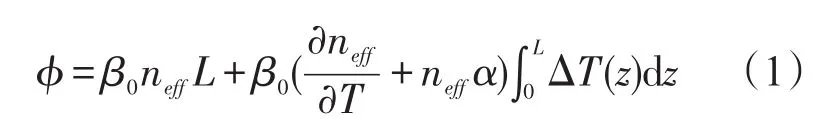
其中 β0=2π/为真空中光线的传播常数，L为光纤线圈长度，neff为光纤线圈折射率，为折射率的温度变化系数，α为光纤材料的温度膨胀系数，ΔT(z)为距离光纤线圈始端长度为z处的温度变化梯度。

假设光纤线圈中距离始端z处的线段温度变化梯度为ΔT(z,t)（即ΔT是距离与时间的函数）。假设正反两束干涉光分别以顺时针（CW）和逆时针（CCW）方向到达线圈始端的时刻为t，则它们通过距离始端z处的时刻见式（2）。

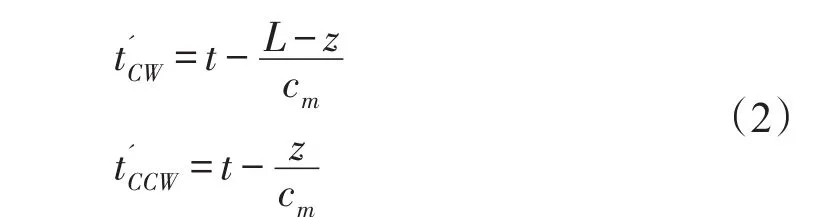
式中cm=c/neff为光线传播速度。

由（1）式可知这种温度梯度的变化引起的相移为：

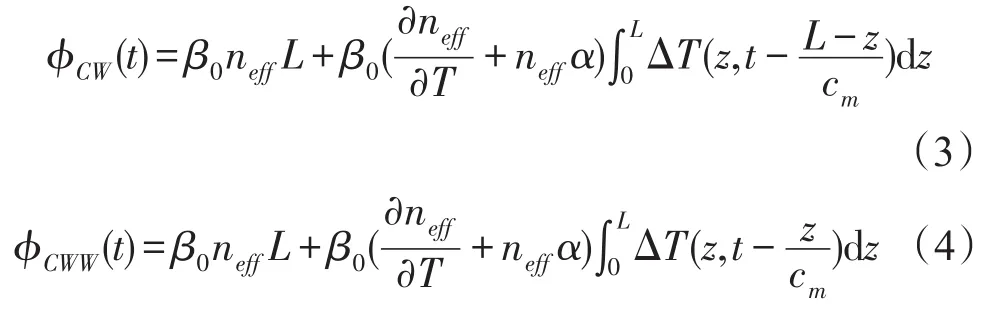
式（3）－（4）得温度在光纤线圈上的梯度分布造成的两束光波相位差为：

通过式（5）就可以得到光纤陀螺温度漂移误差。可以看出当温度扰动位于光纤线圈中点对称分布时，z=，两束光波的温度漂移误差刚好抵消，反之温度扰动不对称度越大，温度漂移误差也越大。

2　基于最小二乘法的FOG温度漂移补偿

最小二乘法（最小平方法）的基本原理是以最小化误差平方和的原则来确定最优的匹配函数。或者说，若利用最小二乘法对给定数组(Xi,Yi)(i=1,2,...,n)，进行拟合，那么必须找到一个最优函数关系Φ，使其对于Xi的函数值与Φ(Xi)与Yi之差的平方和E2=Σ[Φ(Xi)-Yi]2最小，表明在所有Xi的函数关系中该函数与Yi的距离最近。那么通过该函数关系得到的对Yi的预测值与实际值之间的偏差即为最小。函数 Φ(Xi)是对模型(Xi,Yi)(i=1,2,...,n)的最小二乘拟合。

最小二乘法是数据拟合中的常用方法，下面首先用该方法对光纤陀螺温度漂移进行建模。

根据对实测数据的经验性分析，首先对温度漂移建立多项式模型如下：

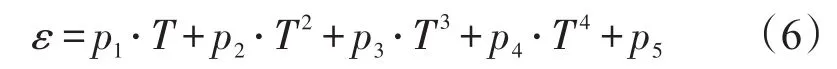
式中ε为光纤陀螺输出的带有温度漂移误差的角速率， pi(i=1,2,3,4,5)为误差模型参数，T为光纤陀螺工作环境温度。

3　BP神经网络建模

神经网络良好的非线性拟合特性使其适用于多种非线性拟合的应用。而FOG温度漂移由于受到多种因素的影响明显具有非线性特性，因此神经网络模型在FOG温度漂移误差补偿中可以得到良好的应用。常用神经网络有BP神经网络及RBF神经网络。

BP神经网络也叫做多层网络的误差反向传播算法（Error Back–Propagation Training），其原理是通过最优拟合算法，调节网络连接权值以保证网络误差极小[3]。通常BP神经网络具有输入层、隐含层、输出层三层结构，如图1所示。

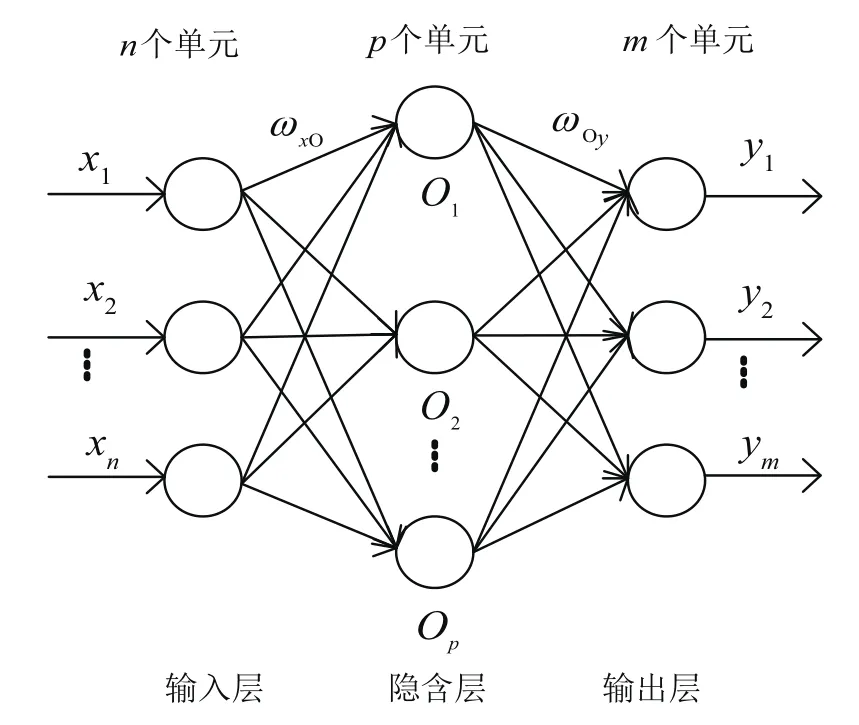
图1　BP神经网络基本结构Fig.1 Basic structure of the BP neural network

BP神经网络的工作过程分为正向传播和反向传播两个部分。正向传播过程中，每一层神经元只影响下一层神经元的结构，通过激活函数得到输出端的输出值，当输出值与理想输出值偏差较大或者不满足误差要求时，就要将误差信号转入反向传播过程对神经网络进行校正，不断地修改各层神经元的权值使得网络输出值逐渐逼近理想输出值，直到输出误差达到限定的水平。

图1所示的BP神经网络有n个输入单元、m个输出单元和一个p节点的隐含层，则隐含层输出与网络层输出分别为式（7）和式（8）。

隐含层：

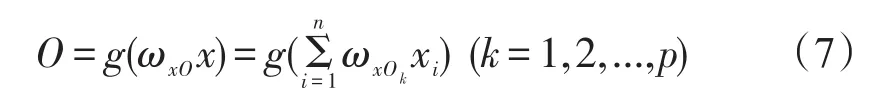
输出层：

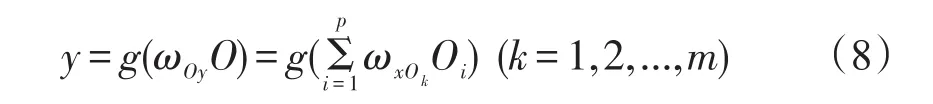
式中xi(i=1,2,...,n)为网络的输入值，Oi(i=1,2,...,p)为隐含层输出值，yi(i=1,2,...,m)为网络输出值，函数g称为激励函数[4]。

使用BP神经网络对光纤陀螺温度漂移误差模型进行拟合的算法流程图如图2所示。

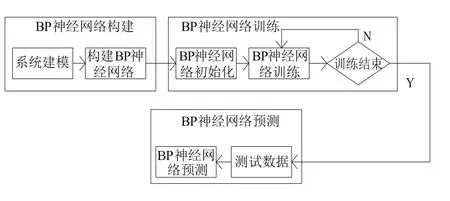
图2　BP神经网络算法流程图Fig.2 Algorithm flow chart of BP neural network

BP神经网络隐含层可以分为单隐含层和多隐含层，多隐含层由多个单隐含层组成，其预测精度较单隐含层更高，但缺点是训练时间较长，对于映射关系复杂且不要求训练速度的应用，可以使用多隐含层的BP神经网络。使用BP神经网络可以很方便地对FOG误差模型进行拟合补偿。

4　RBF神经网络建模

径向基函数（RBF，Radical Basis Function）是由Powell在1985年提出的多维空间插值的传统技术。1988年学者根据生物神经元具有局部响应这一特点，将RBF引入神经网络设计中，形成RBF神经网络。RBF神经网络是解决非线性函数的逼近问题的一个有效方法。RBF神经网络是一种三层的前向网络，第一层为输入层；第二层为隐含层，隐含层中的神经元激励函数即径向基函数是对中心点径向对称且衰减非负非线性函数；第三层为输出层，这三层结构满足输入层到输出层的非线性映射和隐含层到输出层的线性映射，从而大大加快了学习速度，有效避免了局部极小的问题。

RBF神经网络的基本原理是：径向基函数作为隐含层的基本单元，可以对输入矢量进行变换，将低维的模式输入数据变换的高维空间，使得在低维空间内线性不可分的问题在高维空间内线性可分。已经证明RBF神经网络能够以任意精度逼近任意连续函数。

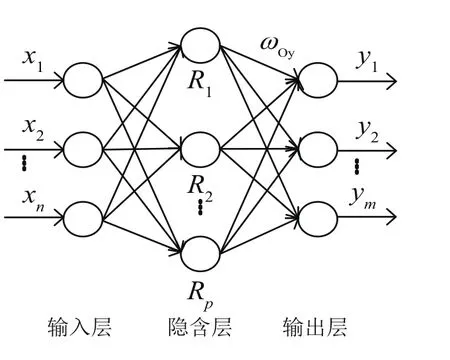
图3　RBF神经网络基本结构Fig.3 Basic structure of the RBF neural network

如图3所示是RBF神经网络基本结构，可以看到RBF神经网络与上一节用到的BP神经网络结构基本类似，都是具有三层结构。不同点在于径向基神经网络的激活函数是以输入向量和权值向量之间的距离‖dist‖作为自变量的，因此其激活函数的一般表达式为：

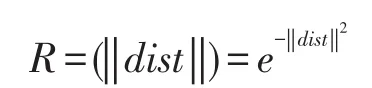
权值向量与输入向量越接近，则网络输出值越大，当输入向量和权值向量完全相等时，单个神经元输出yi为1。另外RBF神经网络与前文提到的BP神经网络的另一点区别在于，RBF神经网络的输入层仅仅起到信号连接的作用，相当于在BP神经网络中将输入层到隐含层的连接权值全部赋值为1，输入层的主要工作是采用线性优化策略对线性权进行调整，而隐含层的工作是对激活函数的参数进行调整，采用的是非线性的优化策略，学习速率较慢。

径向基神经网络中常用的激活函数是高斯函数，可以表示为：

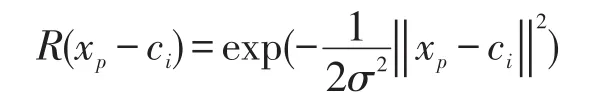
相应的网络输出见式（9）。

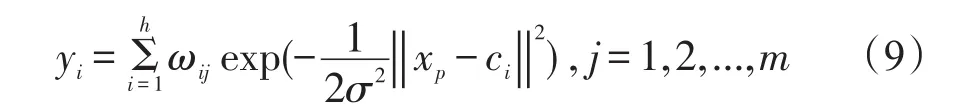
5　基于最小二乘法及神经网络的FOG温度漂移补偿

2014年3月，在国内某研究所进行了光纤陀螺温控箱数据采集试验，试验时将FOG置于静态温箱内，温度调整变化区间为－10°～35°，记录光纤陀螺输出数据，采样频率为200Hz。分别用最小二乘法、BP神经网络、RBF神经网络对该温度漂移数据进行建模及补偿，并对比补偿结果。

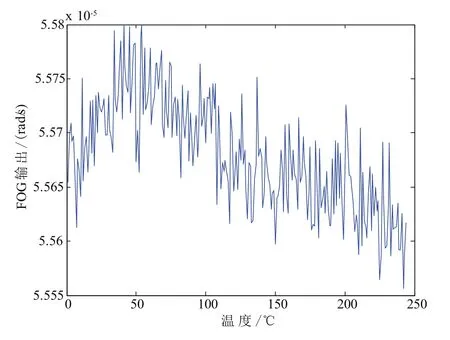
图4　FOG温箱实测数据Fig.4 Measured FOG data in incubator

图4所示为光纤陀螺温箱试验中的实测漂移数据，可以看到在-5°C～30°C变化范围光纤陀螺输出中叠加的温度漂移较大，必须进行适当补偿。

最小二乘法是最常用的数据拟合方法，其基本原理是通过最小化误差平方和来确定最优的匹配函数，在使用最小二乘法对数据进行拟合之前必须先确定与数据波动匹配较好的拟合方式，如选择指数方式拟合或者多项式方式拟合，确定拟合方式后再对拟合函数的参数进行求解；基于神经网络的非线性拟合具有逼近能力强、精度高、结构灵活等优势，不需要事先确定拟合函数，可以在最大程度上逼近训练数据的变化趋势。

在相同的试验条件下采集另一组光纤陀螺温度漂移数据对本文提出的三种误差模型进行测试，得到对比结果如图5～图7所示。

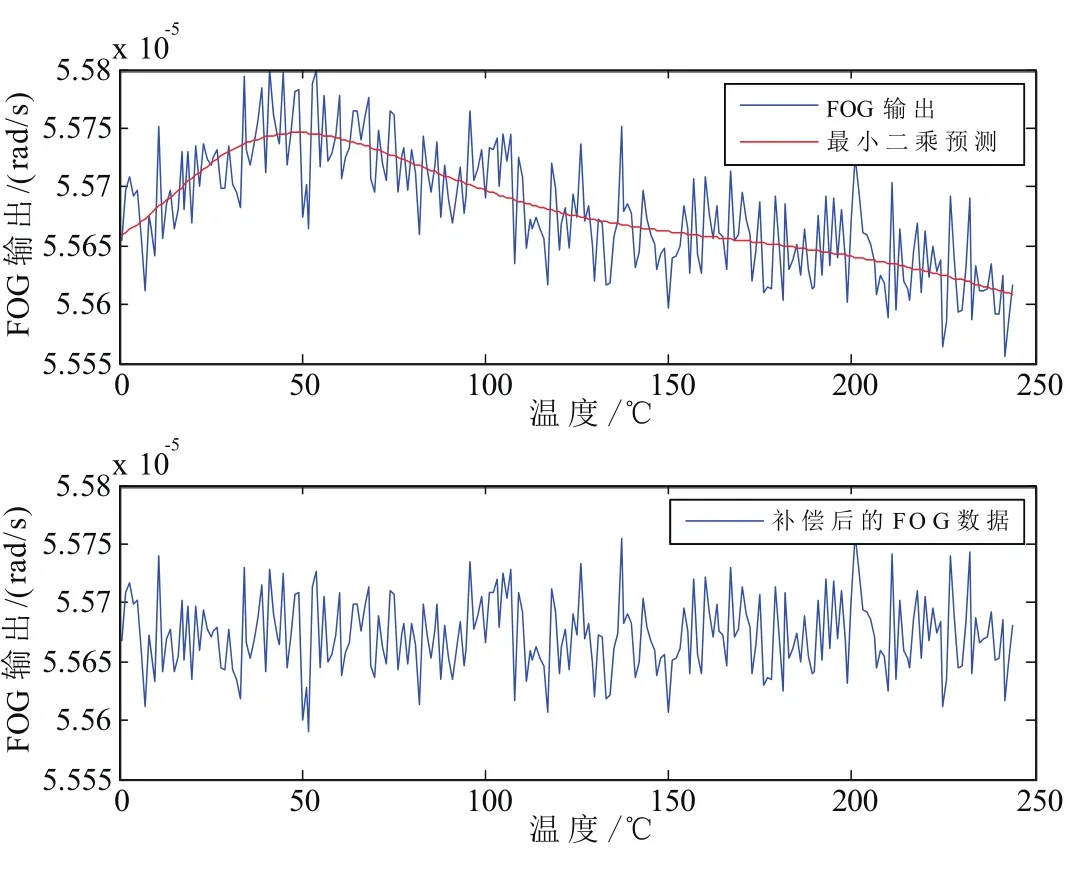
图5　最小二乘模型对预测数据的补偿Fig.5 Compensation by the least squares model

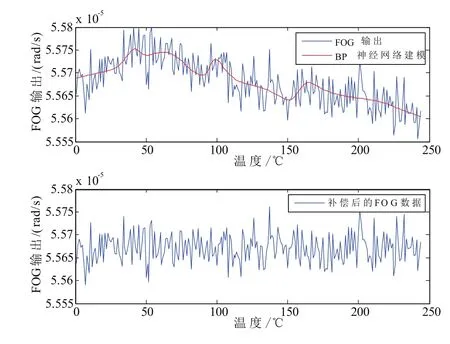
图6　BP神经网络模型对预测数据的补偿Fig.6 Compensation by BP neural network

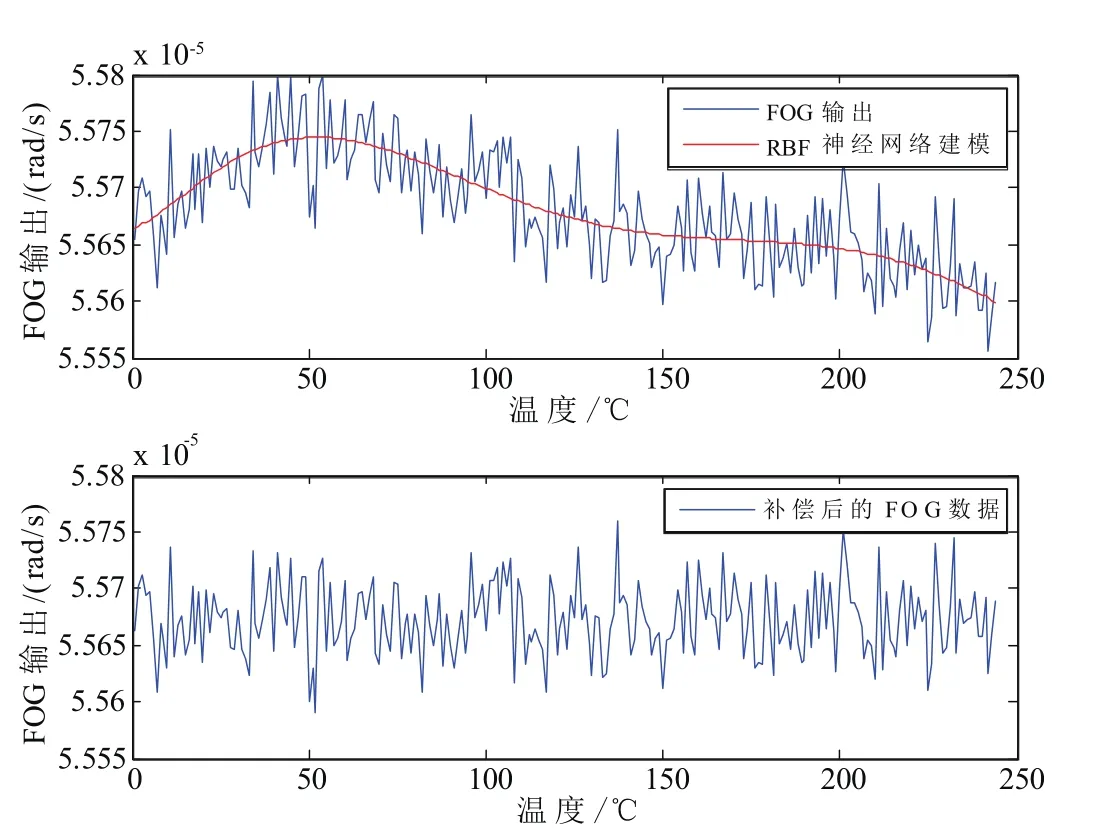
图7　RBF神经网络模型对预测数据的补偿Fig.7 Compensation by RBF neural network

图5～图7分别给出了使用三种误差模型对另一组测试数据进行温度漂移补偿的结果，补偿后的漂移误差对比如表1所示。

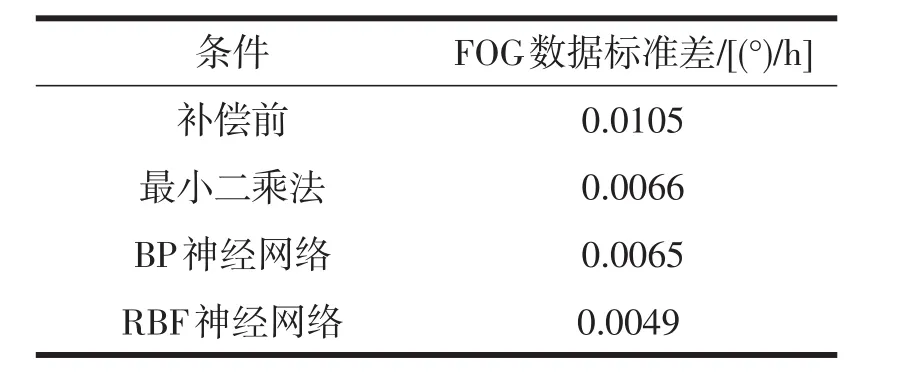
表1　三种建模方式补偿效果对比Tab.1 Compensation effect of three kinds of models

由表1可以看到三种补偿方案可以使FOG输出精度提高1倍。由于神经网络对非线性模型具有良好的拟合效果，使用BP、RBF神经网络对FOG温度漂移误差的补偿效果要明显优于最小二乘拟合。

6　结束语

光纤陀螺温度漂移是影响光纤陀螺输出精度的主要误差源之一，对光纤陀螺温度漂移误差进行有效的补偿可以在很大程度上提高光纤陀螺输出精度。本文为解决光纤陀螺温度漂移误差的拟合补偿问题，对基于最小二乘以及神经网络的三种拟合算法进行了研究，结合光纤陀螺温箱试验实测温漂数据对三种拟合算法进行对比，结果表明基于神经网络的非线性拟合模型对光纤陀螺的温漂误差具有较好的补偿效果。

参考文献

[1]Shupe D M.Thermally Induced Nonreciprocity in the FiberOpticInerferometer[J].Appl.Opt,1980,19(5): 654-655.

[2]杨孟兴,陈俊杰.光纤陀螺静态温度特性的分析及实验研究[J].中国惯性技术学报,2011,18(6):751-755.

[3]韩冰,林玉荣,邓正隆.光纤陀螺温度漂移误差的建模与补偿综述[J].中国惯性技术学报,2009,17(2):218-224.

[4]张岩岫,段红,祝建成.神经网络在光纤陀螺温度漂移中的应用[J].陕西科技大学学报,2008,26(05):95-98.

[5]周琪,秦永元,赵长山.光纤陀螺温度漂移误差的模糊补偿方案研究[J].传感技术学报,2010,23(07).

[6]刘鑫,乔彦峰.光纤陀螺随机漂移的建模与实时滤波方法[J].黑龙江大学自然科学学报,2013,30(01):129-134.

[7]李京书,许江宁,查峰,何泓洋.基于6类噪声项拟合模型的光纤陀螺噪声特性分析方法[J].兵工学报,2013,34 (07):835-839.

[8]赵曦晶,汪立新,何志昆,等.光纤陀螺温度漂移建模补偿[J].压电与声光,2013,35(04).

[9]任春华,潘英俊,解启瞻.捷联惯导系统中光纤陀螺温漂补偿研究[J].压电与声光,2009,31(04):472-476.

[10] 徐景硕,秦永元,顾冬晴.固定点平滑技术在惯导系统对准精度评估中的应用[J].测控技术,2004,23(11).

中图分类号：U666.1

文献标志码：A

文章编号：2095-8110（2014）03-0063-06

收稿日期：2014–08–28；

修订日期：2014–09–30。

基金项目：国家重大科学仪器开发专项（2011YQ0045002）

作者简介：张和杰（1965–），男，硕士，高级工程师，长期从事导航、制导与控制方向研究。E-mail:guoshiluo.love@163.com

Modeling and CompensationAlgorithm of FOG Temperature Drift with Neural Network

ZHANG He-jie1,GUO Shi-luo2
（1.Naval Department of Equipment,Beijing 100841,China; 2.College of Electrical and Information Engineering,Naval Univ.of Engineering,Wuhan 430033,China）

Abstract：FOG temperature drift is one of the major error sources that affect the FOG output precision,which is must be compensated in pratical application.Traditional least square method show low accuracy and poor aplicablity in the application of FOG temperature drift compensation.Modeling and compensation with BP or RBF neural network can improve the compensation accuracy effectively.Verifying and comparison the least square method with neural network compensation model,results show that this non-linear model based on neural network can improve the FOG temperature drift error compensation accuracy effectively.

Key words:FOG;Temperature drift compensation;Neural network;Non-linear model