自抗扰控制技术在电动舵系统中的应用

熊官送，那学智，曹东海

（北京自动化控制设备研究所，北京100074）

自抗扰控制技术在电动舵系统中的应用

熊官送，那学智，曹东海

（北京自动化控制设备研究所，北京100074）

摘要：针对无刷直流电机驱动的位置伺服系统，介绍了其自抗扰控制器设计的基本思路与实现过程。通过扩张状态观测器的动态补偿提高了电动舵机的鲁棒性，同时对系统闭环特性进行了分析，并对结果进行了仿真计算与实验研究，最后给出了自抗扰控制技术在快速响应电动舵机中的应用结果。

关键词：自抗扰控制器；无刷直流电机；舵机

0　引言

导弹精确制导技术的发展，特别是超音速导弹对舵机性能要求越来越高，如舵机应具有较大的功率输出能力、良好的低速跟踪性能、大负载下较小的跟踪误差等。传统电动伺服系统的控制回路从物理可实现的角度，基本上都是采用最经典的PID控制，使得控制性能的提升受到了一定限制。虽然目前已经有许多研究者从事现代先进控制算法应用于数字伺服系统的尝试，但是成功工程应用还是十分少见。造成这种现象的原因一方面是算法过于复杂，在控制器上难以实现，造成了控制算法的实用性不强。另一方面，数字伺服系统中存在着比较明显的死区、间隙、摩擦、饱和等非线性特性，使得其成为许多先进控制算法应用中的一个瓶颈因素。

自抗扰控制（Active Disturbances Rejection Control，ADRC）技术，是发扬PID控制技术的精髓并吸取现代控制理论成就，是从计算机仿真试验结果的归纳和综合中探索出来的，是不依赖于被控对象精确模型的、能够替代PID控制技术的新型实用数字控制技术[1]。自抗扰控制器主要由微分跟踪器、扩张状态观测器、非线性组合、扰动补偿等四个部分组合而成。其核心是扰动估计与动态补偿[2-4]。

本文针对舵系统中的扰动因素，特别是负载力矩，在建立舵机数学模型的基础上，设计了自抗扰控制器，提出了针对舵机控制对象特定问题的有效解决方案，并对引入ESO补偿后系统的回路特性进行了分析。实验结果表明，自抗扰控制器在不影响舵机响应速度的同时，具有提高伺服刚度、减小静差、增强抗负载扰动能力等优势。

1　舵机的数学模型

电动舵机一般由稀土永磁无刷直流电动机、传动机构和位置反馈传感器等组成。图1为目前广泛应用的电动舵机原理框图，将摩擦及外界负载扰动等效为扰动力矩Tl，传动机构简化为减速比i，忽略死区、间隙等非线性因素，其简化的运动方程见式（1）：

图1　舵机的结构框图Fig.1 Architecture of electromechanical actuation

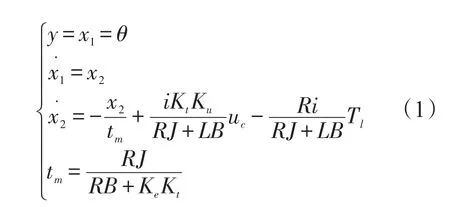
式中，θ为舵偏角，Uc为控制量，Ku为功率放大增益，i为传动减速比，R、L、Kt、Ke、B、J和tm分别为电机的电阻、电感、转矩系数、反电势系数、阻尼系数、等效转动惯量和机电时间常数。

2　控制器设计及分析

2.1舵机的LADRC控制器设计

ADRC的重要思想为采用状态观测器的方法对未知量进行观测和估计，并用于状态反馈和补偿，由式（1）可以看出，舵机模型涉及参数较多，且多数参数都是较小量值，在实际中很难精确测量，并且负载扰动Tl是未知量，通过设计合理的扩张状态观测器可以补偿未知扰动和未建模动态的影响。

从式（2）中可以看出，模型只与未知总扰动x3有关，令=w，得到状态方程：

可以将观测器设计为下面的形式[2]：

只要带宽ωo足够高，就可以将估计出的状态x3近似为z3，因此对于舵机模型式（2）可以等效为串行积分型，设计PD控制器为：

式中r为期望舵偏角，θ为实际舵偏角。由于对舵机的扰动进行了精确补偿，简单传统的PD控制就能满足要求，不考虑观测器的动态特性，则系统闭环传函为：

对于式（7）我们就可以方便地根据频域和时域指标去分析设计，通过使用线性ESO补偿可以避免使用积分补偿而导致的动态品质变差的缺陷。通过调整观测器的带宽，就可以对系统为建模动态和负载扰动进行估计，并进行动态补偿，因此可以实现高精度的控制。

2.2回路分析

自抗扰控制之所以具有很强的鲁棒性是由于建立在动态扰动实时估计并进行动态补偿的基础上，并且忽略了其观测误差。然而在实际应用中，扰动观测器带宽是受限制的，因此，需对有限带宽的自抗扰控制器进行闭环特性分析。由式（5）可得到式（8）。

代入式（6）得：

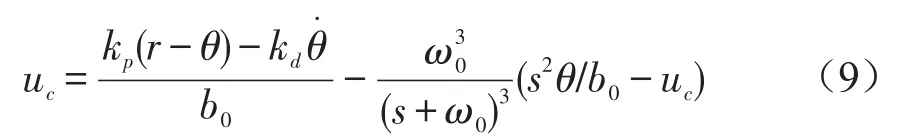
由式（9）可见，自抗扰控制器可等效为：在PD控制的基础上，增加了一项加速度滤波负反馈项和一个控制量滤波正反馈项，前三项与传统伺服系统采用的三回路位置、速度和电流控制基本相同，其等效回路框图见图2所示。图3为工程中常用的扰动观测补偿控制框图，通过对比图2与图3，不难发现其控制原理完全相同，线性ESO中的为被控对象的近似逆模型，而ω0同样为滤波器的带宽。但与扰动观测器不同的是，ESO（式（5））是通过积分形式实现了扰动观测和滤波，因此相对图3中的微分解算环节，ESO更适用于工程应用。

图2　自抗扰控制闭环等效回路Fig.2 The equivalent loop ofADRC

图3　扰动观测器补偿回路原理框图Fig.3 The scheme of disturbance observer

由于自抗扰控制器引入了扰动反馈回路，需要分析其对系统稳定性的影响。图4为某电动舵系统分别采用PD控制和自抗扰控制的系统开环Bode图，从图中可以看出，自抗扰控制器通过扰动观测补偿回路，将系统从原先的Ι型校正为ΙΙ型，同时增大了系统开环增益，且对高频段系统特性无影响，因此无积分器也可以实现对扰动的无静差控制，同时扩展了系统带宽（如图5）。但随着观测器带宽ω0的增大，系统的相角裕度随之下降，因此扩张观测器ω0的带宽不宜选择过高。

图4　开环Bode图Fig.4 Bode of open loop

图5　系统闭环频率响应Fig.5 Closed loop frequency response

3　仿真及实验

3.1仿真验证

通过设计（式（8））的控制律，在matlab下对系统进行了仿真，控制器主要参数为：kp=0.8，kd=0.035，b0=42330，w0=200，为了充分考虑系统抗负载扰动的能力，分别采用恒值负载力矩以及正弦负载力矩作用下，验证系统抗扰动能力，结果如图6及图7（力矩值为等效到电机轴上的力矩大小）。仿真结果说明，对于电动舵机在带载情况下，采用PD控制会带来较大静差，而采用ESO观测补偿扰动和PD控制的方法却能实现高精度控制，避免积分带来的迟滞、极限环等不利因素，是工程中理想的选择方案。

图6　恒值负载力矩下阶跃响应曲线Fig.6 Step response with±1N.m load

图7　正弦负载力矩下阶跃响应曲线Fig.7 Step response with sine load

从仿真结果可以看出，采用ESO补偿的自抗扰系统对常值及低频负载扰动有着很好的抑制作用，显著提高了系统的控制精度。但随着扰动频率的增加，抑制能力会越来越弱，这是由于受观测器的带宽所限，带宽越高对扰动的估计越精确，但同时对噪声也会越敏感，影响系统的稳定性。因此需要综合考虑噪声和扰动频率选择合理的观测器带宽。在一般情况下，通常将观测器带宽选择为系统闭环带宽3～5倍[5]。

3.2实验验证

将自抗扰技术应用于某型数字化无刷直流电动舵系统中，控制算法由数字控制器实现。在10N·m/(°)的弹性负载下进行测试验证，角度1V对应2°，舵机实测数据如下：

图8　阶跃信号响应曲线Fig.8 Loaded step response

图9　不同力矩负载下的响应曲线Fig.9 Step response with 10 N·m/deg load

采用PD控制时，系统阶跃响应调节时间为60ms，静差58mV，而采用ESO补偿后，调节时间为50ms，静差8mV；在10N·m/(°)的弹性负载下，采用PD控制时最大静差为400mV(0.8°)，而引入ESO补偿后，系统静差减小到50mV(0.1°)，如图9所示。测试结果表明，改进后的系统动态性能得到提高，解决了在大负载力矩下控制精度低的问题，取得了理想的控制效果。

4　结论

本文通过设计扩张状态观测器估计舵机的内外扰动，解决了传统的电动伺服系统抗负载扰动能力差的问题。与已有研究相比，本文对系统闭环特性进行了分析，发现电动伺服系统采用扩张状态观测器其基本原理与扰动观测器相同，前者通过积分形式估计扰动，在工程上应用性更强。通过仿真及实验验证，自抗扰控制技术可以提高数字电动伺服系统的控制精度和抗负载扰动的能力，相比PID控制具有更强的鲁棒性和更好的控制品质。

参考文献

[1]韩京清.自抗扰控制技术-估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008.

[2]高志强.自抗扰控制思想探究[J].控制理论与应用，2013.

[3]黄焕袍,万晖,韩京清.安排过渡过程是提高闭环系统“鲁棒性、适应性和稳定性”的一种有效方法[J].控制理论与应用,2001.

[4]孙明玮,焦纲领,杨瑞光,陈增强.自抗扰控制在飞行器控制与制导上的应用与分析－不同时间尺度问题的摸索[C].第29届中国控制会议.北京,中国,2010:6167-6172.

[5]Zhiqiang Gao.Art vs.Science in Control System Design [D].USA:Cleveland State University,2009.

中图分类号：TP273

文献标志码：A

文章编号：2095-8110（2014）03-0042-05

收稿日期：2013–03–18；

修订日期：2014–06–27。

作者简介：熊官送（1985–），男，工程师，主要从事伺服控制方面的研究。E-mail:xgs_ht0033@163.com

TheApplication of ADRC in ElectromechanicalActuation System

XIONG Guan-song，NAXue-zhi，CAO Dong-hai
（Beijing Institute ofAutomatic Control Equipment,Beijing 100074,China）

Abstract：Basic ideas of ADRC controller design process is introduced on the position servo system for brushless DC motor drivers.The electric servos robustness is improved by dynamic compensation of ESO,then the closed-loop system characteristics is analyzed,and the result is simulated and experimentally studied.Finally ADRC control technology in the rapid response to the application of the results of the electromechanical actuation is showed.

Key words:ADRC controller；BLDC；Electromechanical actuation