自主定向系统快速对准方法研究
孟乐中,何 英
(贵州航天控制技术有限公司,贵阳550009)
自主定向系统快速对准方法研究
孟乐中,何 英
(贵州航天控制技术有限公司,贵阳550009)
摘要:提出了一种基于动基座、大倾角的初始对准方法,研究了粗对准数学模型、罗经回路精对准数学模型以及捷联航姿解算数学模型,并实现样机设计。仿真结果和样机测试情况验证了该方法的快速性与精度,可为车载系统自主快速对准提供理论借鉴,具有一定工程应用价值。
关键词:自主定向系统;快速对准;仿真;试验
0 引言
初始对准从控制角度上讲就是施加一定的控制角速度把数学平台转向期望的位置(与地理坐标系重合),它是按误差方程进行控制的。自主初始对准技术是惯性技术的运用,在工程实现上具有一定的挑战性,并且现代战争对其测试精度、对准时间、使用环境以及工作可靠性等方面要求越来越严格,但由于与其它初始值测定方法相比具有较大优势,因此自主初始对准技术的研究已成为国内外惯性技术领域的研究重点。国内外在捷联惯导系统的初始对准方面已做了大量的工作。上世纪中叶,美国的Baziw和Leondes在研究主从传递对准方法时采用了卡尔曼滤波最优估计理论。80年代Porat和Bar-Itzhack针对发射车加速度对自主初始对准精度的影响进行了研究分析。90年代Goshen-Meskin和Bar-Itzhack从控制理论的角度出发,提出分段定常系统代替时变动态系统进行可观测性分析的PWCS理论,给动基座初始对准的可观测性分析提供了理论依据和分析。国内在对准方面也做了很多研究,北京航空航天大学研究了几种可观测性分析方法,并将这些方法应用于惯导初始对准的可观测性分析中,得出了一种更有效的确定不可观状态的方法,提出了一种新的自适应滤波方案。上海交通大学在舰载武器的初始对准时采用了参数不确定系统的鲁棒滤波方法,从产品测试精度得出鲁棒滤波的性能优于卡尔曼滤波的结论。此外,南京航空航天大学首次在惯性导航系统使用BP神经网络理论进行初始对准等研究。目前的国内外研究重点是在寻求显著提高对准精度同时缩短对准时间的手段,导出更有效的惯导系统误差模型及初始对准算法,以提高对准精度[1]。
自主定向系统安装在某武器系统发射架的末端,3min内完成自主对准并进入导航状态,对准后实时提供发射架的姿态角(即方位角、俯仰角和横滚角),并将发射架的姿态角传递给导弹,即完成了导弹的初始方位和姿态装订。自主定向系统成功研制对提高武器系统的机动性来说具有重要意义。它实现了武器系统停车就打甚至边打边走的可能性。
发射车在野外使用,自主定向系统使用环境比较严酷。自主定向系统在使用过程中会受到各种外界干扰如发射车发动机的震动、测试人员的走动、在野外阵风沙扰动(自主定向系统在不大于20m/s的阵风条件下能够正常工作)及发射车的机动等,这些干扰对自主定向系统对准产生影响,加大了自主定向系统的对准难度。根据自主定向系统使用环境,提出采用基于重力加速度作为参考矢量的解析粗对准算法和经典的罗经法精对准算法,并通过仿真和样机实施验证了算法的有效性。
1 自主定向系统对准技术模型
1.1基于重力加速度解析粗对准
1.1.1物理意义
基于重力加速度的解析式粗对准原理如下:在初始寻北计算过程中,选用惯性坐标系作为参考基准,同时将加速度计的输出值在参考坐标系中投影。当发射车处于静止状态时,在导航坐标系中发射车位置不会改变;但在惯性坐标系中,由于地球自转的原因,地球重力加速度会在以地球自转轴为主轴的锥面内发生缓慢的变化,变化情况如图1所示。因此,在不同时刻(间隔不为24小时的整数倍时)地球重力加速度在惯性坐标系内是不重合的。地球以恒定的角速度转动,当对准时间测量准确时,重力加速度在惯性空间内的方向改变包含了地球北向信息,而基于重力加速度解析粗对准正是利用了这一基本原理。
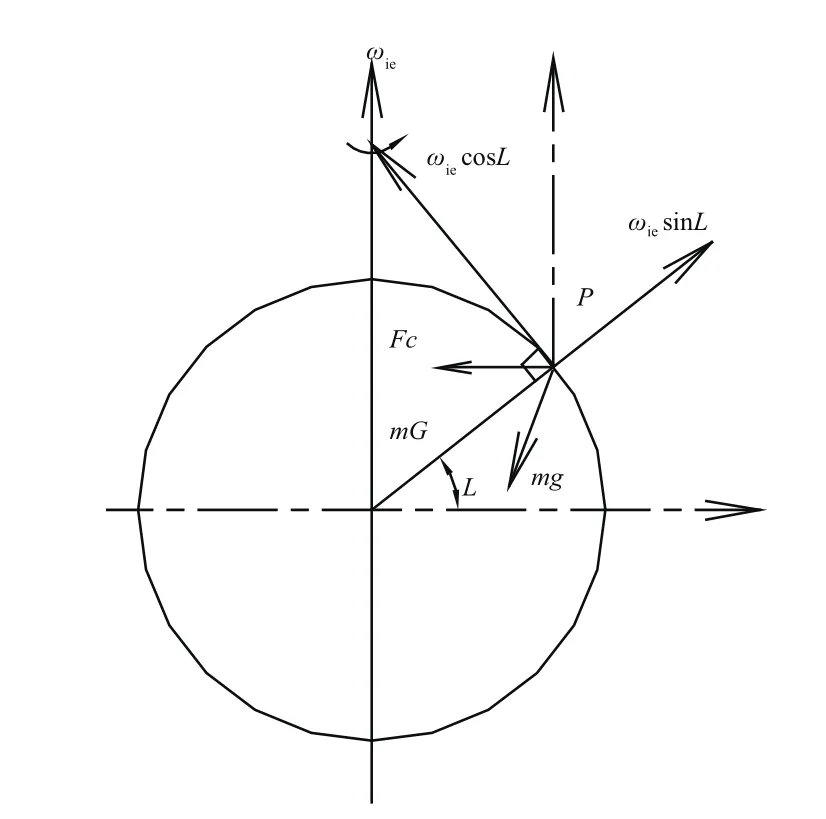
图1 惯性坐标系中地球重力加速度矢量Fig.1 Gravity acceleration vector of the Earth in an inertial coordinate system
1.1.2对准算法
坐标系的定义:①经线地球坐标系(oxe0ye0ze0),原点o在地球中心,ze0指向地球自转轴,xe0在赤道平面内并指向发射车在初始对准时刻所在位置的经线,ye0满足右手定则,该坐标系与地球固连,随地球转动;②经线地心惯性坐标系(oxi0yi0zi0),在初始对准时刻将oxe0ye0ze0在惯性空间凝固后所得到坐标;③惯性坐标系(oxi0yi0zi0ib0),它是在t0时刻将发射车坐标系b经惯性凝固后得到,其中t0为粗对准的起始时刻;④导航坐标系(oxnynzn),用于导航解算的参考坐标系,本文导航坐标系为东北天。通过转换得到发射车坐标到导航坐标的转换,表达式为:
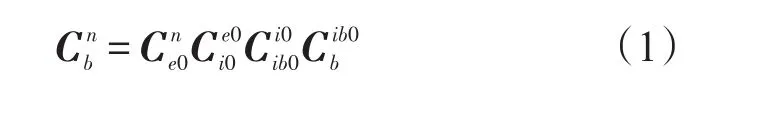
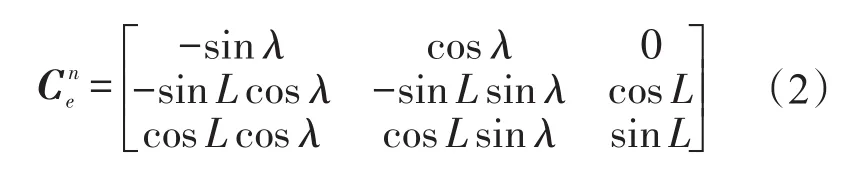
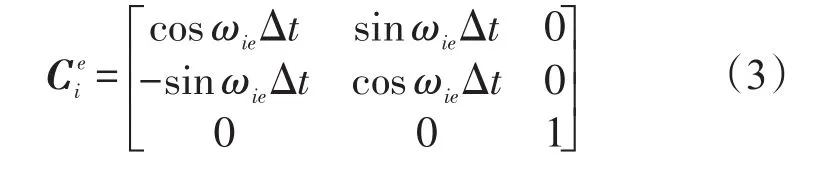
式中ωie为地球自转角速度,为载体坐标系b和惯性基座坐标系ib0之间的方向余弦矩阵,这个矩阵可以利用陀螺输出,通过四元数更新求解获得。递推更新计算的初始矩阵是单位矩阵I。

发射车在外部风扰的影响下,存在一定幅度摇摆和垂荡、纵荡、横荡运动。此时,加速度计的输出投影到惯性基座坐标系ib0为:

当载体受线性位移运动干扰时,例如风扰引起的垂荡、纵荡、横荡运动,可以近似为周期变化,在一段较长时间段内这种干扰加速度的积分值为零。在时间段t0到tk内,真实的速度值为:
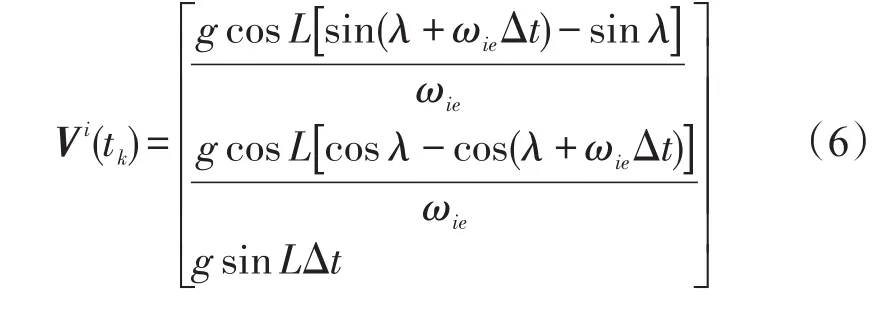
其中积分区间为Δt=tk-t0。
同时,对式(5)在时间段t0到tk内积分得到计算速度值为:
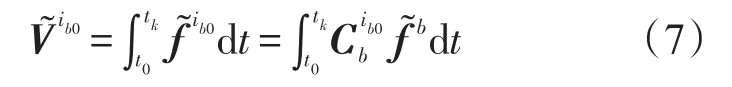
由真实的速度值与计算速度值可得:
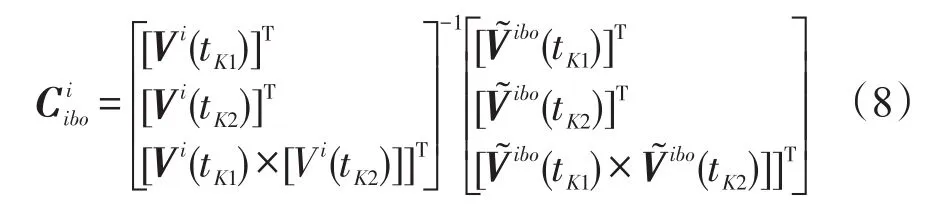
Vi可以通过式(6)计算得到,可以通过式(7)计算得到,再由式(8)可以计算出。通过式(2)和式(3)可以直接计算出和。利用四元数更新算法,可以递推计算出,最后将它们代入到式(1)中计算出捷联姿态矩阵。自主定向系统粗对准原理图如图2所示。
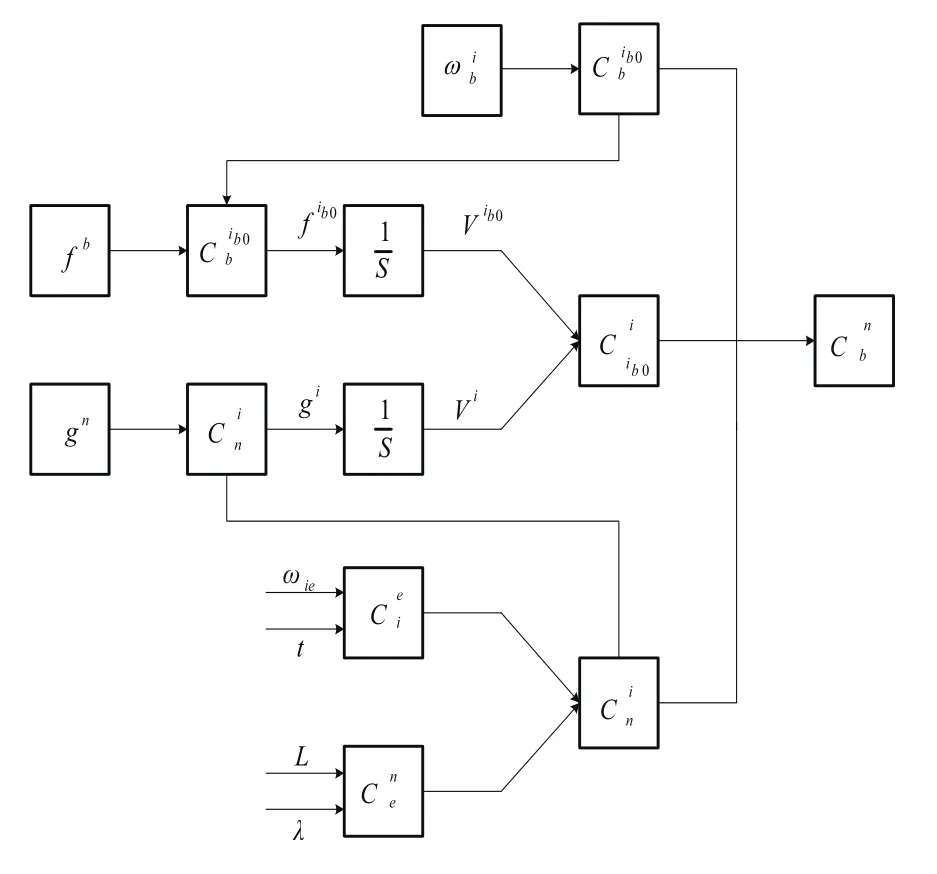
图2 自主定向系统粗对准原理图Fig.2 Coarse alignment schematic diagram of autonomous orientation system
1.2罗经回路精对准算法数学模型
罗经方位精对准是利用罗经效应寻北的原理来进行方位对准[2]。在水平对准的前提下,当平台坐标系的北向轴与真实北向存在误差角ϕz时,地球自转角速度Ω在地理北向投影为ΩcosL,在平台的东向也会出现投影,其值为ΩcosLsinφz。这个角速度引起俯仰误差角ϕx。当俯仰误差角的存在时,平台的水平方向上就会出现重力加速度g的投影,进而引起速度误差。这样就可以通过速度误差作为控制信号,来控制平台的航向误差角ϕz,使得ϕz减小到所需的范围内,即构成所谓罗经效应[3]。图3为应用罗经回路原理所设计的北向回路及罗经方位回路对准原理图。
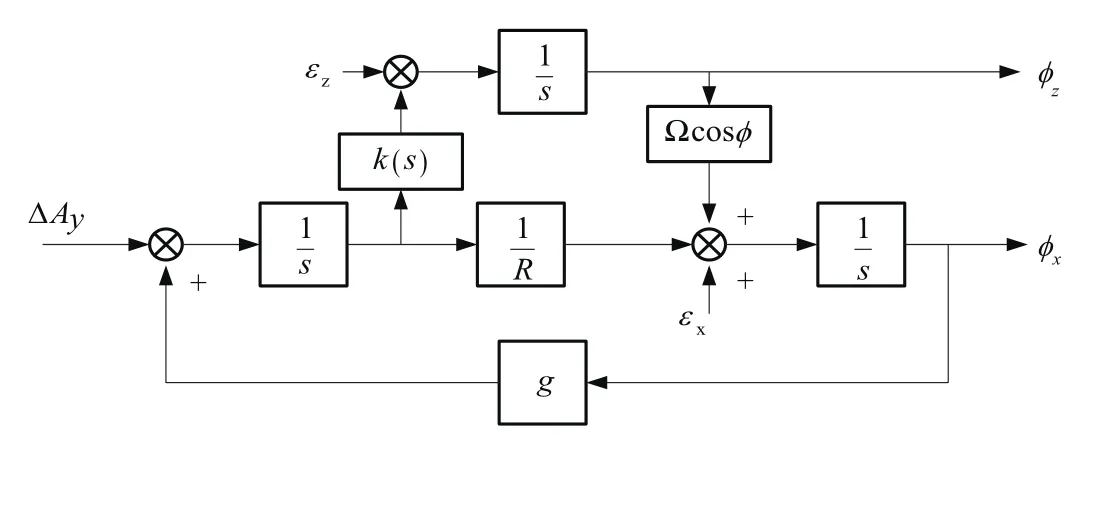
图3 罗经回路原理图Fig.3 Schematic diagram of compass loop
图中R为地球半径,εx、εy、εz表示等效的东向、北向和天向的陀螺漂移,ΔAx、ΔAy为等效东向和北向加速度计零偏,ϕx为平台俯仰误差角,ϕy为平台横滚误差角,ϕz为方位误差角。k(s)为速度控制环节。使用时针对系统的需要,合理的加入阻尼和增益,调整系统特性。
图4为东向水平回路设计原理图,图5为北向水平回路和方位回路原理图。
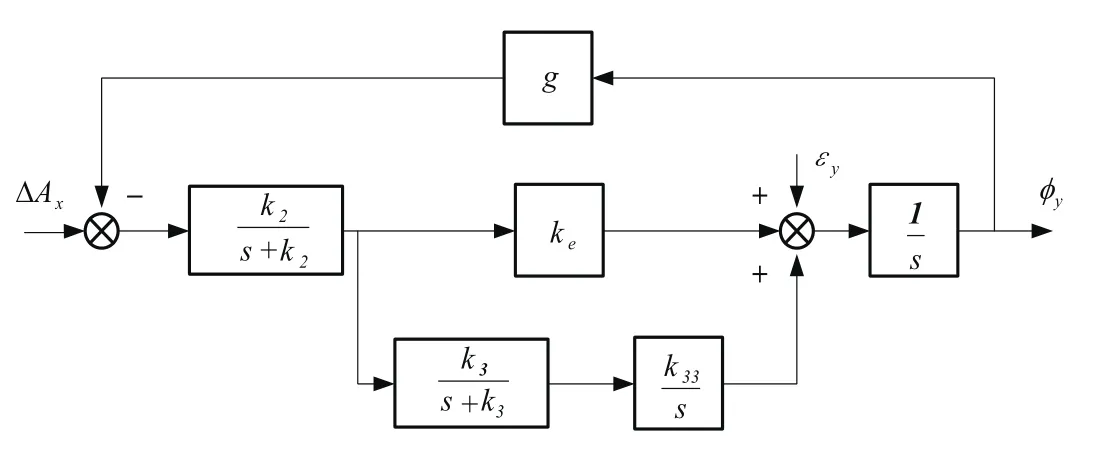
图4 东向水平回路原理图Fig.4 Schematic diagram of east loop
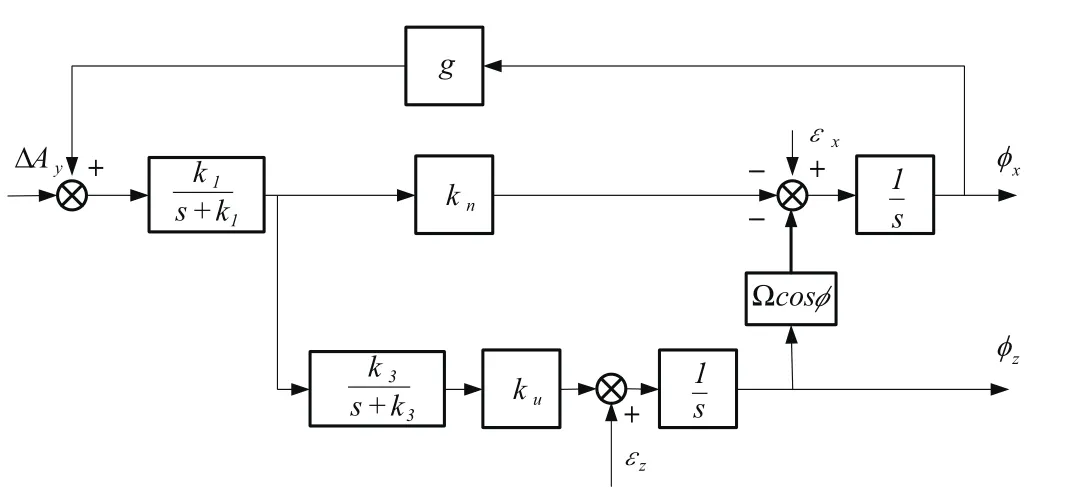
图5 北向水平回路原理图Fig.5 Schematic diagram of north loop
1.3姿态矩阵更新计算方法
在姿态解算过程中,由于刚体转动的不可交换性而产生的圆锥误差是不可避免的,为提高姿态解算精度必须采取相应措施减少误差。旋转矢量修正算法是克服圆锥误差的有效途径,本方法通常情况下使用陀螺测得的角增量信息来进行修正的;但目前国内使用的光纤陀螺输出信号为角速率,如通过角速率积分得到角增量再进行修正将会带来计算误差。为了减少计算误差,在姿态解算时直接利用角速率信号作为旋转矢量算法的修正信号。本方法以角速率作为算法的输入信号,用角速率表示旋转矢量的微分方程,以角速率的叉乘项拟合圆锥误差项,并且在典型圆锥环境中计算多项式的系数。基于角速率的圆锥误差补偿算法,应用于自主定向系统姿态矩阵的更新,有效得补偿了高动态环境下的圆锥误差,提高自主定向系统的姿态测量精度。
确定姿态更新周期H=tm-tm-1,H等于N倍的光纤陀螺采样周期h=tl-tl-1。利用光纤陀螺输出计算出发射车相对于惯性坐标系的角速度计算旋转矢量增量Δϕ。其具体步骤为:
由光纤陀螺输出的输出计算Δϕ中的惯性可测项,即角增量α。每个姿态更新周期H内已知N+1个光纤陀螺采样角速度ω0、ω1、...ωn;则姿态更新周期H内的角增量α为:

式中:
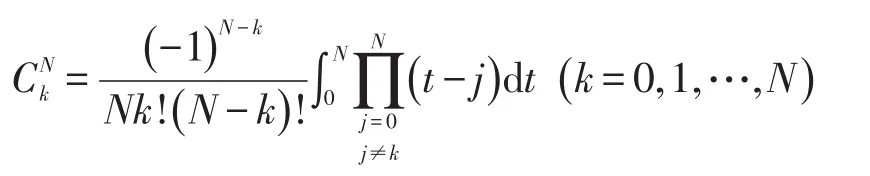
由光纤陀螺输出的输出计算Δϕ中的非惯性可测项,即圆锥补偿项β;每个姿态更新周期H内已知N+1个光纤陀螺采样角速度ω0、ω1、...ωn。
在姿态更新周期H内,圆锥补偿项β由光纤陀螺采样角速度叉乘项的线性组合来计算。
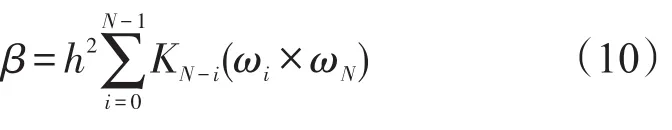
式中KN-i为优化系数,在典型圆锥环境中确定。
得到的姿态更新周期H内角增量α,与姿态更新周期H内圆锥补偿项β相加,得到姿态更新周期H内旋转矢量增量Δϕ。

设置N=3,陀螺在t时刻采样角速度ω0,并且每个姿态更新周期H,在t+H/3、t+2H/3、t+H时刻采样ω1、ω2、ω3;得到姿态更新周期H内旋转矢量增量Δφ为:
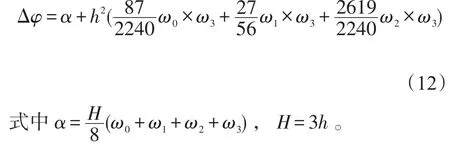
以上是基于角速度计算旋转矢量增量的过程。
计算得到旋转矢量的增量Δφ后,通过旋转矢量与四元数的关系,得到姿态更新周期H内姿态更新四元数q(H)。
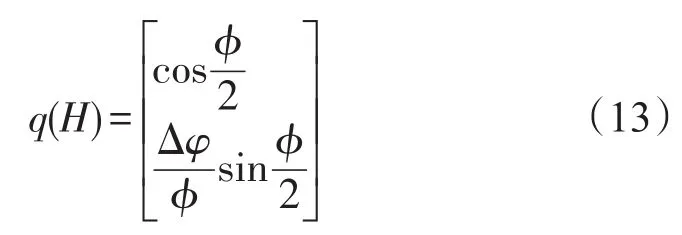
由姿态四元数更新方程更新姿态四元数。

式中Q(tm)、Q(tm-1)分别表示载体在tm、tm-1时刻的姿态四元数。
以光纤陀螺的角速度作为算法的输入时,直接利用角速度计算旋转矢量,计算四元数,避免了常规算法角速度到角增量的积分误差,其性能优于传统算法。
2 算法仿真分析
2.1仿真环境设置
为了验证本方法的可行性,利用仿真软件进行仿真,仿真条件如下:
1)地理位置:纬度L=26.5°、经度λ=106.5°,高度h=1070m;
2)陀螺常值漂移0.02(°)/h、随机游走误差0.01(°)h12;加速度计常值偏置1×10-4g;
3)基座晃动条件:在自主定向系统三个方向上加入频率 f=1Hz,幅值A=3°的角振动;
4)姿态初始值:俯仰角为55°、横滚角为0°,方位角0°。
仿真时间180s,其中,前30s进行粗对准,粗对准结束后,再转入进行精对准。各姿态误差角如图6所示。
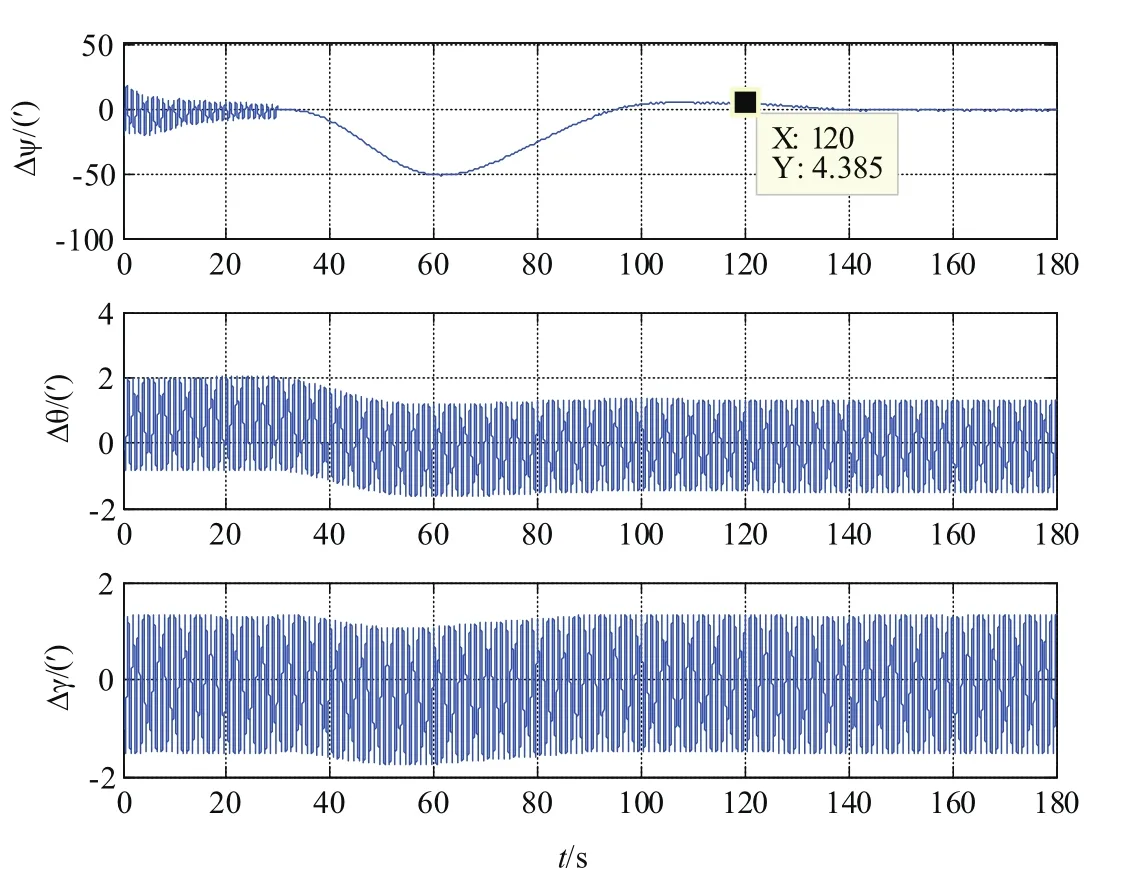
图6 三轴摇摆时180s对准误差Fig.6 Alignment error over 180 seconds upon three axes swaying
由仿真分析可知,对于姿态调平,罗经对准法具有较高的抗外界扰动能力,能够在短时间内收敛至较高精度,在仿真时间60s后,东向误差角和北向误差角稳定在一定范围之内,最大跳动量在0.05°以内。因此,罗经姿态调平在工程中被广泛应用。
对于方位对准,抗外界扰动效果较差,在进入罗经方位对准时有一定的超调,但在120s时,航向误差收敛到0.1°以内。在180s时,航向误差收敛到0.05°以内。
3 试验验证
在完成了自主定向系统的方案论证和理论研究后公司开展了原理样机研制工作。2014年3月在公司惯导试验室对样机进行性能测试:样机测试测试条件为俯仰角初值为55°、横滚角初值为0°、每隔60°进行一次对准,同时在航向和俯仰方向施加频率 f=1Hz,幅值A=3°的角振动。测试数据见表1。
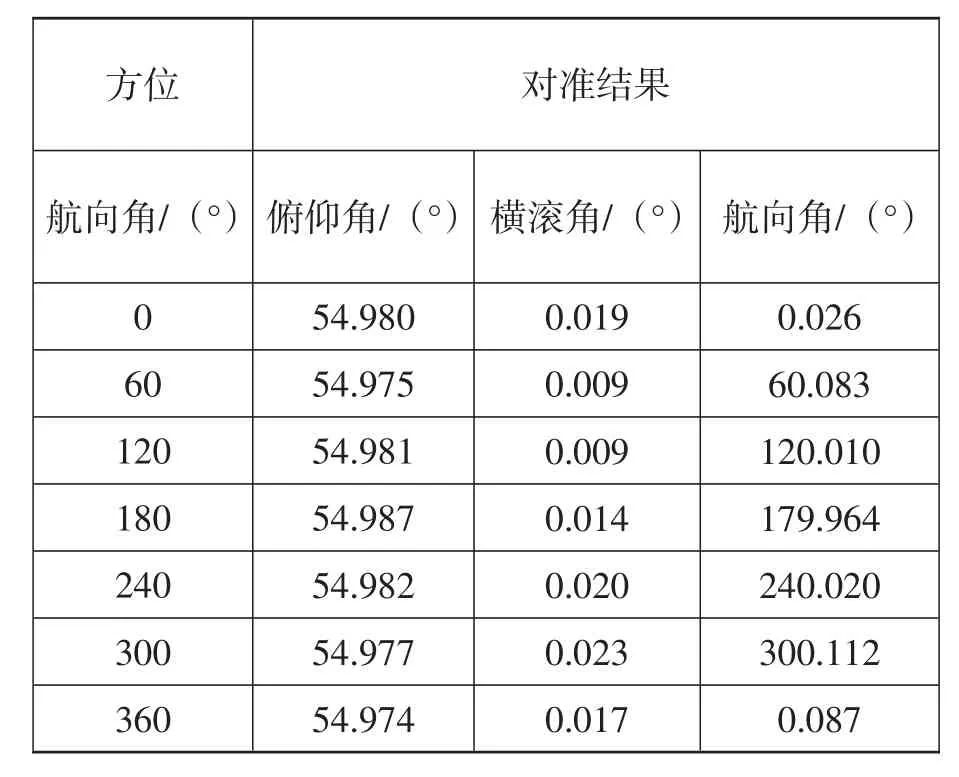
表1 测试结果Tab.1 Results of the test
从表中测试的数据可以得出,在上述的条件下,在3min内航向角最大误差为0.112°、俯仰角最大误差为0.02°、横滚角最大误差为0.023°,优于发射车的指标要求。
4 结论
本文首先对自主定向系统可能受到的干扰进行深入的分析,建立了新的动基座对准方法和姿态更新方法,该方法能够完全不依赖任何外部信息自主实现了动基座初始对准功能。
仿真结果和样机测试情况表明,该方案切实可行。利用光纤陀螺进行发射车的初始姿态测试在国内属于首创,而且对准条件恶劣:要求在阵风等干扰条件下、俯仰角为55°、3min完成对准,该自主定向系统成功研制在惯性领域中是一项技术突破。
参考文献
[1]聂莉娟.捷联惯导系统初始对准滤波技术研究[D].工学硕士学位论文,哈尔滨工程大学,2004,1.
[2]王进,练军想,吴美平.捷联惯导系统初始对准方法比较[J].国防科技大学机电工程与自动化学院.
[3]秦永元.惯性导航[M].北京:科学出版社.
中图分类号:TP273
文献标志码:A
文章编号:2095-8110(2014)03-0031-06
收稿日期:2014–05–16;
修订日期:2014–09–27。
作者简介:孟乐中(1975–),男,硕士,主要从事惯性导航技术方面研究。
Research on RapidAlignment Method forAutonomous Orientation System
MENG Le-zhong,HE Ying
(GuizhouAerospace Control Technology Ltd.,Guiyang 550009,China)
Abstract:The initial alignment method is proposed based on moving base and large inclination.It makes a study on the mathematical models of coarse alignment,compass loop fine alignment and strap-down attitude determination.And the prototype design is realized.The rapidity and accuracy of the proposed method is proven by simulation results and prototype tests.This provides a theoretical basis for the autonomous rapid alignment of the vehicle-mounted system and has a certain engineering value.
Key words:Autonomous orientation system;Rapid alignment Simulation;Test

