FSAE赛车车架结构拓扑优化及轻量化设计研究

郑文杰++兰凤崇++陈吉清

摘 要：采用拓扑优化的方法对FSAE（Formula SAE）赛车车架结构进行优化改进。经过拓扑优化后车架的结构更加简洁，改进后车架的前后舱管件减少，质量降低，前环由倾斜改为垂直设计，降低了加工难度。采用尺寸优化对车架进行轻量化设计研究。经过尺寸优化后，得到了不同部位钢管的壁厚参数，实现车架减重13%的轻量化目标。对车架性能进行仿真分析，验证了车架强度满足使用要求，同时车架的弯曲刚度和一阶模态频率都比原车架有所提高，保证了FSAE赛车车架结构的性能和轻量化。

关键词：FSAE赛车；车架；拓扑优化；尺寸优化；轻量化设计

中图分类号：U462.1文献标文献标识码：A文献标DOI：10.3969/j.issn.2095-1469.2016.01.06

Abstract：The topology optimization method was used to optimize the frame structure of FSAE racing car. Results show that after optimization the structure is more compact and the frame weight is reduced due to the removed tubes on the front and rear tank. The front ring is changed from inclined to vertical， which allows for easier processing. After size optimization for lightweight design， the frame weight is reduced by 13% and the tube thicknesses in different locations were obtained. The simulation analysis was carried out for the frame to verify that the strength meets the requirements. Meanwhile the bending stiffness and the first order modal frequency are also improved so that both the performance and lightweight of FSAE car are ensured.

Keywords：FSAE car； frame； topology optimization； size optimization； lightweight design

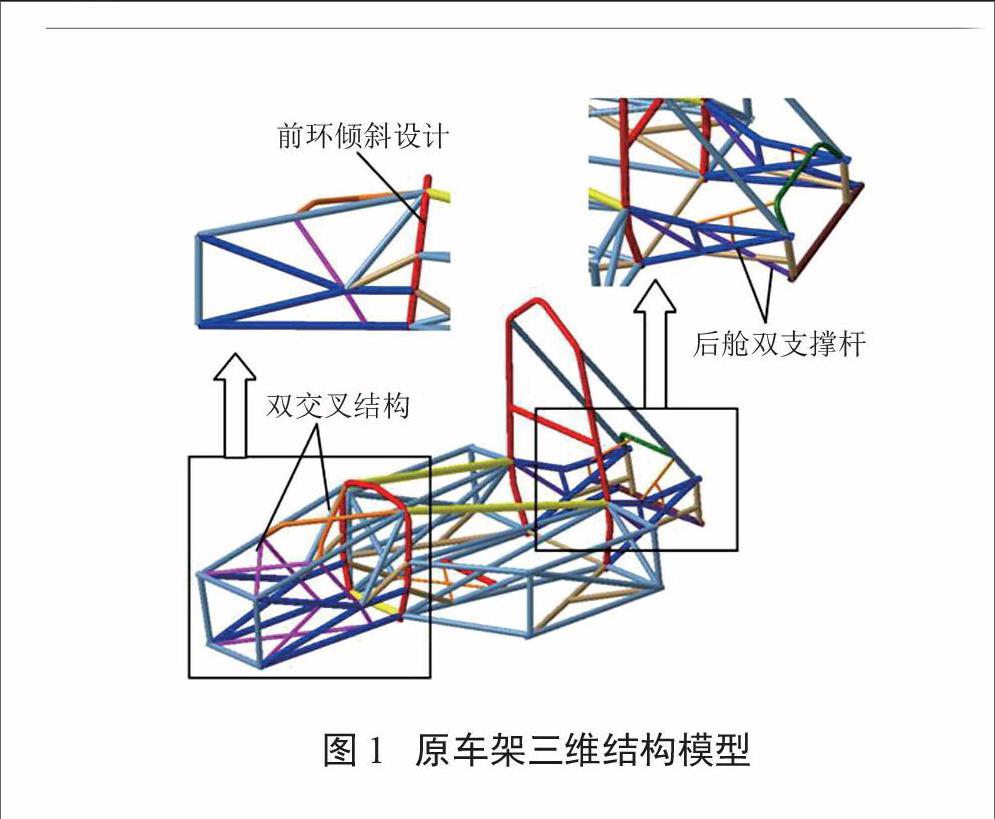
近年来，轻量化已经成为汽车工业重点关注的发展方向之一[1]，也是赛车设计研究的热点。随着FSAE赛车竞技水平的不断提高，对赛车的设计要求也越来越高。车架作为赛车的装配基体，是整车设计的一个重要环节，其性能高低将直接影响整车性能和比赛成绩。第一辆FSAE电动赛车在2014年获得全国第二名的好成绩，但是由于设计周期短，经验不足，车架结构仍有许多问题需要改进。图1为原赛车车架结构的三维模型。分析发现，原车架是以高刚度作为设计目标，因此，在车架的前舱和后舱均采用了双交叉结构形式以尽可能提高车架的扭转刚度，但是这也直接导致了车架的结构复杂，重量增加。有研究表明，赛车重量每减少5 kg，完成一圈赛道的成绩可以提高12 s[2]。由于电动赛车所用电池的能量密度小，并且FSC比赛规则中严格规定了电动赛车的动力电池最大功率不能超过85 kW[3]，所以车架轻量化成为提高电动赛车的动力性、操纵稳定性和比赛成绩的关键技术。除了结构复杂以及轻量化问题突出之外，原车架设计与人机工程设计匹配不佳，在设计车架前环时采用了倾斜的设计形式，这不仅增加了焊接加工难度，也增加了制造成本。基于原车架存在的上述问题，本文采用了拓扑优化和尺寸优化的方法对车架进行优化改进，其优化设计过程如图2所示。

拓扑优化是一种创新性的设计方法，能为设计者提供一些新颖的拓扑结构[4]。拓扑优化的结果将决定产品的最终形状和性能[5]，因此拓扑优化在复杂结构的造型和轻量化设计中具有非常重要的价值[6]。

中北大学的王振刚采用拓扑优化设计了燃油赛车新的车架结构形式，并且使车架减重了21.7%[7]，同时保证了赛车的强度、刚度等性能不降低。拓扑优化是在产品概念设计阶段寻找最优材料布局，使结构更加合理，材料利用率更高，从而实现轻量化[8]，可以为赛车车架的结构改进提供新的设计思路。

尺寸优化是详细设计阶段为设计者提供具体优化参数的一种方法。它常用于管、梁等带有截面属性的参数优化[5]，也是钢管桁架式车架轻量化的重要手段。南京农业大学的王兵等通过对车架的模态灵敏度分析，对FSAE赛车车架进行了尺寸优化，改进了车架的强度富余部位，使车架的质量下降了5.67 kg[9]。基于上述研究经验，采用拓扑优化和尺寸优化的设计方法，对原来的电动赛车车架进行优化改进。改进后车架的结构更加简洁合理，弯曲刚度和第一阶模态频率都比原来有所提高，并且使车架减重了13%，实现了轻量化，提升了赛车的整车性能。

1 车架的拓扑优化

1.1 建立拓扑优化模型

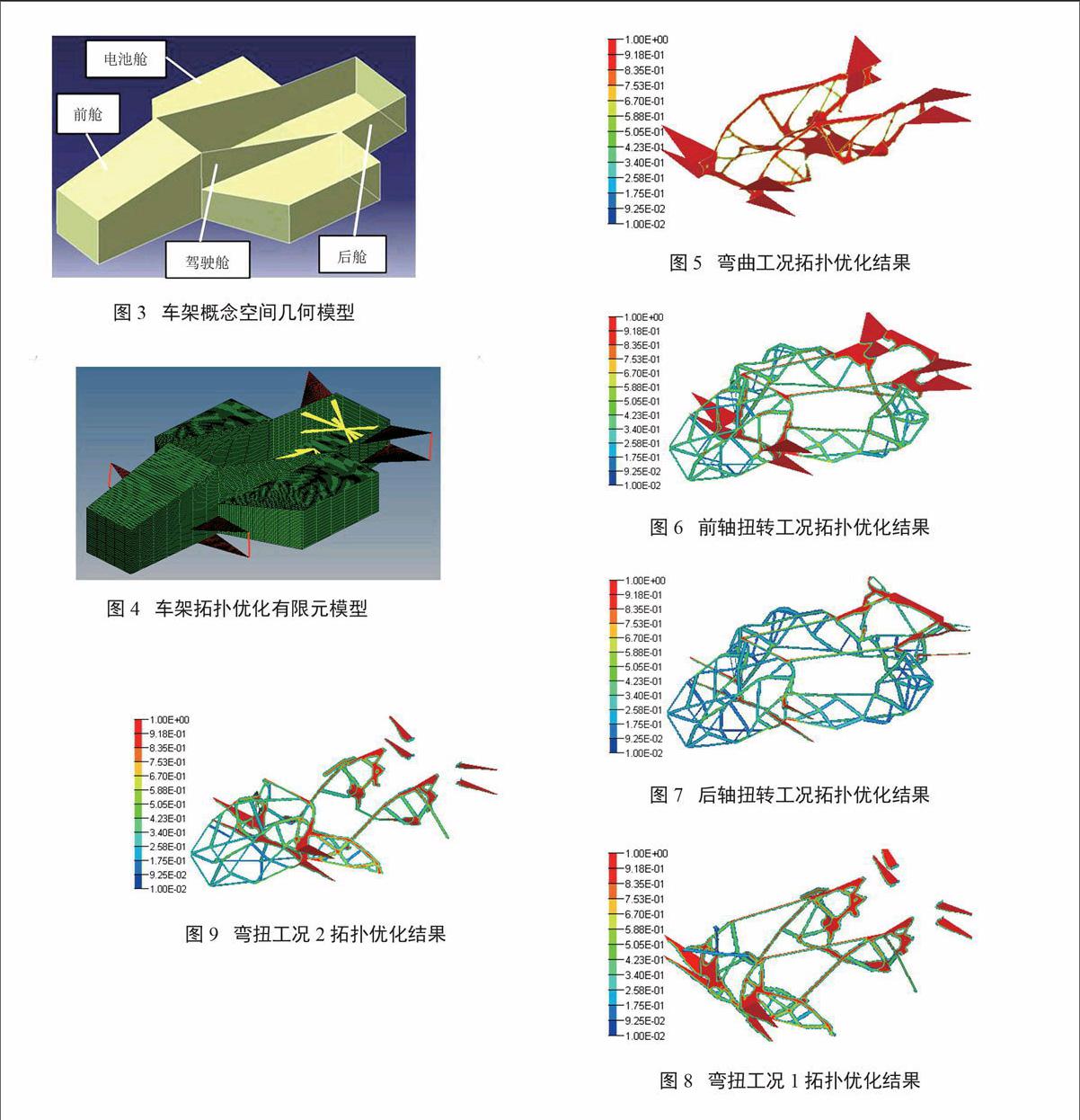
车架的拓扑优化模型包括概念空间几何模型和有限元模型。概念空间的几何模型严格按照FSC赛事规则要求进行建立。比赛规则中对于车架各个不同部位的空间尺寸大小都有严格的规定，包括对于驾驶舱内部横截面、驾驶舱开口形状及尺寸、主环和前环斜撑件的倾斜角度等尺寸参数都有相关的建模规范。几何模型是进行数值模拟的基础[9]，为了权衡计算效率和计算精度，对拓扑优化几何模型进行了简化。为了得到最优的拓扑结构，建立几何模型时省略主环和主环斜撑等在车架主要承载工况下传力影响不大的构件。对于后舱与电机、电池连接部分，前舱与悬架硬点连接部位等细节也作相应的简化处理。另外座舱的纵向尺寸、横向尺寸以及前环转向盘安装位置的高度尺寸由人机工程的要求决定。建立车架的概念空间几何模型如图3所示。

在有限元建模中，对于前舱、驾驶舱以及后舱等平面舱壁结构以二维的壳单元表示。悬架是采用双横臂独立悬架形式，在模型中以平面三角板的形式进行模拟，是以壳单元进行有限元网格划分，但是悬架部分设定为拓扑优化的非设计区域。车轮与悬架相连部分的立柱以刚性rigid单元来模拟。另外车架上电池、电机、座椅等都是通过螺栓与车架相连，这些部分也是通过刚性单元来处理，主节点位于相应集中质量的质心位置，从节点则与螺栓连接部位重合，集中力直接施加在对应的主节点上。拓扑优化有限元模型如图4所示，模型的单元总数为56 067个，其中四边形单元55 603个，三角形单元464个。

1.2 拓扑优化结果分析

拓扑优化选择了纯弯曲工况、前轴扭转工况、后轴扭转工况和两种不同比例的弯扭工况一共五种典型工况进行优化计算。同时控制模型的最大成型尺寸和最小成型尺寸以避免材料堆积和消除细小的传力路径。前三种工况优化目标为结构柔度最小，后两种工况则以结构的加权柔度最小作为优化目标进行迭代。上述五种工况下的拓扑优化结果分别如图5～9所示。

图5所示为纯弯曲工况下拓扑优化结果，车架材料集中分布在座舱两侧，前后舱没有出现材料分布。图6和图7分别是前轴扭转和后轴扭转工况下的拓扑优化结果，除了座舱底部之外，车架的其它部位都出现了比较清晰的材料分布路径，车架的轮廓基本形成。图8和图9分别表示纯弯曲工况、前轴扭转工况、后轴扭转工况三种子工况在2∶1∶1和1∶2∶2权重因子下弯扭联合工况的拓扑优化结果。根据图8所示，弯扭工况1由于弯曲工况权重是扭转工况的两倍，导致车架材料分布只出现在座舱周围，与纯弯曲工况结果较为相似，另外电池舱前端也出现了小部分材料分布。当增加扭转工况的权重之后，车架的材料分布则相对平均，如图9所示，在座舱和前舱以及电池舱等部位都出现了材料分布。

1.3 提取拓扑结果与车架建模

根据以上五种工况的拓扑优化结果，通过转换成CAD数据导入三维建模软件CATIA中进行车架的几何建模，并重点处理车架前舱和后舱的结构。

分析以上五种拓扑优化的结果可以发现，在车架的前舱和后舱都出现较为复杂的交叉状材料分布，这将会极大提高车架的扭转刚度。为了减轻车架重量需要牺牲一定的刚度。将前舱顶部双交叉结构改为单交叉结构，后舱的双支撑杆改为单支撑杆，以减少管件，简化车架结构。改进后的车架三维结构模型如图10所示。

对比图2和图10可以看出，前舱的交叉管件更少，前舱顶部由原来的双交叉结构改为单交叉结构，前环斜撑减少两根钢管。前环结合人机工程要求，由原来的倾斜设计改为垂直设计形式，有利于降低加工难度。后舱则取消了原来多余的高压电缆保护钢管，并且考虑到后舱在安装电机存在强度剩余的情况下，将原双支撑杆结构改为单支撑杆形式。对比原车架结构可以发现，根据拓扑优化结果建立的新车架更加简洁，钢管用料更省，在相同钢管尺寸情况下质量更轻。

2 车架的尺寸优化

2.1 尺寸优化建模与优化设置

在车架结构造型确定的情况下，尺寸优化能进一步优化车架钢管参数，可以改进车架的剩余强度。车架有限元模型以壳单元表示，平均尺寸为10 mm，单元总数164 919个，四边形单元156 749个，三角形单元8 170个，车架材料是30CrMo钢材。由于大赛规则对于车架不同部位的钢管壁厚有不同尺寸的范围要求，为了满足赛规要求，在模型中设定管件的外径，以壁厚作为设计变量，令壁厚尺寸沿内径方向连续变化。此外根据赛规要求将车架不同部位的钢管分为6组外径尺寸类型，同组及对称管件设置相同属性，以保证优化结果的可行性，同时又可以减少设计变量提高计算效率。最终设计变量为6组钢管壁厚，初始设计壁厚均设置为3 mm，最小壁厚设置为0.5 mm，设计变量连续可变，优化目标为结构质量最小，约束材料的最大应力不超过785 MPa，控制悬架硬点的最大变形量在合理范围内，约束优化后整体质量不低于30 kg，以保证优化结果的收敛。

2.2 尺寸优化结果分析

尺寸优化的结果如图11所示，不同颜色表示壁厚尺寸不同的钢管。为满足规则及实际加工要求对优化后的尺寸进行圆整处理，最终车架的钢管壁厚参数见表1。经过优化后，车架的前舱顶部交叉钢管壁厚由原来的1 mm减少到0.8 mm，前环斜撑和后舱管件壁厚由原来的1.6 mm分别减少为1.4 mm和1.5 mm。最终优化后的车架设计质量为37.4 kg，实际加工出来的车架重为39.6 kg，比原车架的45.8 kg降低了6.2 kg，减重比例达到13.5%，轻量化效果明显。

3 车架结构性能的仿真分析

3.1 车架的刚度性能分析

刚度表示车架抵抗变形的能力。刚度太低会导致车架在受力时变形过大，影响整车的操纵稳定性和安全性，刚度过高容易增加车架质量。一般而言，车架的弯曲刚度越大越好[10]，而扭转刚度与赛车的悬架刚度有关，一般取为悬架刚度的5～10倍为宜[11]。在车架的扭转刚度分析模型中，约束两后轮轮心全部6个方向自由度，释放两前轮所有自由度，并在两前轮轮心处施加大小为1 000 N·m扭转力矩，模拟车架的扭转变形工况。在弯曲刚度分析模型中，约束四个车轮的全部6个自由度，在座椅安装杆与驾驶舱两侧最底部的侧边防撞杆连接处分别施加大小为1 000 N的垂直力，模拟车架在垂直载荷作用下的弯曲变形工况。

图12为车架扭转变形位移云图，两对称力作用点位移分别为±3.88 mm，经计算车架的扭转刚度为2 876 N·m/（°），比原来的3 400 N·m/（°）略有下降，这是车架结构简化，管件减少所致，仍然满足设计要求。图13为车架弯曲变形位移云图。图14为对应的车架挠度曲线，最大挠度值为-0.54 mm，经计算得到弯曲刚度为3 676 N/mm，比原车架的弯曲刚度1 753 N/mm提高2.1倍，说明车架抵抗弯曲变形能力更强。刚度分析表明，车架的扭转刚度和弯曲刚度都比较高，在满足使用要求的同时实现了轻量化目标。

3.2 车架的强度性能分析

强度是对电动赛车的最基本性能要求。车架不仅要具备良好的刚度性能，还要满足强度的要求，以确保在比赛过程中车架钢管结构不被破坏，以防发生安全事故。选择了最大制动力制动和最大侧向加速度转弯两种极限工况对车架进行强度校核，其仿真结果如图15～18所示。

由图15可知，当赛车以最大的制动力（最大制动减速度为-15.68 m/s2）进行制动时，车架上的电机和电池等集中质量将产生一个纵向惯性力，导致车架上集中质量安装部位发生了相应的位移，最大位移出现在座椅和安全带安装杆连接处，位移大小为0.376 mm，车架其余大部分位置的位移都在0.251 mm以内，说明车架的整体变形很小。由图16制动工况应力云图可知，最大制动力制动工况下车架的最大应力出现在座椅安装点，应力大小为85 MPa，远小于30CrMo的屈服强度785 MPa，即使考虑焊接导致钢管强度下降，车架的强度也满足要求。

图17是赛车向左极速转弯工况下（最大侧向加速度为16.66 m/s2）的位移云图，可见车架有整体向右侧翻的趋势，右侧电池舱和主环部分位移较为明显，最大位移出现在座椅安装点为0.311 mm处。由图18转弯工况应力云图可知，该工况下车架的应力分布主要在集中质量与车架接连处，与制动工况类似。由于最大侧向加速度比最大制动减速度大，所以转弯工况下最大应力比制动工况下的最大应力值高很多，达到160 MPa，出现在座椅安装点位置。经校核，该工况下的应力值仍然小于安全极限值，车架的强度满足要求。

3.3 车架的模态性能分析

车架的静态刚度主要通过扭转刚度和弯曲刚度两个指标来评价，而动态刚度的主要衡量指标则是模态频率。车架结构的低阶弹性模态，不仅反映了车架的整体刚度性能[12]，同时也是控制赛车常规振动特性的重要指标。车架模态频率要错开路面激励，以防止共振对车架以及整车结构造成破坏性影响。对车架的前6阶模态性能进行计算分析，其分析结果如图19和表2所示。

由图19可知，车架在不同频率下发生了不同的振动变形。表2为优化前后车架的前6阶频率变化，可以看出优化后除了第6阶频率外，车架的前5阶频率均比优化前提高，其中第一阶模态频率达到了68.4 Hz，比优化前提高了19%。赛车比赛速度较高，对于动态性能要求更高，所以更高的频率对于赛车更加安全。路面是汽车振动的基本输入，路面激励频率范围约为0.5～25 Hz[13]。从车架的模态分析结果来看，车架的低阶固有频率都比较高，其中第一阶固有频率远高于路面激励的共振频率范围。此外，由于电动赛车的电机在加速、减速过程中都处在一个无级变速的过程，所以电动赛车不存在所谓的怠速振动问题。由模态分析可知，无论是对于实际的比赛场地路面，还是对于电机振动而言，改进后的电动赛车车架动态频率都满足安全的要求。

经验证，改进后车架的各项性能均满足设计要求，并成功应用到新赛车的实际制造，图20为改进后实际加工制造出来的新赛车车架实物。

4 结论

本文采用拓扑优化法和尺寸优化方法对电动赛车原车架进行优化改进设计，得出以下结论：

（1）经拓扑优化后，车架前后舱结构比原车架更 加简洁，管件更省，有利于轻量化。前环由倾斜改为垂直设计，降低了加工难度。

（2）通过尺寸优化，使改进后车架的钢管壁厚比原来减小，车架的重量由45.8 kg下降到39.6 kg，减重幅度达到13.5%，轻量化效果明显。

（3）仿真验证了改进后车架的弯曲刚度比原来提高了2.1倍，车架的前5阶模态频率均比原来提高，车架的安全性更好。

（4）针对FSAE赛车的车架结构优化方法和流程，可以推广并应用到其它钢管桁架式车架的结构优化及轻量化设计与开发中。

参考文献（References）：

赵文娟. YD02赛车车架结构设计及其轻量化研究 [D]. 秦皇岛：燕山大学，2009.

Zhao wenjuan. Design and Research on the YD02 Racing Car Frame Structure [D]. Qinhuangdao：Yanshan Univer-sity，2009.（in Chinese）

马鸣图，路洪洲，李志刚. 论轿车白车身轻量化的表征参量和评价方法 [J]. 汽车工程，2009，31（5）：403-407.

Ma Mingtu，Lu Hongzhou，Li Zhigang. Theory of Light Car White Body Quantitative Characterization Parameter and Evaluation Method [J]. Automotive Engineering， 2009，31（5）：403-407. （in Chinese）

2015 Formula SAE China Competition Rules and Regu-lations [Z]. SAE China， 2015.

吕品. 汽车车架拓扑优化设计 [D]. 沈阳：沈阳理工大学，2008.

Lü Pin. Topology Optimization on Car Frame [D]. Shen-yang：Shenyang University of Technology，2008. （in Chinese）

赵明皥，王成明. 汽车轻量化技术的应用及发展趋势 [C]// 河南省汽车工程学会第七届科研学术研讨会论文集. 郑州：河南省汽车工程学会，2009：1-4.

Zhao Minghao，Wang Chengming. Application and Deve-lopment Trend of Automotive Lightweight Technology [C]// Automotive Engineering Institute of Henan Province Seventh Annual Research Conference Proceedings. Zheng-zhou：Automotive Engineering Institute of Henan Province，2009：1-4. （in Chinese）