谷物联合收割机脱粒机机架有限元分析及优化

臧世宇 吴崇友++伍扬华

摘要：为校核某型号的谷物联合收割机脱粒机机架的强度特性，运用P/ROE软件建立机架的三维模型，并导入到ANSYS Workbench中进行有限元分析，确定其力学特性，得到该结构的应力、变形云图，找到最大应力产生的部位。结果表明，机架应力分布均匀，最大应力小于其许用应力，满足强度要求，且具有较大富余。最大变形量较小，变化合理，满足要求，并进一步运用拓扑优化方法对机架结构进行优化，优化后的机架质量减少20%，节省了材料，拓扑优化运用在机架设计中是有效的。

关键词：谷物联合收割机脱粒机；机架；有限元法；应力；变形云图；静力学；拓扑优化

中图分类号： S225.3文献标志码： A

文章编号：1002-1302（2016）12-0347-03

收稿日期：2015-11-04

基金项目：国家科技支撑计划（编号：2010BAD01B06）。

作者简介：臧世宇（1990—），男，安徽合肥人，硕士研究生，研究方向为农业装备工程技术。E-mail：524152595@qq.com。

通信作者：吴崇友，研究员，博士生导师，研究方向为耕作与收获机械。E-mail：542681935@qq.com。

随着农业机械化事业的蓬勃发展，谷物联合收割机技术变得更加成熟和完善，但在整体性能特别是可靠性方面与国外收割机仍然具有差距[1]。脱粒清选装置是联合收割机的核心工作部件，主要由机架、脱粒装置、清选装置组成。机架是脱粒滚筒、振动筛、风扇、传动系统的安装基体，作为这些部件的安装基体机架承受这些总成的质量及其传给机架的各种力和力矩，这就要求车架必须具有足够的强度、刚度以保证各运动件之间相对位置准确，以满足产品使用可靠性[2]。在机械行业中对结构进行强度分析的方法主要是数值模拟与试验的方法[3]，其中数值模拟法主要是有限元分析，具有便捷高效的特点，能在产品设计初期对结构的静态特性具有准确预测，有效缩短产品的研发、换代周期；结构拓扑优化是优化领域出现的一种新的研究方向，与其他优化相比，结构拓扑优化能够得到更大的经济效益[4]。现采用有限元分析软件ANSYS Workbench对谷物联合收割机进行有限元静力学分析，得到车架在载荷作用下的应力云图，通过对车架应力及变形图进行分析，找到變形最大处和应力集中处，运用拓扑优化方法对机架进行轻量化设计。

1静力学分析理论基础

线性静态结构分析（line static structural analysis）用于计算在固定不变的载荷作用下结构的效应，它不考虑惯性和阻尼的影响，主要计算固定不变的惯性载荷对结构的影响（如重力与离心力），以及那些可以近似为等价静力作用的随时间变化的静载荷。在经典力学中，物体的通用动力学方程为[[WTHX]M]{ü}+[[WTHX]C]{u[DD（-1]·[DD）]}+[[WTHX]K]{u}={[WTHX]F（t）}，其中[[WTHX]M]为质量矩阵，[C]为阻尼矩阵，[K]为刚度矩阵，{x}为位移矢量，F（t）为力矢量。在线性静态结构分析中力与时间无关，则位移{[WTHX]x}可由矩阵方程[[WTHX]K]{x}={F}解出，假设[[WTHX]K]为一常量矩阵且必须是连续的。材料满足线弹性、小变形理论，边界条件允许包含非线性的边界条件，{F}为静态加载到模型上的力，该力不随时间变化，不包括惯性影响因素（如质量、阻尼等）。

2静态分析前处理

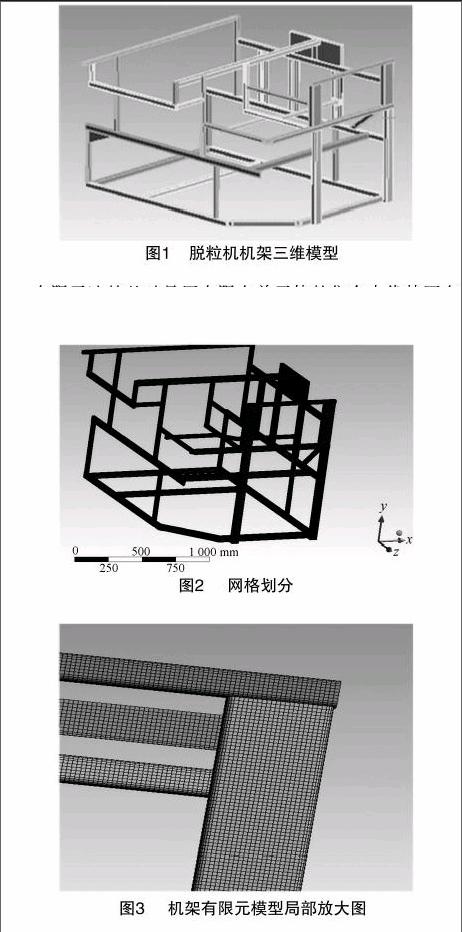
该机架主要是由结构用冷弯矩形空心钢制成的横纵梁焊接而成的，其材质是Q235A号钢，泊松比μ=0.288，弹性模量E=212 GPa，屈服强度σs=235 MPa。在进行有限元静态分析时，首先建立机架的有限元模型，考虑到机架结构的复杂性和建模过程的规律性，直接在ANSYS Workbench中建立机架模型较为困难，因此采用三维绘图软件P/ROE建立机架的三维模型，其参数化的建模方式能有效提高建模效率，缩短设计周期[5]。在建模时，根据零部件的特征，在能充分反映机架结构特性并满足设计精度的前提下，合理简化模型[6]，简化设定为：（1）忽略一些不必要的倒角、圆角并将其简化为直角；（2）忽略机架上的非承载件、焊缝和一些小尺寸结构等。模型建好后通过与ANSYS Workbench的接口将模型导入有限元分析软件中，做到无缝集成，可避免模型先转换成中间格式再导入有限元软件中所造成的某个部件丢失，实现协同仿真。其建立的三维模型见图1。

[FK（W10][TPZSY11.tif]

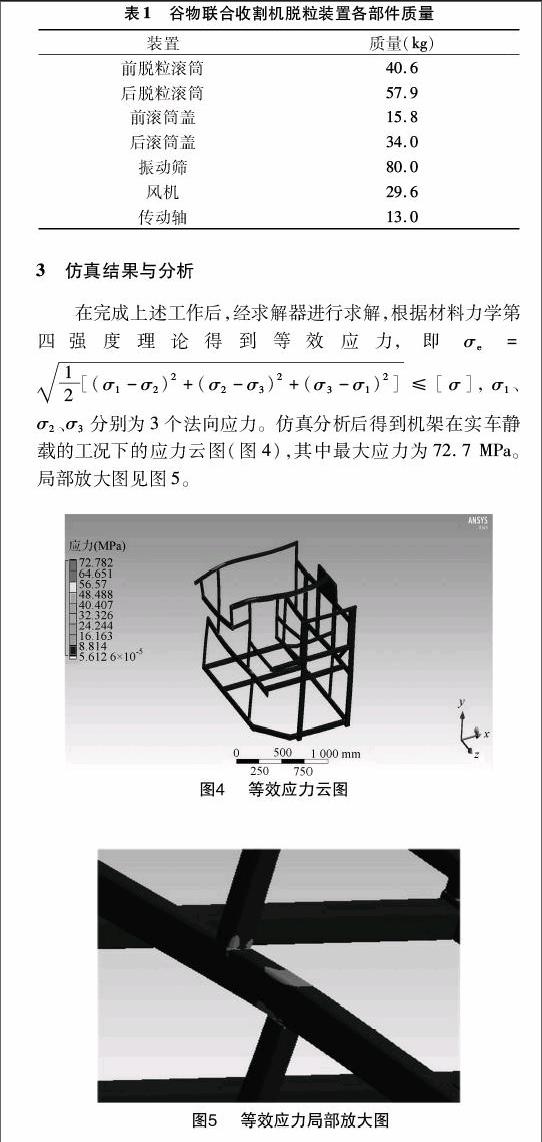
有限元法的基础是用有限个单元体的集合来代替原有的连续体，因此进行模态计算之前应将简化的实体结构划分为有限个单元组成的离散体，单元之间通过单元节点相连接[7]。网格划分是有限元模态分析的重要环节，网格的质量对分析结果具有直接影响，ANSYS Workbench提供了多种划分网格的方法，由于机架结构较为复杂，为保证计算精度在设置好网格相关参数后采用自由划分网格的方法划分网格，划分后的网格共有3 439 451个节点1 157 085个单元体。离散化后形成的有限元网格划分结果见图2，机架有限元模型局部放大图见图3。

在进行有限元分析时，为使数值解有且仅有唯一解，必须消除机架结构的位移，以保证机架结构总刚度矩阵非奇异，因此引入正确的边界条件是获得较高精度解的前提[8]。由于脱粒机机架是连接联合收割机底盘的装置，机架底部用螺栓与收割机底盘固定在一起，可采用固定约束（fixed support）限制其运动。机架上主要安装部件有脱粒滚筒、脱粒滚筒盖、清选风机、振动筛、传动轴。各部件通过轴承座和螺栓与机架连接，各个力可按照静力等效原则以均布载荷的形式施加在各个连接处[9]。机架静态分析主要分析实车静载的工况，实车静载指机架承受额定载重、机架自重的重力载荷，每个单元所承受的载荷按静力等效原则转移到节点上，并在所受约束的节点上根据实际情况设置约束条件[10]。其中，额定载荷包括前后脱粒滚筒、滚筒盖、振动筛、风机、传动轴的自重。各装置质量情况见表1。

3仿真结果与分析

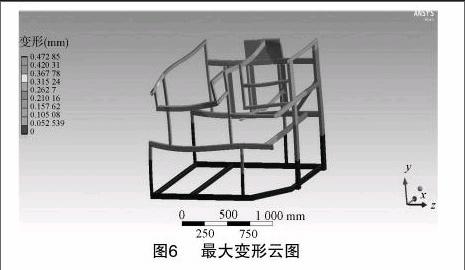
在完成上述工作后，经求解器进行求解，根据材料力学第四强度理论得到等效应力，即σe=[KF（][SX（]12[SX）][（σ1-σ2）2+（σ2-σ3）2+（σ3-σ1）2][KF）]≤[σ]，σ1、σ2、σ3分别为3个法向应力。仿真分析后得到机架在实车静载的工况下的应力云图（图4），其中最大应力为72.7 MPa。局部放大图见图5。

[FK（W12][TPZSY44.tif；S+3mm]

[TPZSY55.tif；S+3mm]

从图6可知，机架的最大变形量为0.47 mm，最大变形处位于后脱离滚筒安装处的后横梁与排草口纵梁相连接的地方；最小变形量为0，主要是位于机架底部。由材料特性可知，Q235号钢的屈服强度值σb=235 MPa，根据一般使用情况可取安全系数n=1.5，计算得出许用应力[σ]=σb/n=157 MPa，通过仿真分析求出最大应力σmax=72.7 MPa<[σ]，可见该机架结构的总体设计满足强度要求，且强度有较大富余，可在满足该强度要求的情况下，对该机架进行进一步优化。

[FK（W10][TPZSY66.tif]

4拓扑优化设计

最优化设计理论和方法在机械设计中得到了广泛运用和深入研究，拓扑优化设计是一种根据给定的负载情况、约束条件和性能指标，在给定的区域内对材料分布进行优化的数学方法。通过优化设计方法可以得到满足约束条件并使目标函数最优的结构布局形式及构件尺寸[11]，拓扑优化设计所需的初始约束条件要求更简单，设计者只须要明确设计域而不须要知道具体的结构拓扑形态，它将整个结构体上的质量分布函数作为优化参数（自动将CAE模型中每个单元的密度作为设计变量），其优化目标是在满足所有给定的约束条件下，根据算法确定设计空间内单元的去留，保留下来的单元即构成最终的拓扑方案，从而实现拓扑优化，其数学模型可表示为：

[JZ]minF（x）=F（x1，x2，…，xn）

[JZ][JB（{]gi（X）=gi（x1，x2，…，xn），（i=1，2，…M）X=（x1，x2，…，xn）T[JB）]。

式中：F（x）为设计变量的目标函数；X为设计变量；gi（X）为状态变量。优化结果的取得就是通过改变设计变量的数值来实现的[11-12]。

在完成静力学分析后，重新选择求解模块，所分析的项目选择为“Shape Optimization”，各约束条件与静力学分析相同，设置优化目标为20%，进行求解运算所得到的优化结果如图7所示。图7显示，可移除的结构主要集中在与底盘机架连接的部位，但在机架的实际设计中还要考虑应力分布问题、结构稳定性问题，这些红色区域并不一定都要全部移除，这些可移除部件的特点是变形量小、强度富余量大。经过优化后，机架的应变、应力并没有提升，而质量却减少了20%，从而节省了材料且提升了产品的经济性。

5结论

割机脱粒机机架进行有限元静力学分析，得到机架的变形、应力云图，并对机架的强度进行校核，在安全系数取1.5时，机架强度满足使用要求，且有较大富余。运用拓扑优化模块对机架进行优化设计，经优化后的机架质量减少了20%，既满足了静刚度要求，也节省了材料。拓扑优化对收割机机架设计具有很强的指导意义和参考價值。但是，拓扑优化只是一种概念设计，而实际的开发设计还须要考虑其他各方面的因素，这也是下一步所研究的方向。

[HS2][HT8.5H]参考文献：[HT8.SS][HJ1.78mm]

[1]胡东方，王想到. 基于有限元的玉米联合收获机底盘车架模态分析[J]. 农机化研究，2015，6（6）：53-55，59.

[2]朱金光，冷峻，丁雄飞，等. 玉米联合收割机机架动力学分析方法的应用研究[C]//国际农业工程大会论文集. 上海：亚洲农业工程学会、中国农业机械学会、全国农业机械标准化技术委员会、中国农业工程学会，2010.

[3]高云凯. 汽车车身结构分析[M]. 北京：北京理工大学出版社，2006.

[4]Bendsoe M P，Sigmund O. Topology optimization：theory，methods and applications[M]. Berlin：Springer，2003.

[5]王鹰宇，姚进，成善宝. 基于ANSYS环境的参数化有限元建模[J]. 机械，2003，30（4）：12-14.

[6]许佩霞，蔡炳芳. 基于ANSYS的全地形车车架结构优化设计[J]. 机械设计，2008，25（12）：56-58.

[7]熊永华，杜发荣，高峰，等. 轻型载货汽车车架动态特性分析与研究[J]. 机械设计，2007，24（4）：60-62.

[8]赵武云，吴劲锋，张锋伟，等. 三轮农用运输车机架动静态特性分析[J]. 农业机械学报，2005，36（11）：29-33.

[9]朱渝春，蹇开林，严波.工程机械底架结构有限元分析的技术处理[J]. 工程机械，2002，33（10）：13-15.

[10]连文香，魏宏安，邵世禄，等. 4U-1400FD型马铃薯联合收获机机架有限元分析[J]. 甘肃农业大学学报，2010，45（5）：129-133.

[11]高东强，毛志云，张功学，等. 基于ANSYS Workbench的DVG850工作台拓扑优化[J]. 机械设计与制造，2011（2）：62-63.

[12]李兵，何正嘉，陈雪峰. ANSYS Workbench 设计、仿真与优化[M]. 北京：清华大学出版社，2012.