基于EMD分解和相关峭度的滚动轴承故障诊断方法研究＊

朱杰平 张永祥 王孝霖 张 帅

（海军工程大学动力工程学院 武汉 430033）

0 引 言

近年来，人们对机械设备滚动轴承进行了广泛的研究并且取得了很大的突破，常用的方法着重于消噪和特征提取.短时傅里叶变换易于观察出信号的瞬时频率的信息，但是它提高了计算的复杂度；小波分析在原信号故障冲击相对明显时，可以获得很好的效果，但是小波分析的频带特性使其难以对一些故障特征进行有效的提取［1－3］.HHT（hilbert－huang transformation）算 法 是 由N.E.Huang等人提出来的，适合于分析非线性、非平稳信号序列，具有很高的信噪比，近年来在信号的分析处理中获得了重要的应用［4－5］.这种算法的核心理论被称为EMD分解，它能使复杂信号分解为有限个确定的本征模态函数（intrinsic mode function，IMF）分量，所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号.

本文利用EMD分解处理非线性、非平稳信号的优势，将滚动轴承上测得的振动信号进行分解，然后，引入相关峭度的概念并对其定义进行了阐述.提出了根据相关峭度进行IMF分量选择的机械设备滚动轴承故障特征提取方法.仿真信号及实验测量的滚动轴承振动信号验证了该方法的有效性.

1 EMD分解的理论介绍和特征提取

1.1 EMD分解的原理

EMD分解的目的就是为了获取IMF分量，假设所有信号都是由IMF分量组成，每个复合信号的产生都是由若干个IMF分量叠加形成.Huang认为，一个IMF分量必须满足2个条件：（1）本征模态函数在整个数据长度范围之内，局部极值点和过零点的数目必须相等，或最多相差一个；（2）在任意时刻点，局部最大值的包络（上包络）和局部最小值的包络（下包络）平均值必须为零.其分解步骤［6］如下.

1）镜像拓展序列，找出信号x（t）所有的局部极值点并画出x（t）的上、下包络线，计算它们的平均值曲线m1（t），用x（t）减去m1（t）得

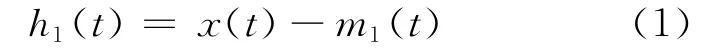
2）若h1（t）满足IMF 的条件，那么h1（t）即为x（t）的第一个IMF分量.若h1（t）不满足IMF的条件，则把h1（t）作为原始数据重复步骤1）直到得到满足条件的分量h1k（t），记c1（t）＝h1k（t）.

3）将c1（t）从x（t）中分离出来，得到第1阶剩余信号r1（t）

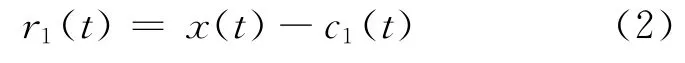
把r1（t）作为新的原信号，重复以上过程.当不能再从rn（t）中提取满足IMF条件的分量时，循环结束.并得到

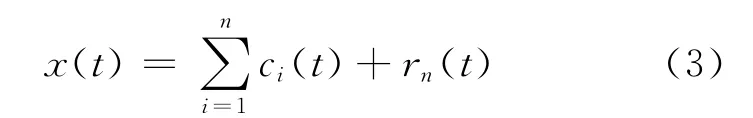
由以上过程可知，原始数据信号可表示为若干固有模态函数分量与一个残余项的和.利用这种关系，通过选取合适的分量进行信号叠加重构，可以对特征信息进行提取.

1.2 相关峭度

由于滚动轴承故障产生的信号还受到周围其他的故障干扰，比如齿轮箱等的故障，这给提取滚动轴承故障信号带来了困难，而相关峭度（correlated kurtosis，CK）进行选取时，利用故障信息的周期性，只与滚动轴承的故障信号相关，因此，将相关峭度引入滚动轴承故障诊断，CK是反映振动信号中周期脉冲信号强度的参数，其计算公式为

式中：yi为信号经EMD分解得到的本征模态函数分量；T为感兴趣脉冲信号的周期；M 为偏移的周期个数.

相关峭度作为一个局部指标克服了峭度无法反映特定信号分量特征的缺点.在给定偏移周期T的情况下，相关峭度能够准确反映信号中感兴趣周期脉冲信号的强度，因此，特别适用于轴承表面损伤类故障.CK值越大，说明信号中感兴趣周期脉冲信号所占的比重越多.

1.3 基于EMD和相关峭度的特征提取方法

相关峭度值的大小通常是反映信号是否携带轴承故障信息的标准之一，当IMF分量的相关峭度比较大时，其包含的轴承故障信息也就比较多.将相关峭度作为IMF分量的选择依据，从分量中获取携带轴承故障信息的振动成分，从而实现对原信号中故障特征的提取.

2 仿真研究

2.1 信号仿真

机械设备滚动轴承发生故障时，测得的信号中往往含有非线性、非平稳信号，可得机械设备滚动轴承内圈单点损伤引起的振动信号模型如下［7］.

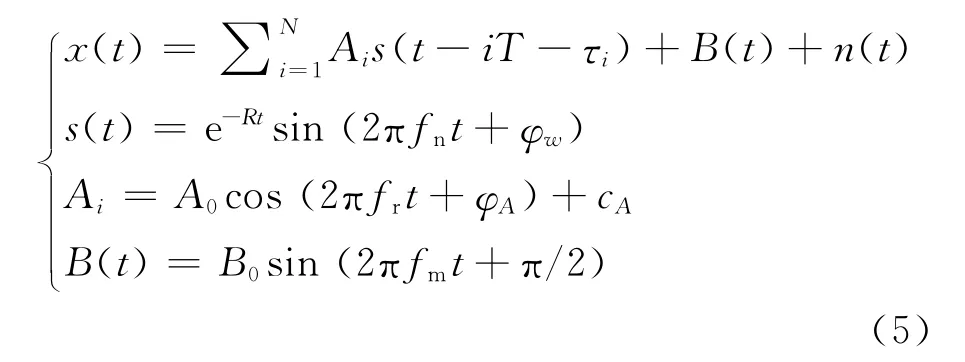
式中：Ai为以1／fr为周期的幅值调制；fr为轴的转频；B（t）为背景谐波分量；fn为系统的自然频率；s（t）为指数衰减脉冲；两相邻冲击的间隔为T；τi为滑移引起的第i个脉冲的周期延迟；A0＝2，B0＝4，cA＝0.5为常数；R 为由系统决定的衰减系数；n（t）为白噪声.

2.2 仿真验证与分析

设采样频率fs为10 800Hz，转频fr为12 Hz，故障频率fi为54Hz.由式（5）可得仿真信号时域波形如图1a），时域波形图中包含明显的谐波分量，故障信号不明显，加上噪声的干扰，难以看出故障冲击.仿真信号平方包络谱如图1b）所示，可以看出解调效果欠佳，故障信号的调制特征没有出来.因此，直接由仿真信号时域波形和平方包络谱不能有效诊断出故障.

对仿真信号进行EMD分解，得到有限个明确的IMF.利用相关峭度式（4）可得各分量的相关峭度值.选取相关峭度值大的分量，并将其进行叠加重构，其时域波形和平方包络谱如图2所示，可以看到明显的故障冲击、故障特征频率及调制特征.因此，该方法能够对轴承内圈故障进行有效的诊断，这充分验证了本文提出的基于EMD和相关峭度的滚动轴承故障诊断方法的有效性.

3 实验研究

3.1 实验装置及轴承故障信号测量

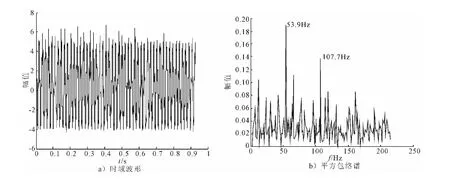
图1 仿真信号

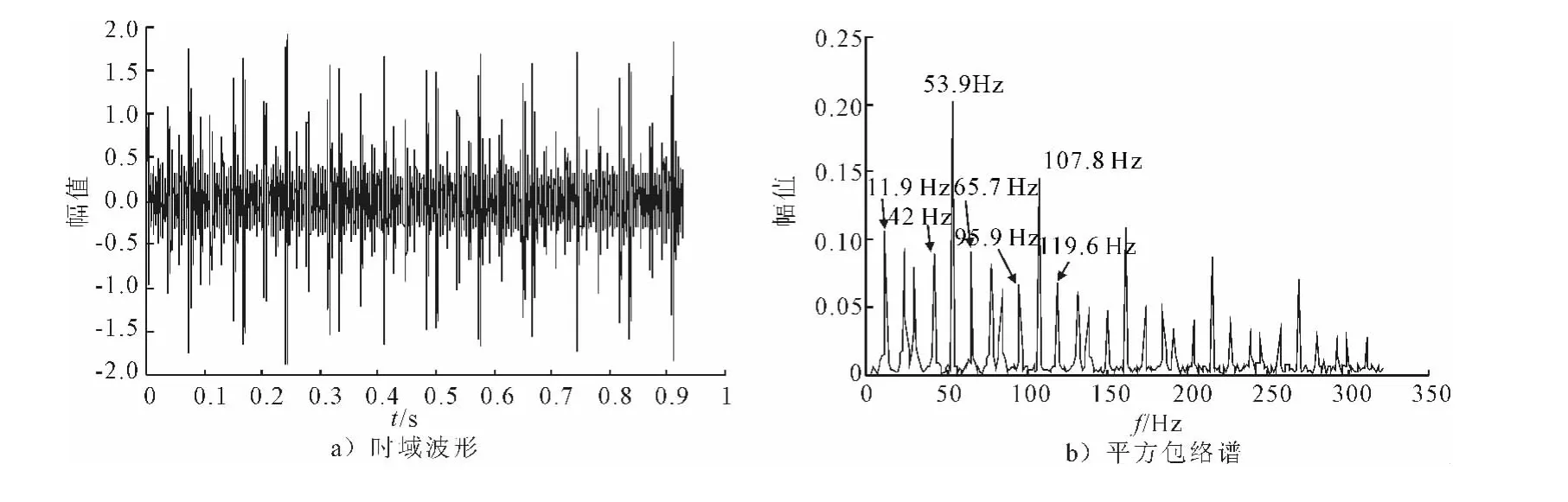
图2 重构信号

滚动轴承故障信号由海军工程大学监测诊断实验室试验装置测量获取.该实验装置由驱动主机及变频控制器、联轴器、减速齿轮、齿轮箱组成.其中，支撑齿轮箱2根轴的滚动轴承为6004，通过调节变频以控制主机的转速，从而控制滚动轴承的转速，通过调节齿轮泵出口油压，改变齿轮箱负载，从而改变滚动轴承负载.滚动轴承有内圈、外圈、滚动体、保持架故障，而最难监测的是滚动轴承内圈故障，因为内圈故障信号需从滚动体传到外圈再传到轴承座上.实验时，应用线切割方法，分别在2个轴承的内圈和外圈上切割一个宽0.1mm、深0.1mm模拟轴承表面损伤类故障.通过实验可测量得到轴承内外圈有故障时对应的振动信号，当轴承转速为2 960r／min时，轴承的内圈故障特征频率为267.4Hz.

3.2 实验分析

实测得到的振动信号的时域波形和EMD分解如图3，可知难以从a）图中分辨出故障周期脉冲，b）图是对实测信号进行EMD分解，图中只画出了前面6个分量.

图3 实测信号

EMD分解将振动信号从高频到低频分解成多个单分量信号和窄带信号，机械设备轴承的诊断信号经过EMD分解后出现了8个IMF分量和1个趋势项.将其分解成为了有限个确定的IMF后，再计算各IMF的相关峭度，相关峭度值曲线如图4所示，选择峭度值大的分量进行叠加重构，重构信号的时域波形和平方包络谱如图5所示，可以从时域波形图中清楚地看到故障周期脉冲以及转频的幅值调制，同时可以从平方包络谱中清楚看到轴承故障特征频率270Hz（理论计算值267.5Hz）及其倍频，平方包络谱中也可以看到转频50Hz（理论计算值49.3Hz）.根据其可以诊断轴承故障为内圈故障.

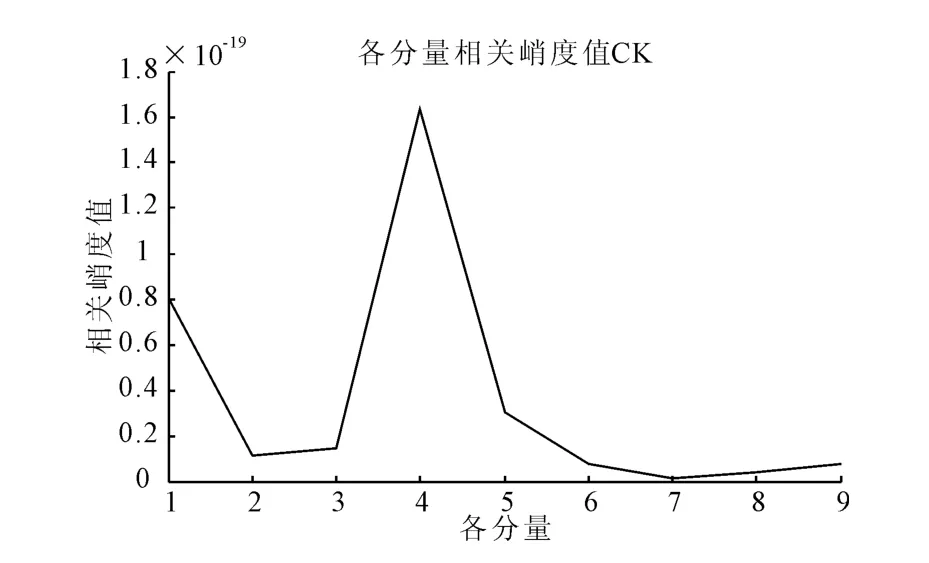
图4 相关峭度值曲线

通过运用基于EMD和相关峭度的滚动轴承故障特征提取方法，对故障信息进行了有效提取，并判断出了故障类型，证明了该方法的有效性.

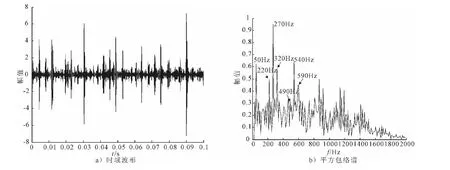
图5 重构信号

4 结束语

本文在分析EMD分解和相关峭度的基础上，提出了结合EMD分解和相关峭度的滚动轴承故障特征提取方法，即首先通过EMD分解把信号分解为有限个确定的IMF分量，然后对提取出的IMF分量进行相关峭度值计算，选择相关峭度值大的IMF分量，并对其进行叠加重构，提取出滚动轴承故障信号.利用该方法对仿真信号进行处理，验证了该方法的有效性.结果表明，该方法能够有效提取轴承故障信号，对于轴承故障的监测和诊断是可行的.

［1］赵学智，叶邦彦，陈统坚.基于小波奇异值分解差分谱的弱故障特征提取方法［J］.机械工程学报，2012，48（7）：37－48.

［2］陈荣刚，赵桃峰，莫晋凯.EMD分解滤波特性在航空发动机平稳振动信号分析中的应用［J］.四川兵工学报，2010，31（7）：63－65.

［3］张梅军，陈 灏，曹 勤，等.EMD分解、分形理论和RBF神经网络相结合的轴承智能故障诊断研究［J］.设计与研究，2012，39（11）：10－15.

［4］隋文涛，路长厚，张 丹.基于加权FCM算法的轴承故障诊断［J］.武汉理工大学学报：交通科学与工程版，2010，34（1）：72－75.

［5］LY C，RANNEY K，TOM K，et al.Effectiveness of empirical mode decomposition based features compared to kurtosis based features for diagnosis of pinion crack detection in a helicopter［C］.Annual Conference of the Prognostics and Health Management Society，2010：1－10.

［6］GEOFF L McDonald，ZHAO Q，ZUO M.Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection［J］.Machanical Systems and Signal Processing，2012，33：237－255.

［7］MING Yang，CHEN Jin，DONG Guangming.Weak fault feature extraction of rolling bearing based on cyclic wiener filter and envelope spectrum［J］.Machanical Systems and Signal Processing，2011，25：1773－1785.