基于优化理论优选柴油机燃烧模型经验参数的方法研究

孙 俊 涂 环

（武汉理工大学能源与动力工程学院 武汉 430063）

0 引 言

在内燃机工作过程模拟的研究中，零维燃烧模型兼顾了计算的便捷性与准确性，在大型发动机的整机工作过程模拟和整机性能优化计算中广为应用.零维模型中需要通过经验公式描述燃料的放热规律，一般采用双韦伯函数进行燃烧放热率的模拟.双韦伯函数中含有燃烧始点、燃烧持续角、燃烧品质因素等参数，这些经验参数根据机型的不同变化范围较大，而这些经验参数的选取对模型的正确性有至关重要的影响.以往对这些参数是选取通过2种途径：（1）凭经验选取，该方法比较盲目，计算结果与实测值出入较大；（2）根据不同经验参数的组合进行正交试验［1－2］，但由于试验数量有限，得到的是较优解而不是最优解.为此，本文提出一种运用优化理论，利用柴油机主要性能参数，如最高爆发压力、平均指示压力、压缩终点压力等，优选双韦伯函数中经验参数，进而准确计算柴油机示功图的方法.

1 计算方法

1.1 优化模型

双韦伯函数将燃烧分成预混合燃烧和扩散燃烧两部分，燃烧速度的公式表达如下［3］.

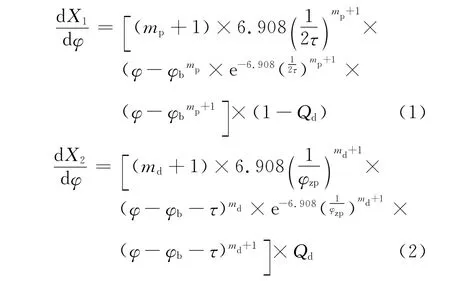
准确模拟实际的燃烧放热规律需要优选双韦伯函数中的6个经验参数：燃烧始点φb、燃烧终点φe、预混合燃烧持续角φzp、扩散燃烧的燃料分数Qd、预混合燃烧品质因素mp、扩散燃烧品质因素md.

计算的问题是根据柴油机的主要性能参数，如最高爆压pz、压缩终点压力pcom、平均指示压力pi等参数，优选双韦伯函数中的φb，φe，φzp，Qd，mp，md等6个经验参数，使得双韦伯函数能够准确地描述柴油机实际的燃烧速度，进而使仿真计算的示功图与实测示功图吻合.

此参数优选问题归纳如下优化计算模型.优化目标：最高爆压pz，压缩终点压力pcom，平均指示压力pi与实测值最接近.

设计变量：XT＝［φb，φe，φzp，Qd，mp，md］

约束条件：｜texh－texh（M）｜≤Δt

由于排温的仿真计算值与实测值有一定误差，故列入约束条件中，pz，pcom，pi，texh分别表示仿真计算的最高爆压、压缩终点压力、平均指示压力以及排温，pz（M），pcom（M），pi（M），texh（M）分别表示为实测的最高爆压、压缩终点压力、平均指示压力以及排温.

1.2 优化算法

建立的优化模型属于多变量多目标有约束非线性的优化问题，此外，该优化模型的设计空间具有非连续性：在Matlab编制的示功图计算程序中，仿真步长为每度曲轴转角，所以双韦伯函数的6个参数中，燃烧始点φb、燃烧终点φe这2个参数必须取整数，使得优化模型的设计空间含有整型变量且具有不连续性.针对该优化模型的具体特征，采用Isight优化软件提供的改进非支配解排序的多目标遗传算法（NSGA II）进行求解，该算法适用于求解高度非线性及设计空间具有非连续性的优化问题［4］.

NSGA的基本原理是基于对个体的几层分级实现种群的非支配排序，在选择操作执行前，群体根据支配与非支配关系排序，所有非支配个体作为一类处理，它们是共享虚拟适应度值的，然后对剩余的个体进行分级并赋予相应的虚拟适应度.NSGA－II算法由Deb等人提出，是以NSGA为基础进行改进，改进的内容主要包括：（1）采用快速非支配排序过程；（2）精英保留策略；（3）无参数小生境操作算子.图1给出了NSGA II算法的流程示意图［5］.

2 优化平台

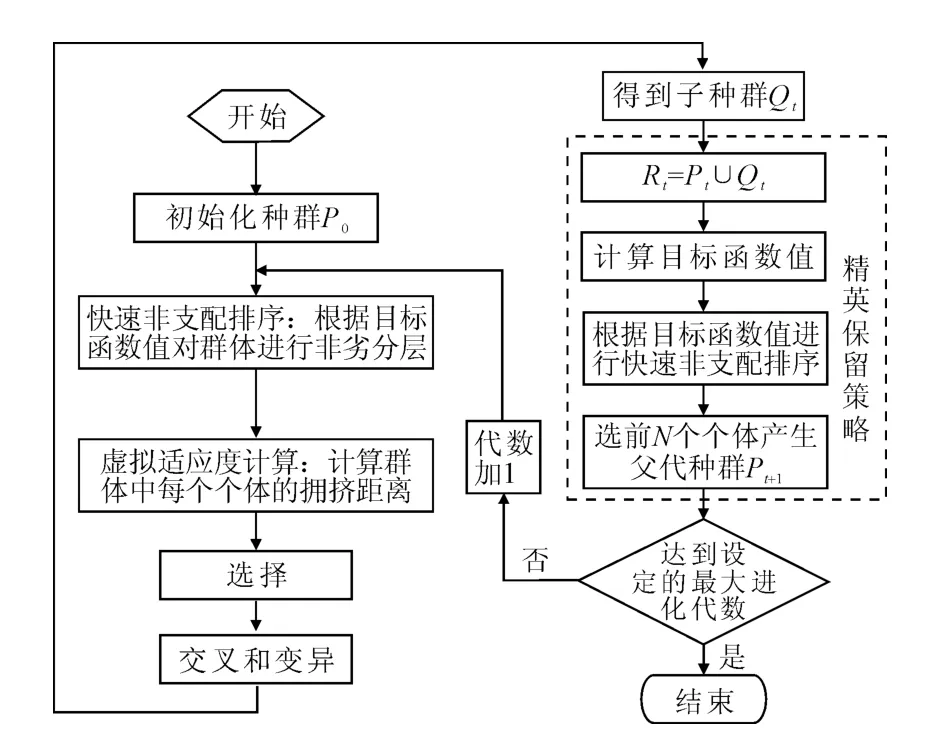
图1 NSGA II流程图

本文基于Isight－Matlab联合仿真优化平台［6－7］进行优化模型的建立与求解，见图2，优化流程见图3.在Isight－Matlab联合仿真优化平台中，通过优化软件Isight驱动Matlab实现优化计算.优化流程可简单概括为：Isight软件中的Optimization1模块读取 Matlab输出的pz，pcom，pi，texh等参数，同时，按照预设的优化算法评价目标函数并进行参数寻优，得到更新的参数，并驱动Matlab对该新方案进行计算，如此循环直至满足迭代停止准则，获得最优解.

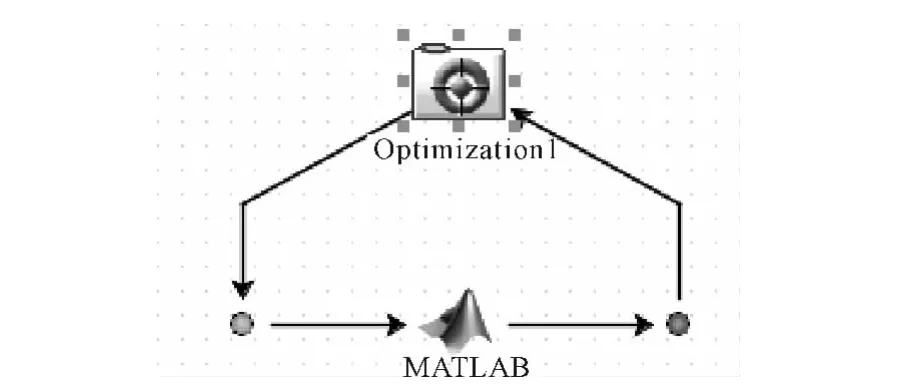
图2 Isight－Matlab联合仿真优化平台

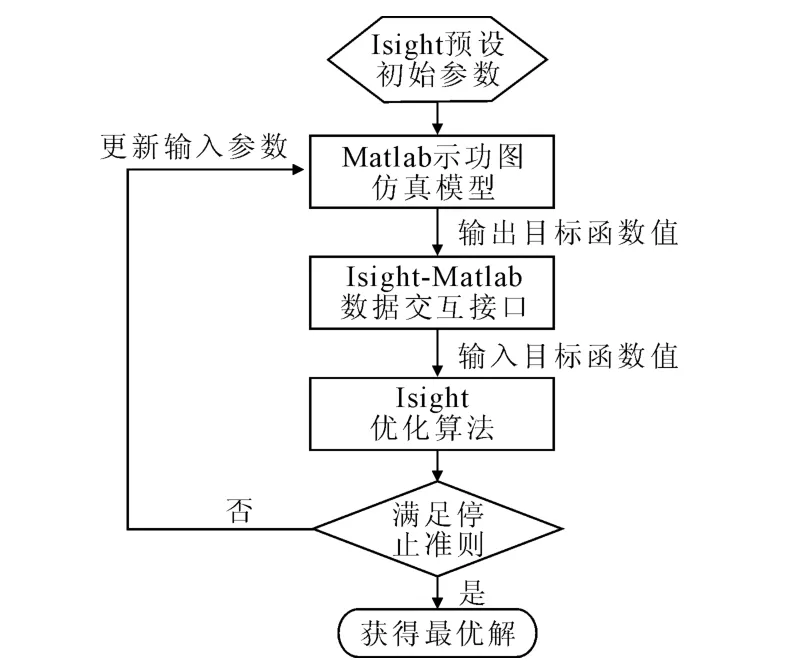
图3 Isight－Matlab联合仿真优化流程图

3 计算实例

本算例以 MAN B＆W 公司的12K98ME－C型低速二冲程船用柴油机标定工况下的台架试验数据作为优化目标，见表1.表2给出了设计变量的上、下限，其取值参考了文献［3］提供的经验数据.约束条件为｜texh－texh（M）｜≤Δt.式中：texh（M）＝370℃，Δt＝20℃.

表1 优化目标 MPa

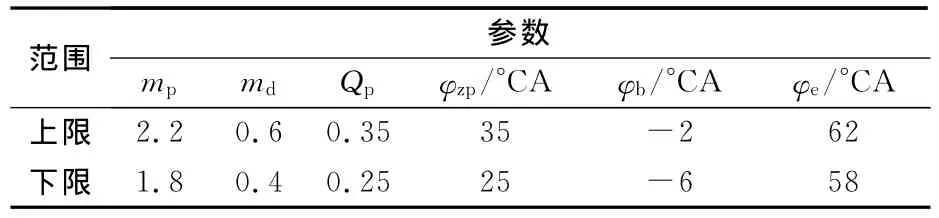
表2 设计变量的上、下限

在Isight优化平台中，采用改进的非支配解排序的多目标遗传算法（NSGA II）求解优化模型，参数设置示见表3.NSGA－II的迭代次数等于种群规模和进化代数的乘积，进行400次迭代计算后得如图4所示的Pareto解集，共含有95个解.

表3 NSGA II方法参数设置

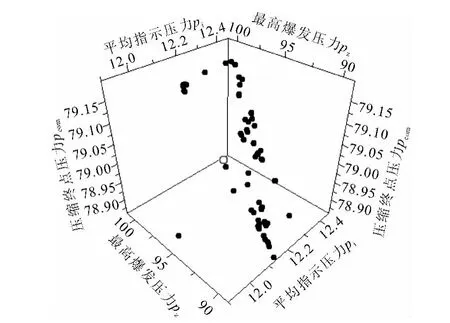
图4 NSGA－II解得的Pareto解集

多目标优化问题需要综合权衡Pareto解集包含所有解，并挑选一个最优折衷解作为最终解，采用线性加权和法在解集中选取一个最优解，目标函数为

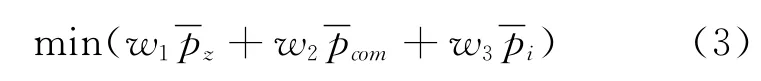
式中：w1，w2和w3分别为最高爆发压力pz、压缩终点压力pcom和平均指示压力pi的权系数，且取值均为1和分别是量纲－的量化后的最高爆发压力、压缩终点压力和平均指示压力，分别由最高爆发压力、压缩终点压力和平均指示压力除以其各自可能取到的极小值得到.最终优化结果示于表4.

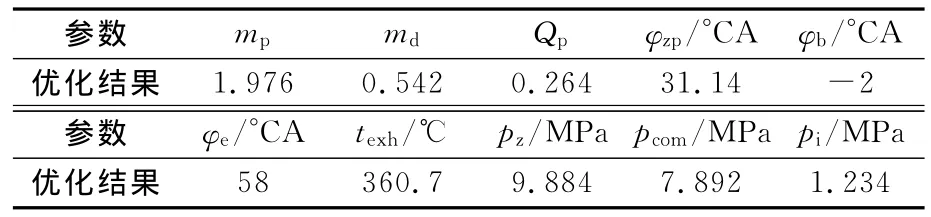
表4 最终优化结果

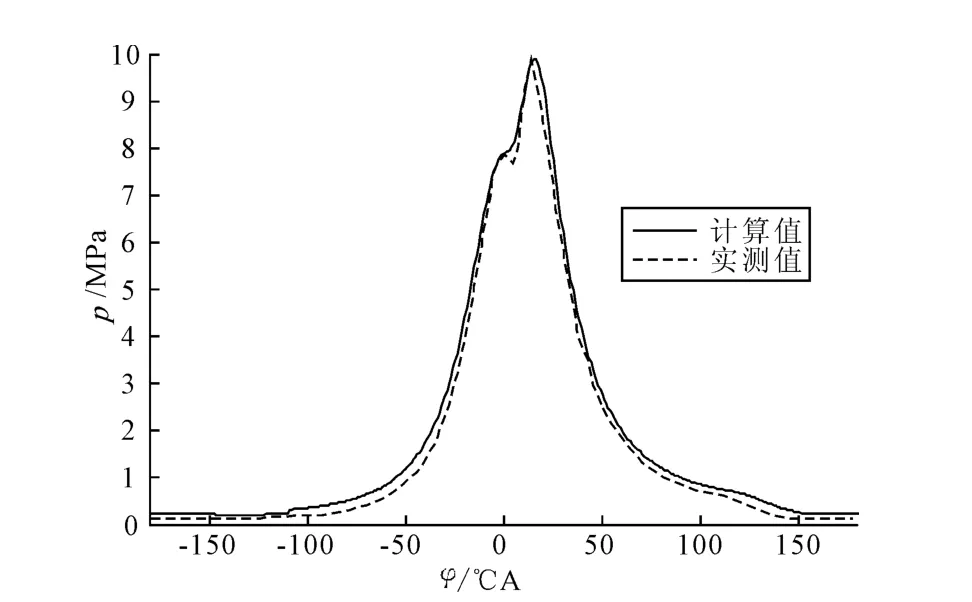
图5 计算示功图与实测示功图

将根据优选参数计算得到的示功图与实测示功图进行对比，见图5.由图5可见，在燃烧始点与燃烧终点之间的阶段，仿真计算的曲线与实测曲线吻合，验证了优选得到的经验参数的准确性.

4 结束语

文中以零维燃烧模型中双韦伯函数的6个经验参数为优化变量，以最爆发压力、平均指示压力、压缩终点压力等性能指标的与12K98ME－C型船用柴油机实测值最接近为优化目标建立优化模型.在Isight－Matlab联合仿真优化平台的支撑下，借助改进的非支配排序遗传算法（NSGA－II），优选双韦伯函数中的6个经验参数，根据优选参数计算得到的示功图与实测示功图基本吻合.本文提出的通过优化算法确定经验参数的方法，可以实现达到减少选取经验参数的盲目性、提高工作效率的目的.

［1］孙 民，于学浒，潘小萍.通过柴油机性能参数确定示功图方法的研究［J］.大连理工大学学报，1996，36（5）：629－631.

［2］邓名华，范维澄，于善颖.柴油机准维燃烧模型中经验参数确定的研究［J］.内燃机学报，2000，18（2）：149－152.

［3］朱访君，吴 坚.内燃机工作过程数值计算及其优化［M］.北京：国防工业出版社，1997.

［4］Alex Van der Velden.iSIGHT user’s guide［M］.Dassault Systèmes Simulia Corp，2011.

［5］冯士刚，艾 芊.带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用［J］.电工技术学报，2007，22（12）：146－151.

［6］何 勇.考虑动态响应的全船结构多目标优化研究［D］.上海：上海交通大学，2012.

［7］冯佰威，刘祖源.基于iSIGHT的船舶多学科综合优化集成平台的建立［J］.武汉理工大学学报：交通科学与工程版，2009，33（5）：897－899.