基于随机需求的集装箱空箱调度研究＊

蔡佩林 涂建军

（广东交通职业技术学院 广州 510800）

0 引 言

集装箱供求矛盾日益突出，空箱调运管理成为急需解决的重要课题.每个地区之间贸易的不平衡、货物对于箱型的选择的不平衡以及各港口集装箱出口需求的不同，使得船公司有必要在经营的航线内的各港口之间进行空箱的相互调拨.国内外很多学者对空箱调运问题研究较多，对用内陆集装箱运输应用了多目标规划法，动态、随机方法、网络化方法来解决空箱调运问题［1－6］；海运应用数学仿真方法揭示成本、收入等经济应诉以及船舶装载能力对集装箱空箱调运策略的影响机制［7］，同时建立空箱调运模型确定模型的网络优化［8－9］，以及讨论在多式联运网络下长期规划对空箱管理的影响［10－11］.

解决空箱调运问题的方法之一是船公司与集装箱租赁公司相互合作，对于集装箱租赁公司为了提高客户的满意度，会在港口堆场存放一定的集装箱以满足船公司的需求.租赁公司对于港口集装箱存储量进行合理调度以满足船公司的多变需求，这一点研究较少，本文针对租赁公司在不同港口间的调度策略构建相应模型，使其达到港口集装箱总存量最低，利润最大的目的，并通过实证分析为租赁公司不同港口间的集装箱的调度策略提供参考价值.

1 模型描述

本文考虑某一租箱公司（以下简称“A公司”）的两个集装箱港口的联合调度问题.设A公司的2种类型（如20′和40′）的集装箱为i，j＝1，2，各港口的存量为Qi，存储成本为ci.这2个港口所在地区对该种集装箱的需求量为Di，由于需求量事先无法准确预计，故为随机变量，2个随机变量服从定义域在［D1×D2］上的联合概率分布，即其联合概率分布函数为F（x1，x2），联合概率密度为.如单独考虑两个地区的集装箱需求量，则可用上述其分布函数的边缘概率分布函数Fi（x）和边缘概率密度fi（x）来反映.

该种集装箱在各地区的租箱费为ri，显然ri＞ci.该种集装箱在各地区的缺箱成本为pi，且pi≥0；其他应收费用si，si＜ci.

由于是同一类型集装箱，且各地的需求量不定，故可考虑不同港口之间的调配，以减少各港口的存储量.集装箱从港口i到港口j的转运价格为hij，转运成本为τij，转运量为Tij.显然，集装箱从港口i到港口j的转运价格必须低于集装箱在港口j所在地区的租箱费和缺箱成本之和，否则转运对于港口j而言将是不经济的；同样，港口i从转运中所得的受益，即转运价格减去转运成本必须大于集装箱在港口i所在地区的其他应收费用，否则转运对于港口i而言将是不经济的.因此，hij∈［si＋τij，rj＋pj］.

为方便表述，本文定义符号x＋＝max（x，0）.这样，从i到j的转运量Tij为j未满足的需求（Dj－Qj）＋和i多余的存量（Qi－Di）＋两者中较小的那个量所决定的，即Tij＝min［（Dj－Qj）＋，（Qi－Di）＋］.

因此，该集装箱在港口i所在地的实际租箱量Ri＝min（Di，Qi）＋Tji；港口i的剩余存量Ui＝（Qi－Di－Tij）＋；港口i的缺箱量Zi＝（Di－Qi－Tji）＋；港口i的利润：πi（Qi，Qj）＝E［riRi＋（hij－τij）Tij－hjiTji＋siUi－piZi］－ciQi.

港口i和j的目标为各自最大化利润，决策变量为存储量.

2 模型构建

本文主要构建3个模型：各港口独立经营下（以下简称“模型1”）、各港口统一调度下（以下简称“模型2”）、各港口单独调度下（以下简称“模型3”），其中第3个模型分3种情况讨论（各港口之间的转运价一定、各港口独自制定转运价、公司总部制定各港口之间的转运价格.

2.1 各港口独立经营下（港口之间无调拨）的调度策略

A公司现有的调度策略为各港口独立运作，相互之间不存在调拨转运，即Tij＝Tji＝0，此时各港口的利润为：

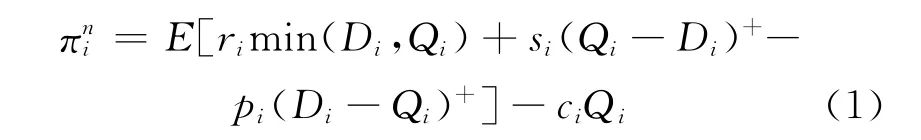
各港口最大化各自的利润，即

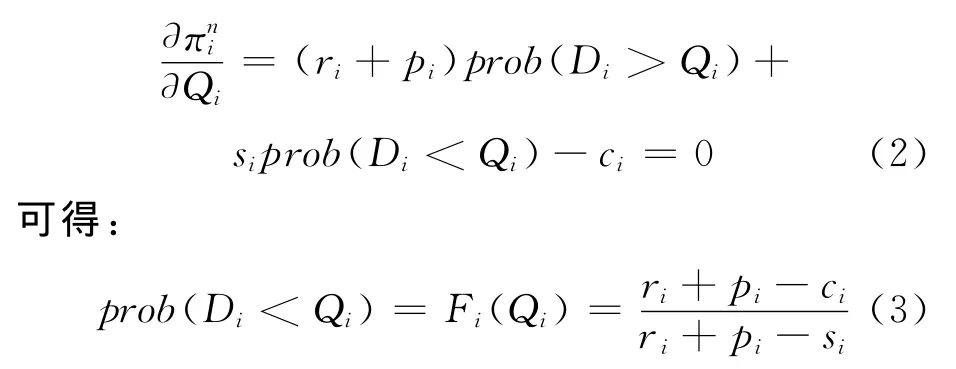
在确定各港口需求量的概率分布函数之后，可根据（3）式求出个港口的最优存储量Qi.

2.2 各港口统一调度下的调度策略

由于各地区需求随机，因此在上述独立经营，无调拨转运的调度策略下有可能出现有的港口存储过多，而另一个港口同时缺箱的情况.这样不可避免地会造成各港口安全存储量的增加，从而增加了成本，浪费了资源.由于i和j租赁的是同类集装箱，因此如果对它们进行统一调度，以一个港口多余的存储量去弥补另一个的缺箱需求，则可以同时达到既减少存储量，又避免缺箱的发生，使i和j达到双赢的效果.

如果调拨转运由A公司总部统一调度，则此时公司总部关心的是i和j总利润的最大化.此时总利润为：

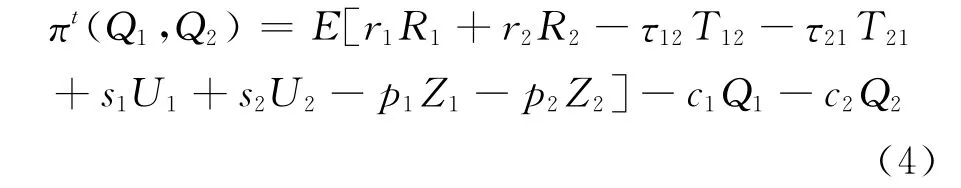
为求解上述利润的最大化问题，共分6种情况：（1）D1＞Q1且D2＞Q2；（2）D1＞Q1且D2＜Q2且D1－Q1＞Q2－D2；（3）D1＞Q1且D2＜Q2且D1－Q1＜Q2－D2；（4）D1＜Q1且D2＞Q2且D2－Q2＞Q1－D1；（5）D1＜Q1且D2＜Q2且D2－Q2＜Q1－D1；（6）D1＜Q1且D2＜Q2.

根据上述情况分别求出i和j各自的实际租箱量、存储量和缺箱量，代入式（4）得出6种情况的i和j的总利润分别为

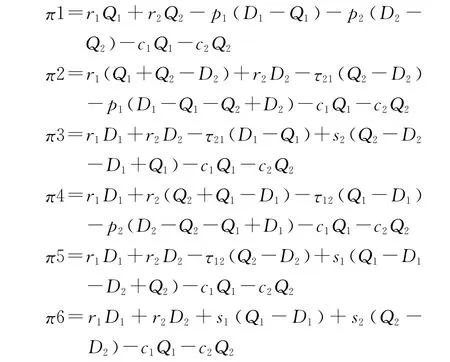
综合这6种情况有

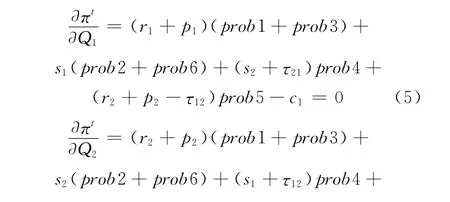
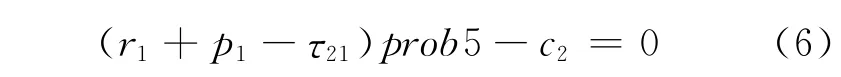
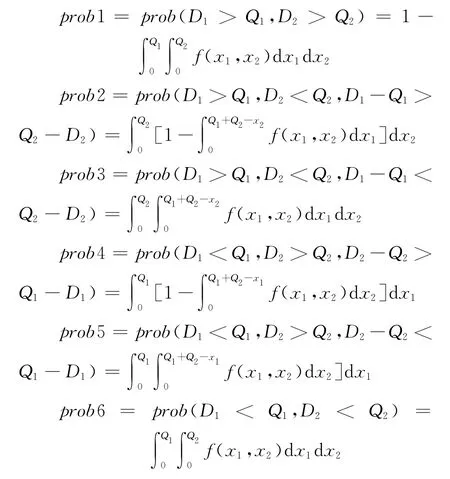
为简化上述表达式，令prob6＝αi（Qi），

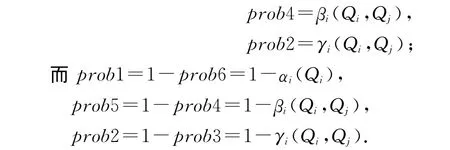
则求解（5）和（6）组成的关于Q1和Q2的二元方程组可得i和j的最优存储量，即：

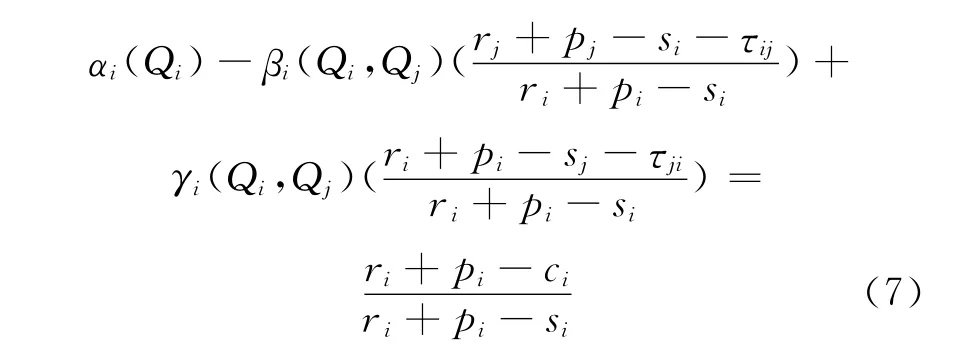
根据给定的需求联合概率分布函数F（x1，x2）可得此时两个港口的最优存储量.

2.3 各港口单独调度下的调度策略

由于各地市场有所差异，市场环境变化较快，为加快各港口对各自市场信息的反应速度，A公司有将各港口代表处办成独立经营，自负盈亏的子公司的想法.当各港口成为独立经营的子公司后，A公司总部将不能再用统一行政命令来规定各港口的存储量和相互之间的调拨量，而必须由各港口自己决定各自的存储量，并通过相互之间的博弈来确定他们之间的调拨量.

各港口调拨多余集装箱量的转运价的确定可能有3种情况：（1）转运价由相互之间的运输成本，即由市场所确定，此时各港口不能控制转运价，而只能作为价格的接受者；（2）如果某个港口对该种集装箱的租赁在当地具有一定的垄断地位，则他可以决定该种集装箱转运价；（3）A公司总部虽然不能决定各港口的存储量，但可以通过对各港口施加一定的影响力来影响各港口之间的集装箱转运价，即转运价由A公司总部来确定.在上述三种不同的转运价下，各港口的生产和调度策略将是完全不同的.因此本节将对这三种不同情况下各港口的生产和调度策略进行分析.

2.3.1 各港口之间的转运价一定

1）博弈模型的建立 当各港口独立经营时，各自的调度策略将受到其它港口的牵制，即港口相互之间存在竞争博弈关系，因此本文运用博弈论的相关理论［12］和方法来解决各港口独立经营下的库存问题.

一般来讲，博弈存在着如下几个要素.

局中人 就本文而言，局中人为集装箱港口1和2.

局中人的策略（strategies）空间 即每个局中人可供选择的可行方案集.每个局中人一般有若干个策略可供选择，他们构成了该局中人的纯策略空间.就本文而言，局中人的策略为各港口的存储量Qi.

每个局中人的盈利函数 局中人的盈利与自己所选择的行动有关，也与其他局中人的选择有关.就本文而言，局中人的盈利函数为各港口的利润函数πi（Q1，Q2）.

博弈的均衡 Nash均衡是非合作博弈均衡的基本概念，本文各港口间调度博弈的Nash均衡表述如下：如果对于港口i，是在给定另一个港口j选择其最优策略情况下的最优策略，即∈argQimaxπi（Qi，），i＝1，2，那么为港口1和2间调度博弈的Nash均衡.

2）博弈模型的求解 当2个港口各自独立运作，各港口关心的是各自利润的最大化.此时各港口的利润为

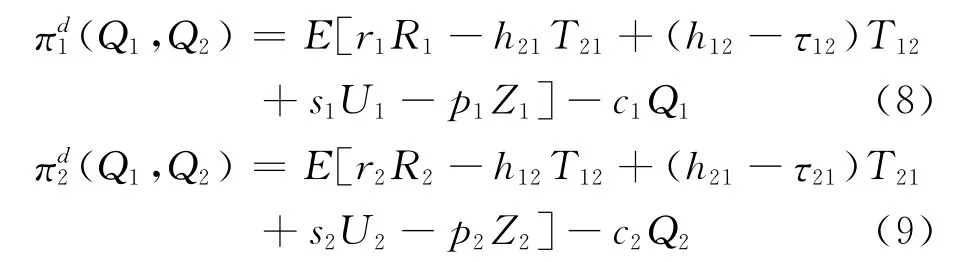
各港口选择常量来最大化各自利润，即

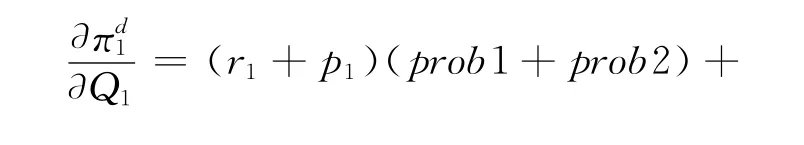
利用与2.2同样的记号，可得上述式（10）和式（11）组成的关于Q1和Q2的二元方程组的解如下.

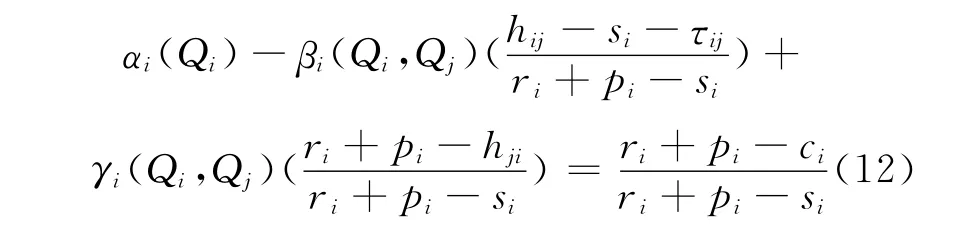
根据给定的需求联合概率分布函数F（x1，x2）可得此时两个港口的最优存储量.

2.3.2 各港口独自制定转运价

因为Tij≥0，所以由各港口的利润函数（Q1，Q2）可知，为hij的增函数，为hji的减函数.而hij∈［si＋τij，rj＋pj］，所以当各港口独自定价时，又可分为两种情况：

1）当转运价hij由港口i决定，即由输出多余存储的港口所决定.由于为hij的增函数，所以hij＝rj＋pj，将上述转运价代入式（12）可得此时i的最优存储量为

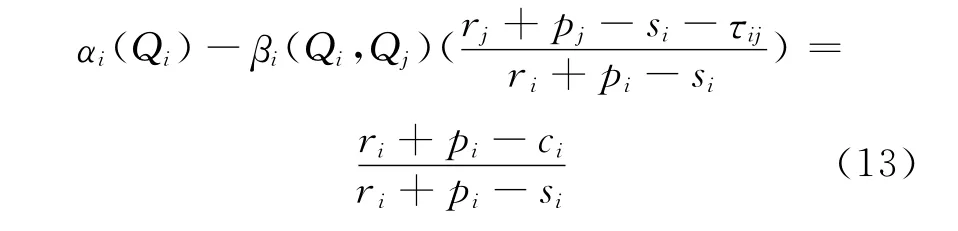
而此时j的最优存储量为

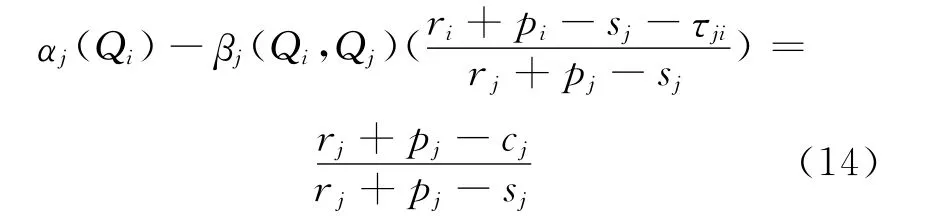
2）当转运价hij由港口j决定，即由接受其它港口多余存储量的港口所决定.由于为hji的减函数，所以hji＝sj＋τji.将上述转运价代入式（12）可得此时i的最优存储量为：

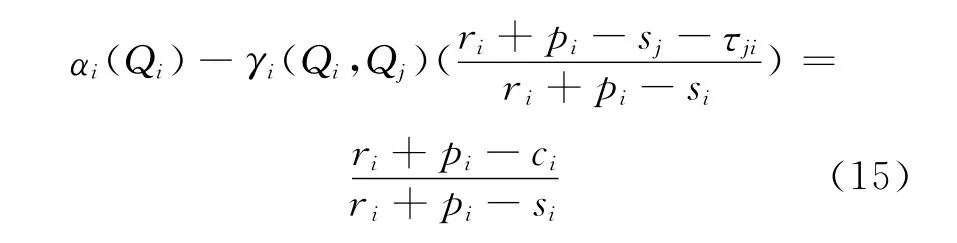
而此时j的最优存储量为：

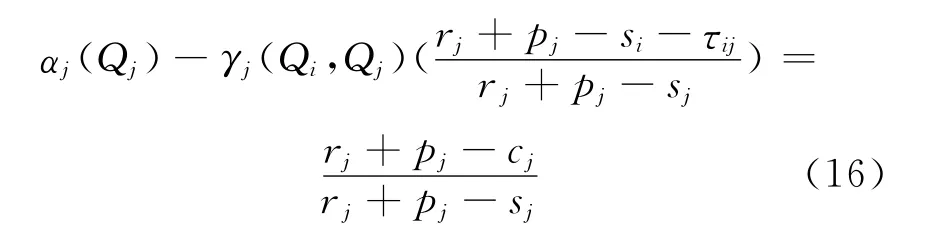
根据给定的需求联合概率分布函数F（x1，x2）可得上述两种情况下2个港口的最优存储量.

2.3.3 公司总部制定各港口之间的转运价格

由于2个港口制定的转运价之间存在一定的差异，为减少两者的分歧，缩短两者的谈判时间，A公司总部可以介入转运价的制定.此时，A公司总部的目标仍然是最大化整体的利益，即两个港口的利润总和.此时A公司总部的目标函数仍为式（4），最大化2个港口利润总和的存储量必须满足式（7）；而同时当2个港口可以单独决策，即以最大化各自利润为目标的存储量必须满足式（12），因此A公司总部可以通过调整转运价hij来间接调控各港口的存储量，使各港口的决策符合整体最优的目标.此时，Qti＝Qdi，即式（7）等于式（12），可得

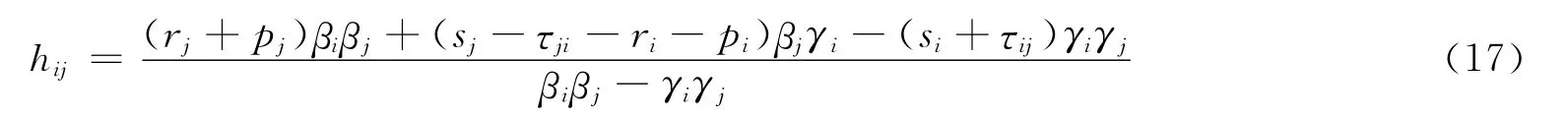
这样，在各港口各自独立经营时，A公司总部可以通过间接调控措施，即转运价来使各港口的决策行为符合整个集团的利益，达到整体最优.

3 实证分析

3.1 A公司集装箱随机需求量的统计分析

3.1.1 集装箱需求量的样本

A公司在2个地区各有1个集装箱港口：A1和A2.选取这2个集装箱港口所在地区过去60d的租箱数据，见表1.

3.1.2 集装箱需求量随机分布的检验方法及结果

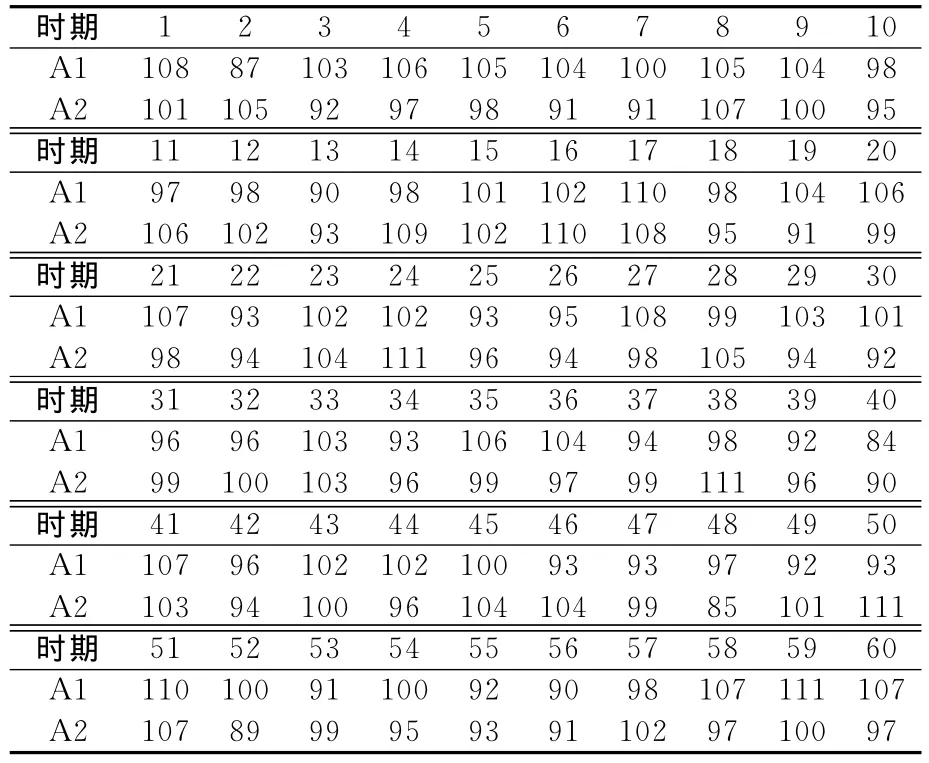
表1 集装箱港口的历史需求数据 TEU

为了确定A1和A2集装箱需求量的随机分布类型，本文使用非参数检验中的柯尔莫哥洛夫－斯米尔诺夫检验法（K－S检验）.

假定A1和A2集装箱需求量服从正态分布，运用统计软件SPSS11.5，对上述60d的样本需求量进行K－S检验，结果为A1的集装箱需求量服从均值为99.566 7TEU，方差为38.76TEU的正态分布；A2的集装箱需求量服从均值为98.916 7TEU，方差为36.79TEU正态分布.

3.2 运用库存控制模型前后的比较

A1和A2现有集装箱的租箱费为40元／TEU，库存成本共为20元／TEU，缺箱成本暂不考虑，集装箱其他应收费用为10元／TEU，A1和A2间的转运成本为2元／TEU.根据上述对A1和A2集装箱需求量的统计分析结果，结合第2部分模型构建的各种调度模型，计算各种调度策略下A1和A2的集装箱存储量，以及利润.结果见表2.

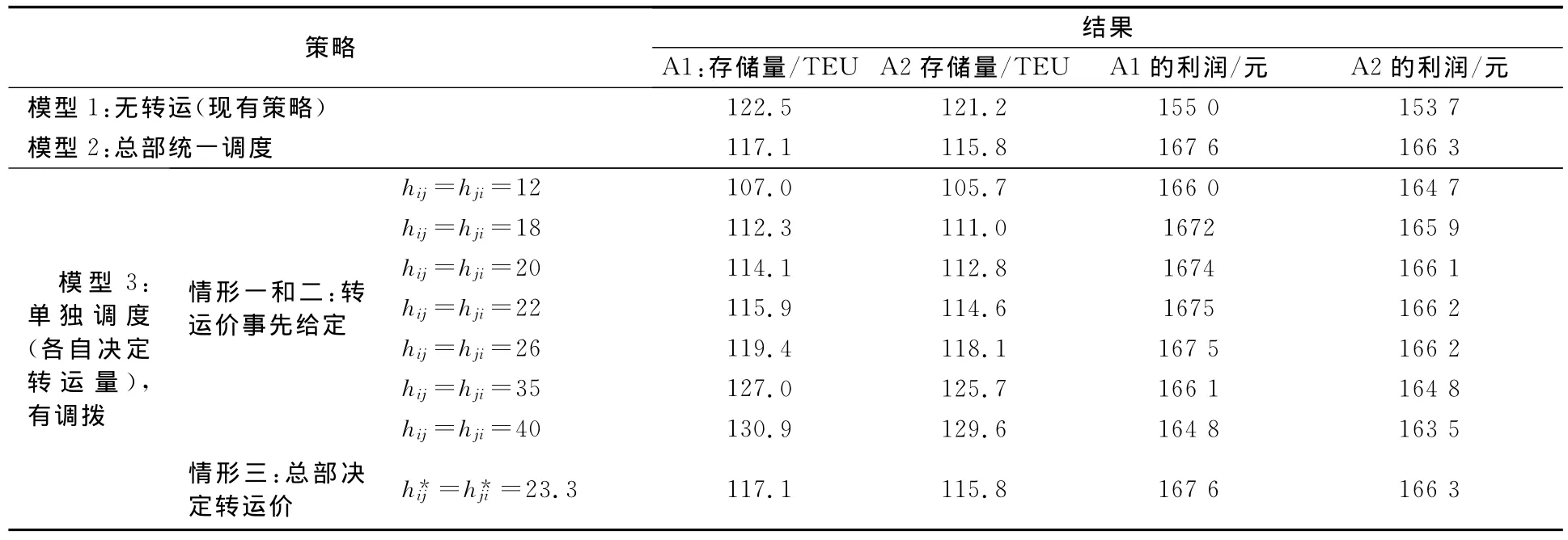
表2 运用调度模型前后的比较结果

需要说明的是，因情形一转运价由市场确定，为了使结果更具合理性，计算时列出多个转运价进行比较分析，与情形二合在一起.从表2可见，模型2和模型3中的情形三的结果是相同的，总体集装箱存储量最低，利润最大.通过运用调度模型前后的比较结果可见：A1和A2各自决定转运量，总部决定转运价的调度策略可取得最优的整体利润，比A公司现有调度策略所取得的整体利润高6.9%，而集装箱存储总量减少4.4%.

4 结束语

从上述3种集装箱空箱的调度模型中可以看出，各港口统一调度下（港口之间有调拨）的调度策略，和各港口单独调度下（港口之间有调拨），在公司总部制定各港口之间转运价格的调度策略这两种调度策略是等价的，且这两种调度策略是各种调度策略中最优的，可以获得公司总体集装箱存量最小，整体利润最大的效果.因此，租赁公司今后的调度模式应向该方向转换.对于本文集装箱港口调度策略模型中，可扩大港口数量，运用相应数学方法可进一步研究，也可应用于船公司的港口间集装箱的调度研究.

［1］李维斌.公路集装箱运输调度算法研究［J］.中国公路学报，1995，9（1）：63－71.

［2］TEOOR G C，MICHEL G，PIERRE D.Dynamic and stochastic models for theallocation of empty containers［J］.Journal of the Operational Research Society，1992（2）：102－126.

［3］WHITE W W，BOMBERAWLT A M.A net work algorithm for empty freight car allocation［J］.IBM System Journal，1969，15（2）：147－169.

［4］HOLMMBERG K，JOBORN M，LUNDGR I.Improved empty freight car distribution［J］.Transportation Science，1998，32（22）：163～1736.

［5］韩晓龙，张盟学.集装箱空箱调运优化模型［J］.集美大学学报，2013（3）：114－118.

［6］胡晓龙.集装箱空箱调运优化的模型与方法研究［D］.南京：东南大学，2005.

［7］施 欣.集装箱海运空箱调运优化分析［J］.系统工程理论与实践，2003，4（4）：70－76.

［8］周红梅，方 芳.航运集装箱空箱调运优化模型的研究［J］.武汉理工大学学报，2003（6）：384－387.

［9］SHEN W S，KHONG C M.A DSS for empty container distribution planning［J］.Decision Support System，1995，15（l）：75－82.

［10］彭守民，王 妍.多式联运下集装箱空箱调运问题分析［J］.中国水运，2011（6）：29－30.

［11］SOOK T C，MICHAEL H C，ERHAN K.Empty container management for intermodaltransportation networks［J］.Transportation Research Part E，2002，38：423－438.

［12］张维迎.博弈论与信息经济学［M］.上海：格致出版社，2004.