二维潜艇流水孔空腔减阻数值研究＊

熊鳌魁 仲 夏 包胜平 刘艾明

（武汉理工大学交通学院 武汉 430063）

0 引 言

潜艇靠改变自身重量来实现下潜上浮，它有多个蓄水仓，当潜艇要下潜时就往蓄水舱中注水，使潜艇重量增加，大于它的排水量，潜艇就下潜；要上浮时就往外排水，使潜艇重量降低，小于它的排水量，潜艇就上浮.因此在采用双壳体结构潜艇的非水密非耐压艇体上，必须开设一些不受控的自由流水孔，这样当潜艇处于水下状态时，可以保证非水密非耐压艇体处于自由浸水状态.流水孔的位置一般在潜艇的中部，尺寸较大，十分醒目.流水孔的数量和尺寸会影响到潜艇在水下航行的阻力.流体力学的计算和试验结果均表明，当潜艇处于水下航行状态时，艇体上一个流水孔的阻力是同样尺寸平板的4～5倍.一艘潜艇的流水孔数量过多、尺寸过大，将会增加水下航行的阻力，直接导致水下航速降低.

由于潜艇用于军事居多，因此国内外的相关资料都处于保密状态.在非保密的水下航行器历史上利用流水孔置翼的方法达到减阻目的的研究较少.相关减阻主要有：Li Yunbo等［1］通过空气腔减少船舶阻力，且空气腔的形成受空化数、速度、槽的几何形状和槽的尺寸影响；黄微波［2］通过喷涂聚脲柔性涂层达到减阻目的，在柔性脂肪层表面喷涂聚脲柔性表皮减阻层，形成一种含有不同性能、结构的复合柔性减阻层，模拟海豚的表皮及皮下脂肪结构在水中的减阻作用。经测试，在水流速度为4m／s时，柔性表皮减阻层达到12%～15%的减阻效果。在水流速度为3～10m／s范围内，复合柔性减阻层平均减阻率为6.84%；李慧明［3］指出纵向沟空腔只在湍流状态时起减阻作用，横向沟空腔在湍流和层流状态时都能起到减阻作用，微气泡减阻只对湍流起减阻作用，微气泡在近壁区的缓冲层内时起到的减阻作用最佳；郝英泽等［4］认为尽可能减少艇体表面开孔数量和开孔面积，并在流水孔内安装阻流板或将流水孔装上自动启闭装置，但由于启闭装置的维护艰难，这种方法遭淘汰.还有一些国家采用了另外较为简单的解决办法，如在流水孔处装设固定式的扁平条格栅结构，格栅中的扁平条方向与水流方向垂直或成某一角度.本文在于由于流水孔空腔相对于平板而言摩擦阻力减小、压差阻力增大，并产生漩涡回流，通过放置机翼达到影响流场减小压差阻力，并利用升力原理通过漩涡回流产生负阻力，从而使总阻力减小，提高潜艇的航行速度.

1 研究方法与步骤

1.1 物理模型

采用基于ANSYS的DM建模工具和CAD建模软件结合起来构建了二维的平板、流水孔空腔以及流水孔空腔内放置机翼（简称流水孔空腔置翼）3种模型.平板长10m，中部是简化后的正方形流水孔空腔，边长为1m，流水孔是外部流体与潜艇内部空腔连接的通道，内部潜艇空腔简化为长4m、高3m的长方形空腔.机翼弦长为0.182m.为了模拟深水海域，平板以下流体区域取10m深，如图1，2所示.计算采用的机翼是NACA－4212机型，机翼纵剖面图及参数如图2、表1.

图1 流水孔空腔置翼模型示意图

图2 NACA－4212机翼剖面形状

表1 机翼参数

1.2 网格划分

对于在求解域内建立的偏微分方程，通常不能直接解出.必须将空间离散成很小的单元，通过许多个有限空间离散点来代替原始的连续空间，在计算机软件中被称为网格划分.在前处理模块Mesh中采用非结构化网格对流动区域进行网格划分，并在机翼附近流动复杂区域加密，合理分布网格.如图3.

1.3 数值模拟

图3 流水孔空腔置翼模型网格图

采用雷诺时均N－S方程数值方法，即将N－S方程对某一时间尺度取平均得到RANS方程，再对引入湍流模式后构成的封闭方程组求解得到湍流要素的时均值.对于所有的流动，FLUENT都要解质量守恒方程和动量守恒方程.通过动量守恒定律可以得到粘性不可压缩流体的N－S［5］方程表达式为

应用雷诺时均值计算法则，可以得到RANS方程和雷诺时均连续性方程［6］

式中：ui为笛卡尔坐标系中xi方向的速度分量（j＝1，2，3）；p为流体压力；ρ为流体密度；v为流体运动粘性系数；fi为体积力.

FLUENT［7］求解过程中，控制方程为流体计算的核心方程N－S，采用标准k－ε湍流模型，入口边界条件为velocity－inlet，模拟潜艇速度35kn，约18m／s，水粘性系数ν为1×10－6m2／s；出口设为outflow.近壁面为标准壁函数（standard wall functions），使用有限体积法进行离散.方程如下.

式中：Gk为由平均速度引起的湍动能；Gb为由用于浮力影响引起的湍动能；Ym为湍流脉动膨胀对总的耗散率的影响.

2 计算结果分析

2.1 平板模型数值模拟结果验证数值模拟可靠性

为验证精度，将数值模拟结果与平板经验公式进行比较，如图4所示.其中，经验公式选取了尾流定律式［8］

由图4可见，数值模拟的平板摩擦阻力系数与经验公式计算的摩擦阻力系数分布情况基本一致，说明该软件能较好的模拟实际阻力系数值，其结果有效可靠.在平板前部有较小偏差，原因可能是：（1）数值计算中来流设有湍流度；（2）数值计算中的平板前缘的速度分布是均匀的.

图4 平板模型阻力系数分布和经验公式比较图

2.2 流水孔空腔模型数值模拟结果

图5，6为流水孔空腔模型的速度云图及压力曲线图.由图5，6中可见，流水孔内部的速度减小，形成回流.流水孔内圈比外圈的速度更小，流水孔后部形成高压区、前部形成低压区，产生压差阻力.

尤其是在节假日，车队的拖车费用，船公司的海运费，航空公司的空运费用，港口码头的港杂费、堆存费、落箱费等包干费都会水涨船高，使得HM公司的实际报价比与客户签订合同时的报价高，导致部分的客户会因此对HM国际货代公司有所不满。

图5 流水孔空腔模型的速度云图

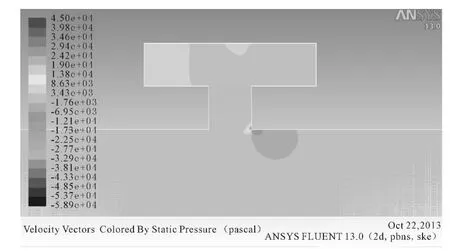
图6 流水孔空腔模型的压力曲线图

2.3 空腔置翼模型数值模拟结果

以正方形流水孔空腔底边中心处为坐标原点（见图 7），加入的机翼的坐标位置为 （0.45，0.12），拱度朝下，以x正半轴为参考线逆时针旋转60°，并将流水孔后部改成半径为0.2的圆弧流线型.图8为空腔置翼模型的速度云图.由图8可见，机翼对流体的速度有所影响，但总体的速度分布趋势仍不变.流水孔内仍为外圈速度大于内圈.

图7 坐标轴原点位置图

图8 空腔置翼模型的速度云图

在空腔置翼模型中，保持水的密度、粘度、来流以及空腔的尺度不变.如图9为空腔置翼模型的压力云图.由图9可见，机翼放置后利用了在流水孔后部形成的高压区，利用翼升原理产生垂直于漩涡来流的升力，该升力在x轴方向的分量为负，即相对于潜艇而言为推力.同时机翼与流线型的共同作用使原来湍流较大的流水孔后部的湍流度减小，干扰了流水孔空腔内的漩涡压力场，使流水孔空腔内的压差阻力减小.由于机翼的放置，平板前部的压力分布变得均匀，平板后部的压力分布减小.

图9 空腔置翼模型的压力云图

2.4 摩擦阻力分析

2种模型摩擦阻力对比见表2.

表2 2种模型摩擦阻力对比表 N

由表2可见，空腔模型相对于空腔置翼模型摩擦阻力减小，这是因为机翼放置后，不仅空腔内漩涡减小，平板前后部的湍流度也相应减小，导致总摩擦阻力减小.在流水孔与空腔位置上，由于空腔内产生漩涡回流，回流的方向与来流方向相反，导致空腔内摩擦阻力为负值，加入机翼后，由于机翼尺寸小，所以机翼上的摩擦阻力较小.

2.5 压差阻力分析

2种模型压差阻力对比见表3.

由表3可见，空腔模型中平板前后部的压差阻力可忽略不计，此时压差阻力主要集中在流水孔与空腔处.流水孔内加入机翼后，对流水孔与空腔内的压力场有所干扰，同时机翼的前后面利用压差产生了有效的推力，抵消了一部分压差阻力.此外，流水孔尾部用流线型代替直角型，使本身存在的压力突增也减小许多.因此，总压差阻力基本维持不变.

表3 两种模型压差阻力对比表 N

2.6 总阻力分析

表4 船底平板模型总阻力对比表 N

综合以上3组表格分析得出，空腔置翼模型相对于空腔模型而言，摩擦阻力减小，压差阻力不变，总阻力减小.说明空腔置翼模型相对于空腔模型而言确实有减阻效果.根据减阻率计算公式f＝（空腔模型总阻力－空腔置翼模型总阻力）／空腔模型总阻力，可初步得出该数值模拟模型的减阻率为4.23%.但由于该数值模拟建立在二维模型上，即默认宽度方向上的尺寸均为1m，所以三维机翼的加入方式以及实际流水孔空腔模型的尺寸会影响实际减阻率的大小.更为精确的三维模型减阻效果的检验和实验检验还有待展开.

3 结 论

1）通过将潜艇壁面流水孔简化为二维空腔模型进行数值模拟可以看出空腔内产生漩涡回流.利用漩涡回流和升力原理在空腔内加入机翼可以产生负阻力，达到减阻效果.

2）机翼的放置与流水孔后部角隅处线型的改善使原始的流水孔空腔摩擦阻力减小、压差阻力几乎不变，总阻力有所下降.

3）通过对二维模型的数值模拟能初步判断该模型的减阻率约为4.23%.

在初步探索空腔置翼模型对潜艇流水孔空腔模型周围流场的改变及其减阻机理的影响基础上，今后可在以下方面继续探索：（1）因计算机条件所限，计算精度、流场信息、各项参数分布有待进一步提高和改善；（2）所获得的数值计算结果需与实验结果进行比较分析，计算精度还有待于通过物理实验进行验证；（3）研究的模型都指定来流速度为5m／s，但在不同来流速度下，漩涡的大小形状以及潜艇边界层的厚度和紊流的出现位置都将发生改变；给该减阻模型留下很大的研究空间；（4）进行的数值模拟是建立在二维模型基础上.但模型宽度及开空腔尺度对减阻率有一定影响.所以更为实际的三维模型也是今后的研究方向之一.

［1］LI Yunbo，WU Xiaoyu，MA Yong，et al.A method based on potential theory for calculating air cavity formation of an air cavity resistance reduction ship［J］.Journal of Marine Science and Application，2008，2：98－101.

［2］黄微波.水下航行器喷涂聚脲柔性涂层的制备及减阻性能的研究［D］.青岛：中国海洋大学，2007.

［3］李慧明.水下航行器减阻技术数值模拟及机理分析［D］.哈尔滨：哈尔滨工业大学，2006.

［4］郝英泽，林凡彩，刘百顺.浅析潜艇水下航行阻力及减阻措施［C］∥2009特大型船舶操纵和船舶安全与管理论文集，中国航海学会海洋船舶驾驶专业委员会，2009：4.

［5］熊俊涛，乔志德，韩忠华.基于 Navier－Stokes方程跨声速翼型和机翼气动优化设计［J］.空气动力学学报，2007（1）：29－33.

［6］王家楣，张志宏，马乾初，流体力学［M］.大连：大连海事大学出版社，2002.

［7］韩占忠，王 敬，兰小平.FLUNET流体工程仿真计算实例与应用［M］.北京：北京理工大学出版社，2004.

［8］生进武文，井上雅弘.粘性流体力学［M］.北京：海洋出版社，1984.