一类p（x）-Lap lacian问题解的存在性

高娟娟，贾小尧，马继佳

（河南科技大学数学与统计学院，河南洛阳471023）

0 引言

近年来，具有变指数增长条件的偏微分方程理论在弹性力学、电子流变流体学以及图像处理等方面变得越来越重要。变指数空间问题最早由波兰数学家W.Orlicz提出，而后由捷克数学家O.Kovácˇik和J.Rákosn′ik系统地建立［1］。从此以后，变指数空间的基本理论研究［2－4］以及具有变指数增长条件的偏微分方程的研究［5－13］吸引了国内外广大学者的关注，其中，文献［5－9］研究了具有Dirichlet边界条件的变指数问题，文献［10－13］讨论了具有Neumann边界条件的变指数问题。但是，这些文献都是关于次临界或者临界情形的研究，对于具有超临界增长指数的变指数问题的研究则较少［14－15］。本文讨论一类具p（x）-Lap lacian算子且带有超临界非线性项的Dirichlet问题：

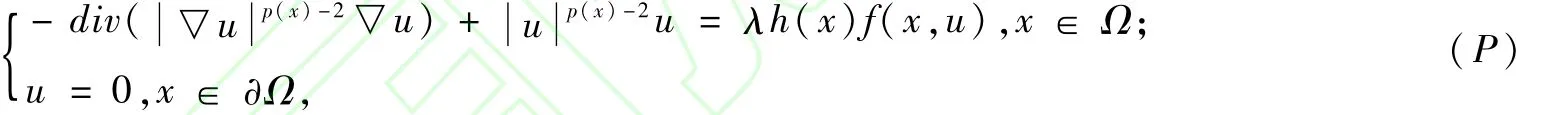
其中，Ω⊂RN是一个具有柱对称性的有界正则区域；p（x）∈C（），1＜p（x）＜N，∀x∈，且λ＞0。本文利用一个新的紧嵌入定理以及经典的变分方法得到了问题（P）弱解的存在性。

1 预备知识

本节将介绍有关变指数空间Lp（x）（Ω）和W1，p（x）（Ω）的相关结论，详细内容见文献［1－4］。

令Ω＝Ω1×Ω2⊂RN，其中Ω1⊂Rm（m≥1）是有界正则区域，Ω2⊂Rk（k≥2）是中心在原点半径为R的球。定义：

假设h（x）满足以下条件：（h1）：h（x）是上的非负Hölder连续函数，关于x2∈Ω2径向对称且满足h（x1，0）＝0；（h2）：lh＞0，lh＝sup｛λ＞0：＜∞，x∈Ω｝。

定义：

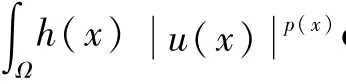
命题3 假设h（x）满足条件（h1），（h2），且p（x），q（x）∈C＋（）∩S（Ω），p（x）＜N，则存在一个常数τ＞0，使得当p（x）＜q（x）＜p*（x）＋τ时（p*（x）＝为临界指数），嵌入W（Ω）→（Ω）是紧的。

且有以下结论：

（1）L是连续有界且严格单调的算子；

（2）L是（S＋）型映射，即若在W1，p（x）（Ω）中有unu，且p（L（un）－L（u），un－u）≤0，则un→u。

命题5 记Φ＝∫ΩλF（x，u）d x，则若unu就有Φ（un）→Φ（u）和Φ′（un）→Φ′（u）。

2 主要结果

下面，给出f（x，t）的假设条件：

（f1） f：Ω×R→R满足Caratheodory条件，且存在两个常数C1，C2＞0使得≤C1＋C2q（x）－1，∀（x，t）∈Ω×R，其中，q（x）∈C＋（Ω），q（x）＜p*（x）＋τ（τ＞0是命题3中得到的常数）。

（f2） ∃M＞0，θ＞p＋，使得0＜θF（x，t）＜f（x，t）t对于≥M，∀x∈Ω成立，其中F（x，t）＝（x，s）d s。

（f3） f（x，t）＝o（p＋－1），t→0对于x∈Ω是一致的。

定理1 若f（x，t）满足条件（f1）且q＋＜p－，则问题（P）有一个弱解。

证明 根据条件f1有≤C（1＋q（x）），∀（x，t）∈Ω×R。令＞1，可得：

因为q＋＜p－，所以当→∞时有I（u）→∞，即I是强制的。由命题3可知，I是弱下半连续泛函。从而，I在W（Ω）中有一个极小值点u，即为问题（P）的一个弱解。

定义2 （（PS）条件）称一个C1的泛函Φ：Χ→R满足（PS）条件，如果任意一个在X中使得有界且Φ′（vk）→0的序列｛vk｝（称为（PS）序列）都有收敛子列。

定理2 假设f（x，t）满足条件（f1）、（f2），并且条件（h1）、（h2）成立，则I满足（PS）条件。

证明 设｛un｝⊂W（Ω）是（PS）序列，即｛I（un）｝有界且当n→∞时有→0。接下来需要证明｛un｝有收敛子列。

由θ＞p＋可知｛un｝是有界的。因为W（Ω）是自反的Banach空间，所以可以找到一个弱收敛子列｛uni｝⊂W（Ω）。由于uniu且I′（uni）→0，应用命题4和命题5可知uni→u。选择｛unj｝⊂｛uni｝使unj∈S（Ω），因此｛unj｝⊂W（Ω）且仍有unj→u。从而，I满足（PS）条件。

定理3 若f（x，t）满足条件（f1）～（f3），h（x）满足条件（h1）和（h2），且q－＞p＋，则问题（P）有一个非平凡的弱解。

证明 下面利用山路引理证明。由定理2可知I满足（PS）条件。因为p＋＜q－≤q（x）＜p*（x）＋τ，∀x∈Ω，有以下紧嵌入结果：

从而，存在常数C0，C1，

根据条件（f1）和（f3）可知，存在任意常数0＜ε＜1和常数C（ε）＞0，使得

令ε＞0足够小，使得0＜λεC0＜，从而有

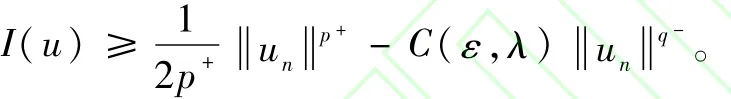
因为q－＞p＋，所以必存在r＞0和δ＞0，使对每个u∈W（Ω）且＝r都有I（u）≥δ＞0成立。

于是，当t→＋∞时，有I（tv）→－∞。又因I（0）＝0，从而I满足了山路引理的条件。因此泛函I至少有一个非平凡的临界点。

［1］ Kovácˇik O，Rákosn′ik J.On Spaces Lp（x）（Ω）and Wk，p（x）（Ω）［J］.Czechoslovak Math J，1991，41（116）：592－618.

［2］ Fan X L，Zhao D.On the Spaces Lp（x）（Ω）and Wm，p（x）（Ω）［J］.JMath Anal Appl，2001，263：424－446.

［3］ Fan X L，Shen JS，Zhao D.Sobolev Embedding Theorems for Spaces Wk，p（x）（Ω）［J］.JMath Anal Appl，2001，262：749－760.

［4］ Gao J J，Zhao P H，Zhang Y.Compact Sobolev Embedding Theorems Involving Symmetry and Its Application［J］.Nonlinear Differ Equ Appl，2010，17：161－180.

［5］ Chabrowski J，Fu Y Q.Existence of Solutions for p（x）-Lap lacian Problems on a Bounded Domain［J］.JMath Anal Appl，2005，306：604－618.

［6］ Fan X L.On the Sub-supsolution Method for p（x）-Laplacian Equations［J］.JMath Anal App l，2007，330：665－682.

［7］ Mayte P L A，Julio D R.The Limit as p（x）→∞of Solutions to the Inhomogen-eous Dirichlet Problem of the p（x）-Laplacian［J］.Nonlinear Anal，2010，73：2027－2035.

［8］ Zhang Q H.Existence of Positive Solutions to a Class of p（x）-Laplacian Equations with Singular Nonlinearities［J］.Applied Mathematics Letters，2012，25：2381－2384.

［9］ Ghaemia M B，Afrouzi B G A，Rasouli C S H，et al.On the Existence of Positive Solutions for a Class of（p（x），q（x））-Laplacian System［J］.Applied Mathematics Letters，2013，26：367－372.

［10］ M ihaˇilescu M.Existence and Multiplicity of Solutions for a Neumann Problem Involving the p（x）-Lap lace Operator［J］.Nonlinear Anal，2007，67：1419－1425.

［11］ Fan X L，Ji C.Existence of Infinitely Many Solutions for a Neumann Problem Involving the p（x）-Lap lacian［J］.JMath Anal Appl，2007，334：248－260.

［12］ Deng S G，Wang Q.Nonexistence，Existence and Multiplicity of Positive Solutions to the p（x）-Laplacian Nonlinear Neumann Boundary Value Problem［J］.Nonlinear Anal，2010，73：2170－2183.

［13］ Cammaroto F，Vilasi L.On a Perturbed p（x）-Laplacian Problem in Bounded and Unbounded Comains［J］.JMath Anal Appl，2013，402：71－83.

［14］ Yao JH，Wang X Y.On an Open Problem Involving the p（x）-Laplacian-A Further Study on the Multiplicity of Weak Solutions to p（x）-Laplacian Equations［J］.Non Anal，2008，69：1445－1453.

［15］ Dimitrios A K，Nikolaos S.Elliptic Problems Involving the p（x）-Laplacian with Competing Nonlinearities［J］.JMath Anal Appl，2011，379：378－387.