主动悬架的H2／H∞混合输出反馈控制

胡爱军，孔令强

（河南理工大学机械与动力工程学院，河南焦作 454000）

主动悬架的H2／H∞混合输出反馈控制

胡爱军，孔令强

（河南理工大学机械与动力工程学院，河南焦作 454000）

运用线性分式变换建立了包含不确定参数的半车悬架系统模型，选择合适的性能加权函数得广义被控对象。为了保证不确定参数具有鲁棒稳定性，用H∞范数作为参数不确定性的性能指标，同时，为了使悬架系统性能指标处于一个好的水平，用H2范数作为衡量扰动作用下悬架性能指标，设计了H2／H∞混合控制器。在M talab7.0／Simulink环境下搭建仿真模型完成对系统的仿真分析。仿真结果证明：主动悬架的乘坐舒适性明显优于被动悬架的乘坐舒适性，同时汽车的操作稳定性也有一定程度的改善。

主动悬架；不确定性；鲁棒控制；仿真

0 引言

汽车悬架系统是现代汽车的重要组成部分，对汽车的行驶平顺性以及操作稳定性等性能指标有着重要的影响。目前，人们对悬架的设计开发工作主要集中在对控制策略的研究方面，如遗传算法、滑模控制、模糊控制等［1－3］。这些算法一般没有考虑模型的不确定性问题，实际上悬架系统存在诸多不确定的因素，比如汽车簧载质量、轮胎刚度［4］等因素都会产生一些变动。文献［5］建立了考虑高阶未建模不确定性的汽车悬架模型，设计了H2／H∞混合控制器，一定程度上提高了悬架模型的精度，但高阶未建模不确定性对模型不确定性的描述不够精确，所建的模型过于简单，很多性能不能表达出来。文献［6］应用硬约束、H2性能、H∞性能以及极点配置等多约束设计了主动悬架H2／H∞混合控制器，但没有考虑模型的不确定性问题。为了能够准确表达悬架模型的不确定性，本文运用线性分式变换（LFT）建立了包含不确定参数的主动悬架LFT模型，同时为了体现更多悬架性能建立了1／2车体悬架模型。汽车悬架设计时应考虑乘坐舒适性、操作稳定性以及机械约束3项指标［7］，而乘坐舒适性主要取决于悬架的垂向加速度、俯仰角加速度和悬架动挠度，操作稳定性取决于前后轮胎的动载荷。为了使悬架系统性能指标处于一个好的水平，本文用H2范数作为衡量扰动作用下悬架性能指标，同时为了保证不确定参数具有鲁棒稳定性，用H∞范数作为参数不确定性的性能指标，运用线性矩阵不等式方法（LMI）设计H2／H∞混合控制器。

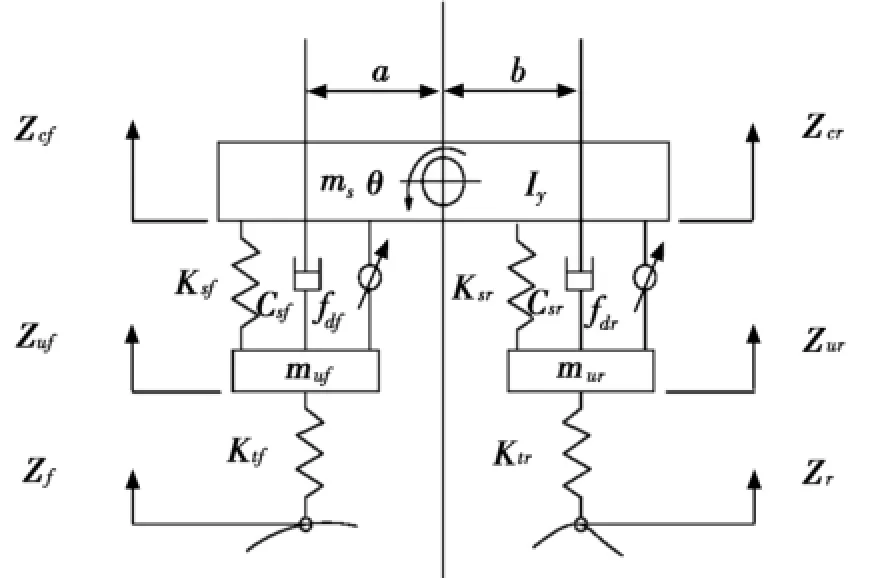
图1 半车主动悬架系统模型

1 半车悬架模型及不确定性描述

图1为半车主动悬架系统模型。在图1中，ms和Iy分别表示悬架簧载质量和簧载质量转动惯量；Zcf、Zcr和Zuf、Zur分别表示前、后悬架簧载质量和非簧载质量位移；Zf和Zr分别表示前、后路面位移；Ksf、Ksr分别表示前、后悬架刚度；Csf、Csr分别表示前、后悬架阻尼系数；Ktf、Ktr分别表示前、后轮胎的刚度系数；fdf、fdr分别表示前、后悬可控库仑力；a和b表示前后悬架到质心的距离；θ表示悬架的俯仰角度。

根据悬架模型建立如下微分方程：

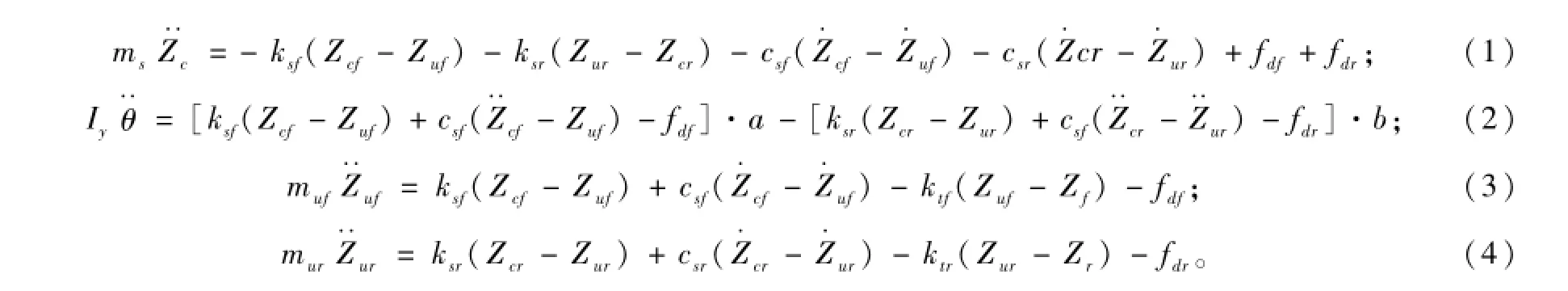
当俯仰角θ在小范围变动时，近似有：

簧载质量会随着汽车载货或载人多少而产生一些变化，轮胎刚度也会随着轮胎使用时间的长短以及轮胎充气量多少而变化。实际的质量ms在公称质量的30%范围内变化，实际轮胎的刚度kt在公称刚度的20%范围内变化。这里采用乘性不确定表示参数的不确定性，即：

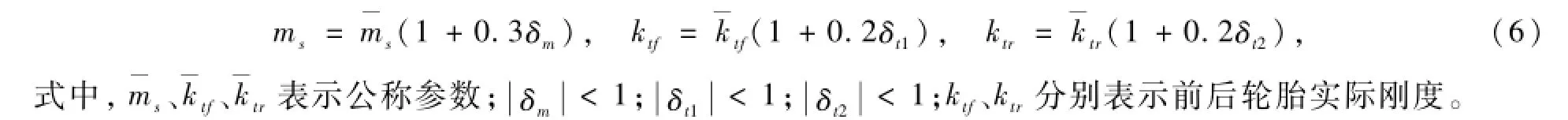
图2 不确定模型框图

2 混合H2／H∞控制器设计

2.1 广义被控对象的描述

根据ISO2631—1997标准，人体对振动的敏感频率范围在垂直方向为4～8 Hz，在旋转方向为1～2 Hz。取垂直方向和俯仰方向加权传递函数分别为：

为了保证悬架动行程不超过其物理限制，选择W3（s）为这一输出的频率加权函数：

广义被控对象的控制框图如图3所示。

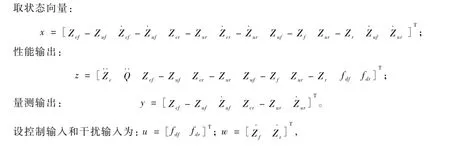
图3 广义被控对象的控制框图

可得广义被控对象的状态空间方程为：

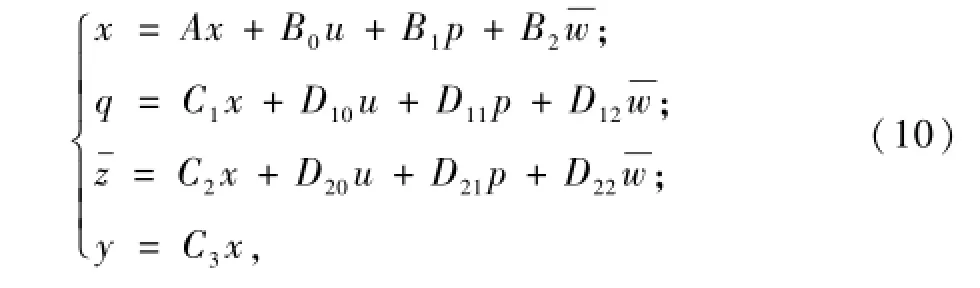
式中，A、B0、B1、B2、C1、D10、D11、C2、D20、C3均为定常矩阵；D12、D21、D22为零矩阵。

2.2 控制器的设计

设计一个u＝Ky输出反馈的控制器，使得闭环系统是渐近稳定的，且从p到q的闭环传递函数Tpq的H∞范数不超过一个给定的上界，以保证闭环系统对由p＝△q进入的不确定性具有鲁棒稳定性；同时使得从到z的闭环传递函数的H2范数尽可能小，以保证用H2范数度量的系统性能处于一个好的水平。即满足：

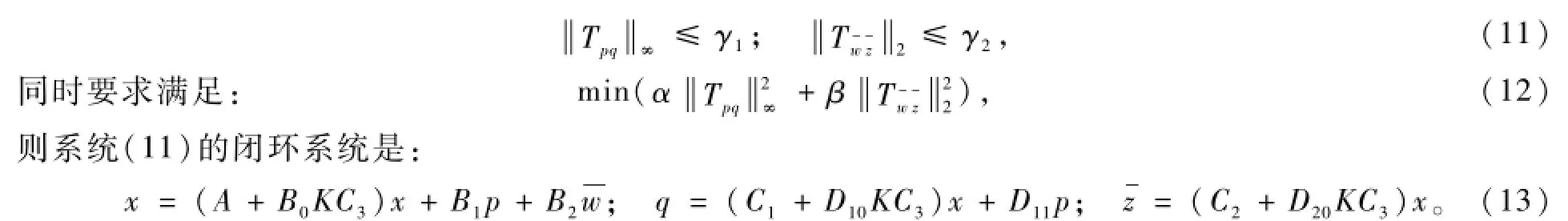
根据文献［9］可得，要求闭环系统（13）具有性能（11），当且仅当存在对称正定矩阵X1和X2，使得如下不等式成立：

为了能够求解上述不等式，需引进一个附加约束，即：X＝X1＝X2，应用变量替换的方法，令W＝KC3X，则可把上述非线性不等式问题转化为线性矩阵不等式：

运用求解器mincx求解上述矩阵不等式可得最优解X和W，有K＝W（C3X）－1。

3 仿真与分析

车辆参数为：ms＝690 kg；Iy＝1 222 kg·m2；muf＝mur＝192 kg；ksf＝17 kN／m；ksr＝22 kN／m；ktf＝ktr＝192 kN／m；csf＝csr＝1.5 kN·s／m；a＝1.25 m；b＝1.51 m。选择积分白噪声路面模型作为激励信号运算得到H∞的性能指标为0.479 78，H2的性能指标为0.240 91，所得控制器

在Matlab7.0环境下，对采用所设计控制器的主动悬架进行仿真，并与被动悬架进行对比，绘制出车身垂向加速度、俯仰角加速度、轮胎变形量以及悬架动挠度的幅频特性曲线，如图4～图7所示。由图4可知：在质心的垂向加速度方面，采用所设计控制器的主动悬架明显优于被动悬架，在频率为4～8 Hz时性能得到明显的改善。由图5可知：在悬架的俯仰角加速度方面，采用所设计控制器的主动悬架比被动悬架有所减小，在频率为人体敏感的1～2 Hz时得到明显的改善，这说明汽车的乘坐舒适性得到提高。由图6可知：主动悬架在高频段的轮胎变形量有一定恶化。由图7可知：在小于1 Hz的范围内悬架动挠度有一定恶化，这是悬架系统的固有特性，性能指标之间存在制约关系所致。

图4 垂向加速度的幅频特性

图5 俯仰角加速度幅频特性

图6 轮胎变形量的幅频特性

图7 悬架动挠度的幅频特性

假设汽车以速度u＝30 m／s行驶在C级路面上，在Matlab7.0／Simulink中搭建汽车模型，仿真得到汽车在时域范围内的响应曲线，如图8～图13所示。

图8 垂向加速度响应

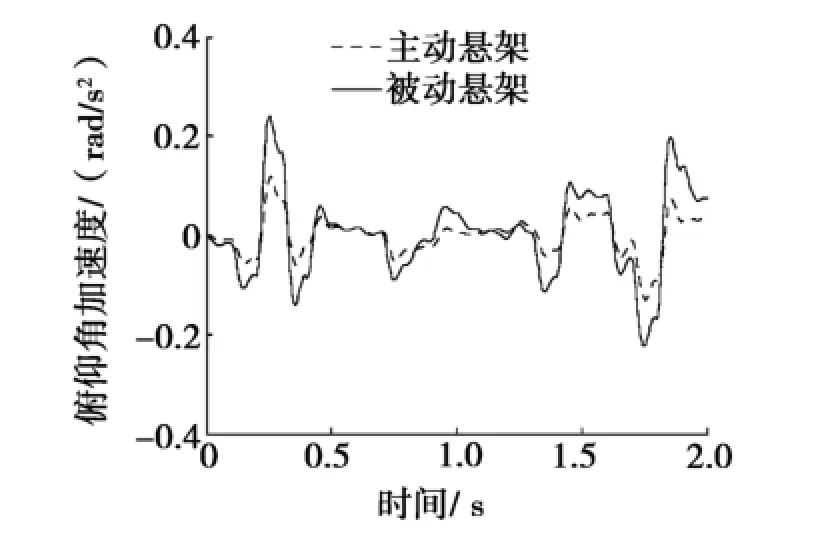
图9 俯仰角加速度响应

在图8中，主动悬架的垂向加速度的峰值明显低于被动悬架，垂向加速度最高峰值减低约28%。在图9中，主动悬架的俯仰角加速度的峰值也明显降低，最高峰值减低约50%，这说明主动悬架的乘坐舒适性得到改善。

图10 后悬架动行程

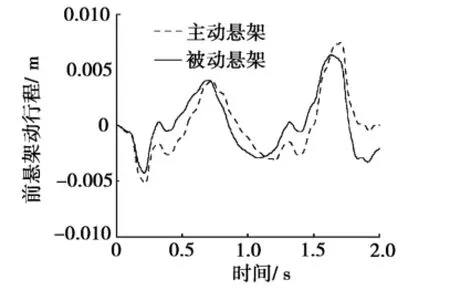
图11 前悬架动行程

图12 前轮轮胎变形量

图13 后轮轮胎变形量

在图10和图11中，主动悬架的悬架动行程比被动悬架有所增加，但增加幅度很小，只要保证在机械约束的范围内，不影响乘坐舒适性。对图12和图13比较可知：主动悬架比被动悬架的轮胎变形量略有减小，这在一定程度上提高了汽车的操作稳定性。

4 结论

运用LFT建立含有不确定参数主动悬架的LFT模型，设计了H2／H∞混合控制。利用Matlab7.0／Simulink进行了频域和时域范围内的仿真分析。通过仿真结果证明所设计的控制器是有效的。采用所设计控制器以后，主动悬架的乘坐舒适性明显优于被动悬架的乘坐舒适性，同时，汽车的操作稳定性也有一定程度的改善。

［1］ 龚侃，何天明，陈超.基于遗传算法的汽车悬架仿真与优化设计［J］.武汉理工大学学报，2012，34（3）：313－316.

［2］ 韩卫沙，张京军.基于滑模控制的半主动悬架系统仿真分析［J］.西华大学学报，2011，30（2）：43－46.

［3］ 杨博，赵江杰，郭志军.铰接式自卸汽车平衡悬架动力学特性［J］.河南科技大学学报：自然科学版，2012，33（2）：22－25.

［4］ Damine SO S，Luc D.Skyhook and H∞Control of Semi-active Suspension：Some Practical Aspercts［J］.Vehicle System Dymamics，2003（4）：273－308.

［5］ 方敏，史明光，陈无畏.汽车主动悬架多目标H2／H∞混合控制［J］.农业机械学报，2005，36（3）：5－7.

［6］ 徐伯林，贾英民.多约束主动悬架H2／H∞混合控制设计［J］.计算机仿真，2012，29（3）：44－48.

［7］ Hrovat D.Survey of Advanced Suspension Developments and Related Op timal Control Applications［J］.Automatica，1997，33（10）：1781－1817.

［8］ 周克敏，Doyle JC，Glover K.鲁棒与最优控制［M］.北京：国防工业出版社，2002.

［9］ 俞立.鲁棒控制—线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002.

［10］ 喻凡，林逸.汽车系统动力学［M］.北京：机械工业出版社，2005.

U461.4

A

1672－6871（2014）03－0027－05

国家自然科学基金项目（U1204517）；河南省教育厅自然科学研究计划基金项目（2011A460006）；河南理工大学博士基金项目（B2009－16）

胡爱军（1974－），男，河南焦作人，讲师，博士，硕士生导师，研究方向为汽车系统动力学与控制.

2013－09－04