一种基于圆形分布的支撑向量机核选择方法

郭金玲

（山西大学商务学院，山西太原 030031）

一种基于圆形分布的支撑向量机核选择方法

郭金玲

（山西大学商务学院，山西太原 030031）

针对目前支撑向量机核函数的选择没有统一规则的现状，提出了一种结合数据分布特征进行支撑向量机核选择的方法。首先，采用多维尺度分析方法对高维数据集合理降维，提出判断数据集是否呈圆形分布的算法，在得到数据集分布特征的基础上进行核选择，达到结合数据分布特征合理选择支撑向量机核函数的目的。实验结果表明：呈圆形分布的数据集采用极坐标核进行分类，识别率达到100%，训练时间短，优于采用神经网络、决策树、高斯核及多项式核的分类效果。该方法提高了支撑向量机的泛化能力。

支撑向量机；核选择；圆形分布；极坐标

0 引言

支撑向量机（SVM）是一种基于统计学习理论的学习方法［1］，主要被用来解决数据的回归与分类问题。在使用SVM进行回归或分类时常用的核函数有高斯核、多项式核构造SVM最重要的一个问题是SVM核的正确选择，因此，目前SVM的一个重要研究内容就是如何有效进行核函数的选择。

在采用SVM处理数据分类问题时，基于数据依赖的SVM核函数选择方法［5－8］主要是在SVM训练之前对核及参数进行优化处理。如文献［7－8］提出的极小化R2／△2的核选择方法、两步迭代法等。基于数据独立的SVM核函数选择方法［9－10］主要利用有关问题的先验信息进行SVM核函数选择，代表性的方法有留一交叉校验法［9］等。数据依赖的方法具有通用性，但泛化能力差。数据独立的方法计算代价太大，一般只作为参考。

在现有的方法中，很少利用到数据集中包含的几何分布信息，本文提出一种结合数据集几何分布特征进行核选择的方法，通过数值实验，验证了该方法可以降低计算代价，分类效果较好，直观性较强。

1 基于圆形分布的支撑向量机核选择方法

设实验数据集包含两类样本，分别是A类样本和B类样本。基于圆形分布的SVM核选择方法具体过程如下：

步骤1：实际问题中大多都是高维数据集，可首先对数据集进行降维处理。多维尺度分析方法（MDS）［11］是把原来多个变量划为少数几个综合指标的降维处理方法，是较好的一种线性降维方法，首先采用该方法对高维数据集进行降维，处理成二维数据集。

步骤2：设A类样本的重心为O，A类样本各点到O的距离计为数组dA，B类样本各点到O的距离计为数组dB。两个数组中的最大值分别记为dAmax和dBmax；最小值分别记为dAmin和dBmin。判断dAmax＜dBmin或dBmax＜dAmin是否成立，如果成立，可以判定该数据集呈圆形分布。

步骤3：结合样本集的分布选择相应的核函数，样本集呈圆形分布，相应的SVM选择极坐标核；反之，选择常用的高斯核或多项式核。

2 实验与分析

2.1 数值实验

为验证基于圆形分布的SVM核选择方法是否有效，分别采用4组数据在Matlab环境中进行数值实验，并对实验结果进行了分析。

其中，第1组实验数据为人工构造的圆形数据集D1。数据集D1包含两类样本，A类样本满足条件x2＋y2≤1，用圆圈表示；B类样本满足条件x2＋y2＞1，用‘*’表示，随机生成100个样本，其分布如图1所示。

第2组数据集D2采用了鸢尾植物数据集Iris.data，该数据集包括70个训练样本，30个测试样本，每个样本有5个属性。由于数据集D2为高维数据集，首先使用MDS方法对D2进行降维，降维后得到的数据集E1的分布情况如图2所示。

图1 数据集D1的分布情况

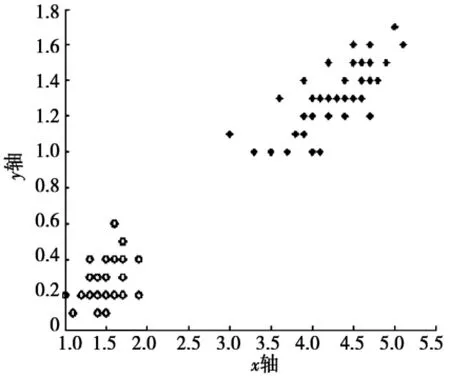
图2 数据集D2的分布情况

第3组真实数据集D3是一个呈双正弦线分布的二维数据集，分类要求是把x-y坐标平面上两条不同正弦线上的点正确的分开，由于正弦分布是呈周期变化的，所以实验中取了4个周期的点。数据分布如图3所示，圆圈和“*”分别代表不同的正弦线，每类120个采样点，每个样本点有两个属性。

第4组数据集D4是一个随机生成的基本呈均匀分布的二维数据集，样本数为50，其分布如图4所示。

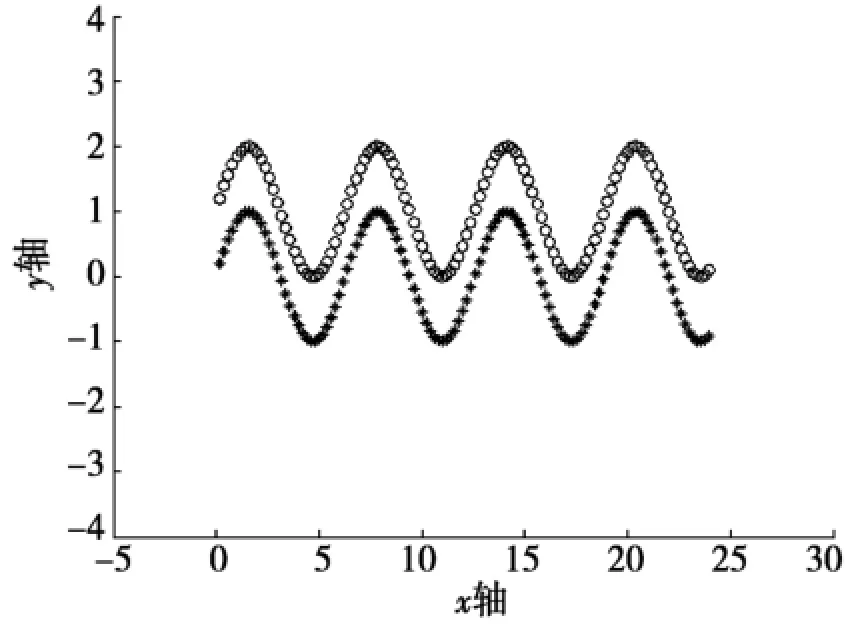
图3 4个周期的双正弦线

图4 数据集D4的分布情况

采用文中提出的算法对数据集D1、D2、D3、D4进行检测，可得出结论：D1、D2、D3呈圆形分布，D4不呈圆形分布。分别采用神经网络方法（NN）［12］、决策树方法［13］、极坐标核SVM、高斯核SVM、多项式核SVM对4组数据集进行了分类实验，分别进行了12次数值实验，取平均结果作为最后结果。

采用不同方法对D1、D2、D3、D4进行分类的结果具体见表1。

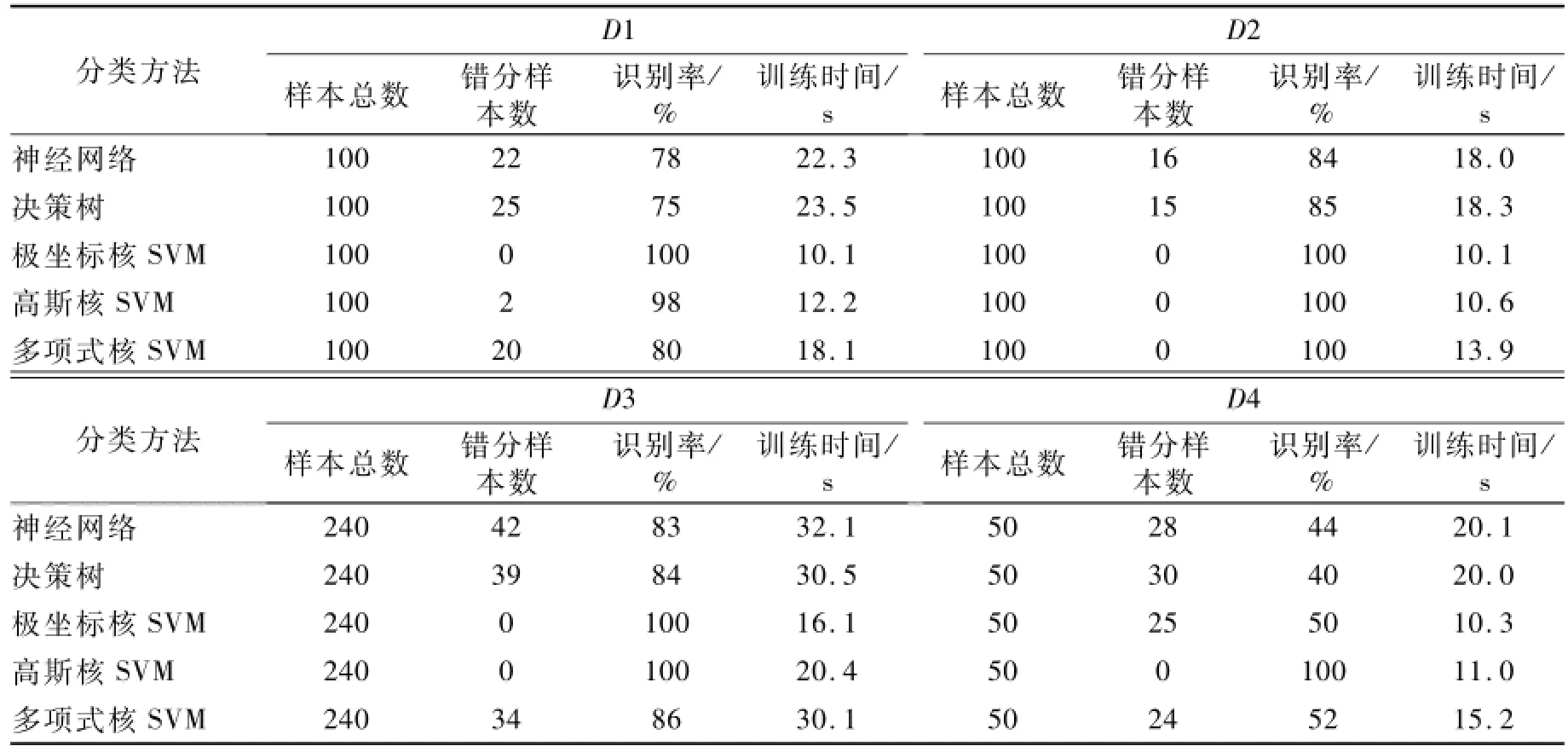
表1 采用不同方法的分类结果比较

2.2 实验结果分析

从实验结果可以看出：呈圆形分布的数据集D1、D2、D3，采用极坐标核进行分类实验的效果优于其他几种方法，分类效果最好。

由文献［4］可知：运用极坐标核进行分类实验，原始数据经过映射φ到达特征空间：

分析该函数可以计算出：只要数据集满足圆形分布，经过该映射φ在特征空间可以被一条直线有效地分割开。因此，呈圆形分布的数据集采用极坐标核进行分类实验，识别率可达到100%，分类效果好。

3 结束语

本文提出一种结合数据分布特征进行核选择的方法，实验结果证明了该方法的有效性和正确性。本文仅讨论了呈圆形分布的数据集如何有效地选择核函数，而数据集的分布是多样化、复杂化的，数据集呈其他形状分布时，SVM核函数的正确选取值还需进一步探讨和研究。

［1］ Vapnik V.The Nature of Statitiscal Learning Theory［M］.New York：Spring Verlag Press，1995.

［2］ Wang W J，Xu Z B，Lu W Z.Determination of the Spread Parameter in the Gaussian Kernel for Classification and Regression［J］.Neurocomputing，2003，55（3）：643－663.

［3］ 孙建涛，郭崇慧，陆玉昌，等.多项式核支持向量机文本分类器泛化性能分析［J］.计算机研究与发展，2004，41（8）：1321－1326.

［4］ 张莉，周伟达，焦李成.一类新的支撑矢量机核［J］.软件学报，2002，13（4）：713－718.

［5］ Wang X M，Chung F L，Wang S T.Theoretical Analysis for Solution of Support Vector Data Description［J］.Neural Networks，2011，24（4）：360－369.

［6］ Gao SH，Tsang IW H，Chia L T，et al.Local Features are not Lonely Laplacian Sparse Coding For Image Classification［J］.CVPR，2010，18（6）：126－138.

［7］ 周伟达，张莉，焦李成.一种改进的推广能力度量标准［J］.计算机学报，2003，26（5）：598－604.

［8］ Wu S，Amari S.Conformal Transformation of Kernel Functions：A Data-dependentWay to Im prove Support Vector Machine Classifiers［J］.Neural Processing Letters，2002，15：59－67.

［9］ Chapelle O，Vapnik V.Model Selection for Support Vector Machines［C］／／Smola A，Leen T，Mullereds K.Advances in Neural Information Processing Systems 12.Cambridge，MA：MIT Press，2001.

［10］ Choi Y S.Least Squares One-class Support Vector Machine［J］.Pattern Recognition Letters，2009，30（13）：1236－1240.

［11］ Cox T，Cox M.Multidimensional Scaling［M］.London：Chapman＆Hall，1994.

［12］ W idyanto M R，Nobuhara H，Kawamoto K，et al.Improving Recognition and Generalization Capability of Back-propagation NN［J］.Applied Soft Computing，2005，6（1）：72－84.

［13］ Brydon M，Gemino A.Classification Trees and Decision Analytic Feedforward Control：A Case Study from the Video Game Industry［J］.Data Ming and Know ledge Discovery，2008，17（2）：317－342.

TP301

A

1672－6871（2014）03－0055－03

国家自然科学基金项目（61273291）；山西省高等学校科技研究开发项目（20121131）；山西大学商务学院基金项目（2012014）

郭金玲（1982－），女，山西长治人，讲师，硕士，主要从事机器学习与数据挖掘方面的研究.

2013－09－01