战斗机后体流场数值模拟与减阻优化设计

徐 嘉，蔡晋生，刘秋洪

（西北工业大学 翼型叶栅空气动力学国防科技重点实验室，陕西 西安 710072）

0 引 言

减阻技术，一直是飞机设计研究中的热点问题。现代喷气战斗机的后体阻力大约占到全机阻力的38%～50%［1］，所以有必要对这类阻力进行研究。研究后体阻力之前，首先需要对飞机后体流场进行准确的预测。早期科研人员通过采用风洞实验的方法得到后体喷流流场信息［2－3］。随着计算机与数值方法的发展，科研人员采用数值方法研究飞机后体喷流与外流相互干扰问题［4－6］。

战斗机后体外形设计方法通常是将表面外形设计成流线型，避免后体流场对喷管的不利干扰，使得喷管表面得到很好的再压缩［1］。Catt等［7－8］对 F－16战斗机后体外形进行减阻设计，通过延长后体长度，改变后体外形曲线等方法降低后体阻力。这种设计的思路就是保证战斗机后体外形表面光滑流线，不发生流动分离，从而达到良好的减阻效果。由于方案设计取决于实际经验，因此具有一定的局限性。随着CFD理论的不断深入，科研人员开始探索新的减阻技术。Kentfield［9］提出了后体多台阶被动减阻方法，与原有的减阻思路不同，外形表面并不是设成光滑流线，而是用多个阶梯代替。当气流流过阶梯时，阶梯内产生环形涡，使得流向膨胀相对较小，表面压力得到很好的恢复，从而降低了后体阻力。对于超声速和高超声速流动，这种方法能够降低后体阻力，但是对于不同的飞行状态，需要设计相应的台阶数目和位置。除此之外，还有多种主动减阻措施，如喷流、微吹吸气、振动壁面等，这样飞机必须添加额外机构或系统才能实现，往往会增加自重。被动减阻措施，如鼓包修形［10］，凹陷修形［1］等，在亚声速飞行状态，不但不能减阻反而还会使阻力增大，只有在特定的飞行状态下的被动减阻措施才有明显减阻效果。

本文通过计算二维轴对称N－S方程、k－ω SST湍流模型和组分方程，对战斗机后体绕流与尾喷流进行数值模拟，研究不同喷流介质和喷压比对后体阻力的影响。为了降低后体阻力，提高战斗机的气动性能，采用梯度法［11－12］对后体外形进行减阻优化设计。与其他优化方法相比，梯度法简单、实用，但是计算效率不高。为了提高梯度法的优化效率，本文提出一种优化设计点加速算法。

1 后体流场数值模拟

1.1 流场计算方法

流动控制方程为二维轴对称Navier－Stokes方程，采用有限体积法对方程进行离散求解，方程中的对流项采用二阶精度的Roe－FDS格式［13］进行离散，粘性项采用中心差分格式，通过隐式LU－SGS［14］进行时间推进。湍流模型选用k－ω SST模型，以k－ω为基础的剪切应力输运（SST）模型计算湍流剪切应力的输运项，准确模拟在逆压梯度下边界层湍流剪切应力的影响［15］。

假设当前发动机内燃烧完全，流动过程中不考虑化学反应，燃气喷流可视为多组分的冻结流。混合物中每一种组分气体都满足气体状态方程，假设相同控制体内每种组分气体温度相同，对浓度相对较大的水蒸气、氧气和氮气进行数值模拟。不同气体质量组分方程采用以下形式：

其中Yi为第i种物质质量分数，Ji为物质i的扩散通量。

1.2 后体几何外型

本文采用的后体几何外型与文献［16］进行实验的几何外型相同，图1给出了几何外型尺寸示意图。坐标轴x，y分别沿对称轴及径向，原点位于尾喷管喉道o点处，箭头表示气流流动方向。机身直径d＝0.1524m，后体出口高度e＝0.03885m，内喷管喉道处高度t＝0.02935m，收缩段长度s＝0.1084m，扩张段长度f＝0.1506m。

1.3 计算网格和边界条件

根据图1所示后体几何外型，生成如图2所示的计算网格。后体外流场计算网格为H型结构网格，网格边界到物面距离为15倍后体直径，根据来流雷诺数Re∞确定物面边界层网格的尺寸为2×10－5左右。喷管内流场网格为H型结构，在喷管内流场与外流场剪切层区域分布较密网格。

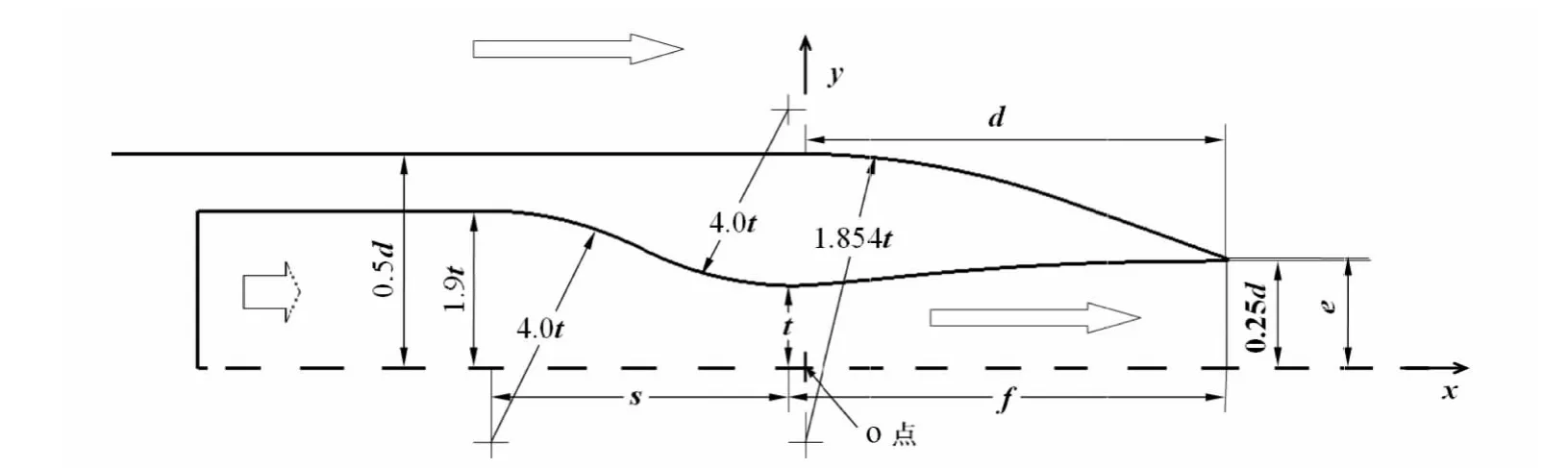
图1 计算模型示意图Fig.1 Computational model

物面采用绝热、无滑移边界条件，侧向与前缘远场边界取无反射边界条件，下游远场边界采用压力出口边界条件。在内流场的喷管进口处，指定喷流马赫数Mj与喷流温度Tj。当Mj＜1时，喷管进口静压值pj由计算域外推得到；当Mj＞1时，pj取指定值。

1.4 计算结果与分析

1.4.1 后体流场特性

为了验证计算方法与网格的可行性，采用文献［16］的实验来流条件，马赫数Ma∞为1.2，迎角α为0°，基于机身直径的雷诺数Re∞为14.06×106，喷管出口马赫数Mae为2.0，出口总温Ttotal为1013K，喷管压比pt，j／p∞（Nozzle Pressure Rates，简称 NPR）为8，喷流介质组分为57.7%水蒸气和42.3%氧气，水蒸气和氧气不再发生化学反应，喷流气体的比热比γ为1.265，气体常数R 为376.19J／kg·K，外场气体由77%氮气和23%氧气组成。

图3为后体表面压力分布与流线图，图4为后体流场马赫数云图。从图3中可以看到，本文的计算结果与文献的实验结果几乎吻合，由于外流在x／d为0.0的位置以后经历了一个膨胀加速的过程，气流加速使得表面压力降低，所以在0.0＜x／d＜0.56区间内后体压力值逐渐降低，在x／d为0.56左右的位置达到最低点之后迅速升高，这是由于跨声速气流在流过后体表面膨胀加速后在x／d为0.56左右的位置产生激波。由于后体表面激波导致边界层流动分离而产生分离涡，如图3的流线图所示。

图5为喷流马赫数分布云图，从图中可以看到，喷流与外流相互作用形成剪切层，喷口处的膨胀波在中心线处相互作用后延伸至喷流边界反射形成压缩波，多个压缩波叠加在一起形成一道截断膨胀波的拦截激波以及马赫盘。

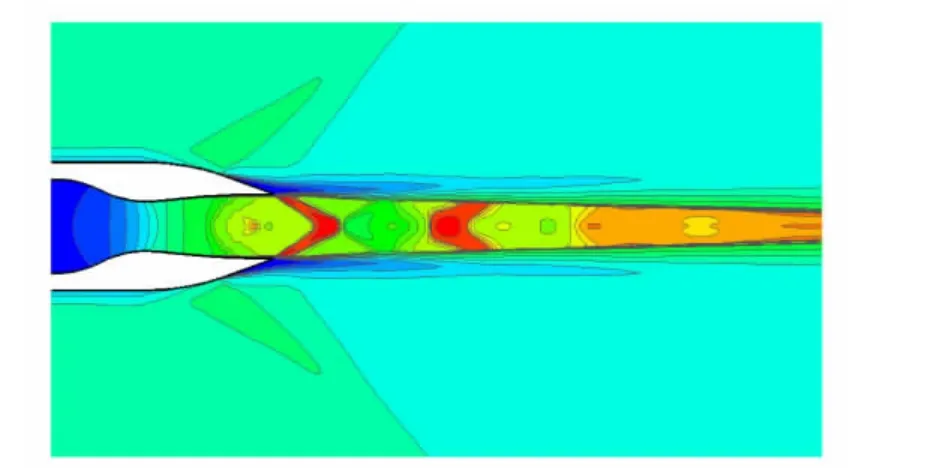
图5 喷流马赫数云图Fig.5 Contour of Mach number on jet

1.4.2 喷流介质对后体阻力的影响

喷流气体介质的比热比是影响喷流和外流相互作用的一个重要参数，多组分气体的比热比随着流场气体质量变化而变化，理想气体的比热比为常数，现在研究不同比热比的喷流气体对后体阻力的影响。来流边界条件与1.4.1节相同，两种喷流气体介质和出口参数如表1所示。

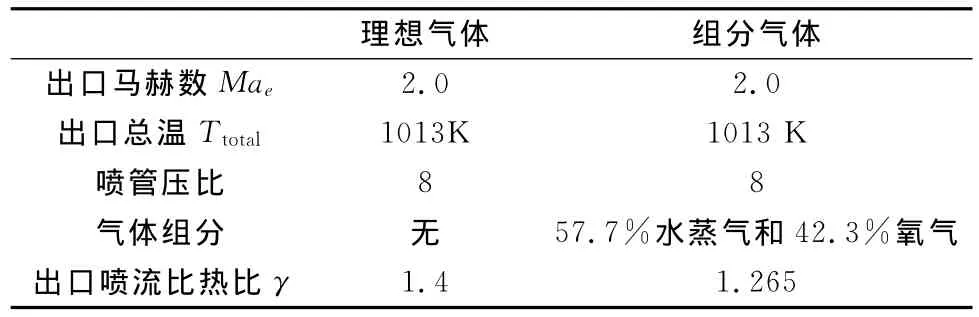
表1 喷流介质出口状态参数Table 1 The parameters for jet flow

图6为理想气体喷流介质实验与计算，以及组分气体喷流介质计算后体表面压力分布比较图。从图中可以看到，与组分气体喷流介质后体压力分布相比，理想气体喷流介质的后体表面压力分布的激波位置略靠后。采用理想气体作为喷流介质的后体外形阻力系数为0.199，组分气体喷流介质的后体阻力系数为0.184，理想气体喷流介质的阻力系数高于组分气体喷流介质的阻力系数7.5%。由于采用组分气体做喷流介质需要求解组分方程，造成数值计算中计算量的增加。在优化设计的过程中，在不影响计算精度的情况下，为了降低计算量在优化设计中可采用理想气体作为喷流介质。

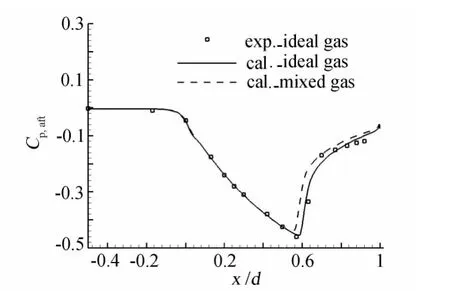
图6 后体压力分布比较Fig.6 Comparison of pressure distribution

1.4.3 喷管压比对后体阻力系数的影响

喷管压比对后体表面压力分布有较大的影响，通过模拟不同喷管压比的后体流场，研究喷管压比对后体阻力系数的影响。采用1.4.2节相同的流场条件，表2给出不同喷管压比下后体阻力系数的变化。可以看到，后体阻力系数随喷管压比的增大而减小。因为随着喷管压比的增大，喷流膨胀主要对后体尾部产生较大的压力分布，从而降低后体压差阻力。

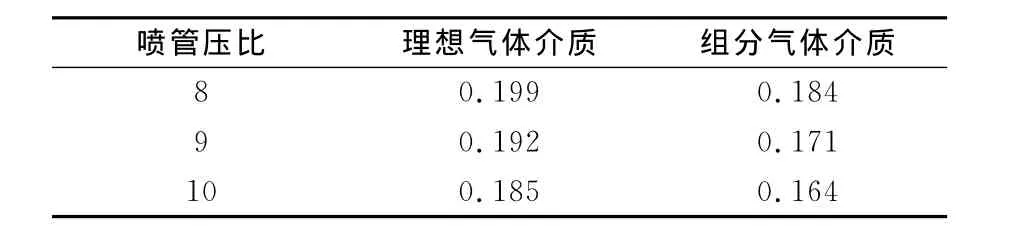
表2 不同喷管压比下的阻力系数Table 2 Drag coefficients with different pressure rates

2 后体减阻优化设计

2.1 优化设计方法

应用梯度法对后体外形进行减阻优化设计。在优化之前，需要构造设计变量与目标函数，如图7所示，从后体外形上选取n个设计控制点，第i设计控制点的坐标值为（xi，yi），设计控制点轴向坐标xi值取后体弦长的i个平均值，设计控制点径向坐标yi值为设计变量，采用三次样条插值函数来表示后体外形，确定后体起始点O处的一阶导数值和N点的自然边界插值，以保证后体外形与机身平直段的光滑过渡。

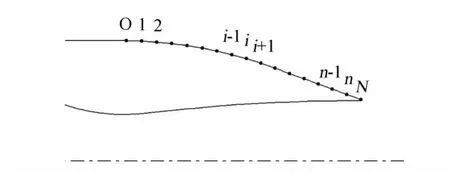
图7 后体外形及初始优化控制点分布示意图Fig.7 Design pointes and optimal model of afterbody

定义后体阻力系数为：

其中，U∞为来流速度，ρ∞为来流密度，Daft为后体阻力。以径向坐标y值为设计变量，最小阻力系数Cd，aft为设计目标，定义目标函数为：

梯度法优化后体外形的具体过程如下：

（1）给定初始点y0，初始搜索步长λ0和误差限0＜ε≤1迭代步数i＝1

（2）计算搜索方向si＝ －▽f（yi），代入到迭代公式yi＋1＝yi＋λi·si；

（3）根据径向坐标yi＋1值和轴向坐标x值得到后体外形优化曲线，应用CFD计算出后体阻力系数Cd，aft，即得到f（yi＋1）；

（4）若‖f（yi＋1）－f（yi）‖≤ε，则停止计算，yi＋1所确定的后体外形为最终优化外形；否则，求最优步长λi＋1，使得不等式f（yi＋λi＋1·di）＜f（yi）成立。

（5）令i＝i＋1，转（2）。

2.2 优化设计加速算法

梯度法产生每一优化步的搜索方向都要用到目标函数的梯度信息，求解流场的次数取决于设计控制点个数，当设计控制点个数比较多时，求解流场的次数会很多。选取少量的设计控制点虽然能够降低优化时间，但是不可能得到最优的设计外形。所以，本文提出一种梯度法优化设计的加速算法，即基于后体外形曲率值，逐步增加设计控制点数目并合理分布设计控制点的位置，从而提高优化设计的效率和精度。

对于给定的后体外形曲线，其曲率分布为k（x），在曲线上布置n个优化控制点（后体外形曲线的起始和终止位置相对固定，因此不作为设计控制点），可以得到设计控制点之间的区域数为m＝n＋1，定义区域曲率与长度积分的平均值为：

可以得到设计控制点的轴向坐标x1，…，xi，…，xn，使下式成立，

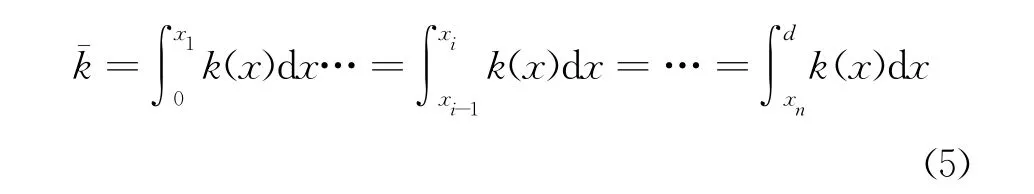
式（4）表示优化控制点之间区域曲率相对长度积分值相同，使得设计控制点在外形曲率值较大的区域分布比较密集，而曲率值较小的区域分布比较稀少，这样就可以采用较少的控制点来精确地描述较为复杂的外形曲线。

采用梯度法进行优化设计，先选取少量的设计控制点对初始外形进行优化设计，使目标函数基本达到最优。然后增加设计控制点个数，通过计算外形曲线的曲率对所有设计控制点重新进行分布，对后体外形进行重新描述，采用梯度法进行新一轮优化设计。重复上述逐步增加设计控制点过程，最终达到优化设计目标。如图8所示为基于曲率逐步增加设计控制点方法与梯度法相结合进行优化设计的流程示意图，其中Cd为新一轮优化得到后体阻力值，Cd＿t为目标值，一般取没有结合加速算法直接梯度法优化得到的后体阻力值。

图8 优化设计流程示意图Fig.8 The flow chart of the optimization

2.3 优化设计结果与分析

2.3.1 后体减阻优化结果

以1.4.1节算例中的计算外形为初始外形，采用相同的来流条件进行后体减阻优化设计。流场数值计算结果发现喷流介质气体组分对后体阻力影响较小，为了减少优化设计中流场数值计算的时间，不考虑喷流介质中气体组分的影响，以理想气体为喷流介质。喷管出口马赫数Mae为2.0，出口总温Ttotal为1013K，喷管压比NPR为8。取11个设计控制点进行后体外形减阻优化设计，设计点轴向坐标xi值取后体弦长的i个平均值，即在初始外形上均匀分布设计点。

图9对比优化前后的后体外形，实线是优化后的外形，虚线是优化前的初始外形，实线上的点为均匀分布的设计控制点。与初始外形相比，优化外形出现了一个类似“鼓包”形状，外形其他部分表面光滑平直。

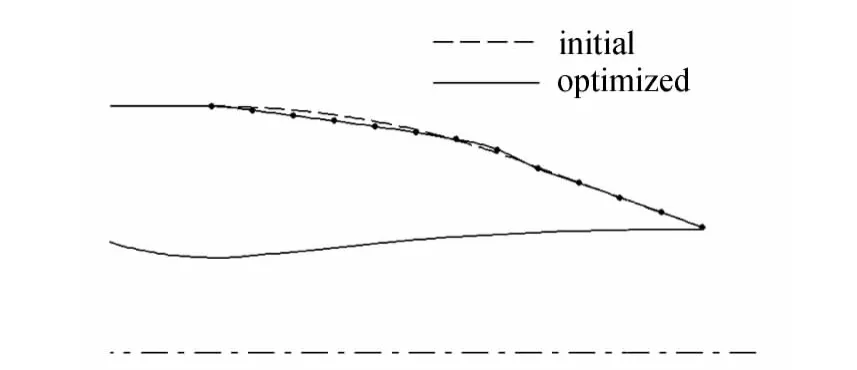
图9 初始与优化外形Fig.9 Initial and optimal shape

图10为优化前后外形表面压力分布比较，实线（optimized）是优化后的外形表面压力分布，虚线（initial）是初始外形表面压力分布。比起初始外形的压力分布，在0＜x／d＜0.5区间内优化外形的压力不降反升，压力最低点也要高于初始外形。优化前后的后体阻力系数的计算结果分别为0.199和0.178，优化后的外形使得后体阻力系数降低了10.6%。在初始外形与优化外形的前段，外流都进行了一个膨胀加速的过程，比起初始外形，优化外形表面表过渡的曲率变化小，后体表面压力得到恢复，从而降低了后体阻力。在激波位置附近，优化外形出现了一个类似“鼓包”形状，弱化了激波强度，减小了压力损失。

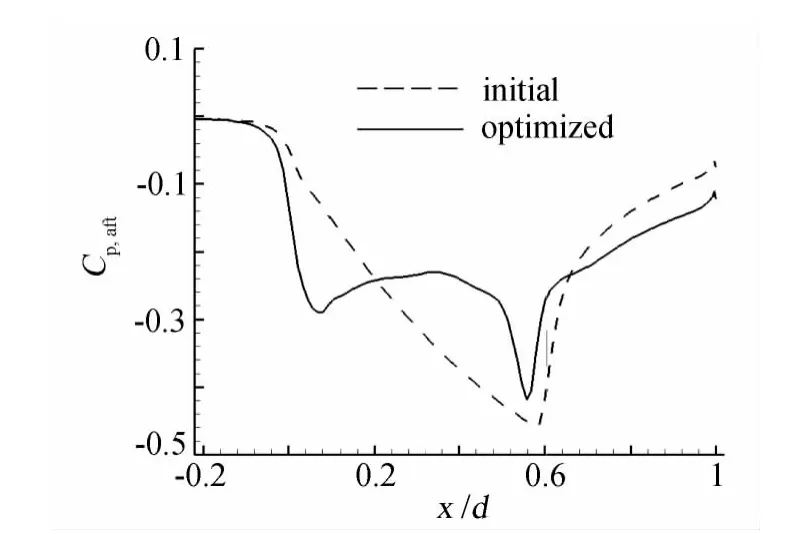
图10 优化前后的后体表面压力分布Fig.10 Pressure distribution

2.3.2 优化设计加速算法结果分析

采用本文提出的优化设计加速算法法与梯度法相结合进行后体减阻优化设计，可以提高优化设计的效率和精度。先在初始外形上均匀布置2个设计控制点，得到2点优化外形。然后增加3个优化控制点，采用基于外形曲率的设计控制点分布方法重新分布5个优化控制点位置，进一步得到5点优化外形。为了更好地描述后体外形局部形状，特别是曲率变化较大区域，在5个优化控制点优化外形的基础上再增加6个优化控制点，采用同样的方法重新分布11个优化控制点，通过梯度法进行优化计算得到最终优化外形。

图11至图13分别给出采用2、5与11个优化控制点进行优化设计得到的外形与初始外形的对比。图中实线是优化后外形，虚线是初始外形，实心点为设计点。从图13中可以看到采用11个优化控制点进行优化设计，设计控制点主要集中分布在激波区域的“鼓包”附近以及后体起始位置附近。采用2、5和11个设计控制点优化得到的后体阻力系数分别为0.184、0.178和0.175，与初始外形相比，最终得到的优化外形使得后体阻力系数降低了13.0%。与直接均匀分布11个优化控制点采用梯度法进行优化设计的方法相比，本文提出的逐步增加设计控制点个数并根据外形曲率合理分布设计控制点位置与梯度法相结合的优化设计加速算法能够得到更好的优化结果。

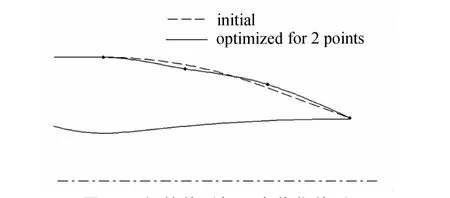
图11 初始外形与2点优化外形Fig.11 Initial and 2－point optimal shape

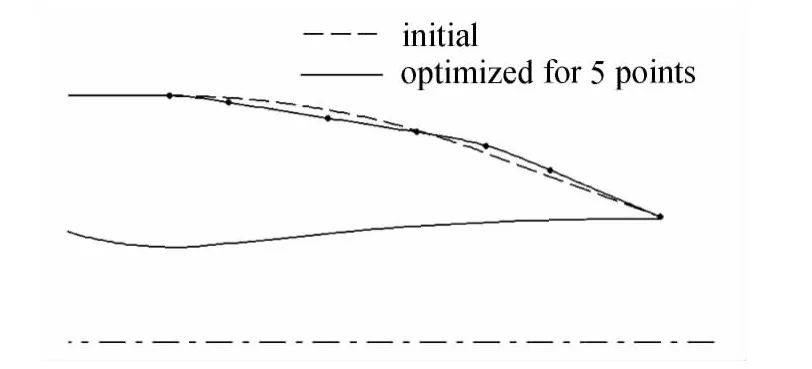
图12 初始外形与5点优化外形Fig.12 Initial and 5－point optimal shape

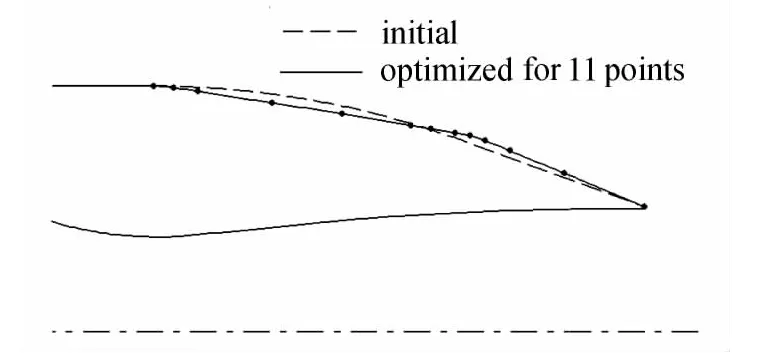
图13 初始外形与11点优化外形Fig.13 Initial and 11－point optimal shape

图14为优化过程中的收敛曲线图，实心点划线（11design）为直接11设计控制点梯度法迭代曲线，空心点划线为逐步增加设计控制点方法迭代曲线。直接11设计控制点梯度法优化迭代了26步，平均迭代1步需要3.07小时，完成11点优化外形最终花费79.8小时。逐步增加设计控制点方法共计优化迭代了32步，其中2设计控制点迭代18步，每步需要0.87小时，5设计控制点迭代7步，每步需要1.45小时，完成优化计算最终花费47.3小时。与直接11设计控制点梯度法优化方法相比，这种优化加速算法使得优化计算时间降低了40%左右。

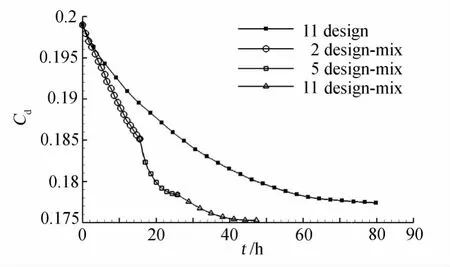
图14 收敛曲线Fig.14 Convergence curve

3 结 论

本文通过数值计算二维轴对称Navier－Stokes方程、k－ω SST湍流模型和气体组分方程，分析飞机后体流场特性，并进行后体减阻优化设计。通过本文的数值分析，可以得到以下的几点结论：

（1）由于后体表面激波导致边界层流动分离而产生分离涡。喷流与外流相互作用形成剪切层，喷口处形成一系列膨胀波和压缩波以及马赫盘。在跨声速来流下，理想气体喷流介质的后体阻力系数略高于组分气体喷流介质的后体阻力系数，而阻力系数随着喷管压比的增大而减小。

（2）通过优化设计得到的后体外形曲率变化缓慢，使得表面压力得到恢复，后体外形在激波位置附近出现“鼓包”形状，弱化了激波强度，与原始外形相比后体阻力值降低13%。

（3）优化设计加速算法逐步增加设计控制点个数，并根据外形曲率合理分布设计控制点的位置，更好地描述外形曲线。优化结果表明，该算法不仅能够有效的降低优化设计时间，而且还能够提高优化设计精度。

［1］方宝瑞.飞机气动布局设计［M］.北京：航空工业出版社，1997.

［2］CHAMBERLAIN D.Measurement of drag from interaction of jet exhaust and surrounding airframe［R］.AIAA Paper 68－395，1968.

［3］PRESZ W M，PITKIN E T.Flow separation over axisymmetric afterbody models［R］.AIAA Paper 74－17，1974.

［4］DEIWERT G S，AANDREWS A E，NAKAHASHI K.Theroretical analysis of aircraft afterbody flow［J］.J.Spacecraft ＆ Rockets，24（6）：496－503.

［5］蔡晋生，刘秋洪.超声速流场中侧向射流的数值研究［J］.空气动力学学报，2010，28（5）：553－558.

［6］张正科.用N－S方程有限体积法计算弹体绕流／底喷流［J］.空气动力学学报，2003，21（3）：288－294.

［7］CATT J A，WELTERLE T J.Decreasing F－16nozzle drag using computation fluid dynamics R .AIAA Paper 93－2572，1993.

［8］WELTERLEN T J，CATT J A C.Evaluating F－16nozzle drag using computational fluid dynamics［R］.AIAA Paper，94－0022，1994.

［9］KENTFIELD J A C.Drag reduction of controlled separated flows［R］.AIAA Paper，85－1800，1985.

［10］QIN N，WONG W S，LE Moigne A.Three－dimensional contour bumps for transonic wing dody drag reduction［A］.Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering［C］.2008.

［11］YUAN YA－XIANG.A new stepsize for the steepest descent method［J］.Journal of Computational Mathe－matics 2006242149－156.

［12］JONATHAN BARZILAI，JONATHAN M Borwein.Two－point step size gradient methods［J］.IMA Journal of Numerical Analysis，1988，8：141148.

［13］阎超.计算流体力学方法及应用［M］.北京：北京航空航天大学出版社，2006.

［14］VOS J B，LEYLAND P，KEMEMADE V V，et al.NSMB handbook version 5.0［R］.2003：36－38.

［15］MENTER F R.Zonal two－equation k－ω turbulence model for aerodynamic flows［R］.AIAA Paper 93－2906，1993.

［16］WILLIAM B Comptom Ⅲ.Effects of jet exhaust gas properties on exhaust simulation and afterbody drag［R］.NASA TR R－444，1975.