一类多参数平面微分系统的全局结构分析
刘艺艺,窦霁虹,赵红妮
(西北大学数学系,陕西 西安710127)
0 引言
平面多项式微分系统的定性理论在微分方程定性理论中占有重要地位,对它的研究大多集中在一个具体的系统。对于参数系统的研究具有重要的意义,当参数取定为某一值时,系统就成为一个新的系统,这样只需对一类参数系统进行研究,就可以得到一系列系统的随参数变化的性质。系统参数研究的方法一般是将其余参数看成常量,将要研究的参数看成唯一变量,对其进行研究[1,2];或者构造高阶方程,通过对高阶微分方程的研究确定原始系统的性质[3];还有利用不等式分析方法,通过放大或缩小不等式来寻找满足结果的若干条件[4];或是选取适当的条件,反过来求解参数应该满足的范围[5~11]。基于以上参数系统的研究方法,本文主要对系统

在a>0时进行定性分析,得到系统极限环的不存在性、存在唯一性的一些充分条件,并分析出系统参数变动对系统性态是如何影响的。
1 系统有限远奇点分析
求解方程组


当δ≥2时,O(0,0)为不稳定的结点;当0<δ<2时,O(0,0)为不稳定的焦点;当-2<δ<0时,O(0,0)为稳定的焦点;当δ≤-2时,O(0,0)为稳定的结点。
当δ=0时,O(0,0)为(1)对于线性系统的中心,应用形式级数法,得到:
(ⅰ)当l>0时,O(0,0)为稳定的焦点。
(ⅱ)当l<0时,O(0,0)为不稳定的焦点。
(ⅲ)当l=0时,系统(1)化为


(4)当n<0时,
2 系统无穷远奇点分析
2.1 对系统(1)作Poincare第一变换



系统(4)在B(u,0)对应的线性部分矩阵为


(1)当n>0,l≥0时;

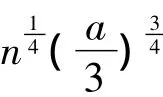
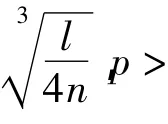


(2)当n>0,l<0时:





(3)当n<0时可类似的进行讨论。
2.2 对系统(1)作Poincare第二变换
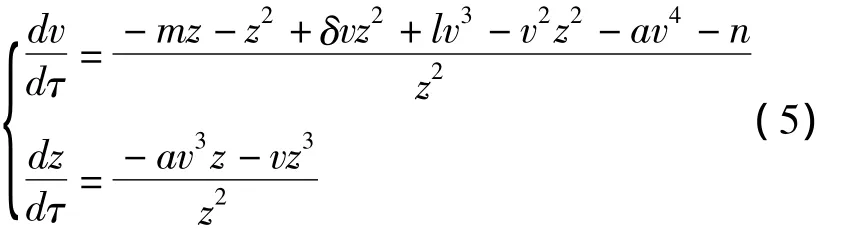

当n≠0时,D(0,0)不是系统(6)奇点;当n =0时,D(0,0)是系统的高阶奇点。
3 系统参数变动对系统性态的影响
综上所述,系统(1)的有限远奇点和无穷远奇点的性态如表1所示。
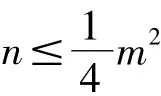
当n<0时可类似的进行讨论。

表1 系统(1)有限远奇点的性态

表2 系统(1)的无穷远奇点当n>0时的性态
4 系统极限环的分析
定理1:当lδ≥0且l2+δ2≠0时,系统(1)在全平面内不存在闭轨线。
定理2:当l=δ=0时,系统(1)存在一族围绕O(0,0)的闭轨线。
证明:由前面的讨论知,当l=δ=0时O(0,0)为系统中心,所以在O(0,0)邻域内充满闭轨线。
下面仅就lδ<0的情况讨论。
先给出引理1[13]。
引理1:考虑微分方程组
2.1.3.1 顺产不同时期BMI、新生儿体质量与盆底肌力治疗前后的相关性 顺产者盆底肌力减退治疗前后变化只与产后BMI存在正相关(P<0.05),见表6。
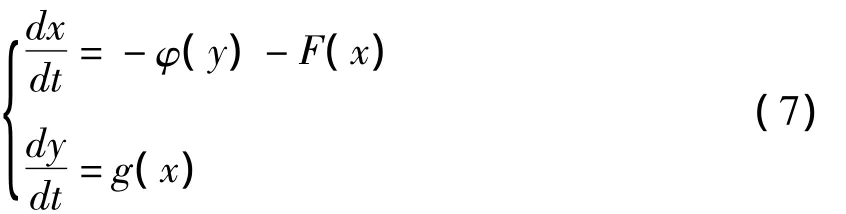
(1)当x≠0时,xg(x)>0;当y≠0时,yφ(x)>0;
(2)f(x),g(x),φ(y)连续可微;φ(y)单调递增;f(0)<0(f(0)>0);
(3)存在常数α,β,使f1(x)=f(x)+g(x)[α +βF(x)]有简单零点x1<0与x2>0,而且在区间(x1,x2)上f1(x)≤0(f1(x)≥0);
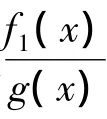
(5)所有闭轨线包围x轴上的区间[x1,x2],则系统(7)最多有一个极限环;如果它存在,则是稳定的(不稳定的)。
(1)当x≠0时,xg(x)=x2(ax2+1)>0;当y≠0时,yφ(x)=y2(ny2+my+1)>0;
(2)f(x)=F'(x)=-δ-3lx2连续可微,g (x),φ(y)连续可微;φ'(y)=3ny2+2my+1>0,φ(y)单调递增;f(0)=-δ<0;
(3)存在常数α=0,β=1,使f1(x)=-δ-3lx2+(x+ax3)(-δx-lx3),f1(1)>0,f1(-1)>0,f1(0)<0,则由函数连续性和介值定理,存在简单零点x1<0与x2>0,而且在区间(x1,x2)上f1(x)≤0;

(5)闭轨线若存在必包含O(0,0),所以所有闭轨线都包围x轴上的区间[x1,x2];则系统(1)最多有一个极限环;如果它存在,则稳定。
同理得到定理4。
5 结束语
本文主要对一类三次系统进行定性分析,并总结出参数变化对系统性态的影响,得到有关定理。对系统参数的讨论方法还可以应用于其它系统。
[1] 韩宝亮,王巍然,关 信.一类动力系统的参数变化的研究[J].东北电力学院学报,2001,21(3):38-41.
[2] 秦朝红,陈予恕.多频激励下Duffing-vanderPol系统的两参数分岔分析[J].应用数学和力学,2010,31 (8):971-978.
[3] 文传源.非线性、变参数系统的求解、分析与综合方法[J].系统仿真学报,2001,13(1):67-72.
[4] 崔宝同,邓飞其,刘永清.时滞分布参数系统的研究进展[J].应用数学,2003,16(1):8-16.
[5] 姜玉春,吴红燕.PID控制器参数的整定[J].莱钢科技,2006,(2):54-55.
[6] James A.Hansen.On stochastic parameter estimation using data assimilation[J].Physica D:Nonlinear Phenomena,2006,230(1):88-98.
[7] 袁燕飞,葛照强.一阶广义分布参数系统的指数稳定性[J].系统科学与数学,2010,30(3):315-322.
[8] Kairong Lin.An evaluation of impacts of DEM resolution and parameter correlation on TOPMODEL modeling uncertainty[J].Journal of Hydrology,2010,394 (3):370-383.
[9] 林 英.多时滞分布参数系统的滑模控制与稳定性[D].青岛:中国海洋大学,2011.
[10]魏 萍,丁 卯,等.一类抛物型分布参数系统的边界控制[J].控制工程,2013,20(5):837-840.
[11] Jing Wang.Parameter sensitivity analysis of crop growth models based on the extended Fourier Amplitude Sensitivity Test method[J].Environmental Modelling and Software,2013,48:171-182.
[12]陈文斌,高 芳,鲁世平.一类三次系统的奇点分析及极限环的存在性[J].安徽师范大学学报(自然科学版),2013,36(1):12-17.
[13]张芷芬,等.微分方程定性理论[M].北京:科学出版社,1985.
[14]马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.

