积分第一中值定理的推广
陈玉
(江西师范大学数学与信息科学学院,江西 南昌330022)
国内外的数学分析及微积分教材中,常见的积分第一中值定理是被积函数乘积因子g(x)在[a,b]上连续且不变号的积分第一中值定理的形式,即:
积分第一中值定理[1]:若f与g都在[a,b]上连续,且g(x)在[a,b]上不变号,则至少存在一点ξ∈[a,b],使得
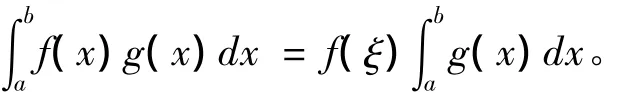
其中,要进一步证明中值点ξ可在开区间(a,b)内取到还另需繁复的证明。
本文将g(x)的条件减弱,用简便的方法直接得到中值点ξ可在开区间(a,b)内取到的结论,分别得到了闭区间与有限开区间上推广的积分第一中值定理。
1 闭区间上推广的积分第一中值定理
引理1[2]:设f(x)在[a,b]上连续,g(x)在[a,b]上有界且有原函数,则f(x)g(x)在[a,b]上有原函数。


证明:设F(x)为f(x)在[a,b]上的一个原函数,则由引理2可得
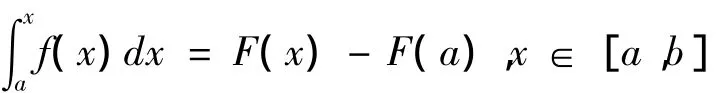
从而

定理1:设f(x)在[a,b]上连续,g(x)在[a,b]上可积且有原函数,g(x)≠0(a<x<b),则存在ξ∈(a,b),使得
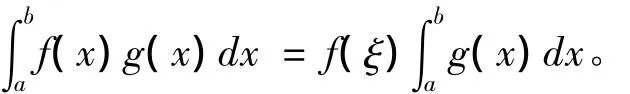

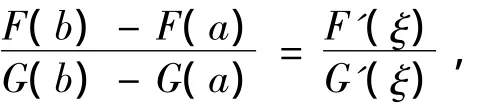
即
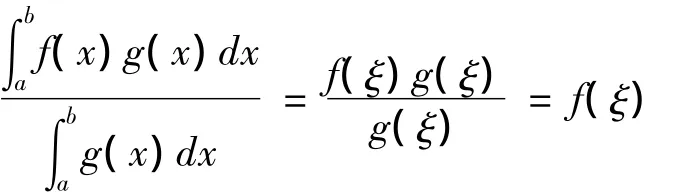
也即
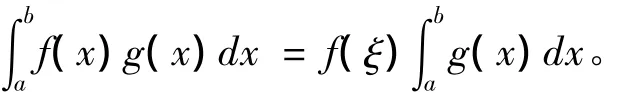
注1:由于可积但不连续的函数也可能有原函数[2],因此定理1的条件比积分第一中值定理更弱,并且用简便的证明方法直接得到中值点可在开区间内取到,从而推广了积分第一中值定理。
注2:定理1也是文献[4]推论4的推广。
文献[4]推论4:设f(x)、g(x)在[a,b]上连续,∀x∈[a,b],g(x)≠0,则存在ξ∈(a,b),使得
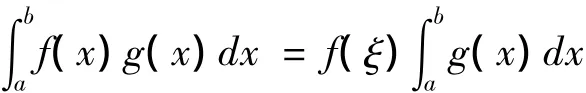
易见,文献[4]推论4可直接由定理1得到,成为定理1的一个推论,并且还可将条件“∀x∈[a,b],g(x)≠0”放宽为“g(x)≠0(a<x<b)”。
注3:定理1也可由文献[5]定理2(柯西型积分中值定理)直接得到一个更简洁的证明(见以下证2)。
引理4[5](柯西型积分中值定理):设f(x),g(x)在[a,b]上可积,且在[a,b]上有原函数,g(x)≠0(a<x<b),那么存在ξ∈(a,b),使得
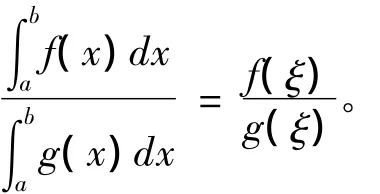
证2:g(x)在[a,b]上可积,从而g(x)在[a,b]上有界。由引理1得,f(x)g(x)在[a,b]上有原函数。又f(x)g(x)在[a,b]可积,f(x)在[a,b]上可积,且在[a,b]上有原函数,由引理4即得存在ξ∈(a,b),使得

也即
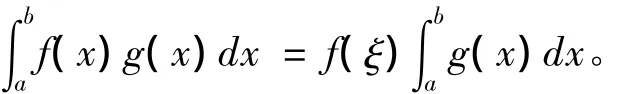
2 有限开区间上推广的积分第一中值定理
引理5[1]:设f(x)、g(x)均为定义在[a,b]上的有界函数,若仅在[a,b]中有限个点处f(x)≠g(x),则当f(x)在[a,b]上可积时,g(x)在[a,b]上也可积,且
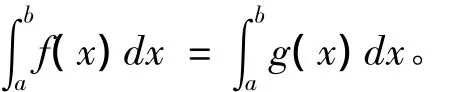
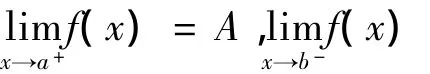
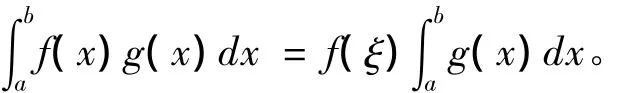
由F(x)在[a,b]上连续知F(x)在[a,b]上有界,则存在M>0,对所有x∈(a,b),有|F(x)|≤M,即|f(x)|≤M,(x∈(a,b)),则
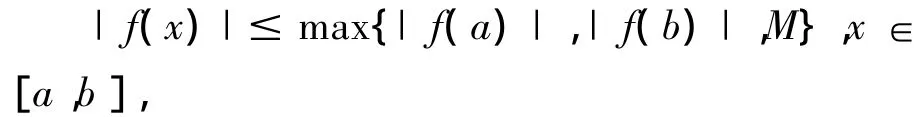
即f(x)在[a,b]上有界。由g(x)在[a,b]上可积,得g(x)在[a,b]上有界,从而f(x)g(x)在[a,b]上有界。又因为F(x)g(x)在[a,b]上有界,且仅在x=a,x=b处F(x)g(x)≠f(x)g(x)。
由引理5得,f(x)g(x)在[a,b]上可积,且

又因为F(ξ)=f(ξ),从而
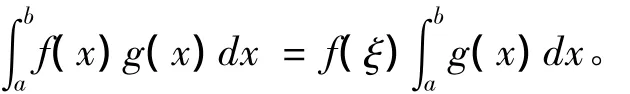
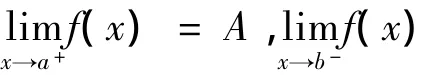
注4:定理2是定理1的推广,特别地,当A= f(a),B=f(b)时,定理2即为定理1。同理,推论是文献[4]推论4的推广,当A=f(a),B=f(b)时,推论即为文献[4]推论4。
[1] 华东师范大学数学系.数学分析(第三版)[M].北京:高等教育出版社,2001:212.
[2] 周民强.数学分析(第二册)[M].上海:上海科学技术出版社,2003:24-39,328.
[3] 周民强.数学分析(第一册)[M].上海:上海科学技术出版社,2002.
[4] 伍建华,孙霞林,熊德之.一类积分型中值定理的渐近性讨论[J].西南师范大学学报(自然科学版),2012,37(8):24-27.
[5] 陈 玉.基于微分中值定理的积分中值定理[J].高等数学研究,2013,16(6):42-45.

