混合动力电动汽车转矩管理控制策略设计

庄怀天

(合肥工业大学交通运输工程学院，安徽合肥 230009)

0 引言

随着科学技术的发展，传统内燃机汽车、纯电动汽车、混合动力汽车和燃料电池汽车近年来发展迅速。然而，由于发动机及其相关技术的限制，内燃机汽车的能耗和排放很难有突破性的改善。纯电动汽车虽然能够实现零污染排放，但是受电池能量密度、寿命、价格等问题的制约，难以推广应用［1］。燃料电池汽车的可靠性和能量转换效率问题依然没有彻底解决。混合动力汽车的出现在一定程度上缓解了这种难题。

混合动力的关键技术是如何制定更好的控制策略，无论串联式还是并联式都是为了保证发动机在最佳效率区和最低排放区工作。恒温器模式、发动机跟踪器控制模式及基于规则型策略是串联式的代表。并联式的控制策略主要有:静态逻辑门限值策略、瞬时优化控制策略、全局优化控制策略和模糊逻辑控制策略。后三种控制策略同样适用于混联式，另外发动机恒定工作点策略和最优工作曲线策略是混联式特有的两种策略［2-4］。

现有控制策略或多或少存在一些问题而不能满足要求，模糊控制由于其独特的性质在一定程度上缓解了这种矛盾。

1 设计模糊控制策略

传统控制策略依赖的是被控系统的数学模型，而模糊控制则是依赖于被控系统的物理特性。必须将这些物理特性抽象总结成为一系列概念和规则，然后才能推理得到有意义的结果。为了实现此过程，必须构造模糊控制器。

该模糊控制器由两个输入变量，一个输出变量构成。行驶过程中发动机输出转矩大小取决于总需求转矩，不仅要求电池荷电状态值SOC能稳定在适当的范围内，还要保证行驶过程中获得良好的动力性和经济性。因此将离合器模块输出的总需求转矩Treq、电池模块得到的电池SOC作为模糊控制的输入量，发动机输出转矩Tice为输出变量［5-7］。所构建的模糊控制系统框图如图1所示。

图1 模糊控制系统框图

1.1 模糊控制量化

在输入之前需要对实际输入变量进行尺度变换，以达到规定的论域范围，然后再做量化处理，其结果作为模糊推理系统的输入值。同样，系统的输出值也需要进行相应的处理。比如，若SOC实际的输入量Q*在［，］范围内变化，而要求的论域是［Qmin，Qmax］，这时就要采用线性变换进行处理，如式(1)。这里我们将SOC的实际变化范围定义在［0，1］内，所对应的论域为［0，11］。

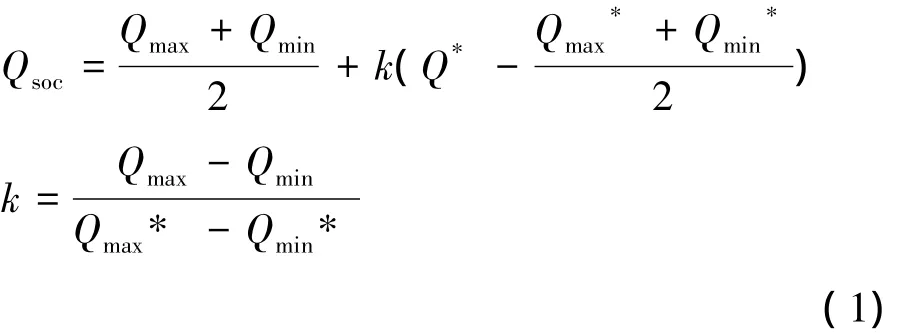
式中:Qsoc是经过尺度变换之后的值，k是比例因子。

根据式(1)把变换结果作为模糊推理系统的输入。

1.2 模糊化

在模糊控制应用中，被观测量通常是在一定精度范围内的数值量，由于模糊控制中操作是基于模糊集合理论的，因此，首先必须进行模糊化［8］。模糊化的核心思想是定义一个从数值域到语言域的模糊的语言映射关系，以便实现模糊推理。人们通常把输入变量分为离散的若干等级以便操作，定义的级数取决于精确度。对于一个模糊输入变量e，其模糊子集可以采用NB，NS，ZO，PS，PB表示输入或输出变量由负大、负小、零、正小，正大的变化过程，输入、输出变量均采用1～17这17个数来表示由最小到最大的一个连续变化的过程，其中1表示最小的模糊子集，9表示输入、输出变量位于中间部分的模糊子集，17表示最大的模糊子集。模糊子集的大小表示了该值的高低。

1.3 隶属函数

隶属函数是一条曲线，它定义了论域上的点与0和1之间的隶属度，隶属度是表示一个数值属于某一区间的程度。隶属函数对于模糊推理系统的性能有着很大的影响，若想控制较灵敏，必须选择瘦窄的隶属度函数，相反的，控制就会较平稳和粗略。隶属函数的确定主要有模糊统计法、三分法、增量法和分析推理法。

为简化设计过程采用分析推理的方法，选择三角函数和梯形函数作为隶属函数。鉴于总需求转矩Treq、电池SOC和发动机的需求输出转矩都是由初始值零开始变化的，所以输入、输出变量的隶属函数均采用两边梯形隶属函数，中间为三角隶属函数的设计方法［9］。

1.4 模糊推理系统规则的制定

模糊规则表示为“if…then…”条件语句。在应用中，通常将采用的模糊规则用模糊控制规则表的行驶表示出来。可以从相关专家或者大量实验数据中得到模糊规则。但是这些规则都是相似的，所以还有解决他们的协调问题。既要保证模糊规则的完备性，又要保证模糊规则的相容性问题。

根据已有的工程经验，设计模糊推理系统的控制规则，输入的总需求转矩和SOC各有17个模糊子集，因此形成17×17=289条模糊规则，再由混合动力汽车行驶过程总满足的动力性和经济性得到表1的控制规则。

表1 模糊推理系统控制规则

1.5 反模糊化

当输出量构成一个模糊输出集μB(y)时，为了产生能够表达模糊系统输出的单值必须压缩其分布，即反模糊化。实现反模糊化常用的方法有最大值平均和重力中心算法。相比较而言，重力中心反模糊化算法便于产生一个更加平滑的输出曲面。故本次设计就是采用重力中心反模糊化的方法。根据式(2)得到发动机输出转矩为:

式中:T0为发动机需求输出转矩的精确值;T为模糊值;a、b分别表示T所在论域范围的上下限值。

2 控制策略的嵌入和仿真

将制定好的控制策略嵌入到整车模型中进行仿真，以观察所制定的模糊逻辑推理系统是否满足要求。

2.1 模糊控制转矩控制策略的仿真

在ADVISOR已经建立的仿真模型的基础上，将其原先的电辅助控制策略替换成模糊控制策略进行仿真比较。控制模块的仿真模型主要包括输入量化模块、模糊推理模块和输出量化模块。

由上文可知，首先要将总需求转矩量化到［0，11］的论域区间，并一分为二。如果总需求转矩≤T，需求转矩量化到［0，6］的论域内;否则量化到［6，11］的论域内。Treq为总需求转矩，Ttarget为发动机目标转矩，它们与特定转速下发动机的效率和排放、温度、电机最大输出转矩有关，我们可以通过调整权重来调整其对目标转矩的影响程度。当然，在驾驶条件变化时权重系数随着仿真的进行而不断变化。模糊逻辑仿真模型如图2所示。

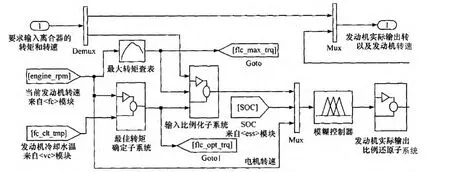
图2 模糊逻辑仿真模型

2.2 模糊逻辑控制系统嵌入Advisor

为验证所提出的模糊控制能量管理策略的有效性，需要将建立的模糊控制能量管理策略嵌入Advisor仿真软件进行仿真。由于笔者采用能量管理模糊控制策略，因此首先需将上述设计的能量管理模糊控制模块嵌入到Advisor软件的顶层控制模块，以便Advisor软件能够识别这个控制模块。然后把整车模型也嵌入Advisor中。完成管理策略嵌入和整车模型嵌入之后，即可对本文提出的能量管理模糊控制策略进行仿真验证。

2.3 仿真比较

如图3为电辅助控制策略仿真结果图。

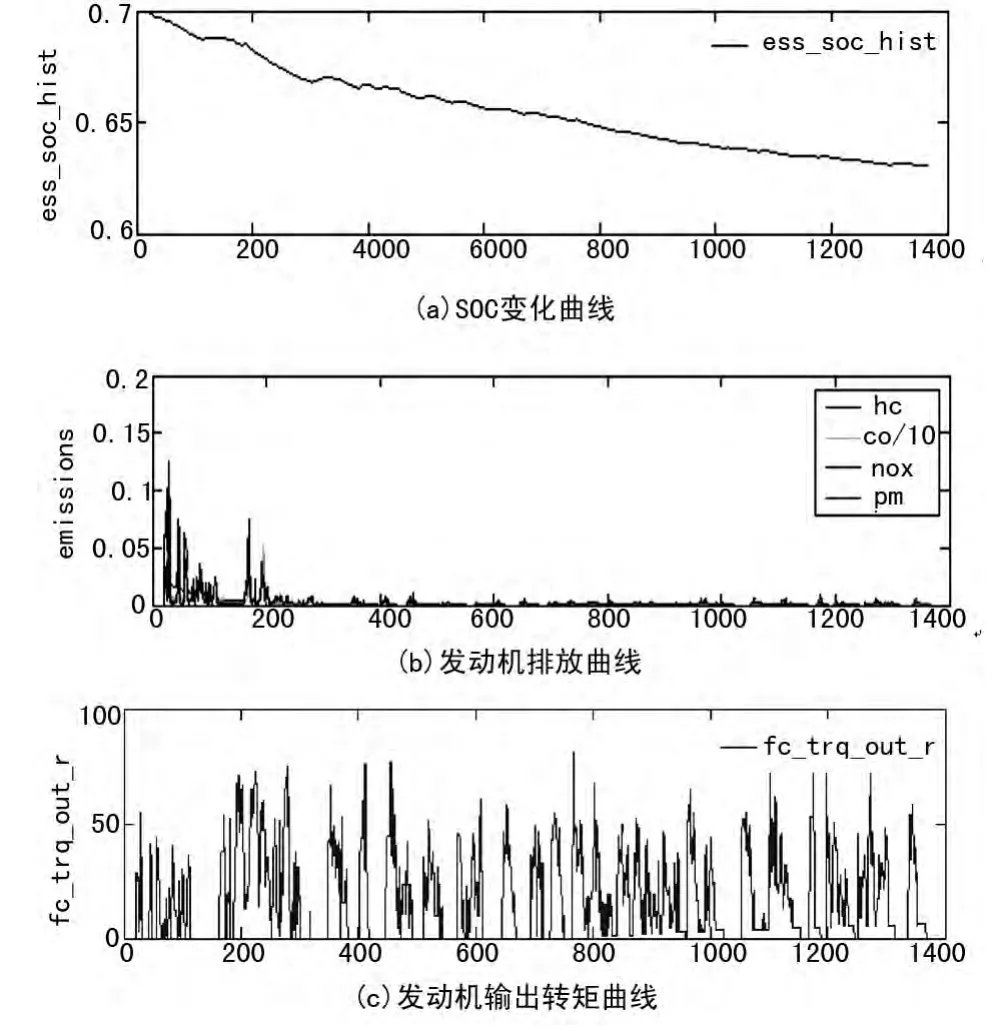
图3 电辅助控制策略仿真结果

在完成以上步骤之后，就可以进行对原有的电机辅助控制策略和模糊逻辑控制策略的比较分析，选择仿真的路况为CYC-UDDS，仿真时间1 369 s，仿真距离 7.45 miles，电池 SOC 初始值设定为 0.7。该道路循环下，停车17次，怠速259 s，需求的最大速度为56.7 km/h，最小速度为 19.58 km/h。仿真得电辅助策略如图3。将嵌入的模糊推理控制规则模型进行仿真，得到仿真结果如图4所示。在相同的仿真条件下，采用原有的电辅助控制策略的仿真结果如图3。

图4 模糊推理控制规则仿真结果

由图3(a)可知电池SOC的变化缓慢;由图3(b)可知，汽车起步时HC污染物的排放超过0.1，明显高于单模糊控制策略;由3(c)图可知，发动机提供主要动能，电机提供辅助动能。而采用模糊控制策略之后由图4可知，电池放电深度增加，更有助于整车燃油经济性的提高，并且发动机中的HC、CO、NOx的排放量明显降低。在电池SOC值较大的时候，在满足动力性的前提下发动机输出转矩较小，此时主要是由电池提供动力，当电池电量下降到一定水平时，发动机开始工作，此时发动机不仅提供行驶的动力，并且为电池充电。

由表2比较可看出采用模糊控制策略能够使得发动机的燃油经济性以及排放性能均有所提高，并且系统的总效率也由原来的0.103提高到现在的0.128。

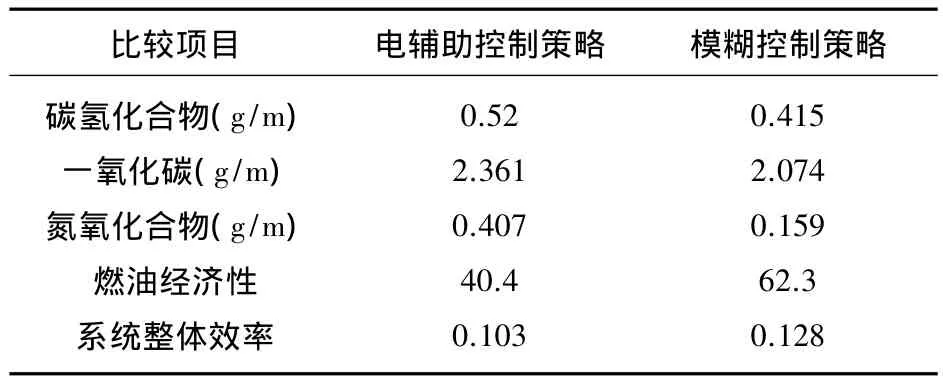
表2 两种控制策略的仿真结果比较

从电池充放电效率图5中可看出:电池充放电的效率保持在较高的水平，循环中始终保持在0.8以上。

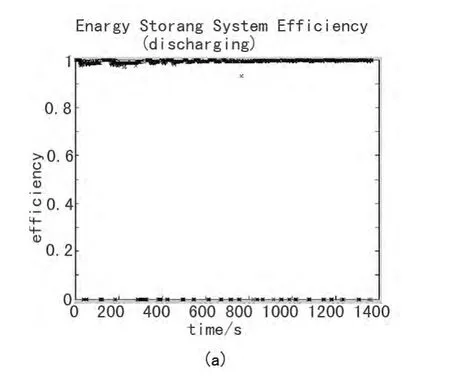
通过比较可知，嵌入模糊逻辑转矩控制策略的混合动力汽车，在保证动力性的前提下可有效的提高燃油经济性，可使电池的电量在一定范围内充分利用，当电池电量下降到一定程度时，发动机不仅提供汽车的行驶动力而且为电池提供能量，使电池电量不至于降到较低水平，从而延长电池的使用寿命。

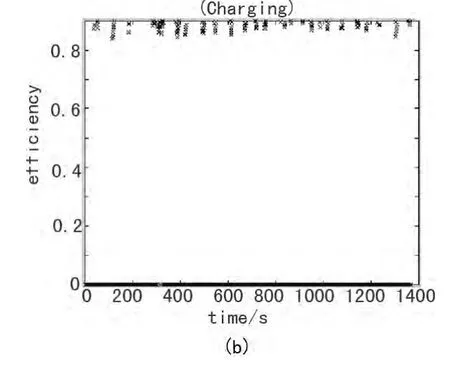
图5 电池充放电效率图

3 结语

详细介绍了模糊控制的基本原理、制定过程，指出首先要将输入输出量进行模糊化，然后根据工程经验，构建一个以总需求转矩和电池SOC值为输入，发动机输出转矩为输出的模糊控制器，并制定了相应的控制规则。在动力性和燃油经济性的基础上，将模糊子集尽可能的细化。同时对该控制策略进行仿真，通过对比得出模糊逻辑控制策略能够在保证动力性的前提下更好的改善燃油经济性。并且模糊规则的增多对这种效果更加显著。

如今各种控制策略层出不穷，但都存在一些问题。笔者提出细分模糊子集的缺点是不能做到无线划分，所以不能彻底解决问题。未来控制策略应该向两种或多种控制策略共同作用的方向发展。

［1］ 孙远涛，张洪田.混合动力汽车研究状况及发展趋势［J］.黑龙江工程学院学报(自然科学版)，2011(2):13-16.