基于Pro/E和ABAQUS的直齿轮强度分析
宋立伟,李风风,郑天虎
(中国一重重型技术装备基础科学研究院,辽宁大连 116600)
0 引言
海洋平台传动系统中,齿轮传动是核心部分,要求齿轮传动系统具有体积小、强度大等优点[1],能够准确的校核齿轮强度具有非常重要的意义。齿轮强度校核标准一般采用AGMA标准,得到的结果相对保守。ABAQUS是一款可做静力学和动力学分析的软件,模拟齿轮的动态啮合,得出齿轮接触对最大接触应力,并与传统理论计算结果相比较,为齿轮的进一步优化设计提供条件。
1 齿轮接触强度的理论分析
一对相啮合的直齿轮,已知输入功率P=26.7 kW,传递扭矩T=818 N·m,小齿轮转速n1=311 r/min,工作寿命 t=1 000 h,传动比 u=3.2。齿轮的基本几何参数见表1所列。

表1 齿轮几何参数
2 AGMA齿轮强度承载能力的计算
2.1 AGMA接触强度计算理论[2]
接触强度计算公式以两曲面接触的赫兹接触应力公式为基础,并考虑相邻齿间载荷分配的影响加以修正,即:
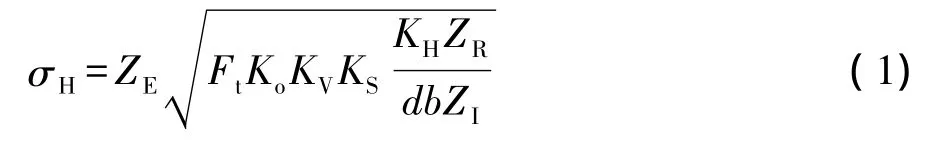
式中:材料的弹性系数ZE=189.812;切向载荷Ft=13 088 N;过载系数Ko=1.25;动载系数KV=1.05;尺寸系数KS=1;载荷分布系数KH=1.163;接触强度齿面状况系数ZR=1;相啮齿轮最小净齿宽b=50 mm;接触强度几何系数ZI=0.11;小轮节圆直径d=125 mm。
将各参数带入式(1),求得接触应力σH=1021.24 MPa。
2.2 AGMA弯曲强度计算理论[2]
轮齿的弯曲强度与外齿轮齿根过渡圆弧处和内齿轮危险截面抗断裂的能力有关。标准中的弯曲强度计算基于平板理论,计算公式如下:
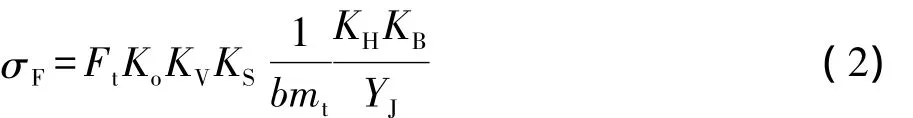
式中:轮缘厚度系数KB=1;弯曲强度几何系数YJ=0.404;端面模数mt=5 mm;将各参数带入式(2),计算得 σF=197.67 MPa。
3 基于Abaqus齿轮强度有限元分析
3.1 Pro/E 参数化建模[3]
(1)齿轮渐开线的生成
基本参数,在草图中绘画基圆、齿根圆、分度圆、齿顶圆四个基本几何部分,用从方程中-笛卡尔坐标系中输入以下命令,执行后得到一条渐开线,将其镜像,便得到一个齿的基本轮廓(如图1所示)。
ang=90*t
r=db/2s=pi*r*t/2
xc=r*cos(ang)
yc=r*sin(ang)
x=xc+s*sin(ang)
y=yc-s*cos(ang)
z=0
(2)齿轮的生成
加齿根圆角,形成完整轮廓,通过拉伸、轴向阵列完成齿轮模型,如图2所示。

图1 渐开线轮廓图

图2 齿形图
(3)齿轮副装配
在Pro/E中新建装配件,首先建立中心距,a=(25+80)×5/2=262.5 mm 的两个轴,将小齿轮和大齿轮添加装配,采用销钉约束方式,分别将两个齿轮的轴与所建立的两个轴重合,再将两个齿轮的端面对齐。转动一个齿轮调整近似啮合的位置,将标准操作界面切换至机构操作界面,利用凸轮命令,分别选择大小齿轮上需要啮合的某个齿面,进行无侧隙啮合(如图3所示),之后将配合好的模型进行全局干涉检查,干涉体积为0,整体装配成功。模型见图4。

图3 凸轮无侧隙啮

图4 整体装配图
3.2 利用Abaqus对齿轮进行力学分析[4-6]
(1)单元的属性与材料特性
将Pro/E中建好的三维模型保存成“.stp”格式,导入Abaqus。单元属性为三维实体单元,大小齿轮的材料均为40 Cr,其弹性模量为 E=2.06×105MPa,泊松比为 μ=0.3。
(2)网格划分
采用“扫掠”方法为齿轮划分六面体单元,单元类型为C3D8R。网格划分的越细,计算精度越高,但计算时间会相应增长,计算效率低。因此,将计算过程中有可能进入啮合的轮齿进行网格细化,非啮合轮齿划分较粗网格(如图5所示)。
(3)建立接触对
Abaqus中,接触类型有两种,即“面-面”接触与“点-面”接触。本文齿轮啮合时采用“面-面”接触类型。将计算过程中有可能进入啮合的轮齿建立接触对,其中大齿轮为接触面,小齿轮为目标面(如图6所示),摩擦系数为 0.1。
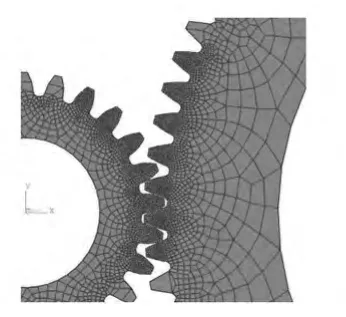
图5 网格划分
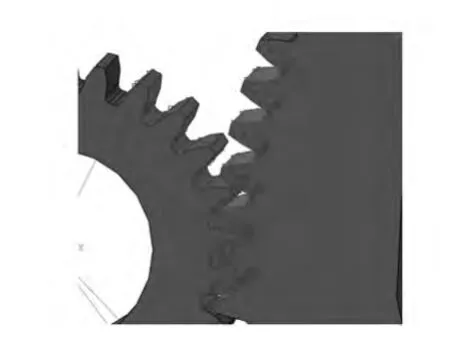
图6 确定接触面
(4)边界条件
本文计算时采用动态隐式分析方法,给小齿轮施加转角,大齿轮施加扭矩。在大齿轮圆心建立控制参考点RP-big,将该参考点与大齿轮内圈进行运动耦合;小齿轮圆心建立控制参考点RP-small,将该参考点与小齿轮内圈进行运动耦合(如图7所示)。
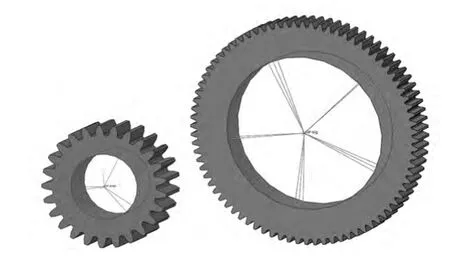
图7 运动耦合示意图
啮合过程中,使小齿轮旋转5个齿,根据小齿轮旋转速度,计算得到小齿轮的旋转角度0.754 rad。给小齿轮参考点RP-small施加沿Z轴的旋转位移UR3=0.754,约束其他五个方向的自由度(即U1=U2=U3=UR1=UR2=0)。
给大齿轮参考点RP-big施加沿Z轴的扭矩,大小为2617.6 N·m。约束其余五个方向的自由度(即U1=U2=U3=UR1=UR2=0)。
3.3 计算结果
接触强度计算结果:啮合过程中,当齿面接触在单齿啮合区时,齿面存在最大的接触应力,出现在齿轮节圆的位置,其值大小833 MPa(见图8所示)。
齿根弯曲强度计算结果:图9所示为小齿轮齿根应力云图,从图中可以看出,小齿轮齿根最大应力是172.8 MPa,啮合位置出现在小齿轮单齿啮合时轮齿的齿顶处,如图10所示。
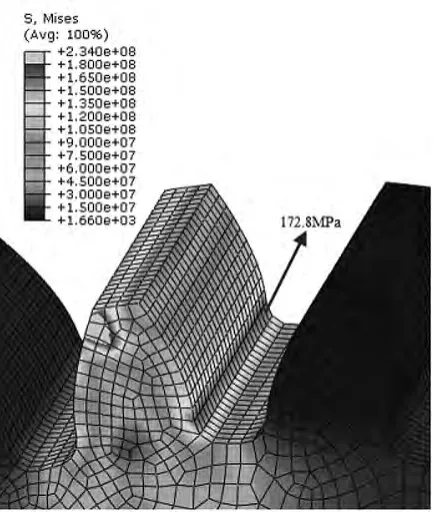
图9 小齿轮齿根弯曲应力云图
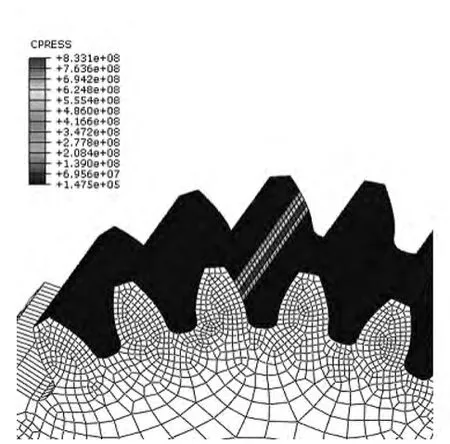
图8 接触应力
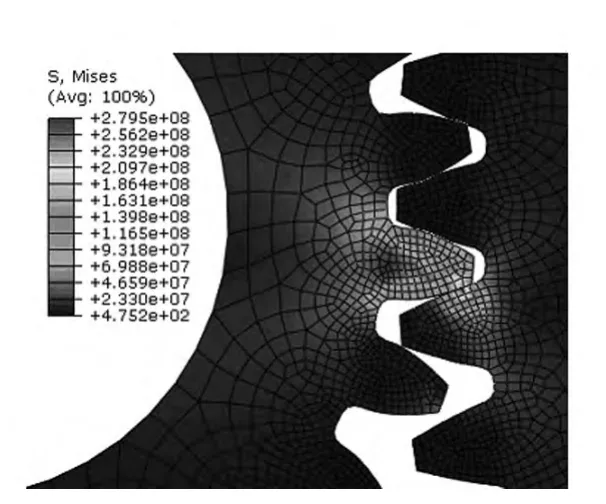
图10 最大弯曲应力啮合位置
4 结论
完成了Pro/E三维参数化建模方法生成模型,利用Pro/E凸轮机构的进行装配,可达到0干涉装配。理论计算标准是船级社认证的AGMA标准,接触强度理论计算值σH=1021.24 MPa。有限元计算最大值σ=833 MPa,发生在单齿啮合的节线处。弯曲强度理论计算值σF=197.67 MPa,有限元计算最大值σ=172.8 MPa,发生在单齿啮合齿根处。计算结果表明,采集到的应力值与传统理论计算的结果误差不大。理论计算偏于保守,结果可用于参考,而有限元分析可以得到较为准确的分析结果。有限元动态分析过程中,齿轮啮合过程中存在单齿啮合区和双齿啮合区,其过程应力分布情况也复杂多变。有限元直观的反映了啮合过程应力变化情况,为齿轮的进一步优化提供了理论基础。
[1] 王 钢,孟祥伟,彭 曼,等.自升式平台支撑升降系统结构设计与分析[J],机械设计,2011(7):42-45.
[2] ANSI/AGMA 2101-D04.Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth[S].
[3] 张 毅.基于Pro/E的斜齿轮建模和有限元分析[J].机械工程与自动化,2008(8):69-73.
[4] 唐进元,刘艳平.直齿面齿轮加载啮合有限元仿真分析[J].机械工程学报,2012(3):124-131.
[5] 赵 炜,葛文杰.ABAQUS/Python在斜齿轮动态啮合分析中的应用研究[J].研究开发,2012(7):29-31.
[6] 唐秀兰,杨华明.斜齿轮传动及相关分析[J].机械,2005(9):23-26.

