MIMO混合振动试验中正弦与随机信号分离方法
张步云, 陈怀海, 贺旭东
(南京航空航天大学振动工程研究所, 江苏 南京 210016)
引 言
振动环境试验作为检验产品可靠性与耐久性的有效手段,近半个世纪取得了长足的进展。多输入多输出振动试验比单轴振动试验更准确地模拟外场振动环境,能够克服单轴推力不足、量级不高、试验耗时较长等缺点,越来越受到研究者们的重视。在正弦、随机和冲击等振动试验研究中[1~6],人们已建立了成熟的理论体系,完善了先进的振动试验方法。国内外对相应的振动试验都制定了完整的试验标准与试验规范[7,8],使振动试验更具实用性与权威性。但已往的研究大都针对于某一单类振动试验的研究,而事实上工程机械或飞行器在运作过程中所经历的振动环境是相当复杂的。如直升机在飞行中由于浆片的旋转而产生一定频率的正弦振动,而引擎的工作则产生一个宽带的随机噪声。若用单一的正弦振动或随机振动来模拟机身所受的振动环境显然已经不准确,得到的试验结果不能用来作为飞机疲劳破坏的程度或损伤的判断标准。正弦加随机混合振动试验可以更好地完成对这种振动环境的模拟与再现,故其已成为振动试验研究的新课题[9,10]。
正弦振动试验中以信号的幅值与相位为控制对象,而随机振动试验则是通过闭环反馈将控制点的功率谱控制在给定的谱容差范围内。常用的正弦加随机控制方法是将正弦信号与随机信号分离后分别用已成熟的控制方法加以控制,再将反馈的控制信号叠加输送到振动台进行激振。正弦与随机信号分离的好坏将决定控制的精度,故其成为正弦加随机振动控制中最关键的环节。目前已有的分离方法有跟踪滤波法[11],将混合信号通过一比随机信号分析频率大很多的带通滤波器分离出正弦信号,此法高频分离尚可,低频的控制精度较差。王述成针对低频控制精度差的问题,提出了基于多分辨谱的控制方法[12]。借助维纳-辛钦定理从频域获取正弦信号的幅值,但频域识别存在能量泄露问题,不能保证控制的精度。Engelhardt提出用Vold-Kalman滤波器法[13],其分离方法比较复杂,且难以应用到振动试验控制之中。此外,还有计算法、截取法、复数二乘法和基于最小二乘法、盲分离等分离算法等[14~17]。这些方法运算复杂、计算量大,增加了控制回路的时间。
相关积分法可以有效地抑制测量噪声的影响,能提高测试信号的信噪比,是一种常用的信号处理方法。本文利用相关积分法的滤波特性,详细推导了正弦信号分离公式,有效分离了正弦与随机信号,提高了混合振动试验的控制精度。文中以一悬臂梁为仿真对象,验证了此方法的有效性。
1 多输入多输出混合振动控制
多输入多输出正弦加随机混合振动控制的整个流程如图1所示。先将混合参考谱分解为正弦参考值和随机功率谱,再将由实测信号分离得到的正弦值和实测随机信号的功率谱与参考谱进行比较,经过控制算法均衡后得到新的正弦信号和随机信号,将两者综合后输入激振器进行激振。如此循环,直到控制点的振动满足参考谱为止。
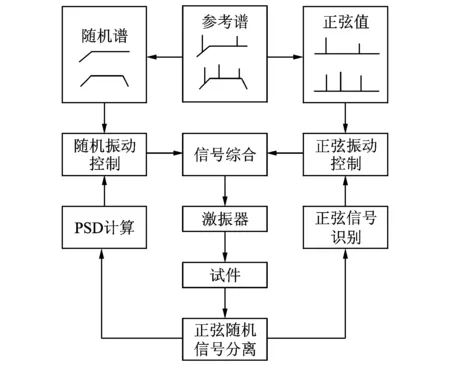
图1 正弦加随机混合振动控制流程
1.1 随机振动试验控制
频谱再现式随机振动试验是在较短的时间内“同时”激发给定功率谱谱形的宽带随机振动[17]。设参考谱为Sr(ω),根据振动理论,激励与响应的关系为
Sy(ω)=H(ω)Sx(ω)H*(ω)
(1)
式中Sy(ω)表示响应信号的功率谱密度,Sx(ω)表示激励信号的功率谱密度,H(ω)表示系统的频响函数矩阵,其上标*表示矩阵的共轭转置。为方便计,下文省略ω。随机振动试验的控制目标就是使Sy=Sr,则要求激励信号的功率谱满足
Sx=H-1Sy(H*)-1=ASrA*
(2)
式中A=H-1。对激励谱Sx和参考谱Sy分别进行Cholesky分解得
Sx=XX*,Sr=RR*
(3)
式中X,R均为下三角矩阵,将其带入式(2),由Cholesky分解的唯一性可得
X=AR
(4)
将X配以随机相位,进行逆FFT变换就可得到激励信号,再进行时域随机化便可得到纯随机激励信号。因系统中的非线性因素以及频响函数估计误差的存在,实际所测频响函数G并不是系统真正的频响,设它们的误差可用如下式表示
GA=I+ΔI
(5)
其中I为单位矩阵,ΔI为误差矩阵。则由式(4)所产生的激励信号所得到的响应谱为
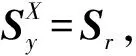
(I+ΔI)(ΔR)R((ΔR)R)*(I+ΔI)*=Sr
(7)
可计算出ΔR对角元素为
(8)
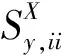
1.2 正弦振动试验控制
以某几个固定频率的正弦信号的叠加为激励,采集响应信号并进行幅值识别与参考值进行比较,计算出误差。然后反馈修正激励信号,使每个频率点的响应都能满足参考值的要求。一般正弦修正算法为
(9)
式中Ai表示当前驱动信号幅值,Ai-1表示前一次驱动幅值,E为前一次响应幅值与参考值的比,K表示压缩比,其大小影响响应信号收敛的速度。
假设初始响应信号与参考值之比为1.1,取不同的K观察响应收敛程度。分别取K为0.5,1,2,6,其收敛情况如图2所示。
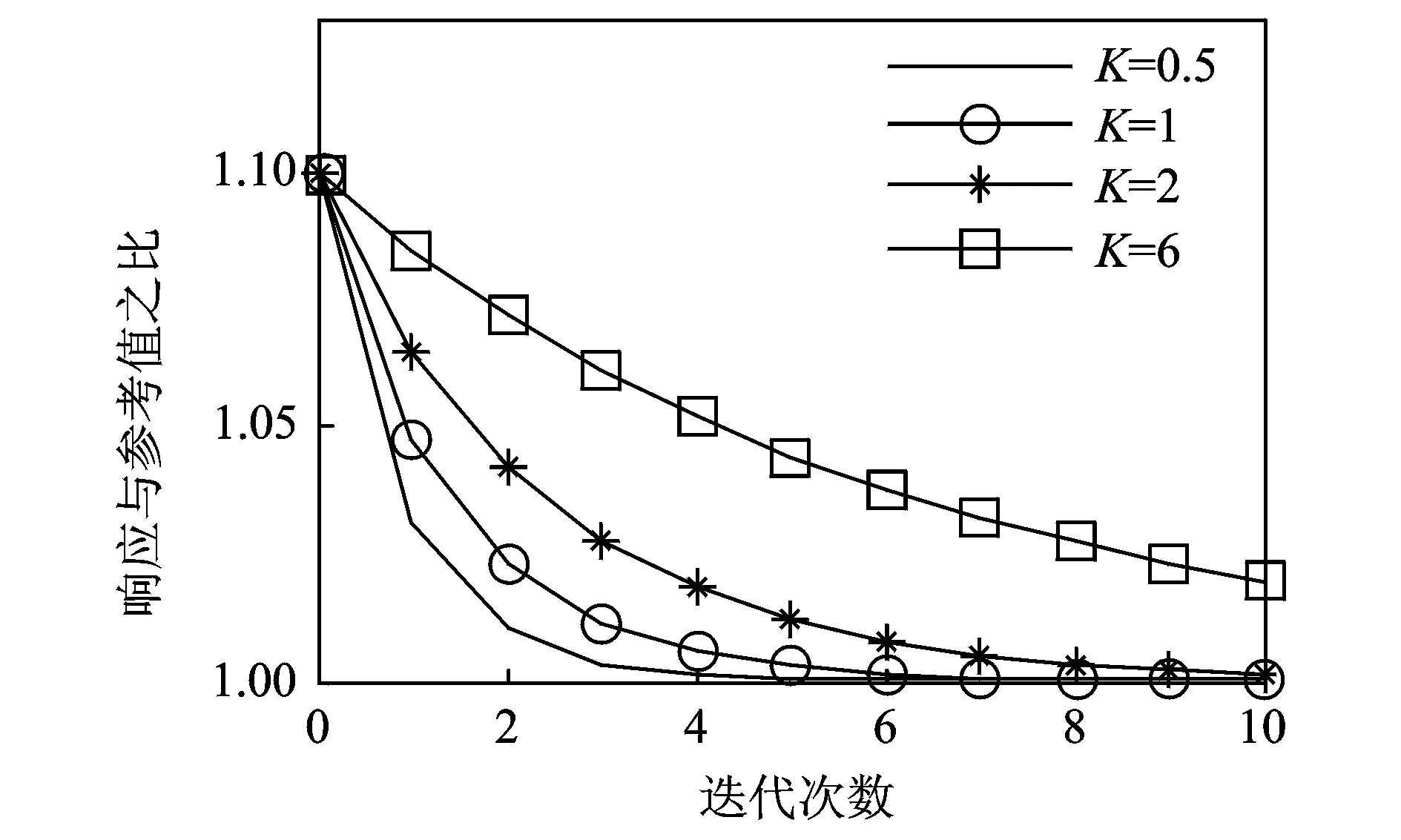
图2 压缩比K对收敛速度的影响
从图中可以看出收敛速度与K大小成反比,K取值越小,收敛速度越快。
2 混合信号中正弦分离
设正弦加随机混合信号可表示为如下形式
(10)
式中xr表示均值为零的平稳随机信号;混合信号中共含n个正弦信号,幅值为Ak,频率为ωk,相位为φk。因随机信号与正弦信号是相互独立的量,所以对任一频率的正弦函数,与随机信号xr有如下关系
(11)
在相关积分计算过程中,随机信号与正弦信号的计算是基于时间域的。它们乘积的相关积分函数不严格归零,但其积分值远低于原信号量级,可以忽略。式(10)与待识别频率正弦函数sin(ωpt)的相关积分函数为
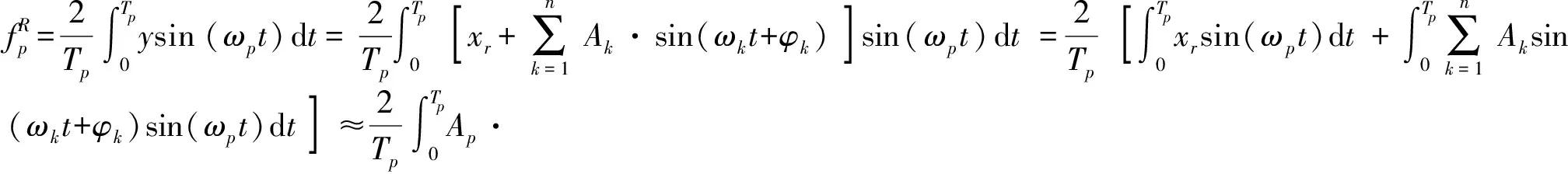
(12)
式中Tp表示sin(ωpt)的周期。同理,式(10)与待识别频率正弦函数cos(ωpt)的相关积分函数
(13)
由式(12)和(13)可以求得频率为ωp的正弦信号的幅值与相位为
(14)
按式(12)~(14)分别求出n个正弦信号,然后将其从混合信号中减掉,就可以很容易地得到随机信号
(15)
下面以某一直升机振动环境为研究对象,分析正弦信号与随机信号的分离。根据文献[8],可得该振动环境如图3所示。图中参数如表1所示。

表1 直升机振动环境参数
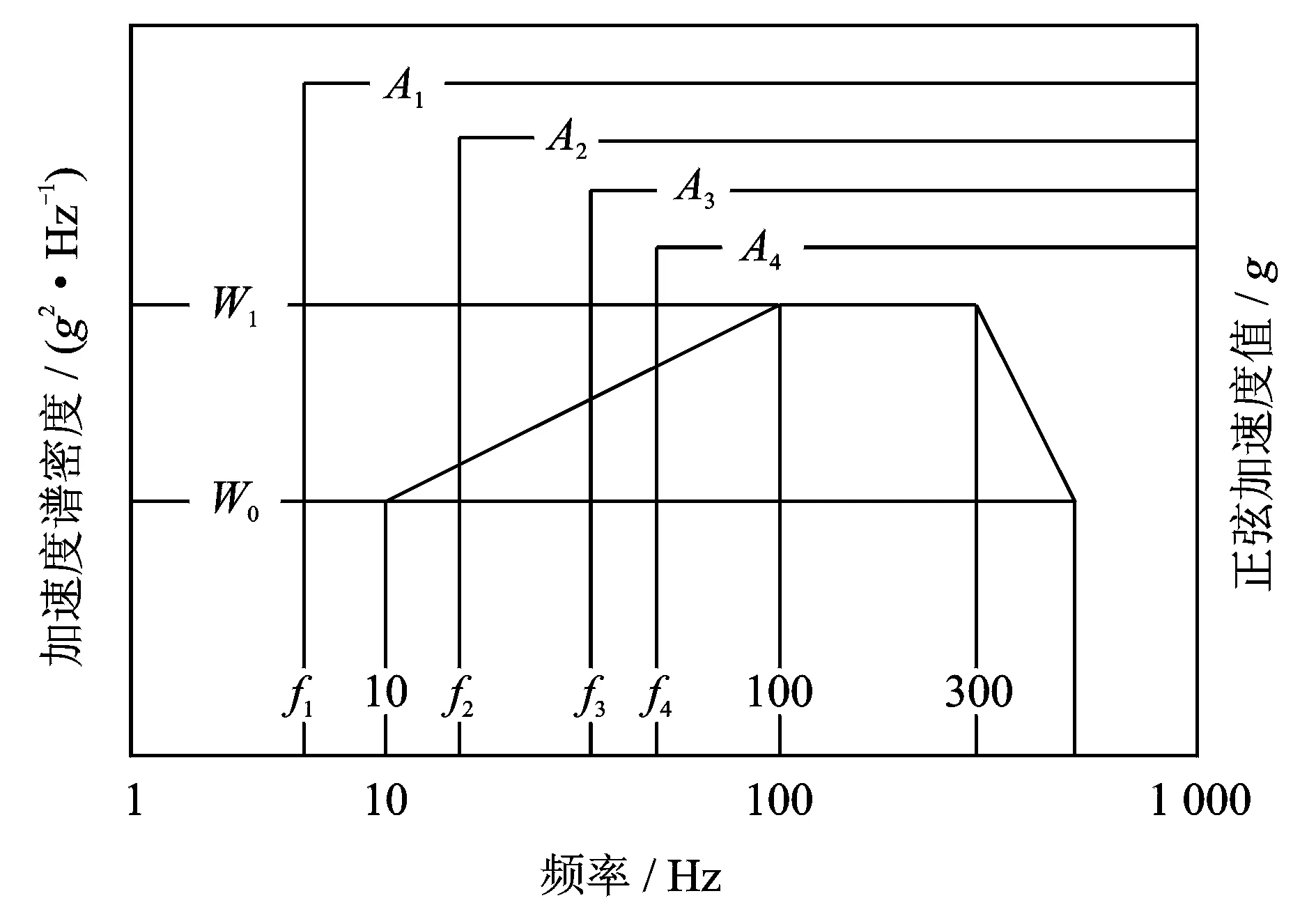
图3 某直升机振动环境
由表1和图3可以看出直升机的振动环境是由正弦振动和随机振动组合而成的。而且正弦的频率相对较低,以一个带宽为500 Hz的低量级随机振动作为振动背景。混合振动信号可以写成
(16)
由式(16)可得时域信号如图4所示。
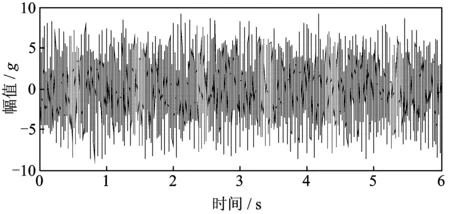
图4 混合时域信号
利用相关积分法和频域法同时识别式(16)中4个频率的正弦信号幅值,以比较两种方法识别精度的高低。频域法的识别流程是先对混合信号作FFT变换,然后根据维纳-辛钦定理获取正弦信号的幅值;再将两者识别的幅值同时与参考值作比较,计算出识别误差。经过计算,识别结果如表2所示。
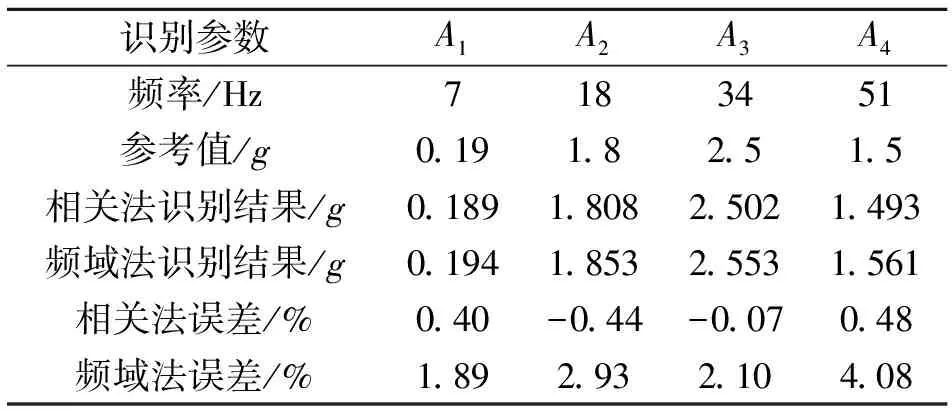
表2 正弦信号幅值识别误差分析
表2显示相关法识别正弦信号结果精度很高,绝对误差最高不足0.45%。而频域法识别结果误差很大,最少是相关法识别误差的4倍以上。固从表2可知,相关法识别的精度结果可进一步进行振动控制试验。
3 仿真算例
本文以一悬臂梁作为研究对象,进行两输入两输出混合振动随机控制仿真试验,模型尺寸及示意图见下图。用Matlab软件编制程序进行控制仿真试验,各阶阻尼比取0.03。
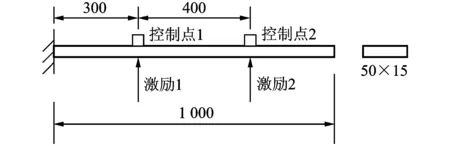
图5 试验模型尺寸及示意图 (单位:mm)
控制点的正弦成分如表1,而随机成分的参考谱如图6所示。
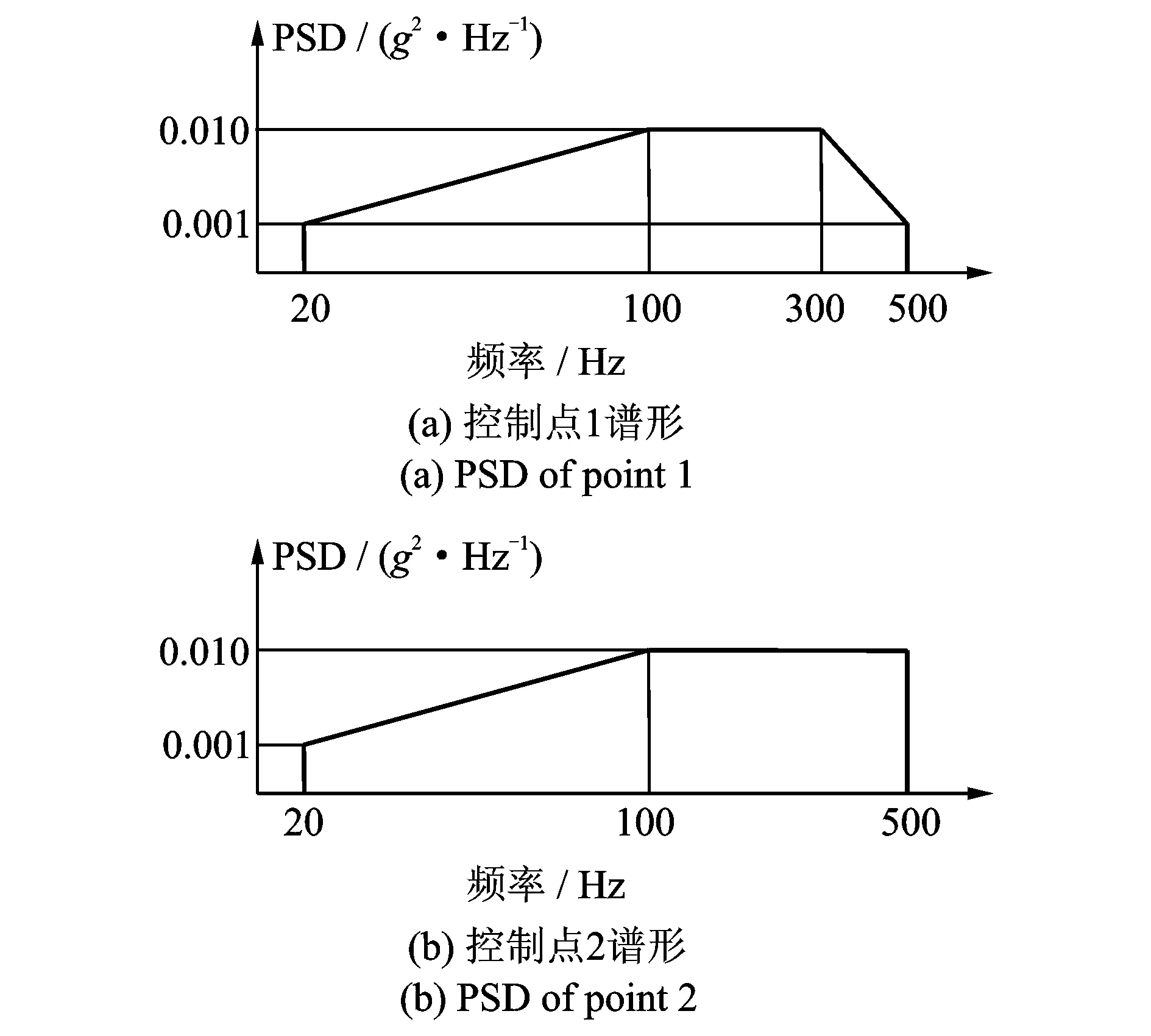
图6 控制点参考谱谱形
注意到式(2),在求驱动信号时须求频响的逆阵。在结构的反共振峰处,频响的幅值较小,甚至该频率处的矩阵是奇异的。若直接求逆阵,可能会发生病态,此时须求频响矩阵的广义逆H+。所以频响函数的准确估计成为振动控制的一个关键环节,本文采用快速正弦扫描法估计频响函数,此法能获得平谱,在整个测试频段内激励能量相同,信噪比大,能够提高估计精度。经过仿真计算,得到控制结果如分别如图7~10所示。
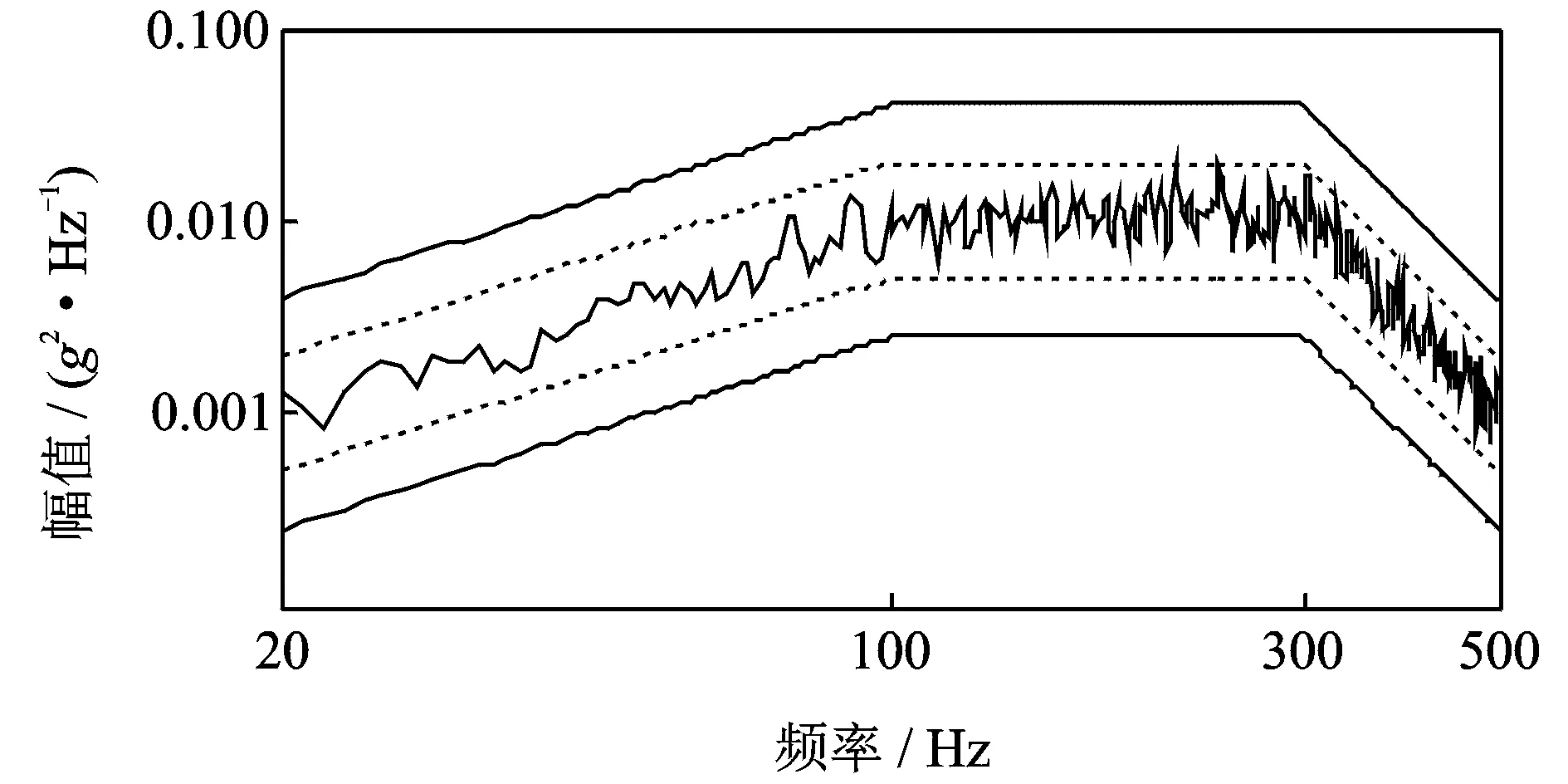
图7 控制点1随机振动控制结果
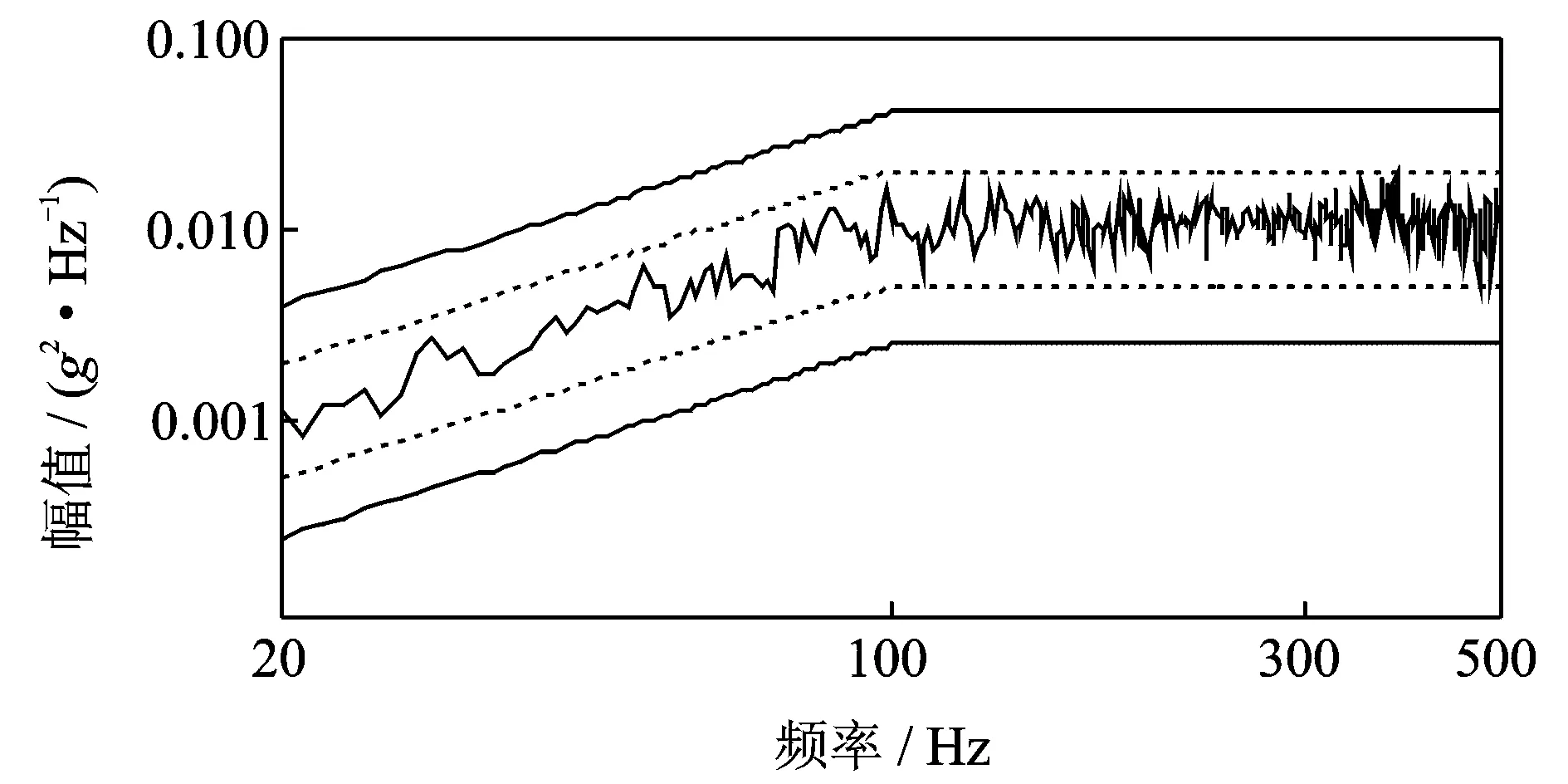
图8 控制点2随机振动控制结果
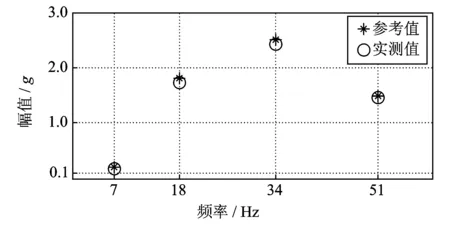
图9 控制点1正弦振动控制结果
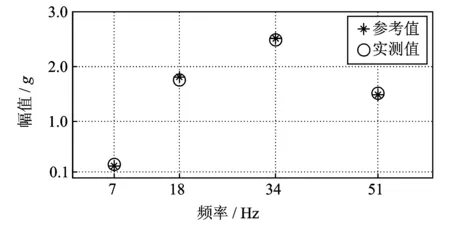
图10 控制点2随机振动控制结果
图7,8表示混合控制中随机振动的控制结果。图中虚线表示控制警告线,即参考谱的±3 dB值处;上下两条实线表示控制停止线,为参考谱的±6 dB值处。经过闭环反馈控制,可以从图中看出两点的响应谱都被控制在警告线以内。控制点1和2参考谱的总均方根值分别为1.77g和2.1g,而图7,8中两点响应谱的总均方根值为1.78g和2.15g,误差分别为0.6%和2.4%。综前,随机控制满足控制要求。
图8,9表示正弦振动控制结果。混合振动中含有4个定频振动,频率分别为7,18,34和51 Hz,以正弦加速度(g)为控制对象。从图中可以看出,正弦幅值控制误差满足工程要求,即可以实现振动控制。
4 结 论
本文将相关积分法运用到随机加正弦混合振动试验中,利用其滤波特性将随机信号与正弦信号精确分离,从而分别进行随机振动控制和正弦振动控制,解决了混合振动控制中的关键问题。通过建立两输入两输出振动控制系统,利用Matlab软件编制控制程序,对系统进行混合控制。仿真结果表明:随机振动信号被控制在参考谱的±3 dB以内,正弦信号幅值被控制在参考值的±10%以内,实现了良好的控制效果。
参考文献:
[1] Underwood M A. Adaptive control method for multi- exciter sine tests[P]. USA: US5299459 A, 1994,4,5.
[2] Smallwood D O. Multiple shaker random vibration control-an update[R]. Institute of Environmental Sciences and Technology (IEST) Annual Meeting, SAND98 -2044C, USA, US Department of Energy,1999:212—221.
[3] 贺旭东,陈怀海.一种多点随机振动试验控制的新方法研究[J].振动工程学报,2004,17(1):49—52.He X D, Chen H H. A new method for the control of multi-shakers in random vibration tests[J]. Journal of Vibration Engineering, 2004,17(1):49—52.
[4] 崔旭利,陈怀海,贺旭东,等.全相位Hv频响函数估计在MIMO随机振动试验中的应用[J].振动工程学报,2011,24(2):181—185.Cui X L, Chen H H, He X D, et al. All-phase Hvfrequency response function estimation for MIMO random vibration test control[J]. Journal of Vibration Engineering, 2011,24(2):181—185.
[5] Baren J V. What is random vibration testing[J]. Sound and Vibration, 2012,2:9—12.
[6] Underwood M A. Apparatus and method for adaptive closed loop control of shock testing system[P]. USA: US5517426A, 1996,5,14.
[7] Department of Defense of United States of America. MIL-STD-810G-2008[S]. Environmental engineering conside- rations and laboratory tests.
[8] 中国人民解放军总装备部.GJB 150.16A-2009.军用装备实验室环境试验方法第16部分: 振动试验[S].Chinese PLA General Armament Department. GJB 150.16A-2009. Laboratory environmental test methods for military materiel, Part 16: Vibration Test[S].
[9] 孙成宽.多输入多输出随机加正弦振动控制系统的研究[D].南京:南京航空航天大学,2010.Sun C K. Research on MIMO sine on random vibration control system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.
[10] 上海市质量监督检验技术研究院. GB/T 2423.58-2008,电工电子产品环境试验.第2-80部分:试验方法.试验Fi:振动.混合模式[S].北京:国家质检总局, 2009.Shanghai Institute of Quality Inspection and Technical Research. GB/T 2423.58-2008, Enviromental testing for electric and electonic products. Part2: Tests methods. Test Fi: Vibration. Mixed Mode[S]. Beijing: CN-GB, 2009.
[11] 袁宏杰,李传日.正弦加随机振动控制技术的研究[J].航空学报,2000,21(4):383—384.Yuan H J, Li C R. Study on the sine-on-random vibration control[J]. Acta Aeronautica et Astronautica Sinica, 2000,21(4):383—384.
[12] 王述成,陈章位.基于多分辨谱分析的正弦加随机振动试验控制算法的研究[J].中国机械工程,2005,16(15):1 335—1 338.Wang S C, Chen Z W. A new algorithm for sine on random vibration test based on multirate spectrum estimation[J]. China Mechanical Engineering, 2005,16(15):1 335—1 338.
[13] Engelhardt C, Baker M, Mouron A, et al. Separation of sine and random components from vibration measurements[J]. Sound and Vibration, 2012,6:6—11.
[14] 龚庆祥,陈应汀.频率分析中正弦和随机的分离与判辨[J].洪都科技,1979,4:1—6.Gong Q X, Chen Y T. Separation and analysis of sine and random signals in the frequency analysis[J]. Hongdu Technology, 1979,4:1—6.
[15] 袁宏杰,李传日. VCS振动控制系统控制算法研究[J].仪器仪表学报(S), 2002,23(3):846—847.Yuan H J, Li C R. VCS vibration control system control algorithm[J]. Chinese Journal of Scientific Instrument (S), 2002,23(3):846—847.
[16] 江勇,张林柯,何琳,等.两次去相关用于振动信号盲分离[J].振动、测试与诊断,2011,31(2):241—245.Jiang Y, Zhang L K, He L, et al. Blind separation of vibration signals using double decorrelation[J]. Journal of Vibration, Measurement & Diagnosis, 2011,31(2):241—245.
[17] 胡志强.随机振动试验应用技术[M].北京:中国计量出版社,1998:118.Hu Z Q. Application Technology of Random Vibration Test[M]. Beijing: China Metrology Publishing House, 1998:118.
[18] 贺旭东,陈怀海,申凡,等.双振动台随机振动综合控制研究[J].振动工程学报,2006,19(2):145—149.He X D, Chen H H, Shen F, et al. Study on dual-shaker random vibration test control[J]. Journal of Vibration Engineering, 2006,19(2):145—149.

