大加减速轴向移动系统的振动控制
刘 屿, 翁 轩, 吴忻生, 刘伟东
(华南理工大学自动化科学与工程学院,广东 广州 510640)
引 言
轴向移动结构被广泛的应用于高速高精度电子制造装备。然而装备中轴向移动结构的弹性变形将产生振动现象,振动则是在时间和空间尺度方面都将直接制约装备的生产性能[1,2]。因此,如何快速地消除精密电子制造装备中轴向移动结构的振动现象,已成为制约精密电子制造,特别是集成电路(IC)封装工序的瓶颈问题。
轴向移动结构是一类具有强耦合、非线性和无穷维的典型分布参数系统,因此对其控制策略设计具有很大的难度,传统的控制方法大多采用降阶模型进行控制设计,但仅对几个关键模态进行控制时,未建模高频模态有可能导致溢出效应,从而影响系统的稳定性;同时若需提高控制精度,则控制器阶数也将随柔性模态的增加而增加,因此从工程角度很难实现[3,4]。边界控制因其能避免控制溢出和易构造Lyapunov函数等独特优势而非常适合柔性结构的振动主动控制[5~7]。近年在轴向移动结构振动控制方面的研究成果将边界控制、自适应和Lyapunov直接法等相结合[8~11],基于结构无限维模型直接进行振动主动控制设计,取得较好效果并避免了溢出问题。然而,目前国内外研究成果都假设轴向移动结构的运动为匀速运动,这显然只考虑了其中最为简单的运动方式,因为绝大多数轴向移动结构的运动不仅是变速运动,通常还是大加减速和高速运动,结构具有很强的几何非线性特性[12]。因此,目前国内外关于轴向移动结构的动力学模型以及振动主动控制方法都很难适用于大加减速轴向移动结构的振动控制。
传统的直线/指数加减速在系统启动和结束时存在加速度突变,易产生冲击,柔度差。而S曲线加减速通过对启动阶段加速度的衰减来保证电机的性能和减小冲击,具有较好的柔度,因此在高速高精密电子制造装备中得到广泛的应用。表面贴装技术(SMT)中的轴向移动结构具有典型的大加减速特征,其最大加速度通常达到5g以上(g为重力加速度),其结构振动呈现出复杂的动态特性。本文以作者所在团队自主研发SMT中轴向移动结构为研究对象,建立其包含结构几何非线性特性的动力学模型,并基于该无限维分布参数模型,采用Lyapunov直接法和S曲线加减速法,设计边界控制算法对大加减速轴向移动系统的振动进行主动控制,从而抑制其振动,提高装备的加工精度。其后基于设计的控制算法,证明了控制系统的稳定性和一致有界性。最后给出了所设计控制器的有效性和可靠性仿真研究结果。
1 轴向移动系统动力学模型
在本文中,做如下简写假设:φ(·)(x,t)=(·), (·)x=∂(·)/∂x, (·)t=∂(·)/∂t。
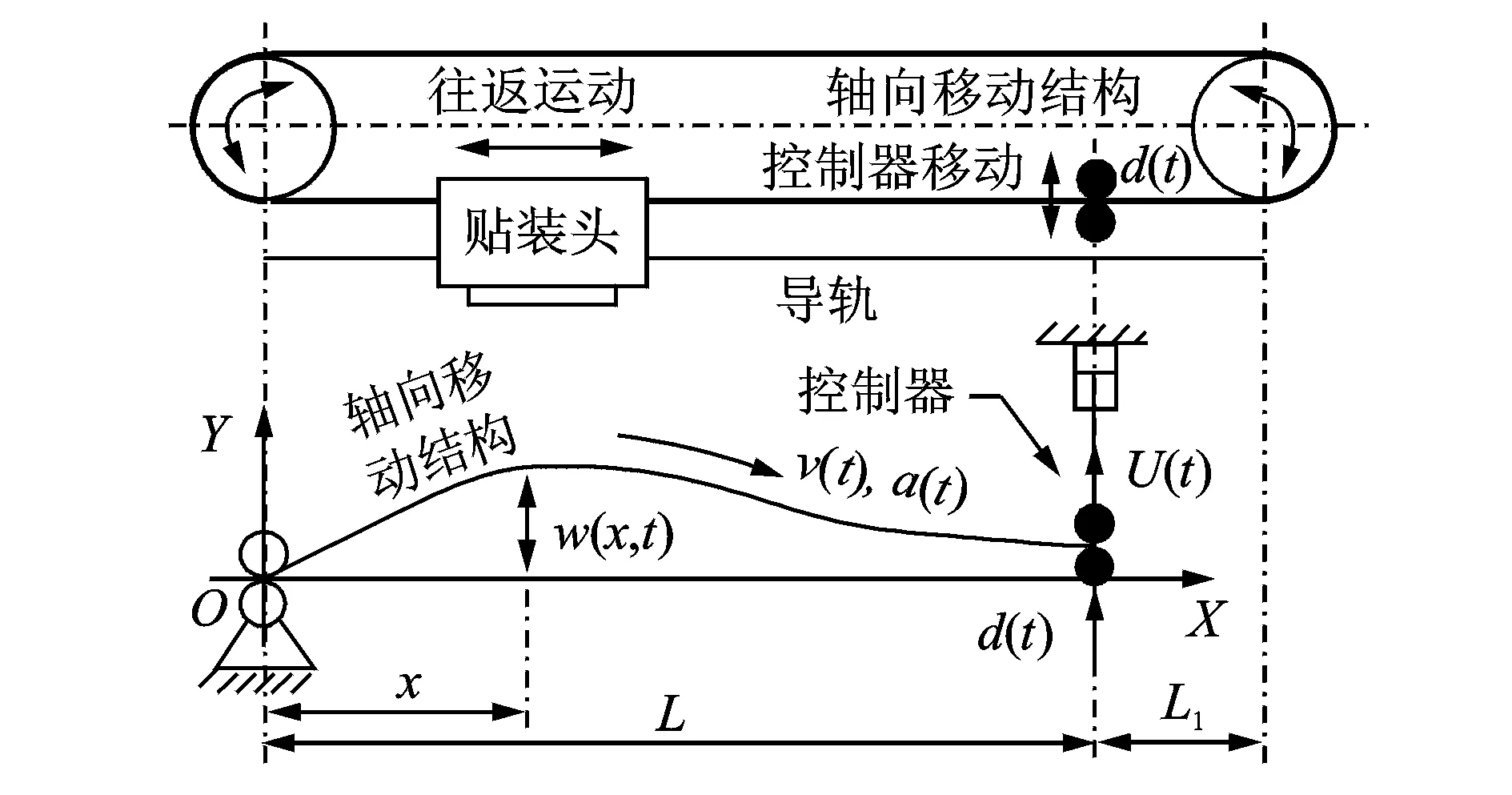
图1 贴片机(SMT)中典型的轴向移动系统
图1为SMT中典型轴向移动系统。坐标系原点O位于其左轮端,借鉴文献[13]的处理方式,将整个轴向移动结构划分为控制段L和未控制段L1,控制输入U(t)作用于控制段L的右端,且方向向上,未控制段的振动对控制系统的影响视为末端扰动d(t)作用于控制器,w(x,t)为t时刻在轴向移动结构位置x处的偏移量。
轴向移动系统的运动方程可由广义Hamilton原理表示为[14]
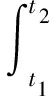
(1)
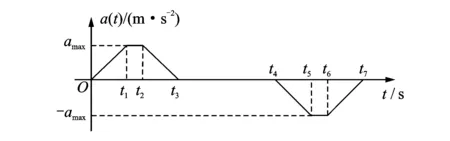
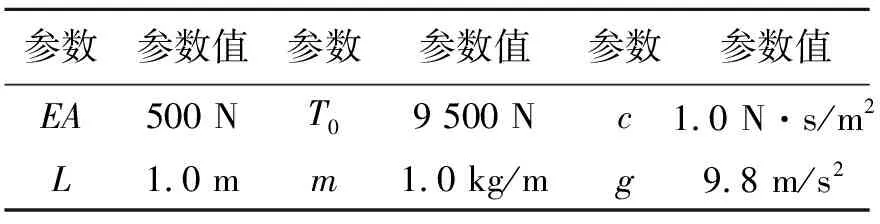
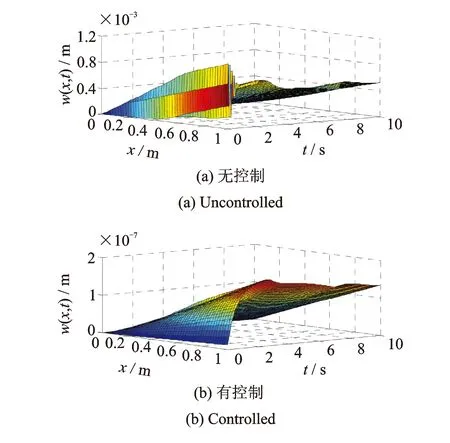
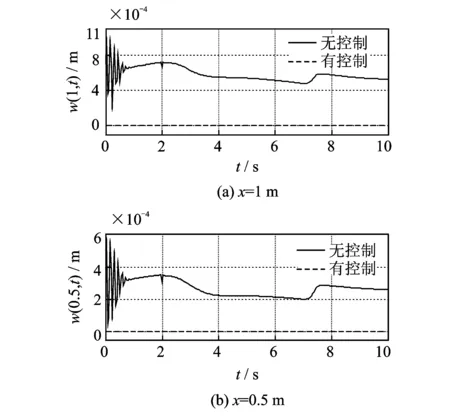
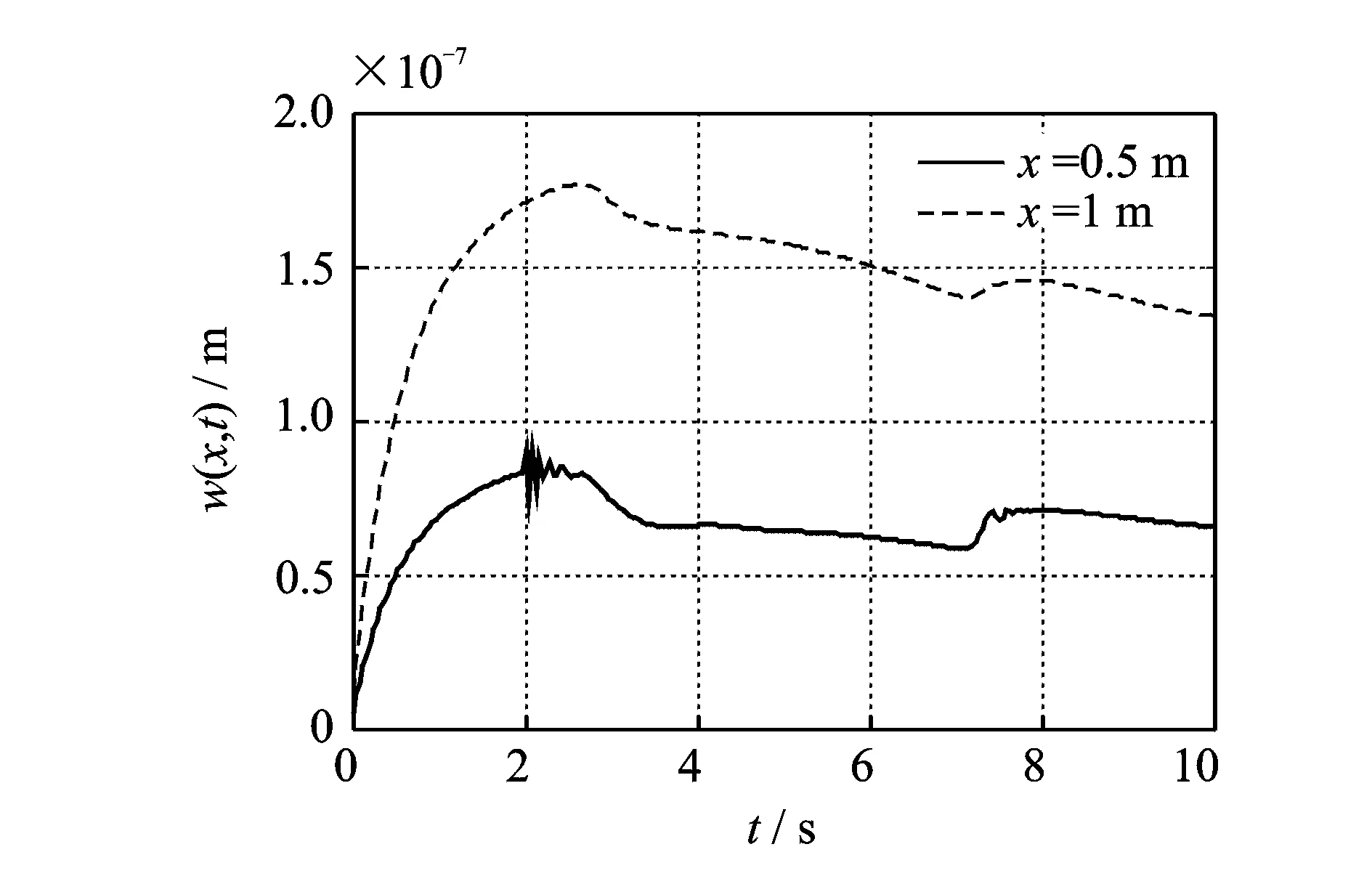
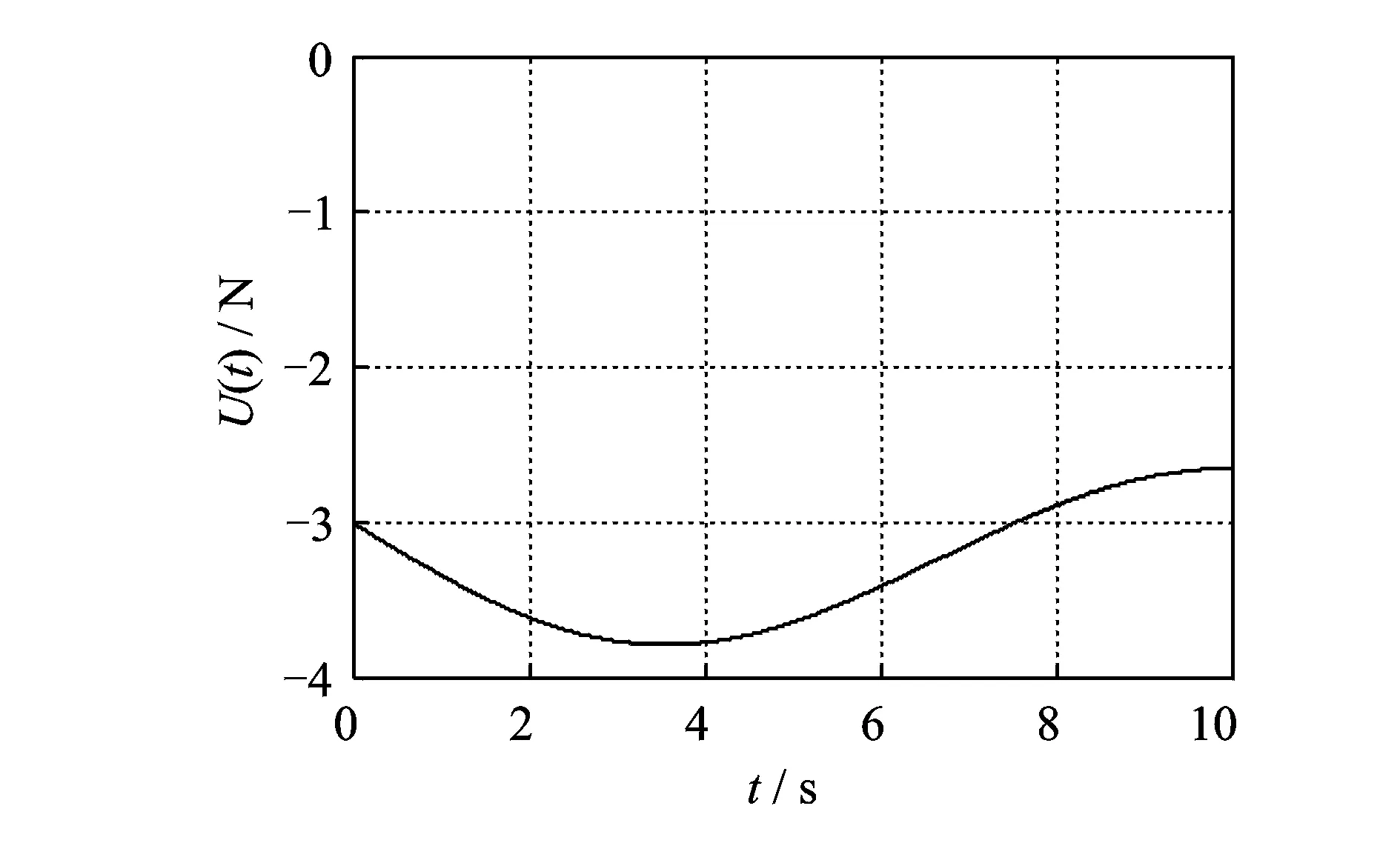
式中δ为变分操作符,t1和t2为两时刻,t1 轴向移动结构的动能Ek可表示为 (2) 式中m为结构单位长度质量,速度v(即v(t))为 v=v0+at (3) 式中v0为初始速度,a(即a(t))为加速度。 轴向移动结构的势能Ep可表示为 (4) 式中 结构的变张力T可表示为[10] (5) 式中 常数T0为结构未扰动情况下的张力。 描述位移-应变关系的ε可表示为 (6) 结构右边界非保守力所做虚功δWc可表示为 (7) 式中 常数c为轴向移动结构的粘性阻尼系数,U和d分别为U(t)和d(t)的简写。 结构右边界处的虚拟动量δWb可表示为 δWb=mv[wt(L,t)+vwx(L,t)]δw(L,t) (8) 将式(2),(4),(7)和(8)带入式(1)中,并应用变分和分部积分可得轴向移动系统的控制方程 2mvwxt+mv2wxx+cwt+cvwx=0 (9) 其中∀(x,t)∈(0,L)×[0, +∞)。 则轴向移动系统的边界条件为 (10) 其中∀t∈[0, +∞)。 假设1对于结构运动速度v(t)、加速度a(t)和末端扰动d(t),若存在常数a1,a2,a3∈R+,使得0≤v(t)≤a1, |a(t)|≤a2, |d(t)|≤a3, ∀t∈[0,+∞)。该假设是合理的,因为v(t)和d(t)为具有有限能量的连续函数,因此它们是有界的[8~10]。 为了抑制轴向移动结构因末端未知扰动引起的振动,本文利用Lyapunov直接法在结构右边界构造一个边界控制器,通过控制器的控制作用减小轴向移动结构的振动偏移量。 引理1若φ1(x,t),φ2(x,t)∈R,σ>0其中x∈[0,L],t∈[0, +∞),则有[5~7] (11) 引理2若φ(x,t)∈R为在(x,t)∈[0,L]×[0, +∞)的函数,且满足边界条件[5~7] φ(0,t)=0, ∀t∈[0,+∞) (12) 则有 (13) 若取Lyapunov函数为 V(t)=V1(t)+V2(t)+V3(t) (14) 其中能量项V1(即V1(t))为 (15) 其中交叉项V2(即V2(t))为 (16) 其中附加项V3(即V3(t))为 (17) 其中γ,λ,k2,k3>0。 引理3由式(14)定义的Lyapunov函数具有如下上下界 0≤ϑ1(V1+V3)≤V≤ϑ2(V1+V3) (18) 其中ϑ1,ϑ2>0。 证应用不等式(11)~(13),由式(16)可得 (19) 将上不等式改写为 -ξV1≤V2≤ξV1 (20) 若适当的选取ξ,可以得到 (21) 将不等式(21)分别带入式(20)可得 0<ξ1V1≤V1+V2≤ξ2V1 (22) 结合Lyapunov函数式(14),由式(22)可得 0≤ϑ1(V1+V3)≤V≤ϑ2(V1+V3) (23) 其中ϑ1=min[ξ1, 0.5(λk2+γk3)]>0,ϑ2=max[ξ2, 0.5(ϑk2+ϑk3)]>0。证毕。 引理4由式(14)定义的Lyapunov函数的时间导数具有如下上界 Vt≤-ϑV+ε (24) 其中ϑ,ε>0,V为V(t)简写。 证将式(14)对时间求导有 Vt=V1t+V2t+V3t (25) 其中由式(15)可得 V1t=A1+A2+A3+A4 (26) 将式(9)带入A1的表达式,并应用分部积分得 (27) 对A2和A3的表达式进行分部积分可得 (28) 将式(27)~(28)和A4的表达式带入式(26)中,再结合系统边界条件式(10)和不等式(11)~(13)有 (29) 式中δ1为任意正常数。 将式(16)对时间求导可得 V2t=B1+B2+B3 (30) 对式B1进行分部积分可得 (31) 将式(9)带入B2的表达式,并应用分部积分可得 (32) 将式(31)~(32)和B3代入式(30),并结合系统边界条件式(10)和不等式(11)~(13)有 (33) 式中δ2,δ3,δ4,δ5为任意正常数。 将式(17)对时间求导可得 V3t=(λk2+γk3)w(L,t)wt(L,t) (34) 分别将式(29),(33)~(34)带入式(25)中可得 (λk2+γk3)w(L,t)wt(L,t)+λdw(L,t)+ (35) 若设计边界控制器为 U=-k1wx(L,t)-k2wt(L,t)-k3w(L,t) (36) 式中k1为正的比例系数。 将边界控制器(36)带入式(35),并结合不等式(11)~(13)有 -ϑ3(V1+V3)+ε (37) 式中δ6,δ7为任意正常数。当选择适当的参数值γ,λ,k1~k3,δ1~δ7满足如下条件: τ6=γc+λm-λcδ4-2λmaδ5>0,τ7=2λc+γc-λm>0,τ8=2γc+2λc-2λm>0, λdw(L,t)+γdwt(L,t)|, 由不等式(37)和不等式(23)可得 Vt≤-ϑV+ε, (38) 其中ϑ=(ϑ3/ϑ2)。证毕。 边界控制器式(36)中的w(L,t)和wx(L,t)可分别由位移和倾角传感器测得,由w(L,t)后向差分算法计算可得到wt(L,t)。此控制器设计不需知道扰动量的精确模型,因此对系统参数的变化具有稳定鲁棒性。 定理1由式(9)~(10)所描述的大加减速轴向移动系统,在假设1条件和控制器式(36)作用下有: 1) 一致有界:闭环轴向移动结构的振动偏移状态量w(x,t)∈R一致包含于紧集Ω1中 Ω1∶={|w(x,t)|≤χ1} (39) 2) 一致最终有界:闭环轴向移动结构的振动偏移状态量w(x,t)∈R最终收敛于紧集Ω2中 (40) 证对式(38)乘以eϑt,可得 (41) 对上述不等式积分得 (42) 其中上式表明V有界。 由不等式(13)、等式(15)和不等式(18)可得 (43) 重排不等式(43),并将式(42)带入有 (44) 其中∀(x,t)∈[0,L]×[0, +∞),则进一步可得 (45) 由式(44)和(45)可知定理1得以证明。证毕。 本节数值仿真研究轴向移动系统在扰动作用下的振动情况,并验证所设计边界控制算法式(38)的有效性。图2给出了本文所使用的S曲线加减速法示意图, 表1为轴向移动系统的详细参数。 图2 S曲线加减速法示意图 图中amax=3.5g,g为重力加速度,时间坐标为[t1,t2,t3,t4,t5,t6,t7]=[1, 2, 3, 7, 8, 9, 10]。 表1 轴向移动系统参数 轴向移动系统的初始条件为 w(x,0)=wt(x,0)=0 (46) 末端扰动d(t)为 (47) 当选择边界控制器参数k1=k2=k3=1×107, 图3~6给出了数字仿真结果,其中图3为轴向移动结构分别在有、无控制作用下的振动偏移量,图4则具体给出了结构中部(x=0.5 m)和右端处(x=1 m)的振动偏移图,图5给出了在边界控制作用下,结构中部和右端处的振动偏移对比图, 图6则给出的是边界控制输入。由上述仿真结果可得出如下结论: 1)由仿真结果图3,4可知,当边界控制输入作用于大加减轴向移动结构后,结构的振动偏移量都有数千倍的减少,验证了本文设计的边界控制算法对抑制结构的振动是非常有效的; 2)由仿真结果图4,5可知,虽然在轴向移动结构中部(x=0.5 m)处未布置边界控制器,但在边界控制输入作用下,结构中部的振动也有非常显著的减小,体现了边界控制技术在柔性结构振动控制方面的独特优势; 图3 轴向移动结构偏移量 图4 轴向移动结构偏移量 图5 控制作用下轴向移动结构偏移量 3)由仿真结果图4,5可知,因为大加减速的改变直接冲击轴向移动结构速度和动力学特性,从而影响结构的振动偏移量,特别在t=2 s和t=7 s左右尤为明显。 4) 由仿真结果图6可知,边界控制输入范围为2.5~4 N,而负值表示控制作用力与外部干扰方向相反。 5) SMT中轴向移动结构振动的有效控制,将直接减小结构振动幅值,对提高制造装备特别是精密电子制造装备的加工精度具有十分重要意义。 图6 边界控制输入 本文研究了具有大加减速轴向移动结构在外部干扰作用下的振动主动控制问题。基于结构几何非线性特性和Hamilton原理建立了结构无穷维分布参数模型,采用Lyapunov直接方法,在结构右边界设计了边界控制器用以抑制结构振动,仿真结果表明研究取得很好的结构振动控制效果。本文所设计边界控制器除了能避免控制溢出问题,还具有较强的鲁棒性。利用Lyapunov直接法对控制系统的稳定性和有界性给予了验证。本文研究成果对精密电子制造装备中大加减速轴向移动结构的振动控制具有理论和实际指导意义。 参考文献: [1] Nguyen Q C, Hong K S. Simultaneous control of longitudinal and transverse vibrations of an axially moving string with velocity tracking[J]. Journal of Sound and Vibration, 2012, 331(13):3 006—3 019. [2] 王亮, 陈怀海, 贺旭东, 等. 轴向运动变长度悬臂梁的振动控制[J]. 振动工程学报, 2009,22(6):565—570.Wang Liang, Chen Huai-hai, He Xu-dong, et al. Vibration control of an axially moving cantilever beam with varying length[J]. Journal of Vibration Engineering, 2009,22(6):565—570. [3] Balas M J. Feedback control of flexible systems[J]. IEEE Transactions on Automatic Control, 1978,23(4):673—679. [4] Meirovitch L, Baruh H. On the problem of observation spillover in self-adjoint distributed systems[J]. Journal of Optimization Theory and Applications, 1983,39(2):269—291. [5] Liu Y, Huang H W, Gao H X, et al. Modeling and boundary control of a flexible marine riser coupled with internal fluid dynamics[J]. Journal of Control Theory and Applications, 2013,11(2):316—323. [6] 刘屿, 黄浩维, 邬依林, 等. 基于Lyapunov直接法的柔性梁振动控制[J]. 华南理工大学学报(自然科学版), 2013,41(2):24—29.Liu Yu, Huang Hao-wei, Wu Yi-lin, et al. Vibration control of flexible beam based on Lyapunov direct method[J]. Journal of South China University of Technology (Natural Science Edition), 2013,41(2):24—29. [7] 邬依林, 刘屿, 吴忻生. 基于时变内流的柔性立管自适应边界控制[J]. 控制理论与应用, 2013,5(30):618—624.Wu Yi-lin, Liu Yu, WU Xin-sheng. Adaptive boundary control of a flexible riser coupled with time-varying internal fluid[J]. Control Theory & Applications, 2013, 5(30): 618—624. [8] Nguyen Q C, Hong K S. Asymptotic stabilization of a nonlinear axially moving string by adaptive boundary control[J]. Journal of Sound and Vibration, 2010,329(22):4 588—4 603. [9] Li Y G, Aron D, Rahn C D. Adaptive vibration isolation for axially-moving strings: theory and experiment[J]. Automatica, 2002,38(3):379—390. [10] Qu Z H. Robust and adaptive boundary control of a stretched string on a moving transporter[J]. IEEE Transactions on Automatic Control, 2001,46(3):470—476. [11] 张伟, 陈立群. 轴向运动弦线横向振动控制的Lyapunov方法[J]. 控制理论与应用, 2006,23(4):531—535.Zhang Wei, Chen Li-qun. Transverse vibration control of an axially moving string system by Lyapunov method[J]. Control Theory & Applications, 2006,23(4):531—535. [12] Chung C, Han C S, Yi K. Vibration of an axially moving string with geometric non-linearity and translating acceleration [J]. Journal of Sound and Vibration, 2001,240(4),733—746. [13] Yang K J, Hong K S, Matsuno F. Energy-based control of axially translating beams: varying tension, varying speed, and disturbance adaptation[J]. IEEE Transactions on Control Systems Technology, 2005,13(6),1 045—1 054. [14] Goldstein H, Poole C P, Safko J L. Classical Mechanics[M]. 3rd Edition, New York: Addison Wesley Press, 1951.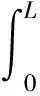
2 控制器设计
2.1 预备知识
2.2 边界控制器
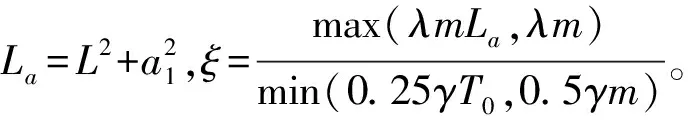
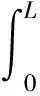
2.3 稳定性分析
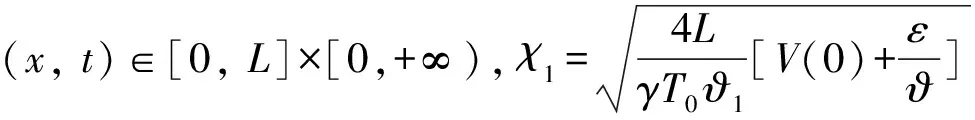
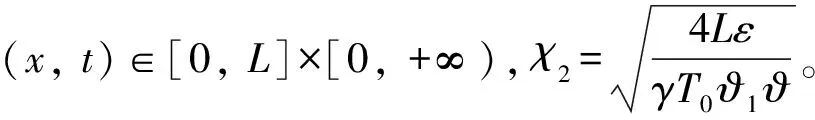
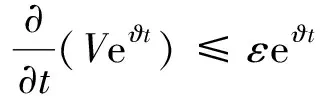
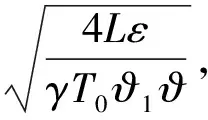
3 仿真分析
4 结 论

