双自由度压电振动能量采集器的力-电输出特性分析
展永政, 王光庆
(浙江工商大学信息与电子工程学院,浙江 杭州 310018)
引 言
便携设备和无线传感器使用传统电池供电,这种电池不仅供能寿命有限、需要频繁更换[1,2],还引起环境污染。能量采集器通过从周围环境(如风能、热能和振动等)获取能量,向超低功率的微处理设备供电。振动能量采集器由于成本低和高功率等特点引起研究者的兴趣。目前,振动机电转换机制主要通过静电、电磁和压电三种机制来实现[3~5],其中,压电式振动能量采集器(Piezoelectric vibration energy harvester, 简称PVEH)转换电能时不需要额外的功率,还具有易制作,简易机电结构和高功率密度等优点。因此,压电振动能量采集器成为微能源研究领域的热点。
传统压电振动能量采集器由压电双晶片或压电单晶片悬臂梁构成,它是单自由度系统(Single-degree-of-freedom,简称SDOF)。虽然这种压电振动能量采集器能够在谐振状态下输出高功率,但是激发条件易受环境影响,难于保证在谐振时刻输出高功率。因此,为了提高压电振动能量采集器的能量转换效率,必须研究宽频压电采集技术,使压电振动能量采集器在一定的频率范围内产生谐振或近似谐振。Liao和Sodano采用了优化参数的方法来建立数学理论模型以拓宽频率,但是忽略了能量采集器内部阻抗与最优负载阻抗的关系,不能准确地表明输出功率最大化的本质[6]。Challa和Wu等利用调整频率的方法对宽频进行了研究[7,8],但是这种情况只能工作于频率变化缓慢的情况下,对频率调节器的精度要求更高,且智能型微调节器难以实现。另外,Ma引进动态放大器建立数学模型来研究宽频压电振动能量采集器,但忽略了能量采集器的机电耦合效应[9]。Aldraihem和Baz利用动态放大器确定了机电模型,并研究了动态放大器对输出功率的影响,但是忽略了系统阻尼和负载电阻对系统性能的影响[10]。
本文在原有单自由度压电振动能量采集器模型基础上增加一个弹性放大器,形成具有双自由度 (Two-degrees-of-freedom,简称TDOF)的压电振动能量采集器(简称PVEH),达到提高能量采集器的输出功率和拓宽工作频带的目的。为了能够清楚地解析双自由度压电能量采集器的各参数对其输出性能的影响,指导其输出性能的精确预测及优化设计,本文利用有限元方法,综合考虑采集器本体结构与负载电路间、电极与压电陶瓷间以及采集器本体结构与弹簧间的相互耦合作用,建立了带有弹簧放大器的双自由度高效压电悬臂梁振动能量采集器的有限元机电模型,并利用ANSYS有限元软件研究了系统参数(如质量比、阻尼比以及负载电阻等)对振动特性以及电输出特性的影响。
1 TDOF压电振动能量采集器的构造及其建模
1.1 TDOF压电振动能量采集器的构造
图1是TDOF压电悬臂梁振动能量采集器的结构示意图。

图1 TDOF压电悬臂梁振动能量采集器
整个能量采集器由末端带有集中质量Mt的SDOF压电双晶片悬臂梁系统和一个弹簧-质量-阻尼构成的弹性放大器系统(Elastic amplifier system, 简称EAS) 组成。压电悬臂梁系统由金属基板、双压电晶片、末端集中质量Mt和负载电路组成。双压电晶片PZT1,PZT2通过环氧树脂黏结到金属基板的上、下表面,它们沿厚度方向极化,且极化方向相反(如图1“↓”、“↑”所示),并通过串联形式连接于外加负载电阻RL(注:该电阻为能量采集器电输出端连接的AC-DC电路、滤波电路和电阻R等电路的等效阻抗,负载电阻RL的改变反映了电输出端的等效阻抗的变化)。弹性放大器系统是由质量、刚度和阻尼系数分别为Mb,Kb和Cb的弹簧质量阻尼系统组成。压电双晶片悬臂梁的左端固定在弹性放大器的质量块Mb上,弹性放大器安装在基础上。y为基础振动位移,i为流经负载电阻RL的电流。基础产生的振动,通过弹性放大器系统放大传递到压电双晶片悬臂梁系统,使得压电双晶片悬臂梁系统的弯曲振动位移被放大,达到提高系统输出能力的目的。
1.2 TDOF压电振动能量采集器的建模
TDOF压电振动能量采集器的结构模型中压电晶体与金属基体满足本构关系:
Ts=csS,
(1)
式中T为应力矢量;S为应变矢量;E为电场矢量;D为电位移矢量;cs为金属基体的刚度矩阵;cE为恒定场下压电晶体的刚度矩阵;e为压电常数矩阵;εS为介电常数矩阵;下标s和p分别代表金属材料和压电材料。
利用Hamilton原理和拉格朗日方程推导得到TDOF压电系统的机电耦合动力方程[11]
(2)
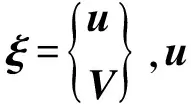
利用ANSYS有限元软件建立TDOF压电振动能量采集器的有限元模型,表1是压电振动能量采集器的结构参数,其中压电陶瓷PZT压电材料特性参数如下:
刚度矩阵(×1010N/m2)

介电常数矩阵
压电应力常数矩阵(C/m2)

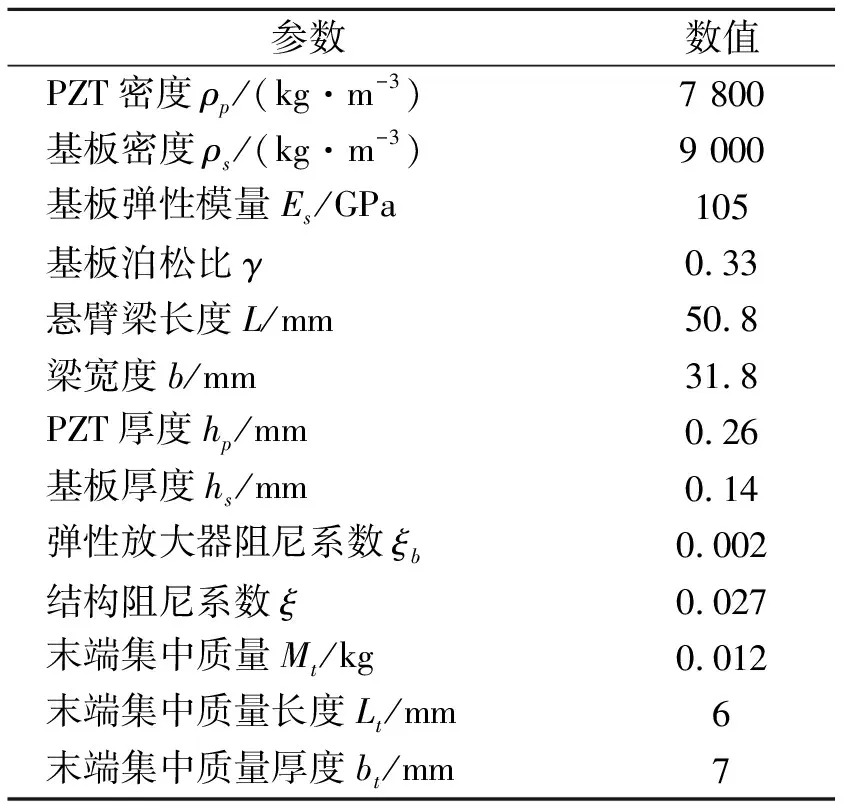
表1 TDOF压电振动能量采集器的结构参数
TDOF压电振动能量采集器的有限元模型建立步骤如下:
(1) 通过命令流的形式建立压电振动能量采集器的几何模型;
(2) 对该几何模型定义单元类型与材料属性;
(3) 运用在体上生成体单元和体扫描的方法划分网格,并进行机电耦合处理和约束处理,最终生成有限元模型。
图2为TDOF压电振动能量采集器的有限元模型。

图2 TDOF压电能量采集器有限元模型
在该模型中,采用8节点六面体耦合场SOLID5 单元对压电陶瓷进行建模,采用8节点线性结构SOLID45 单元对金属基板建模。考虑到复合材料黏结层的影响,即压电陶瓷和金属基板并不是理想黏结,并且黏结层的厚度很小,仅在几十微米到几百微米之间,因此采用SHELL63薄膜单元对黏结层进行建模。质点单元MASS21用于TDOF系统的集中质量Mb的建模,弹性单元COMBIN14用于TDOF系统弹簧-阻尼元件的建模。采用CIRCU94压电电路单元对负载电阻RL单元建模,以便产生电压、电流和输出功率。极化方向是由PZT压电材料特性中压电常数矩阵决定的。PZT1和PZT2极化方向的不同主要通过改变PZT陶瓷的压电常数d31,d33和d15的符号实现的,由于PZT1和PZT2是串联连接的,因此PZT2的压电常数d31,d33和d15与PZT1的压电常数d31,d33和d15的符号相反。将图2所示有限元模型中压电电极的各个面进行节点耦合,耦合点设置为电压自由度;与金属基板相黏结的两个压电电极耦合成一个参考点,其参考电势设为0,即参考地;上层压电片电极的节点电压自由度耦合为通用节点“1”,下层压电片电极的节点电压自由度耦合为通用节点“2”,节点“1”与节点“2”之间连接负载电阻RL。
2 数值仿真分析
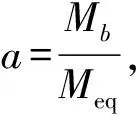
Meq=βMρAL+Mt
(3)
(4)
式中 系数βM和βK可由Rayleigh-Ritz方法推导得到;ρ,E,I,A和L分别为压电悬臂梁的等效密度、等效弹性模量、等效转动惯量、截面面积和长度。
首先对模型添加约束条件和施加外力载荷,然后再对TDOF压电振动能量采集器有限元模型进行仿真分析。先利用有限元仿真软件ANSYS对所建立的有限元模型进行模态分析。通过命令流来设置电压差以控制图2中节点“1”和节点“2”之间的电路状态,分别进行求解,并计算出相应的1阶振动模态和谐振频率。本文主要关注的是TDOF压电振动能量采集器系统1阶振型,因此,当节点“1”与节点“2”之间的电压差为0时,即负载电阻处于短路(RL→0)状态,此时模态频率为42.74 Hz,如图3所示;当节点“1”与节点“2”之间的电压差为∞时,负载电阻处于开路(RL→∞)状态,此时模态频率为44.52 Hz,如图4所示。
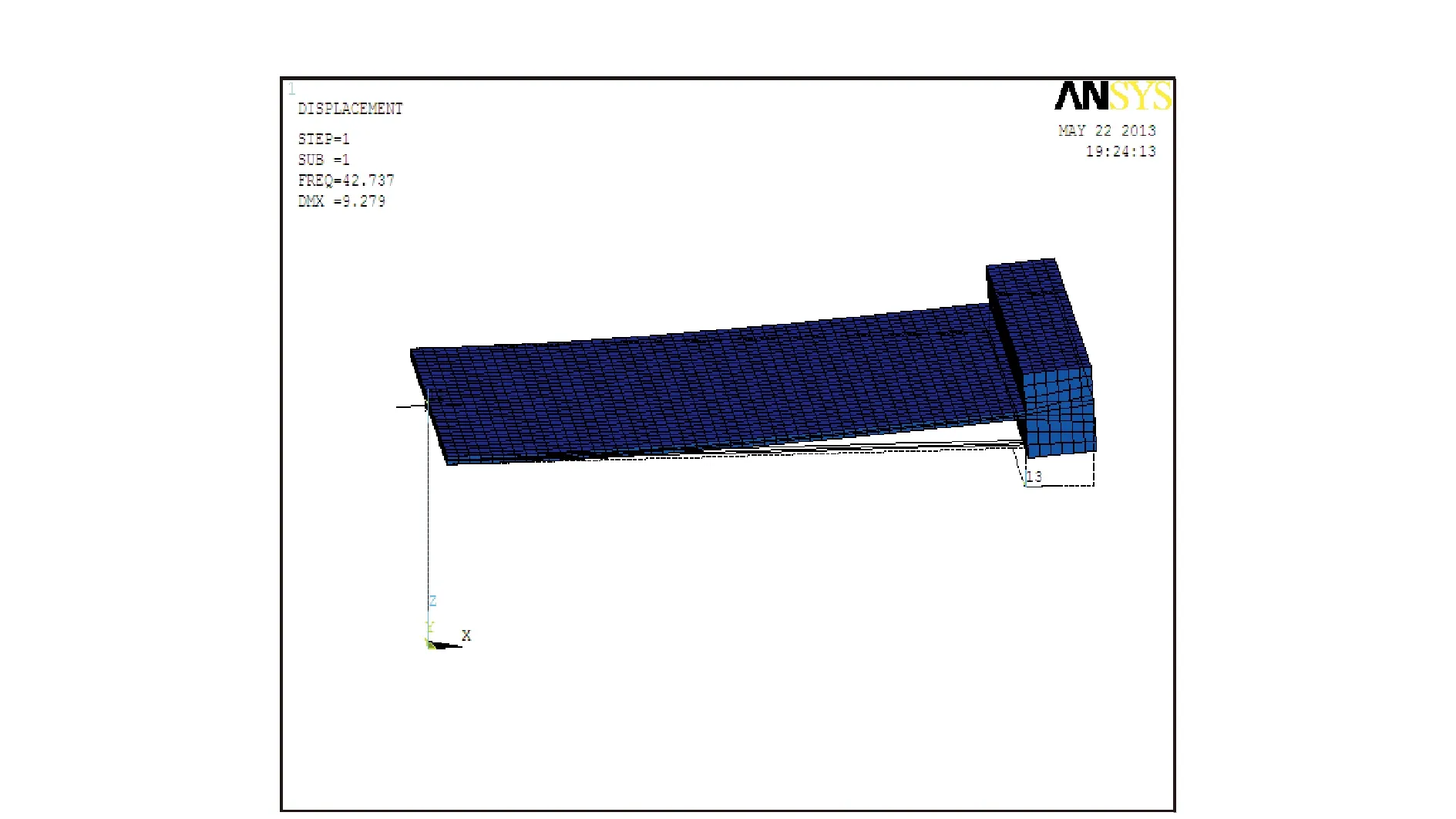
图3 TDOF压电振动能量采集器负载短路振动模态

图4 TDOF压电振动能量采集器负载开路振动模态
当基础振动角频率ω分别与弹性放大器的固有角频率ωb及悬臂梁固有角频率ωeq一致时,可以推导可知刚度比与质量比相等,整个TDOF系统达到谐振状态,压电悬臂梁的振动位移也达到最大。
图5为当负载电阻RL=1 kΩ、基础振动加速度为40 m/s2(注:下文未特别说明,基础振动加速度均为40 m/s2)时,不同质量比a下的悬臂梁末端速度v和放大器加速度G随激振频率f的变化情况。
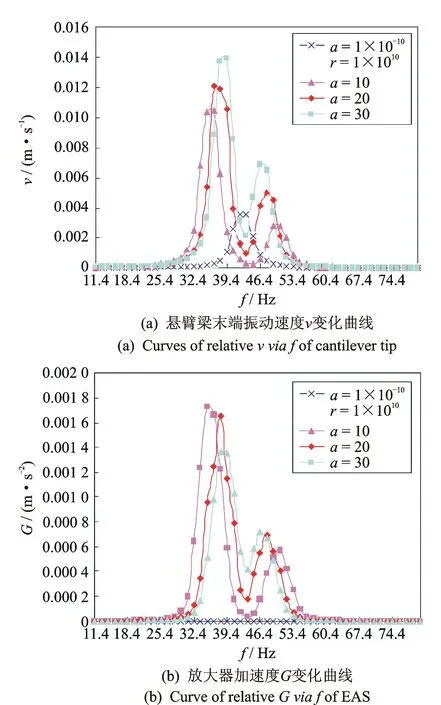
图5 不同质量比a下的悬臂梁末端速度v与放大器加速度G变化曲线
从图5(a)中可以看出,不同的质量比a下,每条悬臂梁末端振动速度随频率的变化曲线都有两个峰值,峰值点的横轴位置、纵轴大小以及两峰值间的间距都受到质量比的影响。随着质量比a的增大,峰值点的纵轴大小增大,两峰值点间的间距变窄,逐渐形成一个宽频带窗口,这有利于拓宽压电采集器的工作频带。特别指出,在质量比a=1×10-10(即a→0)和刚度比r=1×1010(即r→∞)下,TDOF压电能量采集器缩减成SDOF悬臂梁发电系统,其末端振动速度如图5(a)中a=1×10-10,r=1×1010曲线所示。另外,在某个质量比a下,会使得末端振动速度的谷值等于SDOF系统末端振动速度的最大值。由此说明,SDOF系统加入弹性放大器后,不仅拓宽了整个系统的工作频带,还提高了末端振动速度。从图5(b)可以看出,不同的质量比a下,每条放大器相对加速度曲线都有两个峰值,随着质量比a的增加,左峰点的幅值减小,这表明部分弹性放大器的机械能转换成了悬臂梁的振动能量;右峰点的幅值随质量比a增大,这表明部分压电悬臂梁的机械能转换成了弹性放大器的振动能量;另外,左右峰值间距变窄,逐渐形成一个宽频带窗口。特别指出,在质量比a=1×10-10(即a→0)和刚度比r=1×1010(即r→∞)下,弹性放大器变成刚性,没有起到放大作用。由图5分析可知,合适的质量比,不仅可以提高末端振动速度,还可以拓宽频率工作带。
图6为当负载电阻RL=1 kΩ时不同质量比a下的负载输出电压U与负载输出功率P随频率f的变化情况。图中为了便于观察,纵坐标采用了对数形式。
由图6可知,负载输出电压变化曲线和负载输出功率变化曲线的变化趋势与图5(a)末端振动速度曲线趋势相同。在质量比a=20时,负载电压和功率输出曲线的谷值等于SDOF系统的最大值。另外,随着质量比a的增大, 负载的输出电压和功率也随之增大。

图6 不同质量比a下的输出电压U与输出功率P变化曲线
图7是当质量比a=20和负载电阻RL=1 kΩ时,不同阻尼比c对TDOF系统输出功率P的影响仿真曲线。由图7可知,随着阻尼比c的增大,TDOF系统的输出功率左右峰值逐渐减小,当弹性放大器的阻尼系数增大到远超于悬臂梁系统的阻尼系数时,弹性放大器的放大作用就会失去,TDOF系统输出功率的左右峰值就会合并为一个峰值。这说明小的阻尼比c能够使输出功率有所提高。
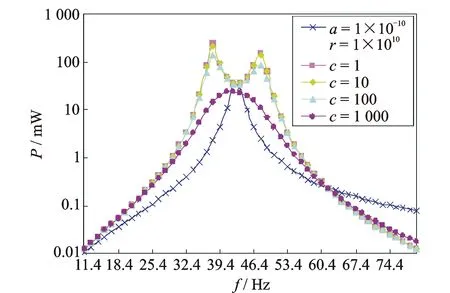
图7 不同阻尼比c下的输出功率P变化曲线
3 负载输出功率优化
在SDOF压电振动能量采集系统中引入弹簧放大器后,使得振动特性和电输出特性有明显的改善。对于给定的激励条件下,负载电阻与TDOF压电振动系统的阻抗匹配时,能够使TDOF压电振动系统输出最大功率。因此,对负载输出功率最大化进一步仿真分析与研究。
图8是TDOF压电振动能量采集器系统输出功率P随负载电阻RL的变化关系。由图8可知,当系统的负载电阻RL趋于0时,即TDOF系统处于短路状态,最佳匹配负载电阻为Rsc=42.3 kΩ,此时,系统负载输出功率最大;当系统的负载电阻RL趋于∞时,即TDOF系统处于开路状态,最佳匹配负载电阻为Roc=90.8 kΩ,此时系统负载输出功率最大。
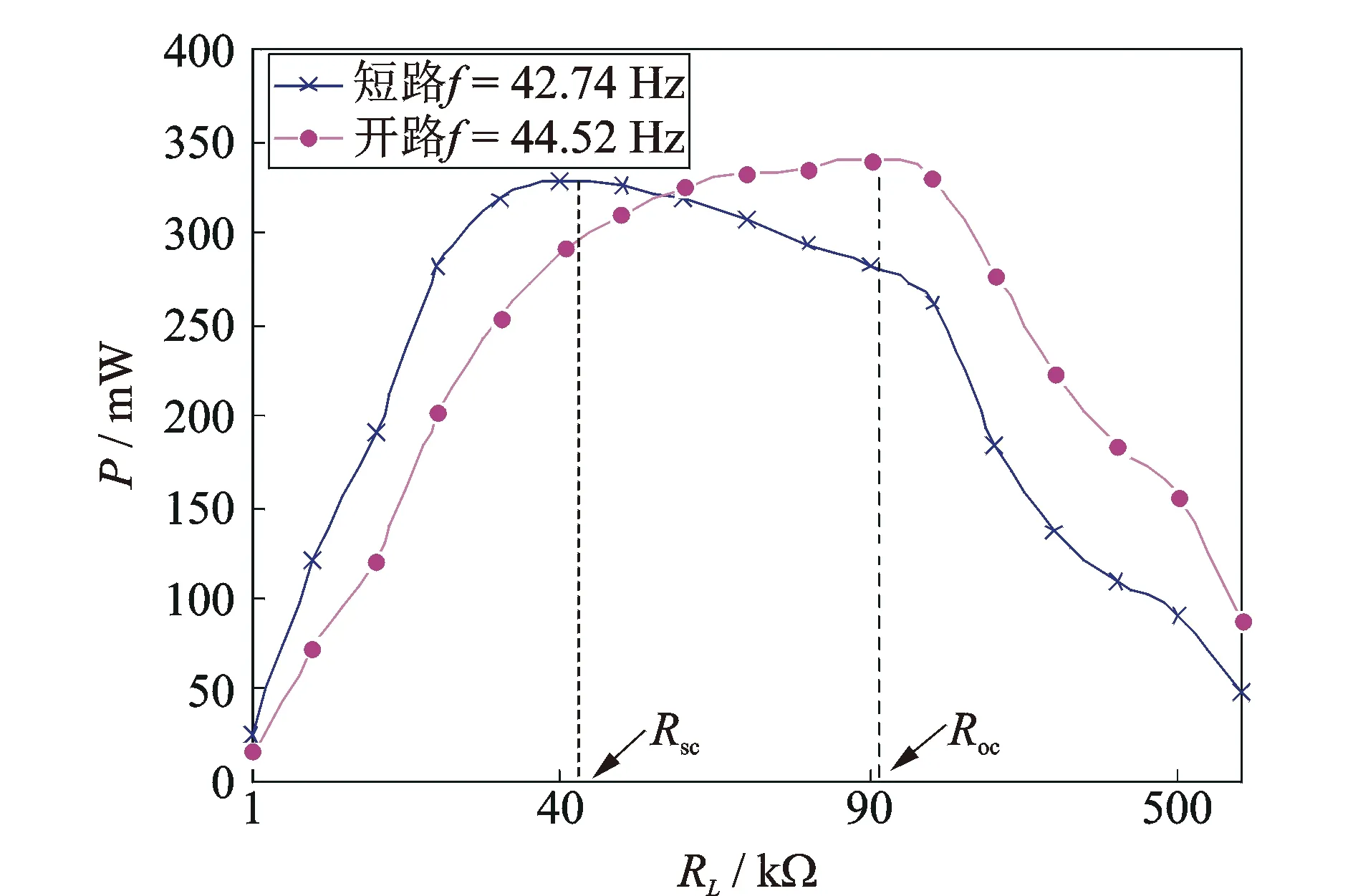
图8 不同电阻下的输出功率P变化曲线
图9是当质量比a=20时,最佳匹配电阻对TDOF压电振动系统的电输出特性(输出电压U、输出电流I和输出功率P)的影响。从图9(a),(b)和(c)中可以看出,TDOF能量采集器在负载电阻Rsc=42.3 kΩ和负载电阻Roc=90.8 kΩ下电输出曲线都有两个峰值,且每条曲线的谷值都明显地大于SDOF压电系统的相应电输出曲线的最大值。从图9(a)和(b)中得出TDOF压电系统和SDOF压电系统的共同点:负载电阻Rsc=42.3 kΩ时的输出电压小于负载电阻Roc=90.8 kΩ时的输出电压,但输出电流恰恰相反。除此之外,还可以知道图9(a)中最大的峰值电压出现在负载电阻Roc=90.8 kΩ时,而图9(b)中最大的峰值电流出现在负载电阻Rsc=42.3 kΩ时。这说明,TDOF系统处于反谐振状态下,能够输出较大的工作电压;处于谐振状态下,能够输出较大的工作电流。

图9 不同负载电阻下电输出的变化曲线
根据结合图9(c)得到最佳匹配电阻下的TDOF和SDOF的对比表,结果如表2所示。表2中f代表相应匹配电阻下的谐振频率,P代表相应匹配电阻下的输出功率,fB代表系统的工作频率带宽。
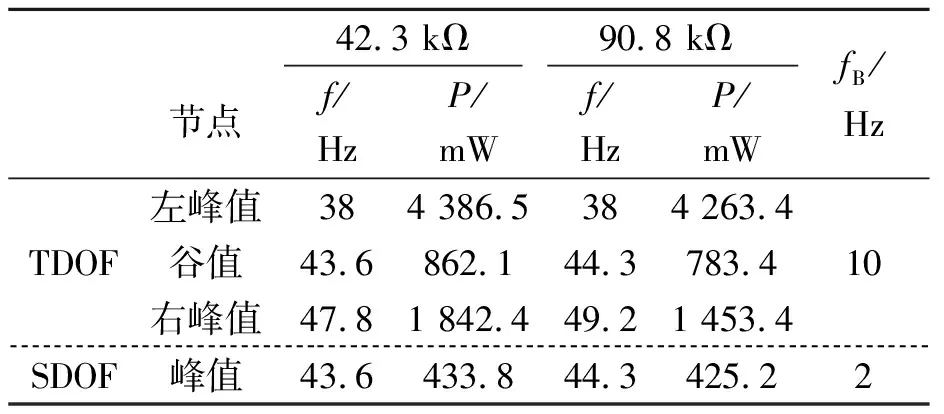
表2 最佳匹配电阻下的TDOF和SDOF对比
从表中看出,系统在短路最佳匹配电阻和开路最佳匹配电阻条件下,TDOF系统的左峰值输出功率约是SDOF系统输出功率的10倍;TDOF系统左右峰值间的最小输出功率(即谷值输出功率)是SDOF系统的2倍。并且TDOF系统的工作频率带宽也是SDOF的5倍。
将图9(c)与Wang等所作的单自由弹性体系压电悬臂梁能量采集器的研究结果(如图10所示)进行了比较[13]。虽然两者压电晶体的材料特性不一样,导致两者短路状态和开路状态下的谐振频率不一样。但是,两者的电输出特性和振动特性随频率的变化趋势和输出功率随负载电阻的变化趋势是相同的,这间接验证了本文有限元模型仿真结果的有效性。
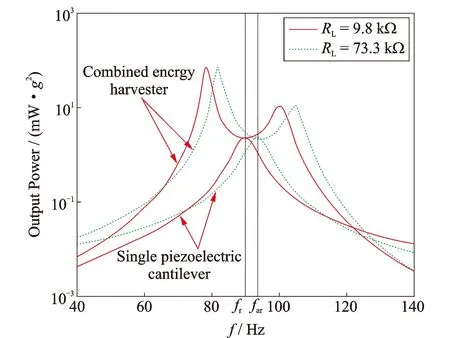
图10 文献[13]模型不同负载下的输出功率
4 结 论
本文通过有限元软件ANSYS对TDOF压电振动能量采集器建立有限元模型和研究,利用有限元分析方法研究了系统参数(如质量比、阻尼比以及负载电阻等)对振动特性以及电输出特性的影响。综合所得出的曲线关系图,得出以下结论:
(1) 弹性放大器不仅提高了末端振动速度,还可以拓宽频率工作带和提高输出功率。在基础振动加速度为40 m/s2条件下,系统短路谐振和开路谐振最大输出功率分别达到4 386.5和4 263.4 mW,是SDOF系统输出功率的10倍。TDOF系统工作频带宽度达到10 Hz,是SDOF系统的5倍。
(2) 大质量比a和小阻尼比c可以拓宽工作频带和输出较大的功率。
(3) 反谐振状态下的匹配电阻能够使TDOF系统输出较大的工作电压;而谐振状态下的匹配电阻能够使TDOF系统输出较大的工作电流。
参考文献:
[1] Raghunathan V, Kansal A, Hsu J, et al, Design considerations for solar energy harvesting wireless embedded systems[A]. IEEE International Symp. on Information[C]. 2005.
[2] Mathuna C O, Martinez-Catalar V, O’Donnel T, et al. Energy scavenging for long-term deployable wireless sensor networks [J]. Talanta,2008, 75(3):613—623.
[3] Sari I, Balkan T, Kulah H, An electromagnetic micro power generator for low-frequency environmental vibrations based on the frequency upconversion technique [J]. Journal of Microelectromechanical Systems, 2010, 19 (1):14—27.
[4] Hoffmann D, Folkmer B, Manoliy Y, Fabrication, characterization and modeling of electrostatic micro-generators [J]. Journal of Micromechanics and Microengineering, 2009, 19:094001—094012.
[5] Kim M, Hoegen M, Du Gundj I J, Modeling and experimental verification of proof mass effects on vibration energy harvester performance[J]. Smart Materials and Structures, 2010, 19(4):045023—045043.
[6] Liao Y B, Sodano H A, Model of a single mode energy harvester and properties for optimal power generation[J], Smart Materials and Structures, 2008, 17(6):065026—065040.
[7] Challa V R, Prasad M G, Shi Y, et al. A vibration energy harvesting device with bidirectional resonance frequency tenability[J]. Smart Materials and Structures, 2008, 17(1):015035—015046.
[8] Wu W, Chen Y, Lee B, et al. Tunable resonant frequency power harvesting devices[A]. Proceedings of SPIE-The International Society for Optical Engineering[C]. 2006, 6169:61690A.
[9] Ma P S, Kim J E, Kim Y Y, Power amplifying strategy in vibration powered energy harvesters[A]. Proceedings of SPIE-The International Society for Optical Engineering[C]. 2010, 7643:76430O.
[10] Aldraihem O, Baz A, Energy harvester with dynamic magnifier[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(6):512—530.
[11] HAGOOD N W, CHUNG W, VON FLOTOW A. Modeling of piezoelectric actuator dynamics for active structural control[J]. Journal of Intelligent Material Systems and Structures, 1990, 1(3):327—354.
[12] 王光庆, 金文平, 展永政,等. 压电振动能量采集器的力电耦合模型及其功率优化[J]. 传感技术学报, 2013, 26(8):1 092—1 099.WANG Guangqing, JIN Wenping, ZHAN Yongzheng, et al. A force-electric coupling model and power optimization of piezoelectric vibration energy harvester[J]. Chinese Journal of Sensors and Actuators. 2013, 26(8):1 092—1 099.
[13] Wang H Y, Shan X B, XIE T. An energy harvester combining a piezoelectric cantilever and a single degree of freedom elastic system[J]. Journal of Zhejiang University-SCIENCE A, 2012, 13(7):526—537.

