基于部分集成局部特征尺度分解与拉普拉斯分值的滚动轴承故障诊断模型
程军圣, 郑近德, 杨 宇, 罗颂荣
(湖南大学汽车车身先进设计制造国家重点实验室, 湖南 长沙 410082)
引 言
滚动轴承的故障诊断过程可分为三个步骤:信号采集、特征提取和状态识别[1]。 由于滚动轴承振动信号大部分是非线性、非平稳信号,因此其故障诊断的关键是如何从非线性、非平稳信号中提取故障特征信息[2]。 由HUANG等提出的经验模态分解(Empirical mode decomposition,EMD)自适应地将一个非平稳信号分解为若干个瞬时频率具有物理意义的内禀模态函数(Intrinsic mode function,简称IMF)之和[3,4],能有效地提取信号的本质特征,在机械故障诊断领域得到了广泛的应用。如,程军圣等提出了一种基于EMD的能量算子解调方法,并将其应用于滚动轴承故障诊断[5];雷亚国等提出了一种基于EMD的滚动轴承混合智能故障诊断模型等[6];由于EMD存在模态混淆问题,HUANG等提出了一种基于噪声辅助分析的总体平均EMD方法(Ensemble EMD,EEMD),基于此,周智等提出了一种基于EEMD和共振解调的滚动轴承自适应故障诊断方法[7];雷亚国等在文献[8]中综述了近年来EMD和EEMD在机械故障诊断中的应用。
作为对EMD方法的改进,文献[9]提出了另一种自适应信号分解方法—局部特征尺度分解(Local characteristic-scale decomposition,LCD),LCD采用新的方法定义均值曲线,自适应地将一个非平稳信号分解为若干个内禀尺度分量(Intrinsic scale component,ISC)和一个趋势项之和,与EMD相比,LCD减小了拟合误差,提高了计算速度,且对模式混淆也有一定的抑制,LCD已经被应用于机械设备故障诊断[10]。 然而与EMD方法类似,LCD也存在模态混淆。 最近,笔者提出了一种抑制LCD模态混淆的方法——部分集成局部特征尺度分解[11]。 PELCD向待分解信号成对地添加符号相反的白噪声,对加噪信号依据频率高低逐层进行集成平均分解,在检测出引起模态混淆的高频间歇和噪声信号后,将其从原始信号中分离,再对得到的剩余信号进行完整LCD分解。PELCD方法不但能够在一定程度上抑制模态混淆,而且克服了集成平均方法的计算量大、分量未必满足ISC定义条件等缺陷,具有一定的优越性。不足的是,PELCD参数的选择具有主观性,论文对其进行了研究和改进,减小了参数的选择对分解结果的影响,并将改进后的PELCD方法应用于滚动轴承振动信号的预处理,将振动信号分解为若干个ISC分量之和, 再提取振动信号时频域特征——时频熵和前几个ISC分量的时域和频域统计特征以及复杂度等特征。
提取上述滚动轴承故障特征信息之后,为了避免特征向量维数过高而引起信息冗余,降低诊断的效率,论文采用拉普拉斯分值对特征量按照重要程度进行排序[12,13],从中选择与故障关系最为密切的特征值作为特征向量表征故障特征,从而降低了特征向量的维数,提高了诊断的速度和效率。
同时,为了减少对人为经验的依赖,实现滚动轴承故障的自动诊断,需要选择合适的决策方法。常用的模式识别方法,如人工神经网络(BP神经网络和RBF神经网络等)[14,15],支持向量机(Support vector machine,SVM)等已广泛应用于机械设备故障诊断[16,17]。但是神经网络结构和类型的选择过分依赖先验知识,分类精度受初始条件的影响;SVM需要事先选择核函数及其参数,且其本质上是二分类,对多分类问题则需要进行多次二分类。最近,Raghuraj等人提出了一种基于变量预测模型的模式分类方法(VPMCD)[18,19],VPMCD基于假设特征值之间存在内在关系建立数学模型,针对不同的类别获得不同的数学模型,采用数学模型对特征值进行预测,把预测结果作为分类的依据,进一步进行分类识别。VPMCD无需事先选择参数,避免了神经网络的迭代和SVM的寻优过程,减少了计算量,是一种有效的模式分类方法。
基于上述分析,论文提出了一种基于PELCD,LS和VPMCD的滚动轴承故障诊断模型。首先,采用PELCD对滚动轴承振动信号进行分解,得到若干个ISC分量;其次,选择前几个包含主要故障信息的ISC分量,并分别提取其时域和频域故障特征参数,再提取振动信号的时频域特征值,组成初始特征向量;第三,采用拉普拉斯分值对初始特征向量的各个特征值按照重要性进行排序,并依据分值由小到大的顺序选择前若干个较重要的特征值作为特征向量;最后,将特征向量输入VPMCD分类器实现滚动轴承故障类型和程度的自动诊断。实验数据分析结果验证了该模型的有效性。
1 部分集成局部特征尺度分解方法
1.1 算法过程
虽然与EMD相比,LCD减小了拟合误差,提高了计算速度,有一定的优越性。 但与EMD类似,LCD也存在模态混淆。 针对此,文献[11]提出了一种基于噪声辅助的部分集成局部特征尺度分解方法(PELCD),步骤如下:
1)假设待分解信号为S(t),添加符号相反的白噪声到S(t),即
(1a)
(1b)
式中ni(t)表示添加的白噪声,a表示添加白噪声幅值,i=1,2,…,Ne,Ne表示添加白噪声对数。
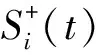
(2)
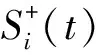
(3)
4.再对剩余信号r(t)进行完整LCD分解。
其中,文献[11]中第(3)步高频间歇或噪声的检测方法为基于排列熵的随机性检测[20,21],通过设置排列熵阈值(原文献设为0.6)来实现分解的自适应性;但是排列熵阈值的选择较具有主观性,且添加白噪声幅值和数目也依据主观选择,论文对PELCD方法进行了如下方式的改进:
1)向待分解信号S(t)添加一对幅值为ak但符号相反的白噪声,其中ak=0.05kSD,k=1,2,…,8;SD为原始信号的标准差,集成次数Ne固定为100(即添加白噪声对数为50);
2)对加噪信号执行完整LCD分解再集成平均,依据分解正交性指标(index of orthogonality,IO)最小和得到的分量个数最少选择最优分解结果[3];
3)i=1,计算最优分解每一阶ISC分量Ii(t)排列熵值PEi;
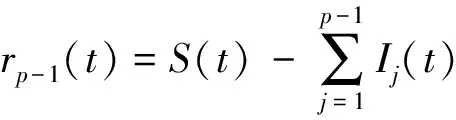
(II)若0.6≥PEp≥0.4,则分别对剩余信号rp-1(t)和rp(t)进行完整LCD分解,再依据IO最小选择分解结果;
(III)若0.6≥PEp-1>PEp≥0.4,则对剩余信号rp-2(t),rp-1(t)和rp(t)分别进行完整LCD分解,再依据分量正交性最小选择分解结果;以此类推。
PELCD由于成对地添加白噪声,减小了噪声残留,保证了分解的完备性;同时通过及时检测间歇或噪声等引起分解模态混淆的高频信号,避免了不必要的集成平均,不但能够抑制模态混淆,而且使得更多分量满足ISC判据条件。
1.2 仿真分析
为了说明PELCD的有效性,首先考虑如图1所示的仿真信号x=x1+x2,其中x1=cos2π10t,x2是由两段频率为100 Hz幅值为0.1的正弦信号构成的间歇信号。
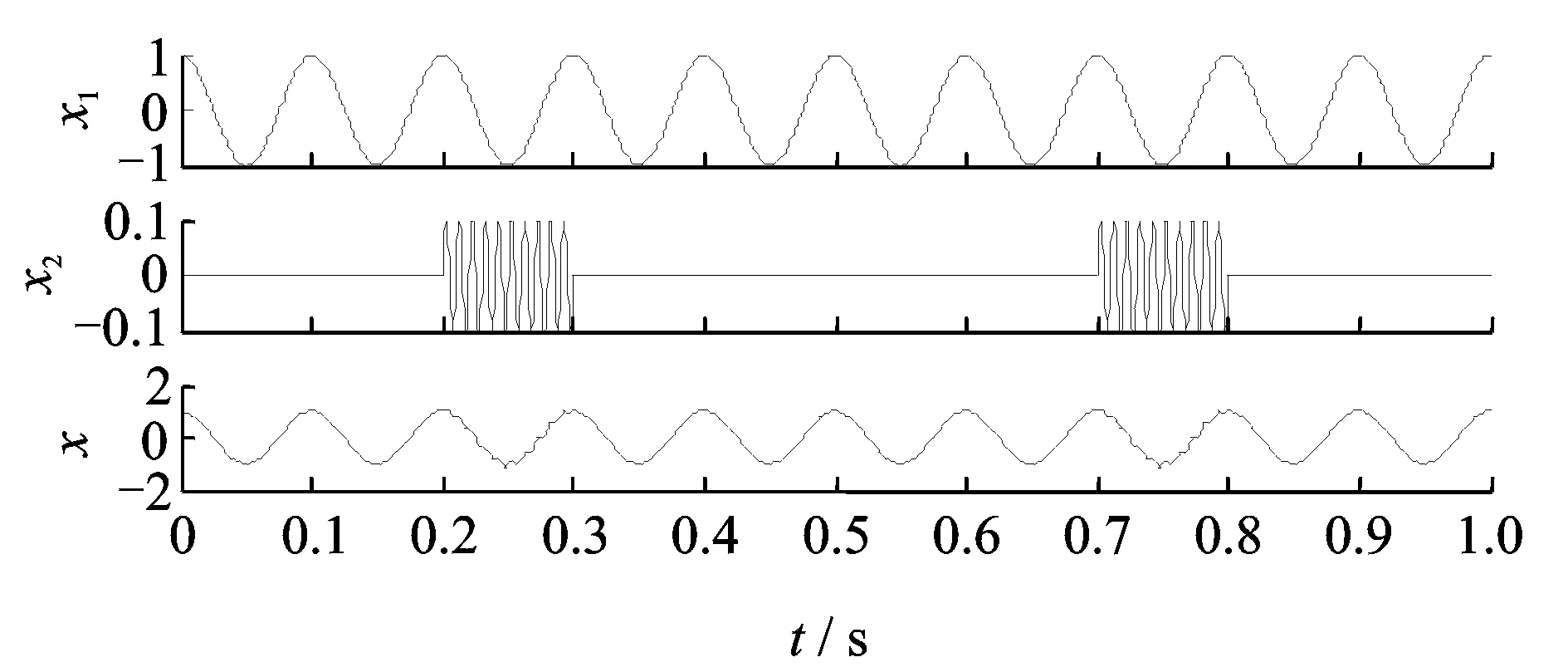
图1 仿真信号x及各成分的时域波形
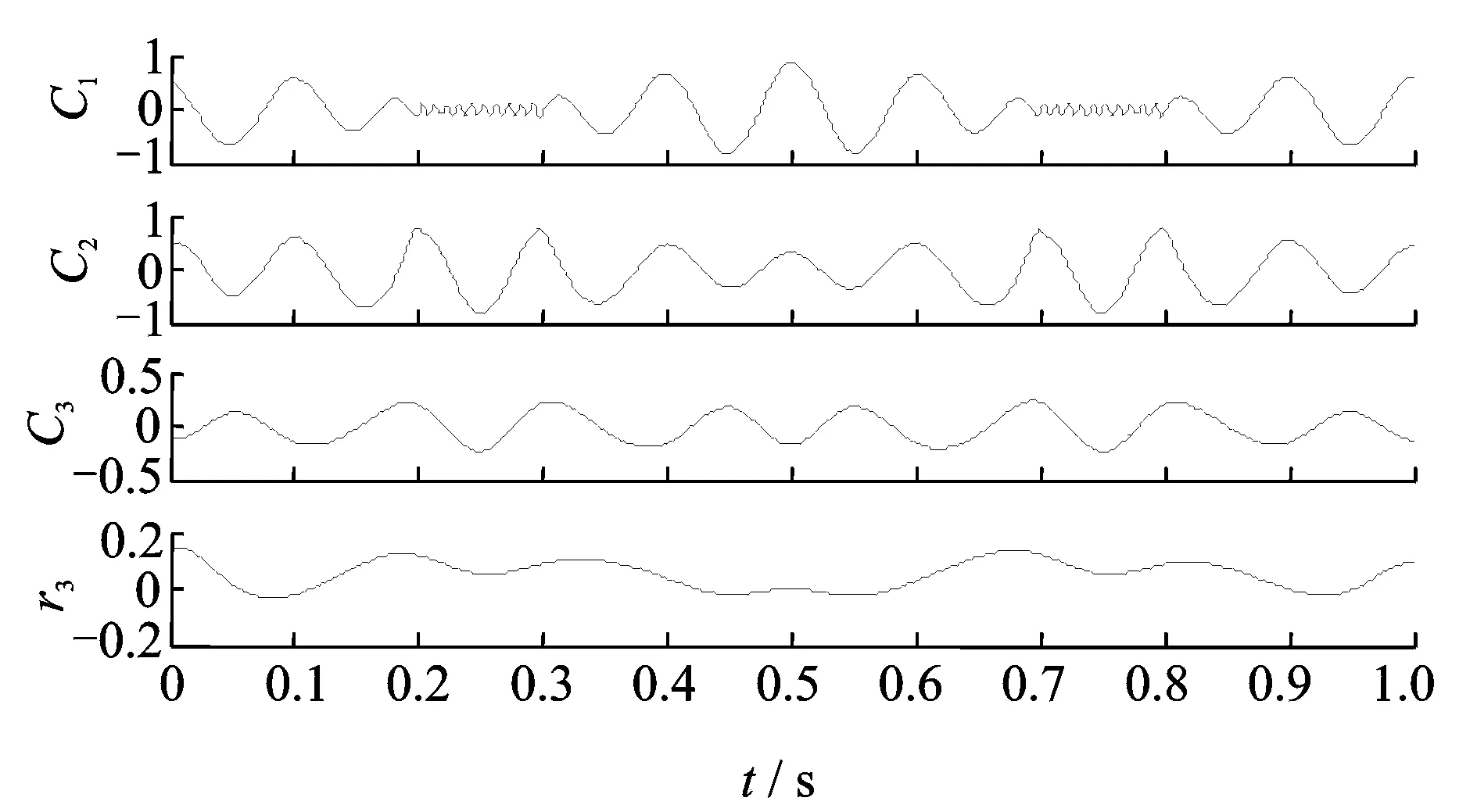
图2 仿真信号x的LCD分解结果
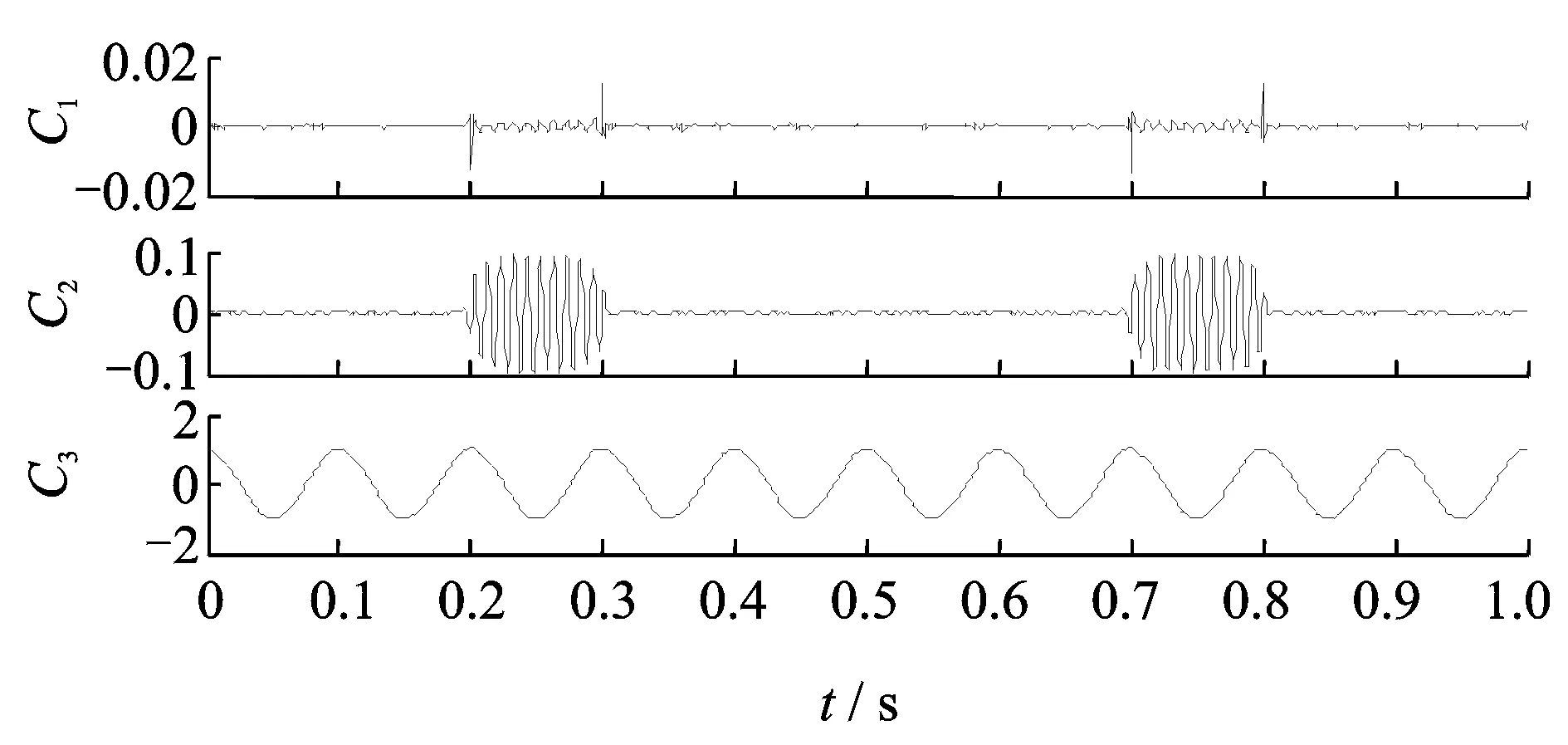
图3 仿真信号x的PELCD分解结果
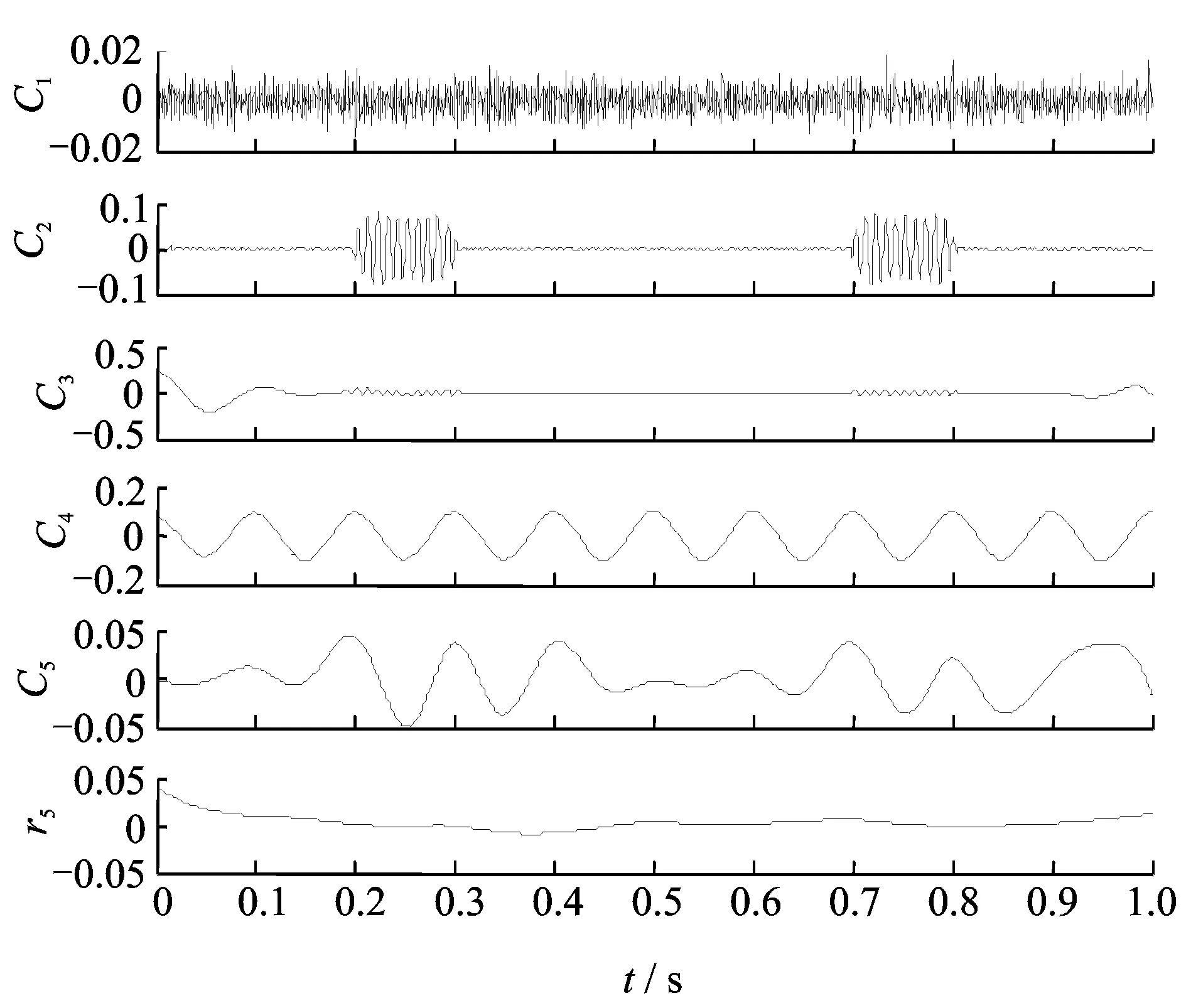
图4 仿真信号x的EEMD分解结果
首先分别采用LCD和PELCD对其进行分解,结果分别如图2和3所示,图中Ci表示第i个ISC分量,ri表示剩余项。由图2可以看出,LCD分解结果出现了严重的模态混淆,得到的ISC分量失去了物理意义。而由图3,PELCD则能够有效和准确地将余弦信号从高频间歇中分离出来,C3对应真实分量x1。为说明PELCD抑制模态混淆的能力,采用公认的抑制分解模态混淆效果较好的EEMD对上述信号进行分解[9],分解结果如图4所示。从图4中可以看出,虽然EEMD也能够将余弦信号从高频间歇信号中分离出来,但是分解出现了虚假分量C3和C5,其中C5和C4具有相同的频率。因此比较而言,PELCD分解结果是最优的。
调制与冲击是机械发生故障的两种典型形式[22]。构造图5所示故障模拟信号,其中x1(t)为背景干扰噪声,x2(t)为故障高频冲击信号,x3(t)为表示恒定转速正弦信号,x4(t)为调制信号,x5(t)为趋势项,x(t)为前5者的混合信号。采用PELCD对混合信号x(t)进行分解,结果如图6所示。由图6可以看出,PELCD分解得到的分量I1(t),I2(t),I3(t),I4(t)和趋势项R4(t)分别对应为x1(t),x2(t),x3(t),x4(t)和趋势项x5(t),除了第一个背景噪声分量外,其他分量与真实信号的相关性系数分别为0.976 7,0.993 9,0.986 9和0.998 7。这说明PELCD能够从混合信号中精确地提取出冲击、转速和调制成分,因此,PELCD适合处理滚动轴承振动信号。
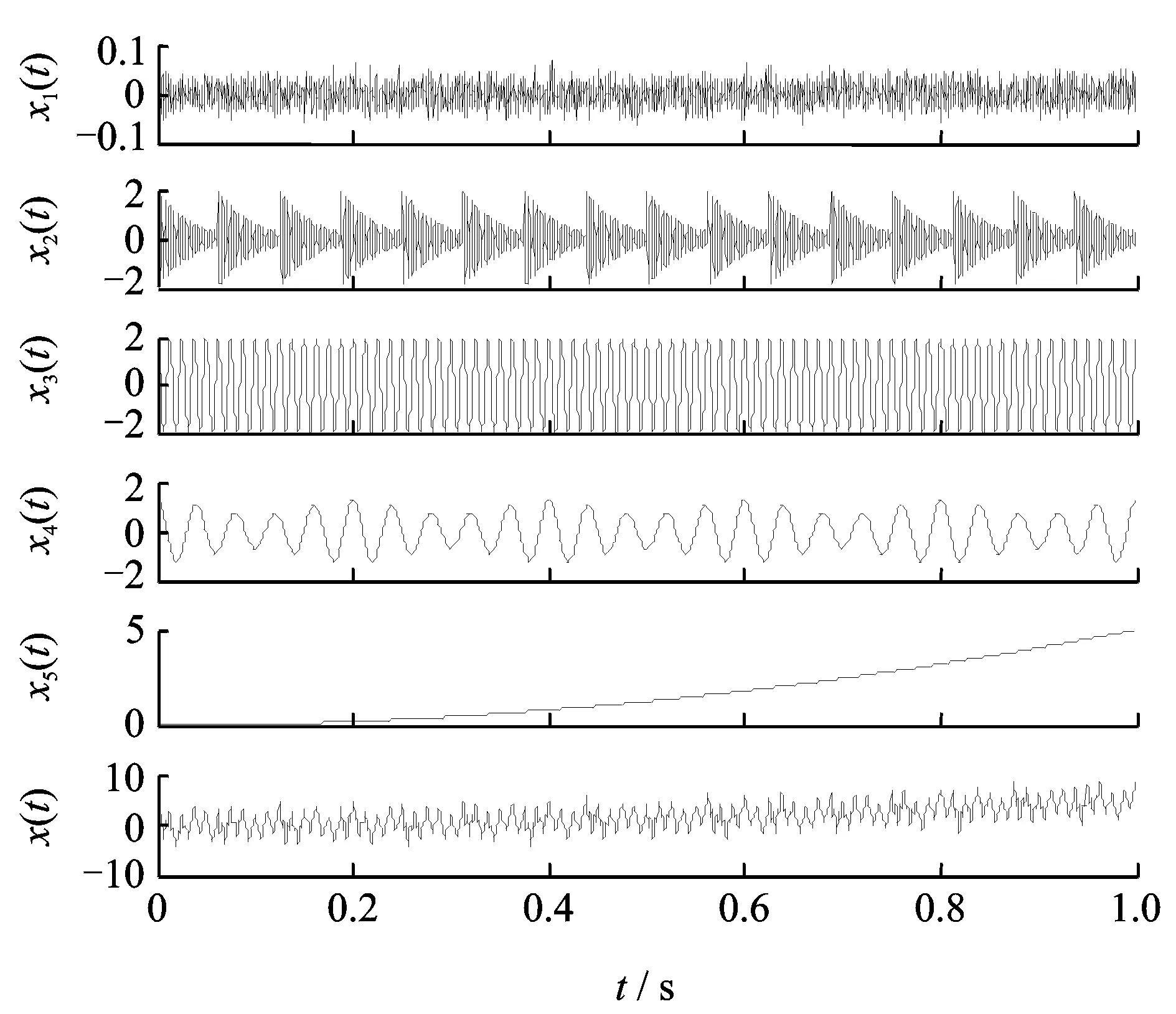
图5 故障模拟信号及各成分时域波形
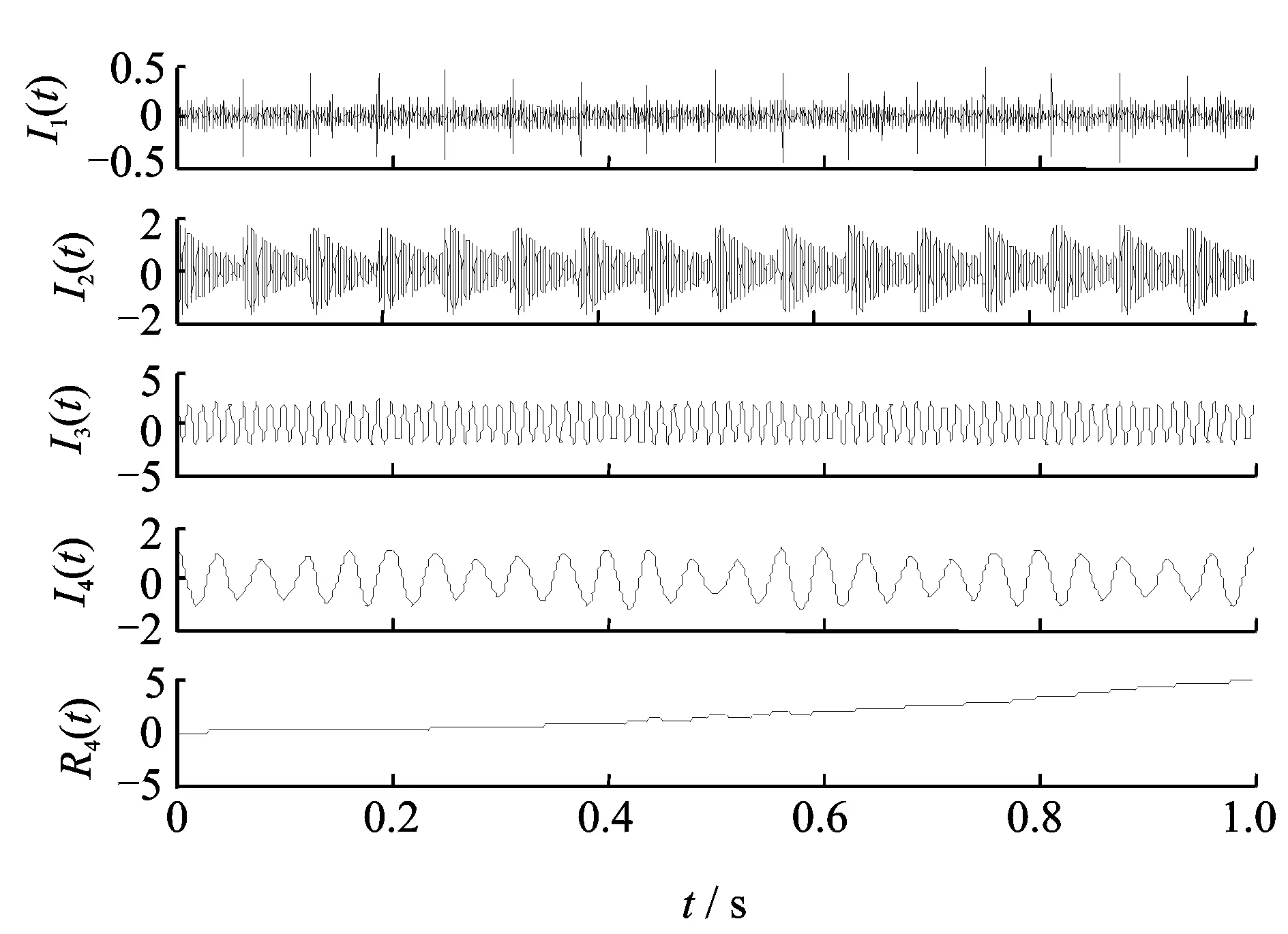
图6 图5所示故障模拟信号PELCD分解结果
2 特征量的提取、选择与识别
2.1 特征量的提取
由于不同故障的振动信号的特征不同,并非分解得到的所有分量都对故障诊断有贡献,故障特征分量只集中在某一个或特定的几个分量,而其他的分量对故障的诊断贡献不大,将其作为特征参数势必会造成信息的冗余;不仅如此,由于滚动轴承振动信号特征的复杂性,基于单一时域或频域的特征提取方法有一定的局限性,需要同时提取振动信号的时域和频域特征。雷亚国等在文献[22]中同时提取IMF分量的时域和频域特征:标准差、峭度、形状指标、冲击指标和频率标准差等,具有很好的诊断效果。然而,提取特征因子过多,导致特征向量维数较高,影响故障诊断的速度和效率。
论文选择如下特征值,时域:峭度(KS)、波形指标(SF)、冲击指标(IF)、模糊熵(FE);频域:重心频率(FG)、频率标准差(FSTD)、频率均方根(FRMS)、时频域:时频熵(TFE)。
对上述特征值的物理意义作如下说明:
(1)时域特征(如:峭度、波形指标、冲击指标)和频域特征(如:重心频率、频率标准差、频率均方根)等是基于统计学特征的物理量[22],反映了振动信号时域和频域的幅值和能量以及波动情况的变化,当振动信号发生变化时,这些特征能够从时域和频域同时准确地监测到,因此,它们能够有效地表征故障数据的特征。
(2)模糊熵与样本熵类似[23],是一种衡量时间序列复杂性程度的参数,属于非线性科学和信息论的范畴。序列越复杂,自相似性越低,熵值越大,序列越规则,自相似性越高,熵值越小。但与样本熵不同,模糊熵中的相似性度量函数采用模糊函数取代样本熵中的阶跃函数,使得熵值随参数的不同而变化较平缓。模糊熵已经成功地应用于滚动轴承故障特征的提取,其详细定义参见文献[23,24]。
综上,论文提取振动信号分解分量具有物理意义的时域、频域统计特征和复杂度以及振动信号的时频熵,从时域和频域以及时频联合域监测振动信号能量、幅值和复杂度的变化,较早和准确地从多个角度反映振动信号故障变化特征。
2.2 基于拉普拉斯分值的特征选择
以上提取的故障特征,虽然能够从不同的角度来反映故障程度和类型,但是它们对于不同的故障具有不同的敏感程度,一部分特征与故障密切相关,另一部分则是无关或者冗余的特征;如果将上述提取的全部特征值作为特征值,则特征向量维数过高,造成信息的冗余和分类耗时;因此,在特征向量集输入分类器之前,如果能够将上述特征量,按照与故障密切相关程度从高到低进行排序,再采用与故障特征相关程度较高的特征量进行训练和测试,不但可以提高分类的性能、避免维数灾难,而且更能够提高故障诊断的速度和效率。
拉普拉斯分值是以拉普拉斯特征值映射和局部保持投影为基础[12,13],将复杂的高维特征空间转化为简单的低维特征空间的方法,其基本思想是通过局部保持能力来评估特征值。通过直接对特征集进行学习,提取数据内在的信息结构,在特征空间中选取分值较小的特征。LS可以极大地保留故障信号特征集合中内含的整体几何结构信息,从而更有利于故障判别与诊断。
基于LS的特征选择步骤如下[12]:
令Lr为第r个特征值的拉普拉斯分值,fri为第i个样本的第r个特征值(i=1,2,…,m)。
(1)用m个样本点构建一个近邻图G,第i个节点对应xi。如果xi与xj足够“近”,比如,xi是xj的k近邻节点或者xj是xi的k近邻节点(本文中k=5),则有边连接,否则没有边连接。当节点的标号已知时,可以在同一标号的两节点之间连接一条边;
(2)如果节点i与节点j是连通的,则令
Sij=exp(-‖xi-xj‖2/t)
(4)
式中t是一个合适的常数;否则,令Sij=0。
加权矩阵S称为图G的相似矩阵,用来衡量近邻样本点之间的相似性,描述了数据空间的固有局部几何结构。
(3)对于第r个特征,定义
fr=[fr1,fr2,…,frm]T,D=diag(SI),
I=[1,…,1]T,L=D-S
(5)
矩阵L称为图G的拉普拉斯矩阵。为了避免由于某些维度数据差异很大而主导近邻图的构造,对各个特征进行去均值化处理得到
(6)
(4)计算第r个特征值的拉普拉斯分值Lr为
(7)
式中Var(fr)为第r个特征值的方差。对于一个较好的特征值,Sij越大,(fri-frj)2越小,LS也越小,表明样本在该特征上的差异越小,即该特征的局部信息保持能力越强。计算每一个特征值的得分,并对这些特征值得分从低到高进行排序,排在越前的特征越重要。特征得分与特征重要性成反比,特征得分越低,该特征越具有特征选择的重要性。拉普拉斯分值选取Lr值最小的前若干个特征值作为最优的特征选择结果[12,13]。LS在故障诊断领域的应用尚不多,论文采用LS选择与故障特征信息最相关的特征量。
下一步需要采用合适的模式识别的方法对故障类型和故障程度进行分类,实现故障类别的自动诊断。机械故障诊断中常用的模式识别方法如人工神经网络和支持向量机等,都有其自身无法克服的缺陷。最近,Raghuraj等提出了一种基于变量预测模型的模式分类方法(VPMCD),VPMCD基于假设特征值之间存在内在关系建立数学模型,针对不同的类别获得不同的数学模型,采用数学模型对特征值进行预测,把预测结果作为分类的依据,进一步进行分类识别。VPMCD无需事先选择参数,避免了神经网络的迭代和SVM的寻优过程,减少了计算量,是一种有效的分类方法。VPMCD的详细介绍参见文献[18,19]。
3 滚动轴承故障诊断模型
3.1 模型的提出
论文提出的滚动轴承故障诊断模型主要包含以下步骤:
(1)采用PELCD对每一个滚动轴承振动信号进行分解,得到若干个ISC分量;
(2)选择前三个ISC分量,提取它们的时域和频域特征值(如2.1部分定义),以及振动信号的时频熵,由此组成初始特征向量;即:提取前三个分量I1(t),I2(t)和I3(t)的特征参数:KS,SF,IF,FE和FG,FSTD,FRMS,再提取振动信号的时频熵TFE。于是可构建特征向量:T=[TFE,KS1,SF1,IF1,KS2,SF2,IF2,KS3,SF3,IF3,FE1,FE2,FE3,FG1,FSTD1,FRMS1,FG2,FSTD2,FRMS2,FG3,FSTD3,FRMS3]。T的维数为1×22,为方便,T的各对应特征值记为Ti,i=1,2,…,22;
(3)计算由初始特征向量T组成的初始特征向量矩阵的LS得分,依据分值由低到高对特征量进行排序,选择分值较小的前若干个特征向量作为最优特征向量;
(4)将最优特征向量输入VPMCD分类器进行训练和测试,实现滚动轴承故障诊断。
3.2 实验数据分析
为了验证论文提出的滚动轴承故障诊断模型的有效性,采用滚动轴承实验数据对其进行验证。实验数据来自美国凯撒西储大学滚动轴承数据中心,实验装置描述参见文献[26]。实验数据说明如表1所示。各类信号的时域波形如图7所示。
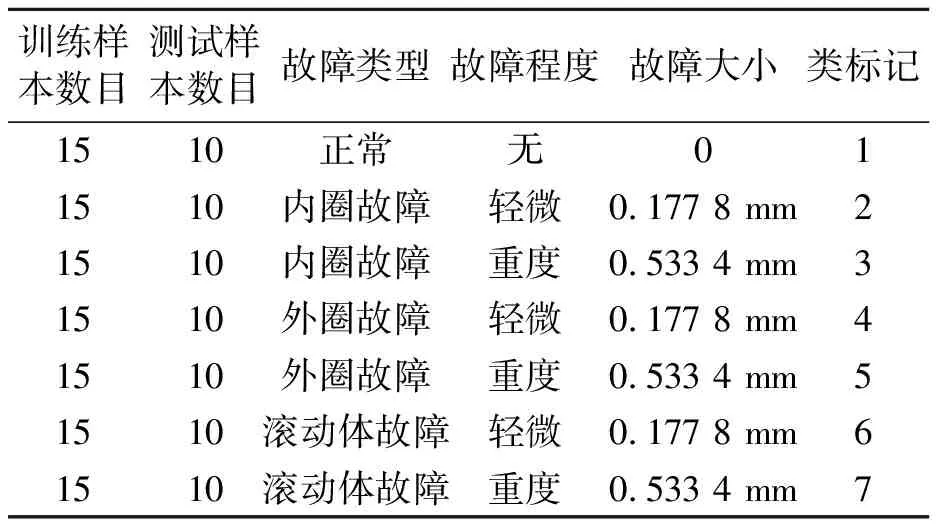
表1 实验数据类别描述
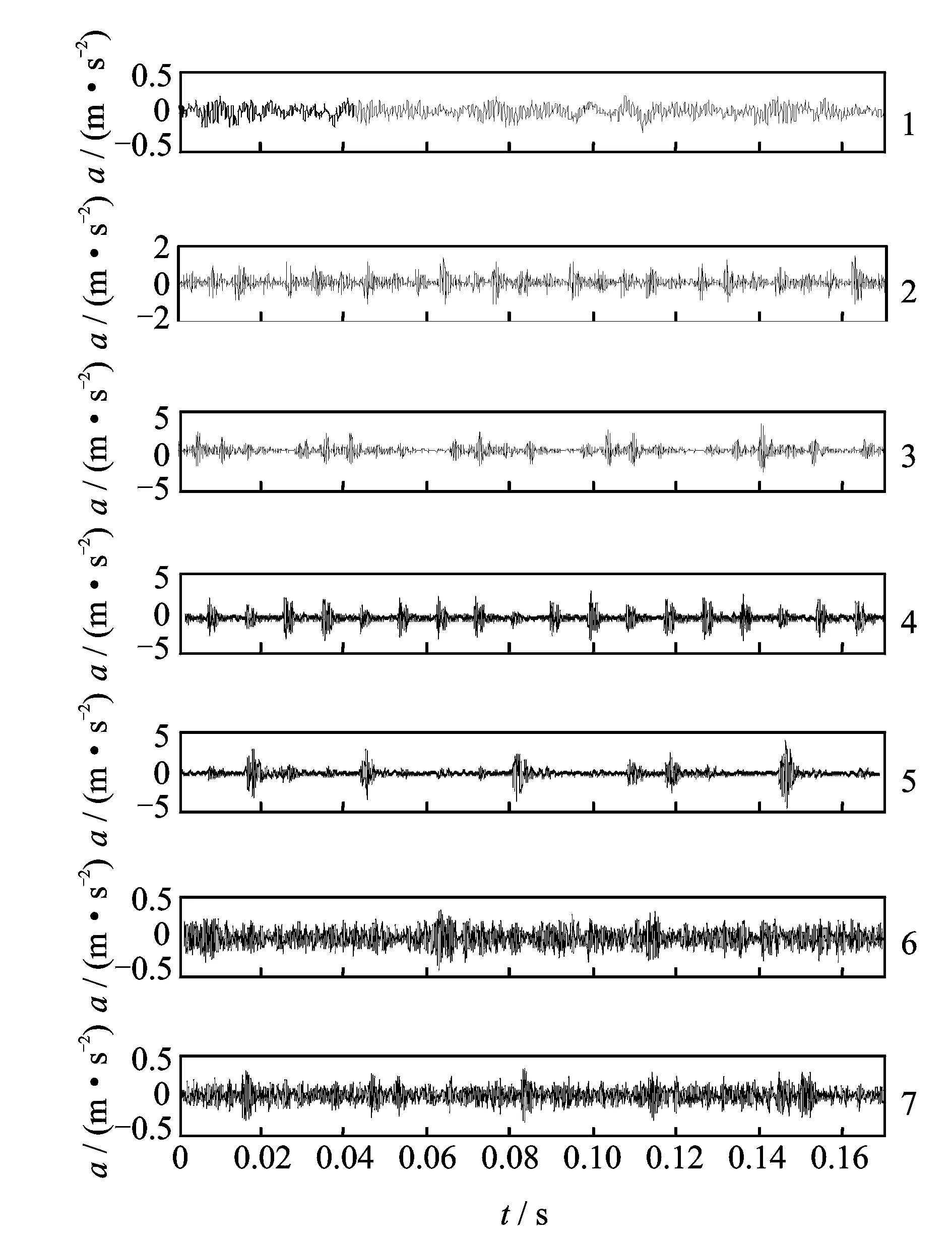
图7 正常和故障轴承振动信号的时域波形(图形右端数字对应表1中类标)
上述实验数据,故障类型分为外圈故障、内圈故障和滚动体故障;故障程度分为轻微故障和重度故障,加上正常,共7种类别,每一类取15个样本作为训练,取10个样本作为测试,共得到105个训练样本,70个测试样本。
首先,采用PELCD分别对每一类的每一个振动信号进行分解,每一个振动信号分解得到若干个ISC分量;
其次,提取前3个分量I1(t),I2(t)和I3(t)的上述特征参数和振动信号的时频熵,构建特征向量,T=[Ti]1×22。
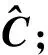
对于上述实验数据,LS由低到高的顺序为:
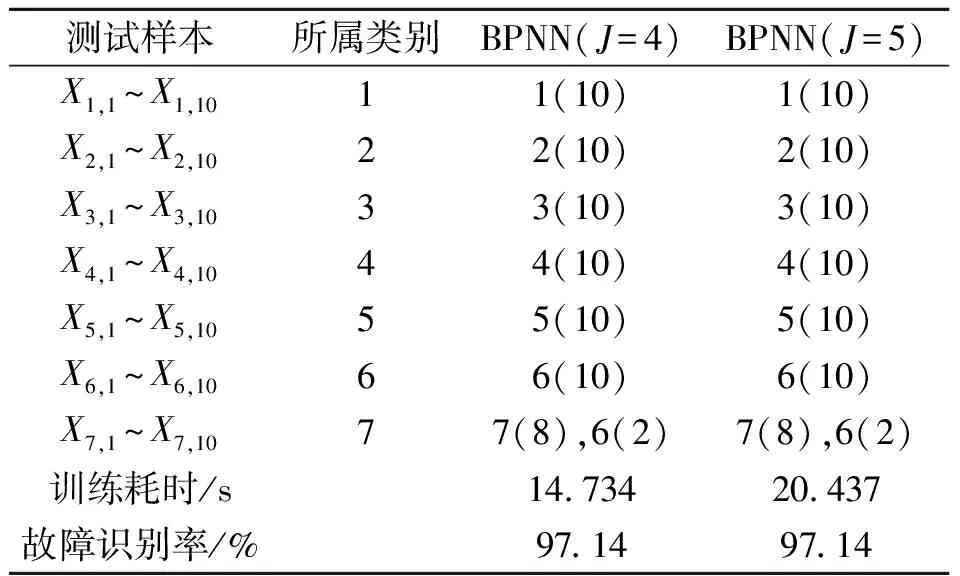
LS(T14) 即前5个最优特征值依次为:第一个分量I1(t)的重心频率,第一个分量I1(t)均方根频率,原始信号的时频熵,第一个分量I1(t)的脉冲指标,第二个分量I2(t)的均方根频率。这说明分解得到的第一个分量I1(t)包含了重要的故障信息,这与文献[10]的结果是一致的。此外原始信号的时频熵也能很好地反映故障特征变化。 显然特征向量的维数对诊断结果有重要的影响,如果特征向量的维数过小,即特征值个数较少,则无法完全反映和区分故障类型和故障程度,诊断效率不高;如果特征值个数较多会造成信息的冗余,训练耗时,降低诊断效率。为了比较,论文选择经过LS排序后前J个特征值(J=3,4,5,6,7)作为特征向量输入VPMCD分类器,训练样本和测试样本个数不变,经过训练建立预测模型,测试样本的输出结果,训练耗时及测试样本的识别率如表2所示。从表2中可以看出特征量个数对故障诊断结果的影响,特征量个数过多或过少都不宜;同时表2的结论也验证了论文提出的故障诊断模型中选择前5个特征量是可行且合理的。 表2 优化特征向量不同时测试样本的VPMCD输出结果 为了说明LS优化特征向量的必要性及优越性,论文选择未经过LS排序的前J个特征量(J=3,4,5)作为特征向量输入VPMCD分类器,训练样本和测试样本个数不变,经过训练建立预测模型,测试样本的输出结果,训练用时及测试样本的识别率如表3所示。对比表2和3易发现,由于特征向量未经过LS优化,对相同的VPMCD分类器,分别选择前4个和前5个特征值作为特征向量进行训练,测试样本的识别率明显要比经过LS优化后的特征向量作为输入特征向量的测试样本的识别率要低,这说明LS对特征值进行排序优化具有一定的优越性和必要性。 此外,为了说明VPMCD分类器的优越性,采用常用的BP神经网络(BPNN)分类器做同样的过程,其中网络结构为隐含层20层,输出层7层,训练目标为0.001,最大训练次数为6 000,其他参数为默认设置。特征向量分别由LS优化后的前4个和前5个特征值组成,训练样本和测试样本个数不变,通过训练BP分类器,测试样本的输出结果,训练用时及测试样本的识别率如表4所示。表4和2对比易发现:对于相同的特征向量,BPNN的识别率要低于VPMCD,且耗时较多,这说明VPMCD要优于BPNN,是一种有效的分类方法。 表3 特征量未LS优化时测试样本的VPMCD输出结果 表4 LS优化的特征量训练的BP神经网络的测试样本输出结果 提出了一种基于PELCD,LS和VPMCD的滚动轴承故障诊断模型。该模型具有以下优点: (1)PELCD克服了LCD分解的模态混淆问题,并对原PELCD方法中的参数进行了优化,使得PELCD分解对振动信号的分解结果更为精确,是一种有效的数据分析方法; (2)同时提取振动信号时域,频域和时频域的多个特征值,多角度反映故障特征; (3)针对提取特征值维数较多,容易造成信息冗余和维数灾难的问题,采用拉普拉斯分值特征选择降低特征向量维数,依据分值选择与故障关系最为密切的特征值,有效地降低了诊断时间,提高了诊断效率; (4)VPMCD通过对特征值间的内在关系进行预测,无需事先选择参数,自适应地选择最优预测模型实现模式的分类。实验数据表明,与BP神经网络相比,VPMCD在精确性和节约训练时间方面有一定的优越性。 参考文献: [1] 屈梁生,张海军.机械诊断中的几个基本问题[J].中国机械工程,2000,11(1/2):211—216.QU Liangsheng, ZHANG Haijun. Some basic problems in machinery diagnostics [J].China Mechanical Engineering,2000,11(1/2):211—216. [2] 于德介,程军圣,杨宇.机械故障诊断的Hilbert-Huang变换方法[M].北京:科学出版社,2006.Yu Dejie,Cheng Junsheng, Yang Yu. Mechanical Fault Diagnosis Method of Hilbert-Huang Transform[M]. Beijing: Science Press, 2006. [3] Huang N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc. Roy. Soc. London, A, 1998,454(1971):903—995. [4] Huang N E, Wu M C, LONG S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proc. R. Soc. Lond., A, 2003, 459 (2037):2 317—2 345. [5] Cheng Junsheng, Yu Dejie, Yang Yu. The application of energy operator demodulation approach based on EMD in machinery fault diagnosis[J]. Mechanical Systems and Signal Processing, 2007, 21(2): 668—677. [6] 雷亚国,何正嘉,訾艳阳.基于混合智能新模型的故障诊断[J],机械工程学报, 2008,44(7):112—117.LEI Yaguo, HE Zhengjia, ZI Yanyang. Fault diagnosis based on novel hybrid intelligent model[J]. Chinese Journal of Mechanical Engineering, 2008, 44(7):112—117. [7] 周智,朱永生,张优云,等. 基于EEMD 和共振解调的滚动轴承自适应故障诊断[J]. 振动与冲击,2013,32 (2):76—80.ZHOU Zhi, ZHU Yong-sheng, ZHANG You-yun,et al. Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance[J]. Journal of Vibration and Shock, 2013,32 (2): 76—80. [8] Yaguo Lei, Jing Lin, Zhengjia He, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery [J]. Mechanical Systems and Signal Processing, 2013, 35(1/2):108—126. [9] 程军圣,郑近德,杨宇. 一种新的非平稳信号分析方法-局部特征尺度分解法[J],振动工程学报,2012, 25(2): 215—220.CHENG Junsheng,ZHENG Jinde,YANG Yu. A new non-stationary signal analysis approach-the local characteristic-scale decomposition method[J].Journal of Vibration Engineering,2012,25(2):215—220. [10] 程军圣,郑近德,杨宇. 基于局部特征尺度分解的经验包络解调方法及其在机械故障诊断中的应用[J],机械工程学报,2012, 48(19):87—99.CHENG Junsheng, ZHENG Jinde, YANG Yu. Empirical envelope demodulation approach based on local characteristic-scale decomposition and its applications to mechanical fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2012, 48(19):87—99. [11] 郑近德, 程军圣, 杨宇. 部分集成局部特征尺度分解:一种新的基于噪声辅助数据分析方法[J]. 电子学报, 2013,41(5):1 030—1 035.ZHENG Jinde,CHENG Junsheng,YANG Yu. Partly ensemble local characteristic-scale decomposition: A new noise assisted data analysis method[J]. Acta Electronic Sinica,2013,41(5):1 030—1 035. [12] HE X F, CAI D, NIYOGI P. Laplacian score for feature selection[A]. Advances in Neural Information Processing System[C]. Cambridge,MA:MIT Press, 2005. [13] XIAO Y J, LI S, ZHANG D. Supervised and unsupervised parallel subspace learning for large scale image recognition[J]. Circuits and Systems for Video Technology, 2012, 22(10):1 497—1 511. [14] 李永强,刘杰,侯祥林,等. 人工神经网络的混合算法及其工程应用[J]. 机械工程学报, 2004,40(l):127—130.LI Yongqiang, LIU Jie, HOU Xianglin, et al. Mixed method of artificial neural network and its application of fault diagnosis for rotational machine[J]. Chinese Journal of Mechanical Engineering,2004,40(1):127—130. [15] WANG C C, YUAN K, SHEN P C, et al., Applications of fault diagnosis in rotating machinery by using time series analysis with neural network[J]. Expert Systems with Applications, 2010, 37(2):1 696—1 702. [16] RAFIEE J, TSE P W, HARIFI A, et al. A novel technique for selecting mother wavelet function using an intelligent fault diagnosis system[J]. Expert Systems with Applications, 2009, 36(3):4 862—4 875. [17] FEI S W, ZHANG X B. Fault diagnosis of power transformer based on support vector machine with genetic algorithm[J]. Expert Systems with Applications, 2009, 36(8):11 352—11 357. [18] Raghuraj R, Lakshminarayanan S. Variable predictive model based classification algorithm for effective separation of protein structural classes[J]. Computational Biology and Chemistry, 2008, 32(4): 302—306. [19] Raghuraj R, Lakshminarayanan S. VPMCD: Variable interaction modeling approach for class discrimination in biological systems[J]. FEBS Letters, 2007, 581(5/6): 826—830. [20] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17):174102-1-174102-4. [21] YAN R Q, LIU Y B, GAO R X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines[J]. Mech. Syst. Signal Process, 2012 (29): 474—484. [22] Lei Yaguo, He Zhegjia, Zi Yanyang, EEMD method and WNN for fault diagnosis of locomotive roller bearings[J]. Expert Systems with Applications, 2011, 38(6): 7 334—7 341. [23] 陈伟婷. 基于熵的表面肌电信号特征提取研究[D]. 上海:上海交通大学,2008.Chen Weiting, A study of feature extraction from SEMG signal based on entropy[D]. Shanghai:Shanghai Jiao Tong University, 2008. [24] 郑近德,程军圣,杨宇. 基于改进的ITD和模糊熵的滚动轴承故障诊断方法[J]. 中国机械工程,2012, 23 (19): 2 372—2 377.ZHENG Jinde, CHENG Junsheng YANG Yu. A rolling bearing fault diagnosis method based on Improved ITD and fuzzy entropy[J]. Chinese Mechanical Engineering, 2012, 23 (19): 2 372—2 377. [25] YU D J, YANG Y, CHENG J S, Application of time-frequency entropy method based on Hilbert-Huang transform to gear fault diagnosis[J], Measurement, 2007, 40: 823—830. [26] LEI Y G, HE Z J, ZI Y Y, A new approach to intelligent fault diagnosis of rotating machinery[J]. Expert Systems with Applications, 2008,35(4):1 593—1 600.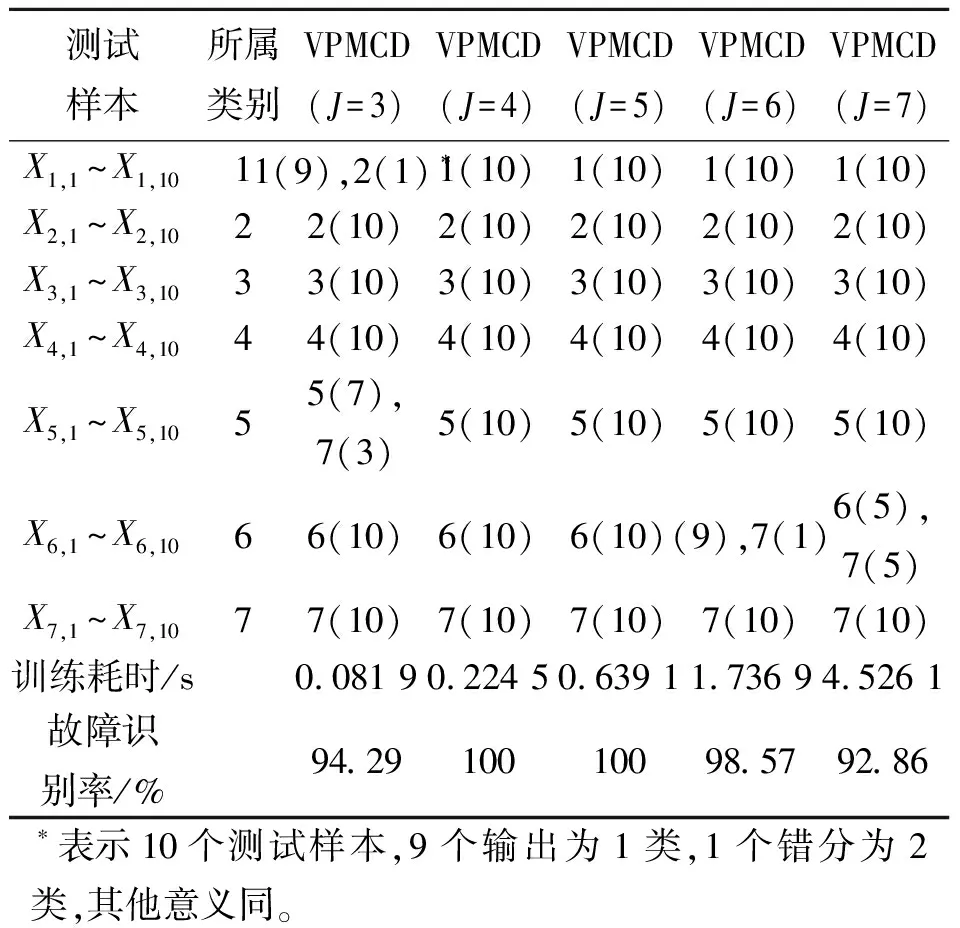

4 结 论

