波传播法求解低频激励下水中加端板圆柱壳的振动
陈美霞, 张 聪, 邓乃旗, 魏建辉, 谢 坤
(华中科技大学船舶与海洋工程学院, 湖北 武汉 430074)
引 言
水下噪声是限制海军装备性能的水下声音。在艇上安装的各种动力机械的不平衡力和力矩会产生振动和噪声,并引起与艇体相连接的结构单元振动。同时,低频时水是极好的传播介质。因此研究低频水中艇体的振动响应特性对于控制壳体航行噪声具有重要意义。
潜艇中部可以简化为圆柱壳并采用壳体理论进行分析[1]。国内外有很多学者对圆柱壳体的振动特性进行了研究,从不同边界条件下壳体的自由振动分析到不同端部结构的壳体的振动响应[2~5]。从计算方法上看,低频圆柱壳求解主要有模态叠加法和波传播法[6~8]。其中,模态叠加法通过已知边界条件设立位移函数,对圆柱壳的轴向、周向、径向位移进行叠加,并对运动方程积分求解。而波传播法将含待定系数的位移表达式代入运动方程,再通过两端的边界条件及结构之间的连续条件求解待定系数,从而求得其响应结果。因而波传播法可以灵活用于多种边界条件,并能通过增加连续条件处理端板、环肋加强、舱壁等附属结构及不连续结构。另外,Fuller和Tso研究了圆柱壳和圆板之间的连接作用[9,10],而邹明松等则重点研究了空气中两端圆板封闭的圆柱壳的自由振动特性[11]。对于水下圆柱壳体,Amabili和Paidoussis研究了有无流固耦合作用的壳体的振动特性[12],Fuller和Scott研究了内部流体和外部流体对圆柱壳体振动的影响[13,14],Caresta对水中不连续的加筋圆柱壳进行了具体的理论推导及响应分析[7]。
本文在以上文献的基础上,采用波传播法研究了水下加端板圆柱壳体的振动特性。与已有文献不同,本文重点着眼于激励及端板对圆柱壳体的影响。介绍了采用解析法求解带端板圆柱壳振动特性的方法,一定程度上揭示了端板对壳体振动的影响。本文研究中考虑了4种激励,即加载在端部圆板中心的轴对称载荷、加载在圆柱与圆板结合处的轴向和径向载荷、加载在圆柱中间的径向载荷,通过比较各激励作用下圆柱壳的振动特性,讨论了激励的方向和位置对振动响应的影响。此外,通过对比含端板和不含端板壳体的响应,讨论了端板对不同激励下壳体响应的影响。
1 水中加端板圆柱壳理论推导
1.1 水中圆柱壳振动分析
设x,θ和z分别为圆柱壳轴向、周向和径向的坐标轴,uc,vc和wc分别为三个方向的位移。壳体的长度为L,半径为a,厚度为hc。由Flügge理论可得圆柱壳的运动方程[1]。采用波传播法表示位移函数并求解圆柱壳振动的方法可以灵活用于多种边界条件,并能通过连续条件的建立实现加端板、加筋、加舱壁、加不同位置不同方向的载荷等,其表达式为[1]:
uc(x,θ,t)=Ucejknxcos(nθ)e-jωt
(1)
vc(x,θ,t)=Vcejknxsin(nθ)e-jωt
(2)
wc(x,θ,t)=Wcejknxcos(nθ)e-jωt
(3)
式中kn为壳体的轴向结构波数;ω为圆柱的圆频率。
对于水中的圆柱壳体,外部流体对圆柱壳产生外部压力,其表达式为[15]:
(4)
(5)
其中,
(6)
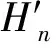
将位移函数(1)~(3)代入运动方程,可以得到AX=0,即:
(7)
由于系数行列式A的值必须为0,可以得到一个关于kn和ω的方程。对于每一个ω, 可以解得一个关于轴向结构波数kn的8次控制方程。本文采用搜索法求解轴向结构波数kn,步骤为:先解得空气中(即pa=0)的结构波数,得到4对共轭解,分别取出每对共轭解中的一个解,构成初始的4个解作为搜索起点。对于实数初始解,在实域范围内的初始解附近进行搜索,搜得能使控制方程为0的解。同理对于虚数初始解,在虚域范围内的初始解附近进行搜索。对于复数的初始解,将初始解分解为实部与虚部,即kn=kre+jkim。同样的,将控制方程也分解为实部与实部C=Cre+jCim,在初始附近解得同时能使控制方程实部和控制方程虚部为0的解,即将控制方程C=0化为{Cre=0;Cim=0}并求解。由于求法过程比较复杂,可以将流体项逐步增加并最后考虑含结构阻尼的杨氏模量Ec(1-jηs),其中ηs为结构阻尼,这样的搜索方式可以使求解过程更加准确。这种在复平面搜索复波数的数值方法简单且在低频范围内具有一定的准确性,但其搜索效率较低。尽管如此,在借助MATLAB 等计算软件的基础上进行求解,相比有限元软件如ANSYS计算求解水中壳体振动特性,在计算速度上还是具有很大优势的。另外,这种搜索方法在周向波数n较大时有漏根的可能,使用的时候需要根据具体的计算模型及频率范围调整其搜索范围和搜索间隔,以得到更为精确的计算结果。
1.2 端板振动分析
端板可以看作是有限圆板。圆板的运动方程为[10]:
(8)
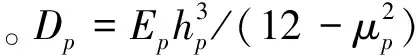
(11)
cos(nθ)e-jωt
(12)
sin(nθ)e-jωt
(13)
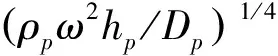
1.3 边界条件和连续条件
由1.1和1.2的推导可得,带端板圆柱壳共有12个待定系数,即8个圆柱壳的待定系数Wcn,i(i=1:8)和4个圆板待定系数Apn,i和Bpn,i(i=1,2)。因此可以通过边界条件和连续条件得到方程:BX=F,其中X为12个待定系数向量,F为外力向量。如图1所示,壳体在两端自由时,圆板和圆柱的位移、转角、内力和力矩在两端即x=0和L连接处的连续条件为:
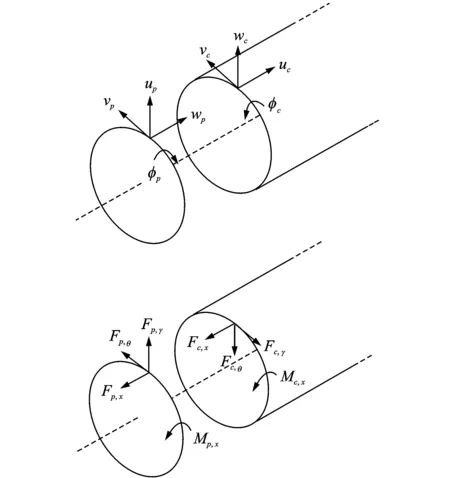
图1 圆柱壳和端板的位移、转角、内力和力矩
(14)
vp=vc
(15)
wp=uc
(16)
(17)
Fc,x+Fp,x=0
(18)
Fc,θ-Fp,θ=0
(19)
Mc,x+Mp,x=0
(20)
Fc,r-Fp,r=0
(21)
圆柱和圆板的内力和力矩表达式见参考文献[1,10]。
1.4 力激励
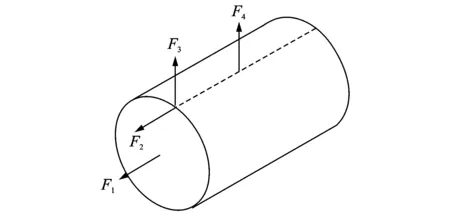
图2 壳体上的轴向、径向载荷
考虑不同位置不同方向轴向激励和径向激励对壳体响应的影响。如图2所示,F1为作用于端板中心的轴向力,是轴对称载荷,F2为作用于端板与圆柱连接处的轴向力,F3为作用于端板与圆柱连接处的径向力,F4为作用于壳体中点的径向力。
对于F1,求解方法是将端板分割成一个小圆板和一个环板,设小圆板的半径为a1,当a1足够小的时候,作用于端板中心的力可以看作是作用在小圆板边缘处,再通过小圆板和环板连接处的连续条件求解[16]。
对于F2,由于点激励作用在端板和圆柱壳的连接处,即(x0,θ0)=(0,0)。此时点激励可以用δ函数表示,在轴向方向,等式(18)化为
(22)
式中F0为点激励的振幅。等式两边同时乘以cos(nθ)并在周向从-π到π积分,得到[7]
Fc,x|x0+Fp,x|x0=εF0cos(nθ0)
(23)
其中,当n=0时,ε=1/(2πa),否则,ε=1/(πa)。
同理,对于F3,在径向方向,等式(21)化为
Fc,r|x0-Fp,r|x0=εF0cos(nθ0)
(24)
其中,当n=0时,ε=1/(2πa),否则,ε=1/(πa)。
对于F4,则在圆柱壳体加载荷的地方将圆柱壳分段,采用连接点处的位移、转角、内力和力矩的连续条件求解,且径向的内力之和为F4。
2 水中加端板圆柱壳振动响应及结果分析
加端板圆柱壳的几何尺寸为:圆柱壳的半径a=3.25 m,厚度hc=0.04 m,长度L=15 m。端板的厚度hp=0.04 m。壳体和端板的材料相同,密度为ρc=ρp=7 800 kg·m-3,杨氏模量Ec=Ep=2.1×1011N·m-2,泊松比μc=μp=0.3。结构阻尼ηs=0.02,因此复杨氏模量为E(1-jηs)。圆柱壳周围的流体密度为ρf=1 000 kg·m-3,流体速度cf=1 500 m·s-1。点激励振幅为单位力(F0=1 N),考虑4种激励,激励位置及方向如图3所示。为了比较不同激励下的柱壳响应,任取壳体上一点随频率变化的轴向位移及径向位移结果曲线进行对比,本节的位移曲线均来自于端部(x=0,θ=0)处的响应点,即与F1和F2激励点位置相同。
本文采用Ansys建有限元模型得到的数值法结果与解析法结果进行比较。其中,圆柱壳及端板采用shell63单元,流体用fluid30单元,流场边界单元用fluid130单元,流场与壳体结合处的节点及单元设置为具有流固耦合特性的节点及单元。
2.1 流体对传播波波数的影响
由1.1可以得知,求解水中壳体的结构波数时,需要先解得空气中的结构波数,得到四对共轭解,分别取出每对共轭解中的一个解,构成初始的四个解作为搜索起点,这四个初始解中含一个实数解、一个虚数解和两个复数解。通过搜索得到水中壳体的结构波数,得到新的实数解、虚数解和复数解。为了讨论流体对结构波数的影响,现以复数解的实部和虚部为代表,比较空气中的结构波数和水中结构波数随频率变化的结果曲线,对比结果如图3所示。
从图3可以看出,对于n=0和n=1模态,水中壳体结构波数的实部在较低频率下与空气中壳体结构波数实部相等,随着频率升高,两者差距逐渐加大且水中壳体的结构波数的实部大于空气中的,相反的,水中壳体的结构波数的虚部小于空气中的。同时,流体对n=0模态下结构波数的影响比对n=1模态下结构波数的影响大,尤其是对于n=1模态下结构波数的虚部,流体的影响非常小。
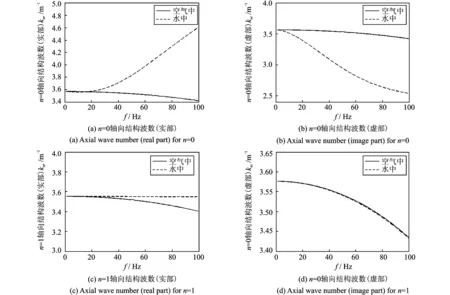
图3 空气中、水中壳体结构波数求解比较
2.2 点激励的方向和位置对壳体振动响应的影响
在4种载荷下,壳体的响应如图4~7所示。首先,从图4~7中波传播法求解得到的轴向位移、径向位移与数值法结果的对比可以看出,两种方法得到的结果曲线吻合情况较好,但依然存在一定误差,这主要是由于两种方法对流体载荷的处理不一样造成的,解析法将流体近似处理成无限区域内的压力,而数值法将用有限元方法对流体进行建模并将结合处单元设为流固耦合属性。但是,从整体上看,两者的结果曲线趋势一致,由此可以证明,解析法得出的结果是可信的。
图4是在端板中心轴向激励F1作用下,壳体在轴向和径向上的响应位移。由于F1是轴对称载荷,主要引起端板和圆柱壳的呼吸模态。
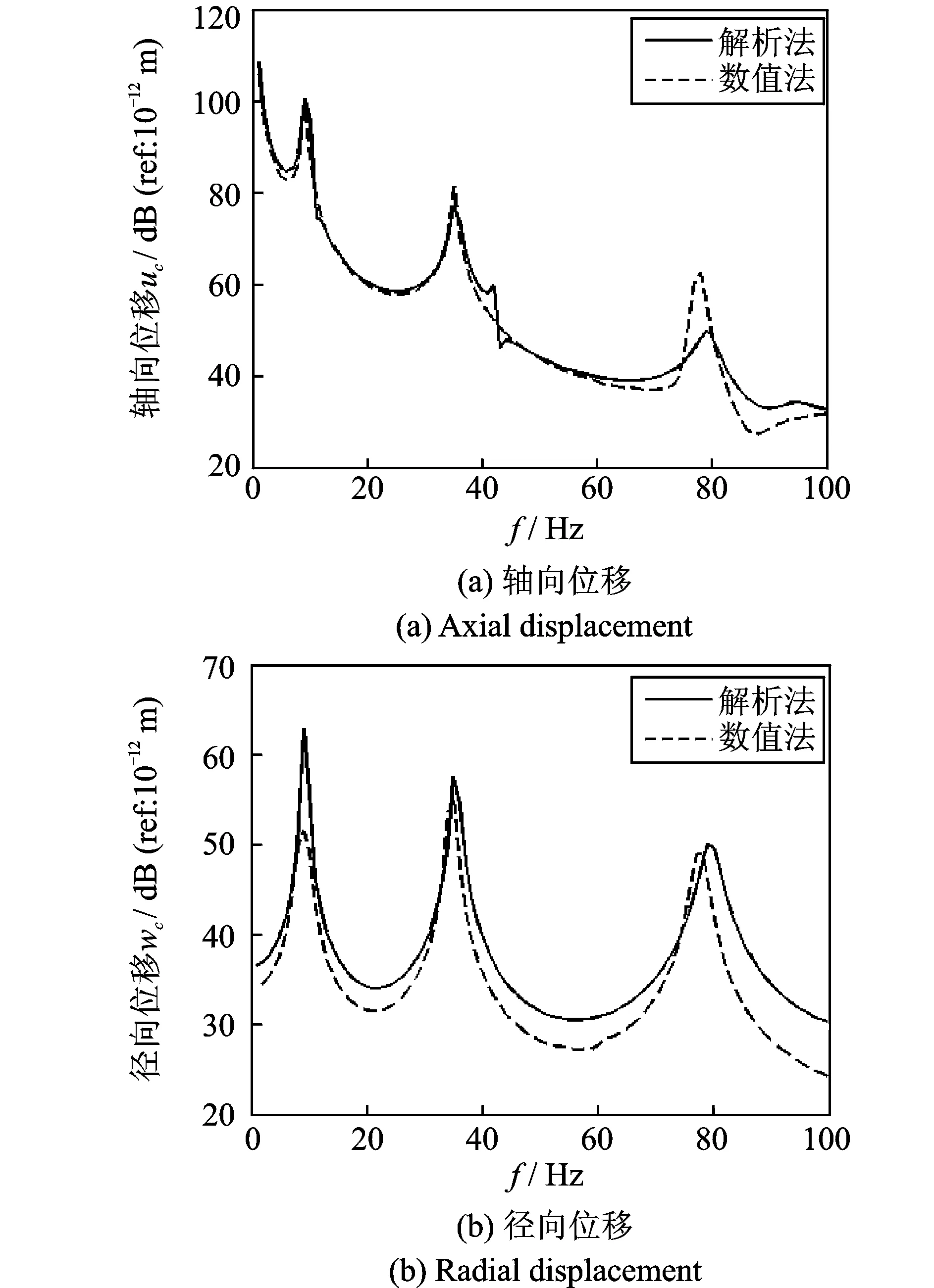
图4 轴向激励在端板中心时(F1),壳体的响应
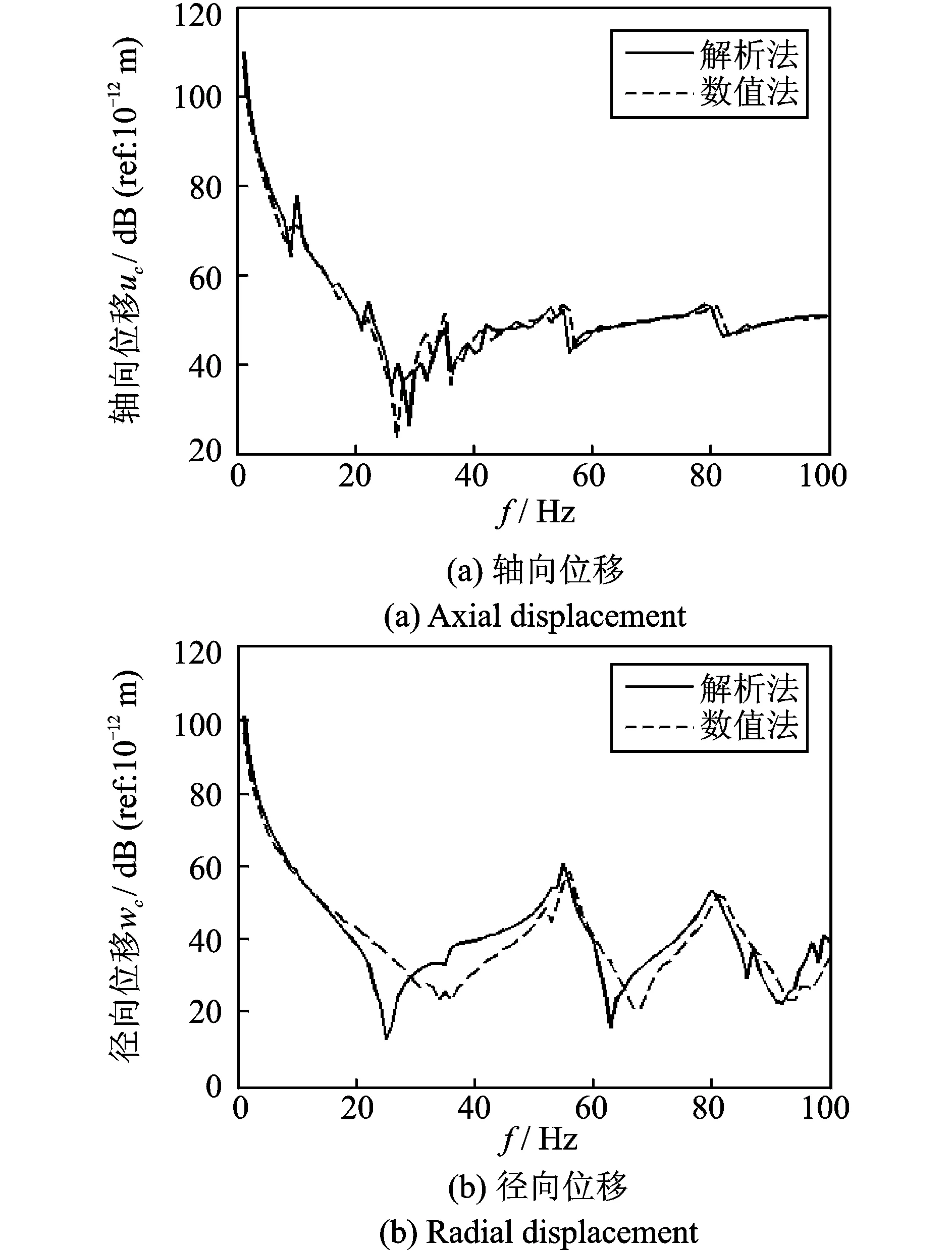
图5 轴向激励在端板与圆柱连接处时(F2),壳体的响应
图5是在端板与圆柱连接处轴向激励F2作用下壳体在轴向和径向上的位移响应。从计算结果可得,当把轴向载荷从端板的中心移到边缘以后,此时点激励不再是轴对称激励,因此除了呼吸模态外,还能引起各个不同周向模态下的振动,在100 Hz以内的频率范围内,轴向方向响应以n=0:3的运动为主,而在径向方向,主要引起n=1弯曲模态的运动。同时,端板的运动与圆柱相比十分微小。
图6是在端板与圆柱连接处径向激励F3作用下壳体在轴向和径向上的位移响应。从计算结果可以得出,此时点激励激起的轴向运动及径向运动在100 Hz范围内均主要来自弯曲模态n=1。与图7相比较,可以看出当将端板与圆柱连接处的激励由轴向方向变为径向方向以后,径向方向位移曲线波峰位置变化不大,即主要为来自于n=1的运动,而在轴向方向,n≠1的运动被弱化,弯曲模态下的运动占到了绝对主要的位置。
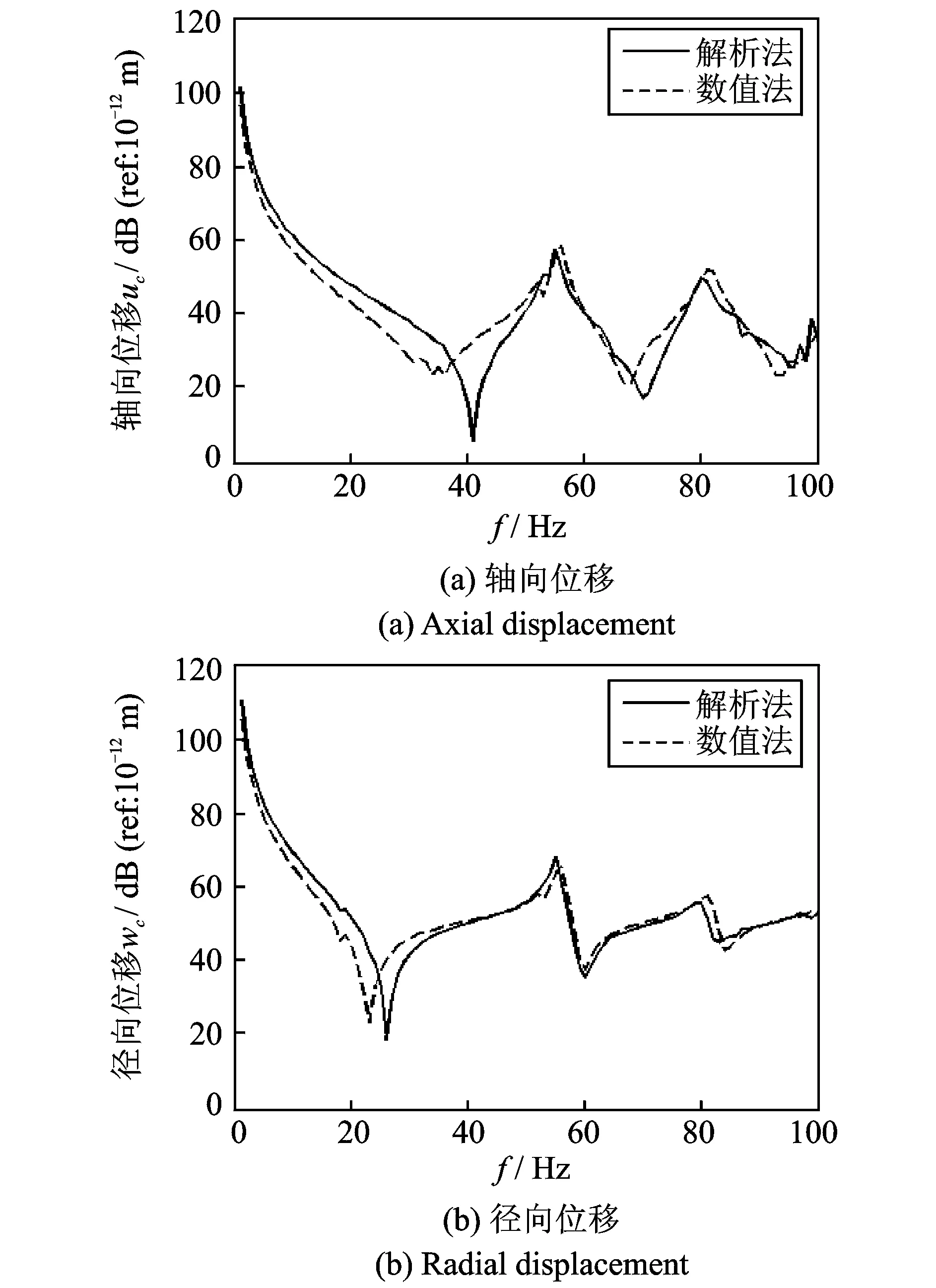
图6 径向激励在端板与圆柱连接处时(F3),壳体的响应
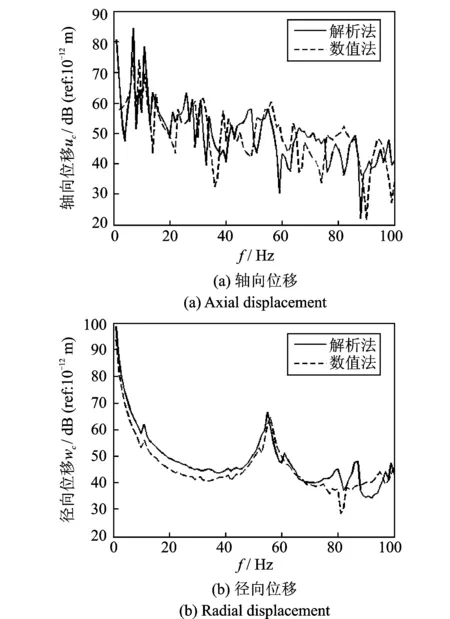
图7 径向激励在圆柱壳中间时(F4),壳体的响应
图7是在圆柱L/2处径向激励F4作用下壳体在轴向和径向上的位移响应。将径向激励从圆柱的端部移到中部以后,点激励不再只激起n=1模态的位移,而是激起了各个模态下的运动,且波峰数目显著增加。在轴向方向,各个模态下位移的峰值大小相似,而径向位移在100 Hz范围内以n=1:2模态为主,其中,径向位移中幅值较小的几个峰值是端板的固有振动引起的,由此可见,在这种载荷下,端板的位移跟圆柱壳幅值大小相当但略小,这点在2.3节端板的影响中会详细讨论。
总之,通过以上结果的对比可以看出,当激励的位置发生改变的时候,壳体的位移响应曲线也发生相应改变,无论是在轴向上还是径向上,不同模态下壳体的位移在总位移中所占的比例有较大变化,曲线的趋势及峰值位置也都不同。而对于同样位置的激励,不同的激励方向对位移响应的影响相对较小,主要改变某一方向上的位移,如文中端部的轴向激励和径向激励下的壳体位移相比,轴向上相差较大,而径向上位移的峰值位置和各模态下位移在总位移中的比重均相似。
2.3 端板对壳体振动响应的影响
由于F1作用在端板中心,无法讨论端板对这种载荷下壳体响应的影响,因此该部分只讨论端板在F2,F3和F4激励作用下对壳体响应的影响。本节中如无特殊说明,计算的响应位移为n=0∶10的合位移。
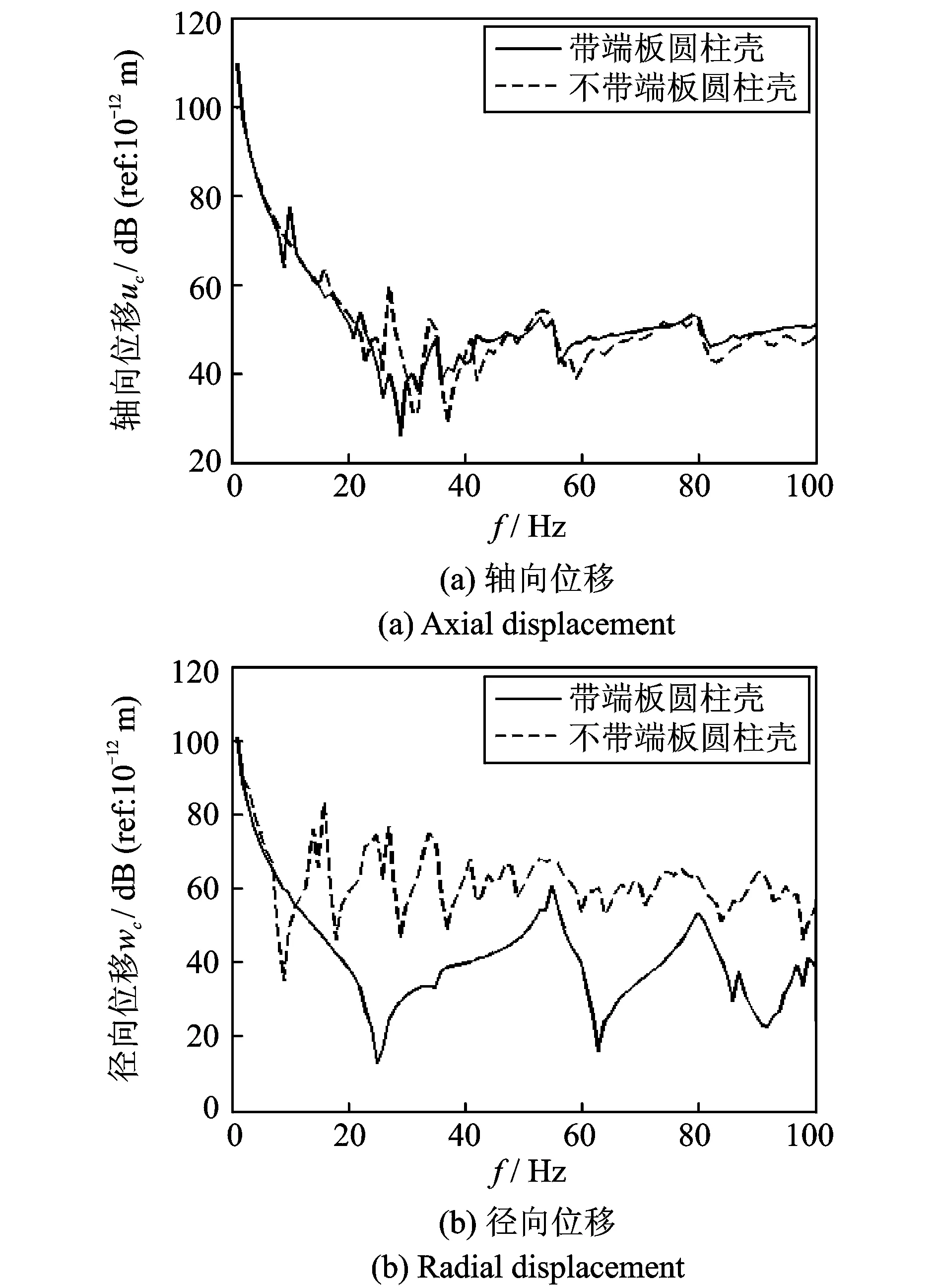
图8 F2激励下,加端板与不加端板的响应比较
图8是F2载荷下加端板与不加端板壳体的位移响应曲线的对比结果。由图中可知,在轴向激励下,端板对径向位移的影响远大于对轴向位移的影响。没有端板的壳体的径向位移在波峰的数目和振幅上都大于有端板的壳体。这主要是由于端板对径向位移的束缚造成的。分解到不同周向模态下,取n=1和n=2的结果如图9和10所示。
从图9和10可以看出,n=1时,端板对轴向位移和径向位移影响并不大。但是n=2时,首先,由于端板的自身重量,使得位移的波峰向低频方向平移,同时,端板减小了轴向位移在较高频率范围内的幅值,并大幅度减小了径向位移的幅值。并且不含端板时,轴向激励激起的位移不再主要由n=0:3组成,高阶各模态的位移与低阶模态位移幅值相当。总的来说,端板主要抑制了高阶模态振动,并以抑制径向振动更为明显。
图11为F3载荷下轴向位移和径向位移的对比结果。由图中可知,端板减小了轴向和径向位移的幅值大小并减少了波峰数目,换言之,端板从整体上减弱了该激励的作用。分解到不同周向模态下,取n=1和n=2的结果如图12和13所示。
从图12和13可以看出,与轴向激励下不同,在径向激励下,n=1时,轴向位移受端板影响不大,但径向位移曲线的非波峰处及较高频的波峰处的幅值均略有减小。而n=2时,端板使轴向位移和径向位移的位移值都大幅减小,径向位移固有频率处的波峰已不明显。因此,在径向激励下,端板抑制位移的作用更为明显,各阶模态下位移都受到其影响,而端板对径向位移的影响依然大于对轴向位移的影响。
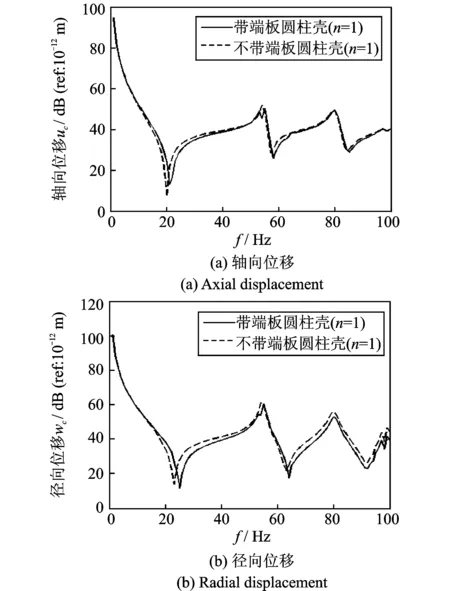
图9 F2激励下,加端板与不加端板n=1模态下响应比较
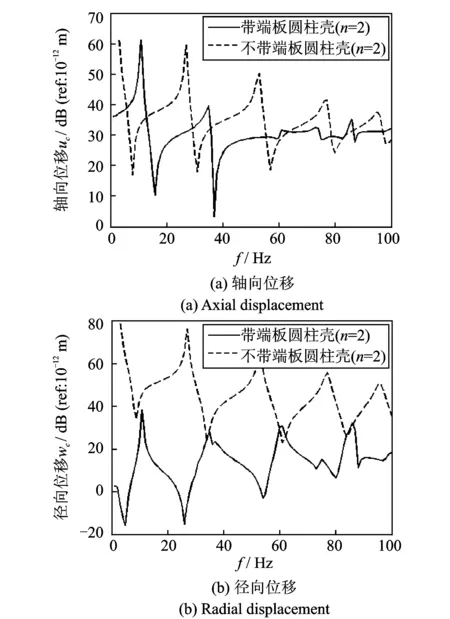
图10 F2激励下,加端板与不加端板n=2模态下响应比较
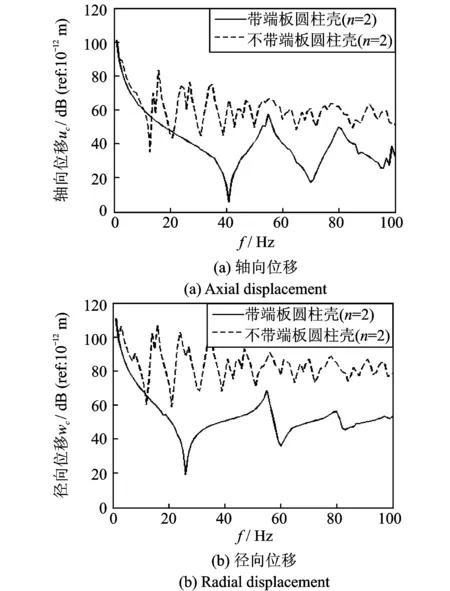
图11 F3激励下,加端板与不加端板的响应比较
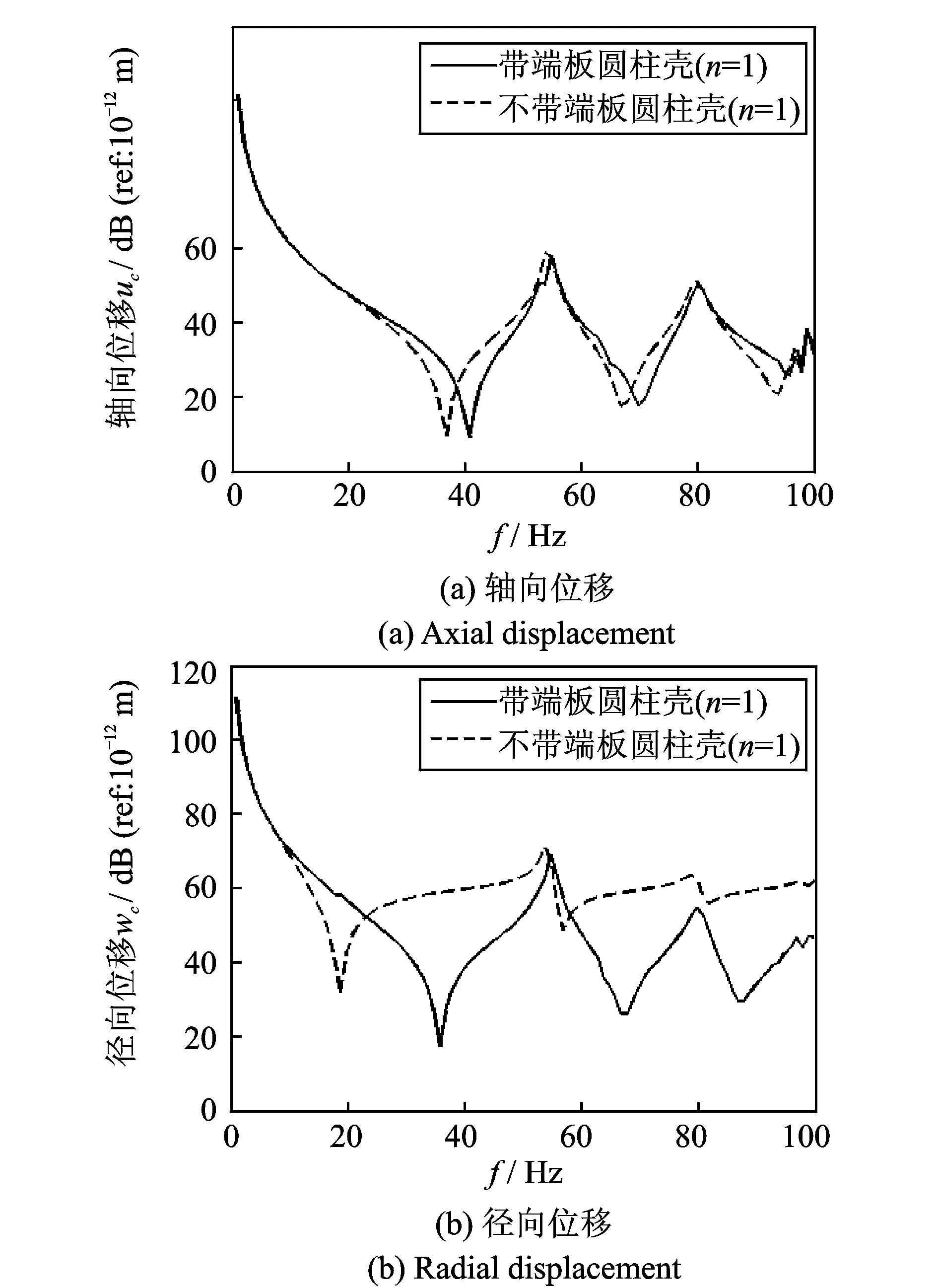
图12 F3激励下,加端板与不加端板n=1模态下响应比较

图13 F3激励下,加端板与不加端板n=2模态下响应比较
图14为F4载荷下轴向位移和径向位移的对比结果。与前两种载荷相似,端板使得波峰变多并且位移响应幅值减小,其中以减小径向位移的效果更为明显。分解到不同周向模态下,取n=1和n=2的结果如图15和16所示。
由图15和16可知,径向激励在壳体中部时,n=1下的峰值位置和峰值大小并无显著改变,但是加端板模型的位移响应结果多了一些峰值,可见这些峰值是载荷激起的端板的振动,从n=2的比较结果也可以看到同样的特征。这一现象在前两种激励下并不明显,这是由于激励在端板上时,端板的n=1,n=2等模态下的运动远远小于壳体的运动,而激励移到壳体中部以后,壳体带动端板一起进行振动,因此端板弯曲模态以及其他高阶模态的位移增大。除此之外,从n=2的结果可以看到,端板在高阶的时候同样起到了抑制振动从而减小位移幅值的作用,并且抑制作用在径向位移上更为明显,同时,由于端板的自身重量使得峰值向低频方向移动。
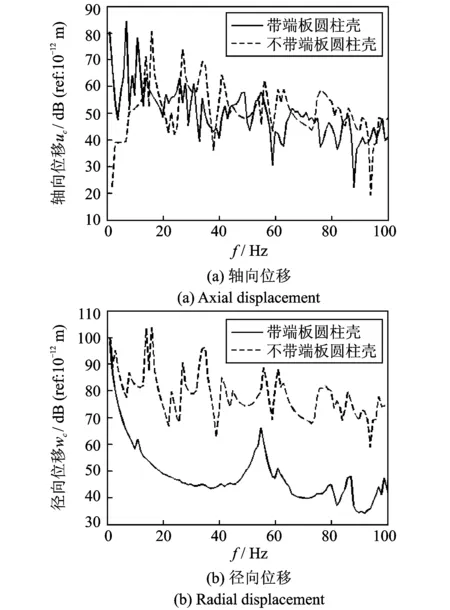
图14 F4激励下,加端板与不加端板的响应比较
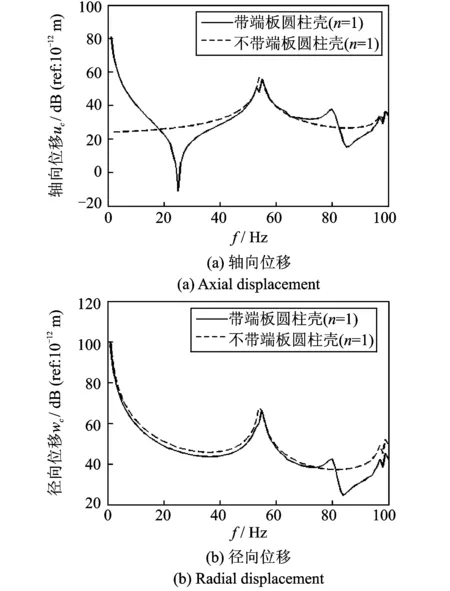
图15 F4激励下,加端板与不加端板n=1模态下响应比较
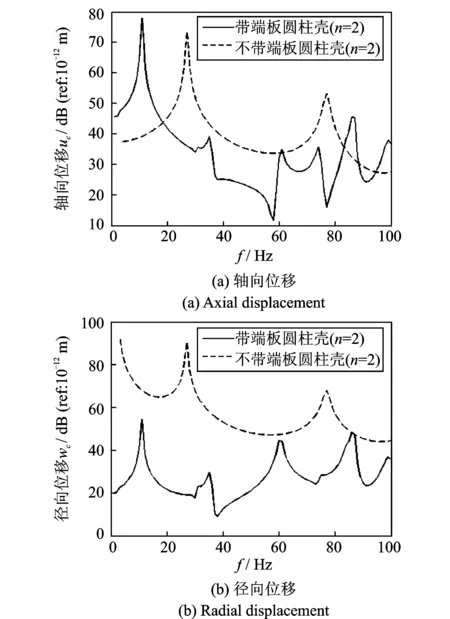
图16 F4激励下,加端板与不加端板n=2模态下响应比较
从以上各激励下壳体含端板和不含端板的结果曲线对比可以看出,由于端板与圆柱壳连接时对其径向变形的限制,因此端板对高阶的径向位移的抑制作用非常明显;对于作用在端板与圆柱结合处上的径向载荷,由于端板的限制作用对径向载荷有一定抵消,因此端板的存在使得响应位移整体减小;而对于作用在圆柱壳中间部位的载荷,端板不仅减小了位移曲线峰值大小,还增加了曲线波峰的数目,这些波峰对应的频率是端板的固有频率。另外,值得一提的是,本文采用的端板与圆柱壳材料相同,即刚性较小,如果采用刚性较大的端板,除了主要抑制径向位移以外,还会使壳体端部与端板连接处难以发生形变,其分析方法与本文类似。
3 结 论
本文介绍了如何采用波传播法求解低频时水中加端板圆柱壳的运动,其中,圆柱壳采用搜索法求得结构波数的复数根,端板和圆柱壳之间采用连续条件方程求解。本文讨论了不同方向与位置的激励下壳体的动响应特性,并分析了不同激励下端板的对水中壳体动响应的影响,带端板的圆柱壳结构的设计及某一舱段结构振动分析有一定工程意义。得出的结论如下:
1) 随着频率升高,水中壳体的结构波数的实部逐渐大于空气中的,而水中壳体的结构波数的虚部逐渐小于空气中的。同时,流体对n=0模态下结构波数的影响比对n=1模态下结构波数的影响大。
2) 通过将波传播法求解水中加端板圆柱壳的响应结果与数值法计算结果对比,证明了该方法的正确性与可行性。
3) 激励的位置对壳体的位移响应影响较大,轴向及径向的位移曲线的趋势及峰值位置均发生改变,且各模态下位移在总位移中所占的比例有较大变化。而激励的方向对位移响应的影响相对较小,主要改变某一方向上的位移曲线特征。
4) 于作用在端板与圆柱壳连接处的载荷,端板主要抑制了高阶的径向位移。而对于作用在圆柱壳中间部位的载荷,端板不仅减小了位移曲线峰值大小,还增加了端板在其固有频率处的峰值,即在这种激励下,端板振动幅值与圆柱的幅值相差不大。
参考文献:
[1] Leissa A W. Vibration of Shells, American Institute of Physics[M]. New York: American Institute of Physics, 1993:1—30
[2] Yu Y Y. Free vibrations of thin cylindrical shells having finite lengths with freely supported and clamped edges[J]. Journal of Applied Mechanics,1955, 22: 547—552.
[3] Cheng L, Nicholas J. Free vibration analysis of a cylindrical shell-circular plate system with 6 general coupling and various boundary conditions[J]. Journal of Sound and Vibration 155, 1992, 2: 231—247.
[4] Galletly G D, Mistry J. The free vibrations of cylindrical shells with various end closures[J]. Nuclear Engineering and Design, 1974, 30(2): 249—268.
[5] Pan X, Tso Y, Juniper R. Active control of radiated pressure of a submarine hull[J]. Journal of Sound and Vibration, 2008, 311 (1/2): 224—242.
[6] 周锋,骆东平,蔡敏波,等. 有限长环肋圆柱壳低阶模态声辐射性能分析[J]. 应用科技, 2004, 31(9): 38—41.Zhou Feng, Luo Dongping, Cai Minbo, et al. Sound radiation analysis of low order modes from the ring-stiffened cylindrical shells in fluid medium[J]. Applied Science and Technology, 2004, 31(9): 38—41.
[7] Caresta M, Kessissoglou N J. Structural and acoustic responses of a fluid-loaded cylindrical hull with structural discontinuities[J]. Applied Acoustics, 2009, 70(7): 954—963.
[8] Caresta M, Kessissoglou N J. Acoustic signature of a submarine hull under harmonic excitation[J]. Applied Acoustics, 2010, 71: 17—31.
[9] Fuller C R. The effect of wall discontinuities on the propagation of flexural waves in cylindrical shells[J]. Journal of Sound and Vibration, 1981, 75: 207—228.
[10] Tso Y K, Hansen C H. Wave propagation through cylinder/plate junctions[J]. Journal of Sound and Vibration, 1995, 186 (3): 447—461.
[11] 邹明松,吴文伟,孙建刚,等. 两端圆板封闭圆柱壳自由振动的半解析解[J]. 船舶力学, 2012, 16(11): 1 306—1 313.Zou Mingsong, Wu Wenwei, Sun Jiangang, et al. A semianalytical solution for free vibration of a cylindrical shell with two end plates [J]. Jounral of Ship Mechanics, 2012, 16(11): 1 306—1 313.
[12] Amabili M, Paidoussis M P. Review of studies on geometrically nonlinear vibrations and dynamics of circular cylindrical shells and panels, with and without fluid structure interaction[J]. Applied Mechanics Reviews, 2003,56 (4) : 349—381.
[13] Fuller C R, Fahy F J. Characteristics of wave propagation and energy distribution in cylindrical elastic shells filled with fluid[J]. Journal of Sound and Vibration, 1982, 81(4):501—518.
[14] Scott J F M. The free modes of propagation of an infinite fluid-loaded thin cylindrical shell[J]. Journal of Sound and Vibration, 1988, 125 (2): 241—280.
[15] Junger M C, Feit D. Sound, Structures, and Their Interaction[M]. 2nd ed. Cambridge: MIT Press, 1986: 168—181.
[16] Caresta M, Kessissoglou N J. Reduction of hull-radiated noise using vibroacoustic optimization of the propulsion system[J]. Journal of Ship Research, 2011, 55 (3): 149—162.

