稀疏信号分解-分段拟合逼近及其无转速计阶比应用

梅检民， 肖云魁， 曾锐利， 赵慧敏，崔 鲲

(1.军事交通学院军用车辆系， 天津 300161；2.天津大学机械工程学院 天津 300072；3.军事交通学院训练部， 天津 300161)

引 言

阶比跟踪是工程实际中常用的旋转机械变转速过程信号分析方法，其基本思想是对满足平稳性要求的等角度采样信号进行频谱分析，关键是要根据转速信息将等时间采样信号重采样成等角度采样信号，当不具备转速脉冲信号时，应用受限。无转速计阶比分析根据振动信号估计转速信息[1～4]，再等角度重采样，该方法不需要安装转速采集装置，能分析现场没有同步采集转速信号的离线振动信号，因此在旋转机械变转速过程分析中得到越来越广泛的应用[5～7]。

无转速计阶比分析的精度不如有转速计阶比分析，其影响因素有两个：一是根据振动信号估计的瞬时频率；二是根据估计的瞬时频率计算的重采样时刻。目前估计瞬时频率方法是：通过搜索旋转机械振动信号的时频谱图峰值获得某个阶比分量的瞬时频率[1,8]，进而得到所需要的参考轴转速，分析精度受到频率分辨率的限制；基于多尺度线调频基的稀疏信号分解方法能有效分解频率呈曲线变化的多分量信号，并估计瞬时频率，在文献[9～12]中的应用效果良好。计算重采样时刻主要通过多项式拟合频率函数，求解拟合频率积分方程计算等角度时刻[6,13]，当拟合精度不高或方程较复杂时，有时会出现无解、无实数解的现象。

为了解决上述问题，本文提出了一种基于分数阶傅里叶变换(Fractional Fourier Transform, FRFT)多尺度线调频基稀疏信号分解的自适应分段方法，对分段内信号采用2阶多项式拟合频率函数，提高拟合精度，构建积分逼近方法代替方程求解确定等角度重采样时刻，解决方程无解、无实数解对阶比计算的影响等问题。仿真和实测信号应用表明，基于稀疏信号分解和分段拟合积分逼近的无转速计阶比方法分析效果令人满意。

1 无转速计阶比分析原理及存在问题

1.1 无转速计阶比分析原理

无转速计阶比分析方法根据估计出的瞬时频率，计算等角度采样时刻，通过插值实现等角度重采样，具体实现过程如下[5]:

(1)采用瞬时频率估计方法，估计出参考轴瞬时频率，对该瞬时频率进行多项式拟合，假设采用3阶多项式拟合，则有

f(t)=at3+bt2+ct+d

(1)

(2)确定最大分析阶次Omax；

(3)计算等角度采样间隔Δθ，依据采样定理，等角度采样率需大于或等于最大分析阶次的两倍，因此

(2)

(4)计算重采样后数据的长度N

(3)

式中T为采样总时间，f(t)为频率拟合函数。

(5)计算重采样时刻Tn

式中T0为时间起点。求方程(5)的有效解，即可求得等角度重采样时刻Tn。

(6)根据Tn对振动信号进行插值，获得等角度采样信号，再进行FFT变换，得到无转速计的阶比谱。

1.2 存在问题

从上述无转速计阶比分析原理可以看出，传统无转速阶比方法的两个关键步骤如下：

(1)对瞬时频率进行多项式拟合确定瞬时频率函数。传统无转速计阶比方法，多采用单一多项式对整个时间范围进行拟合，多项式阶次越低，拟合精度较差，多项式阶次越高，拟合精度有所提高，但方程(5)越复杂；分段拟合能降低拟合阶次并保证拟合精度，但如何进行分段才能使分数段数量最少和拟合精度到达最好，是需要解决的关键问题。

(2)求解拟合频率积分方程(4)的实数解确定等角度重采样时刻。拟合多项式阶次越高，方程(5)越复杂，越容易出现无解、无实数解等情况，导致得不到等角度采样时刻，或等角度重采样时刻不准确。

因此传统的无转速计阶比方法存在低阶多项式拟合精度差，高阶拟合频率积分方程难求解的问题，导致阶比分析无结果，或分析结果精度低。

2 基于稀疏信号分解和分段拟合积分逼近的无转速计阶比分析方法

2.1 基于FRFT的多尺度线调频基稀疏信号分解

分数阶傅里叶变换可以解释为信号在时频平面内绕原点旋转任意角度后所构成的分数阶域上的表示[14]，设某个线性调频(Linear Frequency Modulation,LFM)分量的时频分布与时间轴的夹角β，如图1所示。只要分数阶傅里叶变换的旋转角度α与β正交，则该LFM信号会聚集在分数阶傅里叶域u0一点上，此时的α为FRFT最佳旋转角度，对应的阶次p=2α/π为FRFT最佳阶次。所以，按照一定阶次步长Δp，对信号连续进行p∈[0,2]的FRFT，如果信号具有LFM特性，就会在分数阶域坐标u和分数阶次p构成的(p,u)平面上出现峰值，如图2所示，实现LFM信号的检测。

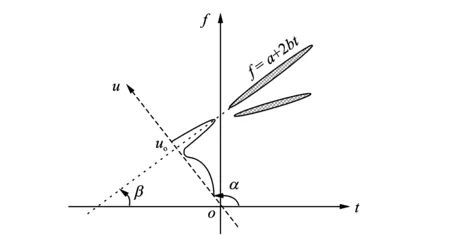
图1 LFM信号在分数阶域的能量聚集性

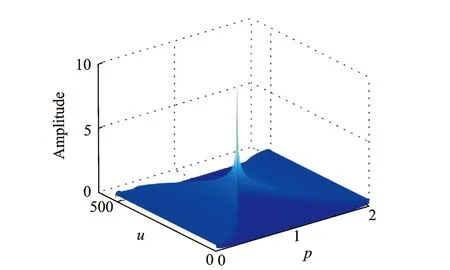
图2 LFM信号FRFT幅度谱

基于FRFT确定基函数的多尺度线调频基稀疏信号分解方法(Multi-scale chirplet sparse signal decomposition based on FRFT, MSCSD_FRFT)，具体分解流程如下：

(1)将长度为N的分析信号x(t)在不同的尺度系数j下，以N2-j为长度进行等分，形成动态时间支撑区集合I=[kN2-j～(k+1)N2-j]，动态时间支撑区长度必须大于32，长度太小影响分析结果，所以j=0,1,…,log2N-5为分析尺度系数，k=0,1,…,2j-1；

(2)对各动态时间支撑区内的信号xI(t)的FRFT幅值谱搜索峰值，确定基函数。如图2中峰值点位置(p0,u0)，结合图1中最佳阶次、分数阶域聚集点与频率偏置a、频率斜率2b的坐标关系，经过反归一化处理[7]，得到该动态时间支撑区基函数的频率偏置a和频率斜率2b为

(6)

式中fs为离散观测数据的采样频率，t0为观测时间，根据a，2b确定最佳基函数为

ha,b,I(t)=Ka,b,Ie-i(at+bt2)lI(t)

(7)

式中Ka,b,I为归一化系数，使得‖ha,b,I‖=1；lI(t)为矩形窗函数，当t∈I时为1，当t∉I时为0；

(3)将动态时间支撑区内的信号xI(t)向该区间的基函数ha,b,I(t)投影得到投影系数βI，定义该动态时间支撑区下的分解信号为cI(t)：

βI=[xI(t),ha,b,I(t)]≈re-iφ/2

(8)

cI(t)=2|βI|e-i(at+bt2-angle(2βI))lI(t)

(9)

可见，分解信号cI(t)保留了信号的初始相位、幅值和频率信息；

(4)连接动态时间支撑区，搜寻使分解信号能量最大的动态时间支撑区连接方法[15]，通过该连接方法形成的信号分量即为本次分解的信号分量；

(5)将分析信号减去分解信号分量，形成残余信号；

(6)判断残余信号能量与分析信号能量之比是否小于终止分解阈值，若大于终止阈值，则将残余信号作为新的分解信号重复(2)～(5)步，如果小于终止阈值则停止分解。

2.2 分段拟合确定频率函数

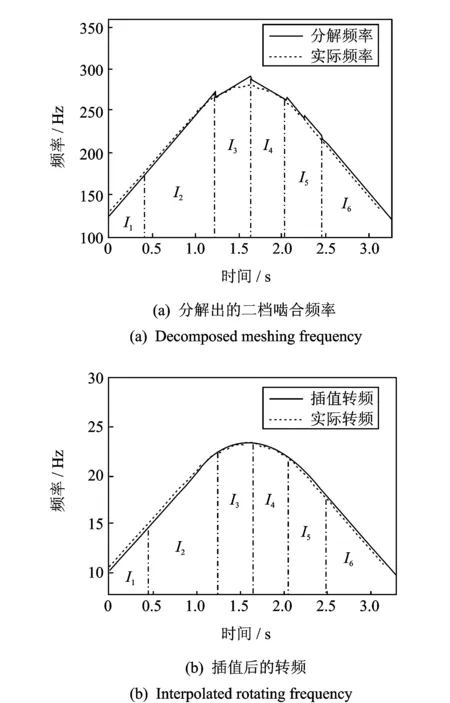
图3 基于稀疏信号分解的分段拟合

采集BJ2020S变速器置二档变速过程振动信号，以输入轴为参考的二档啮合频率阶比为12.03，采样频率40 kHz，采样时间3.287 6 s。对振动信号进行基于FRFT的多尺度线调频基稀疏信号分解，分解出的二档啮合频率曲线如图3(a)所示。可以看出基于FRFT的多尺度线调频基稀疏信号分解在频率变化简单区间选择大尺度基函数分解，在频率变化复杂区间选择小尺度基函数分解，分解出的啮合频率较好地吻合了实际频率特征。分解啮合频率对应I1,I2,…,I6动态时间支撑区，由于各区间线性调频基函数的瞬时频率都是斜直线，在各区间端点连接处出现了锯齿波动，为了更好地贴近实际频率，对各区间分解频率中间点进行三次样条插值，根据插值后的啮合频率和阶比，计算出插值后的瞬时转频(啮合频率/12.03)，结果如图3(b)所示，插值后的瞬时转频能更好地贴近实际转频。

从图3可以看出，变速器变转速过程频率呈曲线不规则变化，不同的变转速过程，频率曲线变化也会不同。传统无转速计阶比方法采用单个多项式对频率区间进行整体拟合，在整体趋势和局部特征上难以两全；当频率变化复杂时，即使多项式阶次很高，也难以贴近频率变化特征拟合，而且对于不同信号，必须重新选择合适的多项式阶次，缺乏自适应性，工程实用性差。如果采用分段拟合，会适当降低拟合多项式阶次并保证拟合精度，但如何根据频率变化特征，自适应合理分段是需要解决的关键问题。

分析图3(b)发现，在啮合频率分解信号对应的动态时间支撑区I1,I2,…,I6内，转频曲线变化比较简单，有利于采用低阶多项式准确拟合。因此，本文提出了一种基于FRFT多尺度线调频基稀疏信号分解的分段拟合方法，即根据稀疏信号分解出的啮合频率信号对应的动态时间支撑区对插值后的转频曲线进行分段，在各分段内采用二阶多项式拟合转频曲线，得到转频的分段拟合函数。该分段拟合方法的优点在于：

(1)无论频率如何复杂变化，基于FRFT的多尺度线调频基稀疏信号分解都能贴近信号频率变化特点自适应地将信号分解在不同尺度的动态时间支撑区内，根据该动态时间支撑区对转频进行分段，既能保证各段内信号频率变化简单，又能使分段数最少；

(2)分段内频率曲线近似线性变化，采用二阶多项式就能准确拟合；对于不同的变转速过程信号，稀疏信号分解都能将信号自适应分段成频率变化简单的若干段，不需要重新选择合适的多项式阶次，采用二阶多项式都能准确拟合，提高了工程实用性。

因此，基于FRFT多尺度线调频基稀疏信号分解的分段拟合方法是一种自适应寻优分段拟合方法，有效克服了单个多项式整体拟合精度不高和自适应差的问题，为分段拟合方法的合理分段探索了新的有效途径。

2.3 积分逼近求解等角度采样时刻

按照无转速计阶比分析原理，确定了频率拟合函数fi(t)，就可以计算等角度重采样时刻。要求图4所示的区间Ii内的等角度重采样时刻Tn，需要求解拟合频率积分方程(10)中的实数解。当函数fi(t)阶次较高时，会使其原函数Fi(t)阶次较高，从而不容易求解以下方程，甚至没有实数解，得不到准确的重采样时刻Tn。

图4 区间Ii的积分逼近

(10)

式中fi(t)为区间Ii内的拟合频率函数，Nθi为区间Ii内的等角度采样点数，可由下式求出。

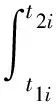
(11)

式中t1i,t2i为区间Ii的时间起点和终点，Δθ为等角度采样间隔。

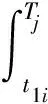
(12)

设区间Ii内数据点数为N，等时间采样间隔为ts，将Ii细化等分成M份，令ts′=ts/M，逐一计算时刻Tj=t1i+jts′,j=1,2,…,MN下的积分值q(j)为

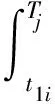
(13)

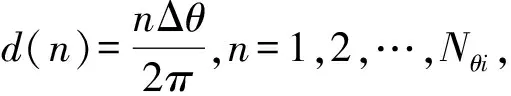
n=1,2,…,Nθi

(14)

式(14)表明q(kn)与d(n)最接近，两者相差Δn，则可近似认为Tkn就是区间Ii内第n个等角度重采样时刻，即Tn=Tkn，为了更准确地逼近Tn，可以调整细化倍数M，M的选择可权衡精度和计算量确定。以上就是基于积分逼近求解等角度重采样时刻的原理，该方法不需要求解复杂方程，计算简单、实现方便，无论频率如何复杂变化，该方法都能求出等角度重采样时刻，有效解决了拟合频率积分方程难求解和方程无实数解对阶比分析的影响。

综合以上分析，归纳整理得基于稀疏信号分解和分段拟合积分逼近的无转速计阶比(Order spectrum with no tachometer based on MSCSD_FRFT and segmental fitting-integral approach，OSNT_MSFIA)算法流程如下：

(1)采用基于FRFT的多尺度线调频基稀疏信号分解对振动信号进行分解，对分解出的啮合频率中间点进行三次样条插值，根据插值后的啮合频率计算瞬时转频；

(2)根据啮合频率对应的动态时间支撑区Ii,i=1,2,…，NI(NI为分解频率对应的动态时间支撑区个数)，对瞬时转频进行分段，并在各段内进行2多项式拟合，得出转频分段函数fi(t)；

(3)确定最大分析阶次Omax，计算等角度采样间隔Δθ≤π/Omax；

(4)计算区间Ii内等角度重采样后数据点数Nθi；

(5)积分逼近求解等角度重采样时刻Tn=Tkn；

(6)根据Tn对振动信号进行插值，实现等角度重采样，对等角度重采样后信号进行FFT，得到基于稀疏信号分解和分段拟合积分逼近的无转速计阶比谱。

3 仿真分析

本算例以频率曲线变化的仿真信号，验证基于单个多项式整体拟合并求解拟合频率积分方程确定等角度重采样时刻的传统阶比谱的局限性，检验基于稀疏信号分解和分段拟合积分逼近的新阶比的正确性和准确性。设仿真信号为

x=[cos(4π(t6+2t3/3+3t2+30t))+1]×1.5cos(10π(t6+2t3/3+3t2+30t))

(15)

仿真转频为

f(t)=t5+2t2+6t+30

(16)

仿真齿数为5，信号x被2倍转频调制，信号中包含阶比为3，5，7的三个阶比分量。采样频率为1 024 Hz，采样点数为2 048点。对仿真信号x进行基于FRFT的多尺度线调频基稀疏信号分解，分解出的啮合频率曲线如图5(a)中实线所示，与实际啮合频率较好吻合；中间点插值后的啮合频率如图5(b)中实线所示，很好地贴近了实际啮合频率。

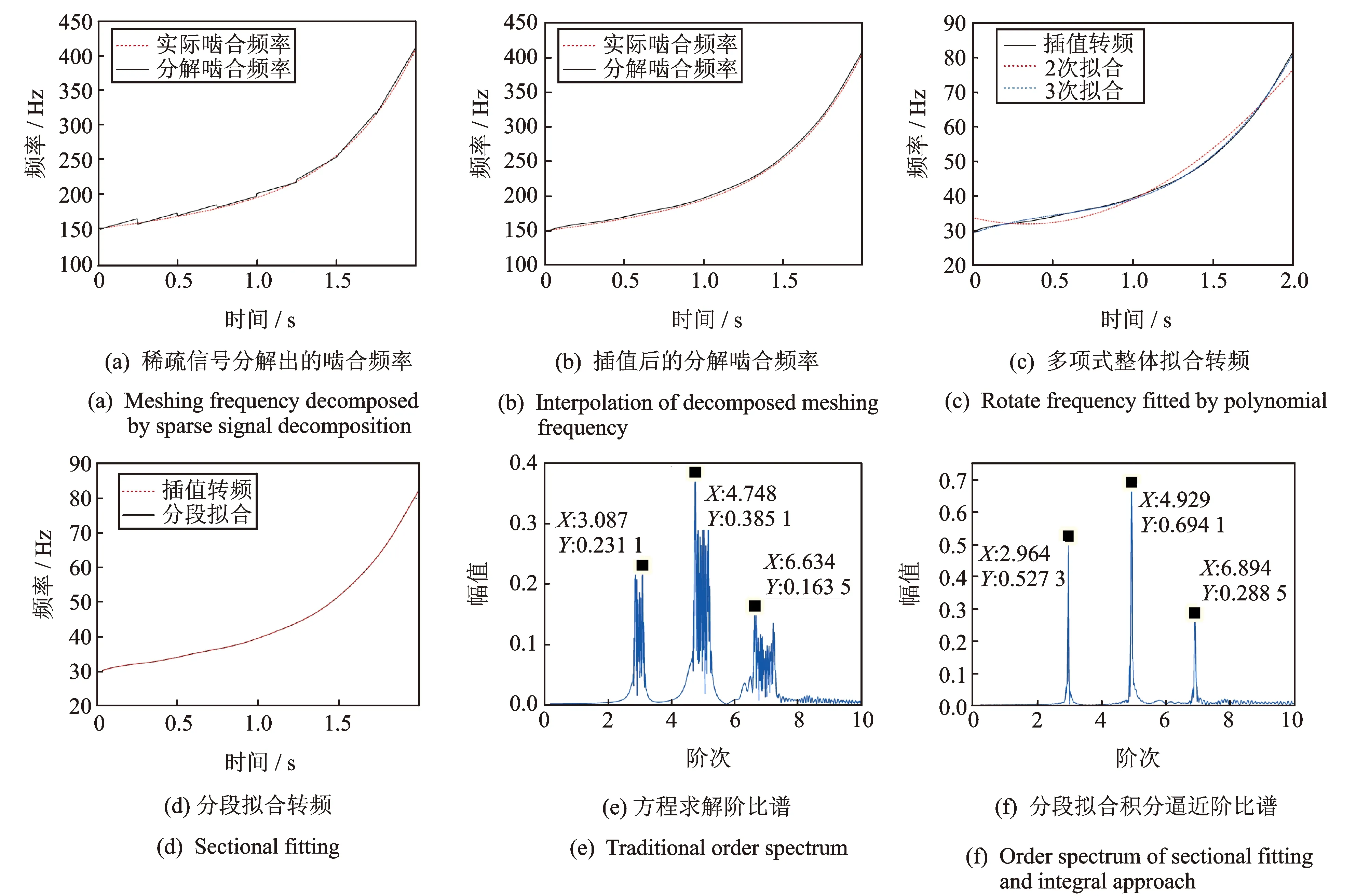
图5 方程求解阶比谱和分段拟合积分逼近阶比谱对比

根据插值啮合频率和仿真齿数计算出插值转频，分别对插值转频进行2，3阶多项式整体拟合，结果如图5(c)所示；根据分解啮合频率对应的动态时间支撑区，对插值转频进行分段，在各段内用2阶多项式进行拟合，分段拟合结果如图5(d)中虚线所示，整体拟合和分段拟合的误差(绝对误差)分析如表1所示。

结合图5(c),(d)和表1可以看出，整体拟合时2阶多项式拟合误差较大，3阶多项式拟合效果较好；分段拟合的结果几乎与插值频率重合，误差最小，证明了基于稀疏信号分解的分段拟合的准确性。

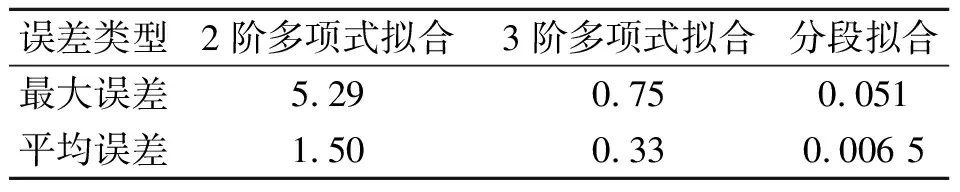
表1 单一多项式整体拟合与分段拟合误差分析

根据2阶多项式整体拟合结果计算阶比谱，结果如图5(e)所示。图中3个峰值阶次为3.087，4.748和6.634，与理论阶次3，5，7相差较大，这是2阶多项式拟合精度低造成的阶次模糊现象；根据3阶多项式整体拟合结果计算阶比谱，在求解个别等角度时刻时出现了方程无解或复数解，无法得到阶比谱。可见，基于单个多项式整体拟合和求解拟合频率积分方程的阶比方法具有局限性，即低阶多项式拟合精度低，阶次模糊，高阶多项式拟合精度高，拟合频率积分方程难求解。

根据基于稀疏信号分解的分段拟合结果进行积分逼近，求取等角度重采样时刻，计算阶比谱，结果如图5(f)所示，图中2.964，4.929，6.894三个阶比峰值独立而突出，分别对应理论阶次3，5，7。证明了基于稀疏信号分解和分段拟合积分逼近的无转速计阶比的正确性和准确性。

4 实例应用

试验对象为BJ2020S变速器输出轴轴承，试验装置构成如图6所示。电动机模拟发动机驱动变速器，发电机模拟负载。输出轴承型号为50307，采用电火花在轴承外圈上加工坑点模拟早期剥落故障，以输入轴为参考轴，外圈故障特征阶比为1.132。采样频率40 kHz，采样时间3.287 6 s。

图6 试验装置构成

为了验证本方法分析实测振动信号的效果，对BJ2020S变速器置二档时的变转速过程振动信号进行分析。分解出的二档啮合频率曲线如图7(a)所示；根据插值后的分解啮合频率计算出瞬时转频，结果如图7(b)所示，很好地贴近了实际转频；对瞬时频率进行2，3，4阶多项式整体拟合，结果如图7(c)所示，都没能很好地贴近瞬时转频，尤其是在端点处误差更大。由于低阶多项式拟合的阶比谱会出现阶次模糊，高阶拟合频率积分方程难求解，无法得到阶比谱，因此无法对传统阶比谱进行解调判断轴承有无故障。为了更好地检验本文方法的有效性，将基于稀疏信号分解和分段拟合积分逼近的阶比解调谱与有转速计的实际阶比解调谱进行对比。

图7 实测信号分段拟合积分逼近阶比谱

对瞬时转频进行基于稀疏信号分解的分段拟合，结果如图7(d)所示，分段拟合频率很好地吻合了瞬时频率，证明了分段拟合的准确性；根据分段拟合结果，对各区间进行积分逼近求取等角度重采样时刻，对等角度重采样信号进行阶比解调分析，结果如图7(e)所示，图中1.135及其倍频阶次处出现明显峰值，与外圈特征阶次1.132非常接近，有效提取出了外圈故障特征阶次；根据转速脉冲信号计算的阶比解调谱如图7(f)所示，图中1.133及其倍频阶次处出现明显峰值，与外圈故障特征阶次1.132对应，可见图7(e)，(f)都有效反映了外圈故障特征阶次信息，证明了基于稀疏信号分解和分段拟合积分逼近的无转速计阶比方法分析实测信号的有效性，虽然与有转速计阶比相比精度略有差异，但已经能满足故障特征提取要求。

5 结 论

(1)根据稀疏信号分解啮合频率对应的动态时间支撑区对转频进行分段，各区间内频率变化简单，分段数最少，是一种自适应寻优分段方法；

(2)在啮合频率分解区间内瞬时转频变化简单，只需要采用2多项式就能准确拟合，无论频率如何复杂变化，该方法都能高精度拟合，对于不同信号不需要重复选择合适的多项式阶次，有效解决了单个多项式整体拟合精度不高、缺乏自适应性的问题；

(3)求解拟合频率积分方程确定等角度重采样时刻，受方程有无根、有无实根的影响，不易获取准确等角度重采样时刻，影响阶比分析精度；采用积分逼近方法，不需要求解方程，对任意信号都能求出等角度重采样时刻，有效解决了方程根影响等角度重采样时刻的问题；

(4)瞬时频率准确估计和等角度时刻准确计算是无转速计阶比分析的关键步骤，基于稀疏信号分解的分段拟合积分逼近能更准确实现两个关键步骤，为无转速计条件下旋转机械变转速过程阶比分析探索了一条新途径。

参考文献：

[1] 郭瑜，秦树人，汤宝平，等.基于瞬时频率估计的旋转机械阶比跟踪[J].机械工程学报，2003,39(3):32—36.Guo Yu, Qin Shuren, Tang Baoping, et al. Order tracking of rotating machinery based on instantaneous frequency estimation[J]. Chinese Journal of Mechanical Engineering, 2003,39(3):32—36.

[2] 郭瑜，秦树人.无转速计旋转机械升降速振动信号零相位阶比跟踪滤波[J].机械工程学报，2004,40(3):50—54.Guo Yu, Qin Shuren. Tacholess order tracking filtering for run-up or coast down vibration signal of rotating machinery based on zero-phase distortion digital filtering[J]. Chinese Journal of Mechanical Engineering, 2004,40(3):50—54.

[3] Yang J M,Qin S R,Zhong J, et a1.Development of virtual instrument in characteristic analysis of rotating machinery based on instantaneous frequency estimation[J].Chinese Journal of Mechanical Engineering,2004,17(4):490—493.

[4] Wu J D,Huang C W,Huang R W.An application of a recursive Kalman filtering algorithm in rotating machinery fault diagnosis[J].NDT & E International,2004, 37(5):411—419.

[5] 任凌志，于德介，彭富强，等.基于多尺度线调频基稀疏信号分解的齿轮故障信号阶比分析[J]. 机械工程学报，2011,47(13):92—97.Ren Lingzhi, Yu Dejie, Peng Fuqiang, et al. Order analysis of gear fault signals based on multi-scale chirplet and sparse signal decomposition[J]. Chinese Journal of Mechanical Engineering, 2011,47(13):92—97.

[6] 陈向民，于德介，任凌志，等. 基于线调频小波路径追踪阶比能量解调的齿轮轮齿裂纹故障诊断[J]. 中国机械工程，2011,22(11):2 598—2 603.Chen Xiangmin, Yu Dejie, Ren Lingzhi, et al. Order energy demodulating approach based on chirplet path pursuit and its application to gear tooth crack fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2011, 22(11):2 598—2 603.

[7] 邓蕾，傅炜娜，董绍江，等. 无转速计的旋转机械Vold-Kalman阶比跟踪研究[J]. 振动与冲击，2011,30(3):5—9.Deng Lei, Fu Weina, Dong Shaojiang, et al. Tacholess Vold-Kalman order tracking of rotating machinery[J]. Journal of Vibration and Shock, 2011,30(3):5—9.

[8] 赵晓平，张令弥，郭勤涛.基于瞬时频率估计的自适应Vold-Kalman阶比跟踪研究[J].振动与冲击，2008, 27 (12):112—116.Zhao Xiaoping, Zhang Lingmi, Guo Qintao. Adaptive Vold-Kalman order tracking based on instantaneous frequency estimation[J].Journal of Vibration and Shock, 2011,30(3):5—9.

[9] 彭富强，于德介，刘坚. 一种基于多尺度线调频基的稀疏信号分解方法[J]. 振动工程学报，2010，23(3):333—338.Peng Fu-qiang, Yu De-jie, Liu Jian. Sparse signal decomposition method based on multi-scale chirplet[J]. Journal of Vibration Engineering , 2010,23(3):333—338.

[10] 彭富强，于德介，罗洁思. 基于多尺度线调频基稀疏信号分解的齿轮故障诊断[J]. 中国机械工程，2009,20(14):1 726—1 730.Peng Fu-qiang, Yu De-jie, Luo Jie-si. Sparse signal decomposition method based on multi-scale chirplet and its application to gear fault diagnosis [J]. Chinese Journal of Mechanical Engineering, 2009,20(14):1 726—1 730.

[11] 任凌志，于德介. 基于多尺度线调频基稀疏信号分解的齿轮故障信号阶比分析[J]. 机械工程学报，2011,47(13):92—97.Ren Ling-zhi, Yu De-jie. Order analysis of gear fault signals based on multi-scale chirplet and sparse signal decomposition [J]. Journal of Mechanical Engineering, 2011,47(13):92—97.

[12] 彭富强，于德介. 基于多尺度线调频基稀疏信号分解的轴承故障诊断[J]. 机械工程学报，2010,46(7):88—94.Peng Fu-qiang, Yu De-jie. Sparse signal decomposition method based on multi-scale chirplet and its application to bearing fault diagnosis [J]. Journal of Mechanical Engineering, 2010,46(7):88—94.

[13] 皮维，于德介，彭富强，等. 基于多尺度线调频基稀疏信号分解的包络阶次谱在齿轮故障诊断中的应用[J]. 中国机械工程，2011,22(1):69—73.Pi Wei, Yu Dejie, Peng Fuqiang, et al. Application of envelope order spectrum based on multi-scale chirplet and sparse signal decomposition to gearbox fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2011,22(1):69—73.

[14] 陶然. 分数阶傅里叶变换及其应用[M].北京：清华大学出版社，2009:3—7.Tao Ran. Fractional Fourier Transform and Its Applications[M]. Beijing: Tsinghua University Press, 2009:3—7.

[15] Candès E J, Charlton P R, Helgason H. Detecting highly oscillatory signals by chirplet path pursuit[J]. Applied and Computational Harmonic Analysis, 2008,24(1):14—40.