颗粒阻尼技术在制动鼓减振方面的应用研究
夏兆旺, 魏守贝, 温华兵, 刘献栋
(1.江苏科技大学能源与动力工程学院, 江苏 镇江 212003; 2.北京航空航天大学交通科学与工程学院, 北京 100191)
引 言
颗粒阻尼减振器是含有颗粒的孔腔结构,其孔腔可以有多种形式,可以是在现有结构适当位置加工出一系列孔腔,也可以是附加在结构上的独立腔体[1~3]。颗粒阻尼器的减振机理是利用颗粒间的摩擦和碰撞消耗系统的能量,达到降低系统振动的目的,具有强非线性[4,5]。颗粒阻尼是一种有效的减振降噪方法,并被成功用于航空航天和工业领域恶劣环境下设备的减振降噪。Panossian等[6]研究了颗粒密度等参数对带颗粒阻尼器的梁结构和航天飞机主发动机进口分流叶片的振动影响。研究结果表明颗粒阻尼减振技术能适应高温等恶劣环境下结构的减振。近年来,颗粒阻尼减振技术被应用于航空、汽车等领域的减振研究[7~9]。但目前,还未见颗粒阻尼技术应用于旋转制动鼓减振降噪的研究报道。
作者前期对颗粒阻尼技术的耦合仿真算法进行了研究[10]。本文将在耦合仿真算法的基础上,重点分析带颗粒阻尼器的旋转结构振动特性。研究颗粒阻尼用于处于离心力作用下的汽车制动鼓减振降噪,同时分析颗粒密度、填充率、激振力频率和幅值等参数对减振效果的影响。考虑到旋转状态制动鼓测试的复杂性,静态的制动鼓试验测试将用于验证仿真算法。论文拓展了颗粒阻尼技术的应用范围,也为降低汽车制动噪声提供了一种新的研究思路。
1 耦合仿真算法
离散元法将整个散体看作离散单元的组合,分为颗粒和块体两大系统,每个颗粒或块体为一个单元,根据单元间力的相互作用和牛顿运动定律描述散体群行为。其运算法则是以运动方程的有限差分为基础,以颗粒间作用模型为理论核心。离散元法适合计算颗粒阻尼器中颗粒的运动特性,有限元法能满足带颗粒阻尼的复杂结构的响应分析。本文结合有限元法与离散元法的特点,提出了基于有限元-离散元的耦合仿真算法,应用DMAP语言对工程有限元软件NASTRAN进行二次开发,通过MATLAB将有限元法与离散元法进行耦合[10]。
1.1 接触力学模型
离散元法是模拟运动在颗粒中传播的过程。颗粒运动必然会导致颗粒间的相互碰撞,颗粒之间也必然有接触力产生。球状颗粒间产生接触力的条件是两球心之间的距离小于两球半径之和。两球状颗粒接触时的相对运动有三种:在连心线方向上的法向运动;在两接触面的相对切向运动;两球的相对转动。本文在分析颗粒间的接触特性时,只考虑法向和切向接触力作用。法向作用力为
(1)
带颗粒阻尼器结构在旋转运动时,颗粒除了受到颗粒间及颗粒与孔腔间的接触力外,还受到离心力作用。其离心力的大小为
P=mω2r
(2)
式中m为颗粒的质量,ω为结构的转速,γ为颗粒的离心半径。
1.2 颗粒接触时步
计算过程中,要保证颗粒加速度是近似恒定和在一个时步内每个颗粒的动量只能传播给其临近的颗粒。根据瑞利波沿着颗粒表面的传播速度得到临界时间步长为
(3)
式中G为剪切模量,ρ为颗粒密度,γ为泊松比,Rmin为颗粒最小半径。
根据瑞利波确定的时步一般能满足数值仿真收敛的要求。对于颗粒间相对速度很大的情况,当与一个颗粒接触的颗粒数大于等于4时,此时这个颗粒的接触时间取公式中的20%较为合适;当与一个颗粒接触的颗粒数小于4时,此时这个颗粒的接触时间取公式中的40%较为合适。事实上,尽管很多学者对合理时步的选取做了大量工作,但由于时步的选取与很多因素有关,因此在实际计算时还应结合实际情况通过试算来确定。
1.3 颗粒运动方程
通过离散元法对系统中每个颗粒进行运动学分析,分析每个颗粒对系统的作用力即可得到整个系统的受力特性,将颗粒对系统的作用力作为边界条件载入到有限元模型进行下一步分析。单个颗粒的受力由牛顿第二定律得到
(4)
式中xi(t)为平动位移,∑F(t)为合力,mi为质量,∑M(t)为合力矩,θi(t)为角位移,Ii为转动惯量。
由中心差分法可得中心时刻颗粒的速度和加速度
在诸城市南部山区的康岭山上,占地1.2万亩的榛子林让原本光秃秃的山头,如今变成了树的海洋。“俺每天都来转转,看着这些满山成片的绿色,人就变得更有干劲儿。”64岁的魏本欣是这一片榛子林的主人,他将周边村落的山岭薄地流转过来,荒山造林,还带动百姓脱贫致富。

(5)
(6)
这样,经过Δt时间后颗粒i移动到新位置,计算颗粒收到的新的合力∑F(t+Δt/2) 和合力矩∑M(t+Δt/2)后返回式(6)计算,对颗粒i循环计算即可得到其运动特性。
2 带颗粒阻尼的制动鼓振动特性
本节将通过有限元和离散元法研究制动鼓在强迫振动下的振动特性,首先用有限元计算一个步长内结构的响应,提取孔腔的位移;然后根据孔腔位移用离散元计算颗粒之间接触力及颗粒与孔壁之间的接触力、一个步长内颗粒的位移、速度和加速度;再将颗粒与孔壁之间的接触力作为边界条件载入到制动鼓的有限元模型,计算制动鼓的响应特性,提取孔腔新的位移,如此循环。其有限元模型如图1所示,制动鼓被划分为48 080个单元。制动鼓的尺寸为直径866 mm,高240 mm,壁厚16 mm。

图1 制动鼓的有限元模型
由于制动鼓的前两阶模态体现为制动鼓圆柱部分的振动。因此,为方便起见,仅在圆柱部分进行模态试验测试,制动鼓的密度为7 330 kg/m3,杨氏模量为115 GPa,泊松比为0.27。通过模态试验得到如图2,3所示的前两阶模态振型,试验模态频率与有限元计算频率如表1所示。试验结果与有限元计算结果对比,表明所建立的有限元模型是准确的。

表1 模态试验和有限元计算结果比较
表1中的误差计算公式为:误差=(计算结果-平均试验结果)/平均试验结果。
图2 第一阶试验模态振型(243 Hz)

图3 第二阶试验模态振型(628 Hz)
在制动鼓上打孔并填充颗粒进行试验测试。颗粒填充率分别为:0%,30%,50%,70%和90%;激振力幅值分别取:1,2,3和4 N;试验中第一、二阶激振力频率范围分别选取225~255 Hz和580~700 Hz(参考模态试验得到的无颗粒阻尼器时,制动鼓的前两阶固有频率)。试验测试如图4所示,沿制动鼓周缘等间距布置20个直径为8 mm、深度为90 mm孔腔,填充颗粒后,在第一、二阶共振频率附近以幅值为4 N的激振力激振。

图4 制动鼓振动测试系统
颗粒之间及颗粒与孔壁之间的弹性恢复系数都为0.78,填充颗粒为直径1 mm的钢球。图5,6分别为填充直径为1 mm钢球颗粒时拾振点的响应均方根值与激振频率的关系曲线,由这两幅图可得到各种颗粒填充率下制动鼓的第一、二阶共振频率;激振力频率为制动鼓第一、二阶共振频率时,各种激振力幅值下拾振点的响应与填充率的关系如图7,8所示。图中,Cal 表示仿真结果,Exp表示试验结果。从图5,6可以看出:在制动鼓发生一阶共振且其他参数相同时,颗粒填充率为70%左右的系统减振效果最好;在制动鼓发生二阶共振且其他参数相同时,颗粒填充率为90%左右的系统减振效果最好。这说明在设计颗粒阻尼器时,应要充分考虑需增加阻尼的阶次,否则难以达到最佳减振效果。
从图7可以看出:当颗粒填充率为70%,在不同幅值的正弦激振力作用下,制动鼓发生一阶共振时,系统都达到最好的减振效果;激振力幅值为1,2,3,4 N时,对应的制动鼓响应均方根值最大降低了52%,61%,62%,62%,说明在共振频率处颗粒阻尼器能有效地降低制动鼓响应。
从图8可以看出:当颗粒填充率为90%,在不同的正弦激振力作用下,制动鼓发生二阶共振时,系统达到最好的减振效果。通过与图7,8的比较可以发现颗粒填充率对制动鼓不同阶次共振条件下减振效果的影响规律是不同的,因此在设计颗粒阻尼器时,应根据需要重点减振的频带范围来确定合适的颗粒填充率。
从图5~8可以看出计算结果与试验结果具有很好的一致性,进一步证实了制动鼓有限元模型及仿真算法的正确性,鉴于此,下面将只通过数值仿真计算来研究制动鼓的响应均方根值与其他参数的关系。
填充颗粒直径为1 mm钢球,激振力幅值为1 N,调整激振力频率使制动鼓发生第一、二阶共振,此时制动鼓响应与孔径粒径比(孔腔直径与颗粒直径的比值)的关系如图9和图10所示。从图中可以看出:在其他参数相同的情况下,当制动鼓发生第一、二阶共振时,颗粒阻尼器的减振效果在孔径粒径比8左右时,系统达到了最佳的减振效果。设计颗粒阻尼器孔径粒径比时,要考虑可能存在的最优值。
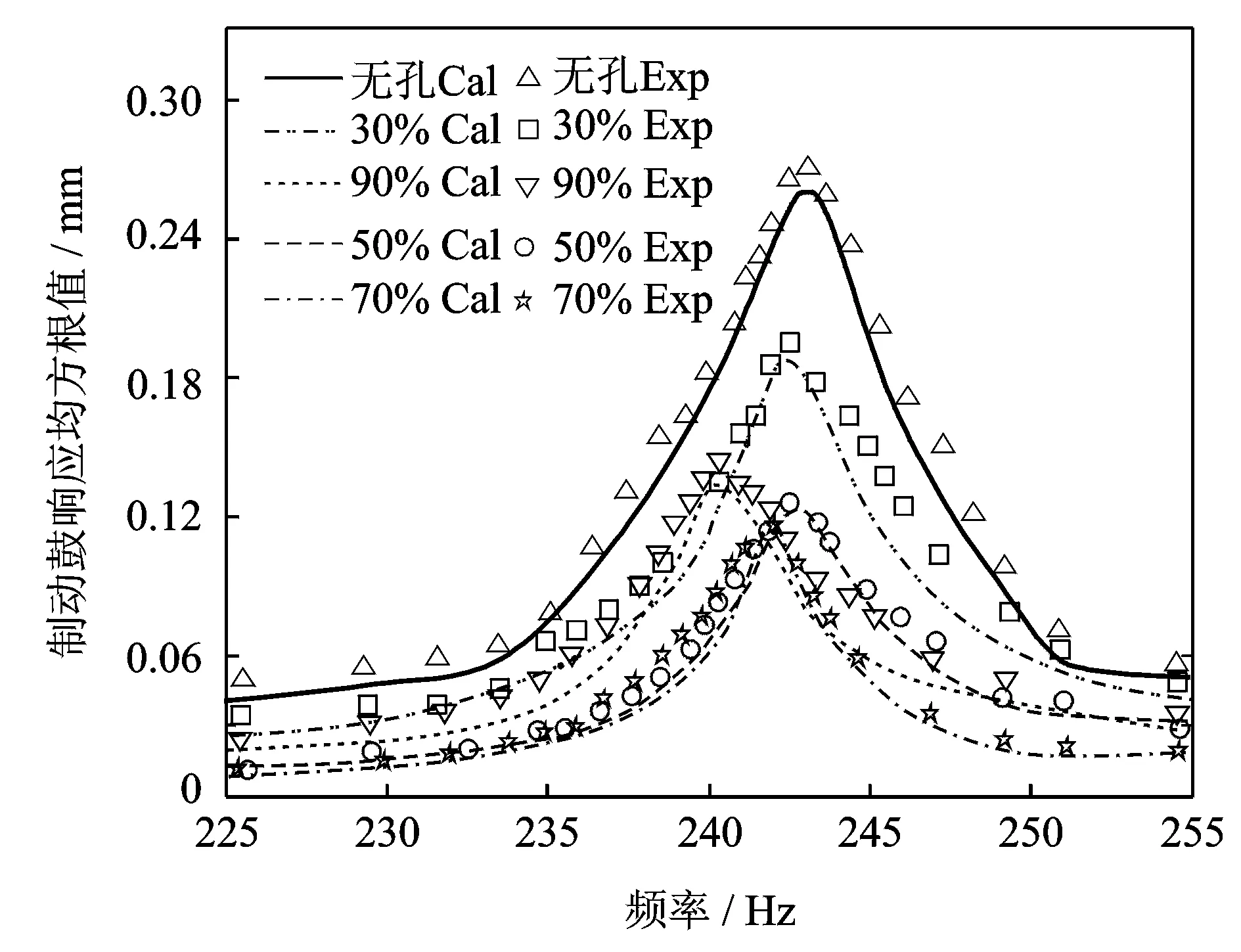
图5 制动鼓仿真与实验结果比较图(第一阶共振)

图6 制动鼓仿真与实验结果比较图(第二阶共振)
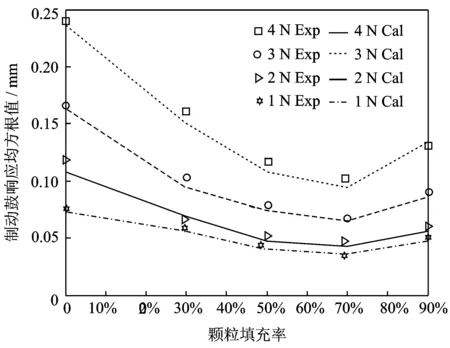
图7 制动鼓响应与填充率的关系(第一阶共振)

图8 制动鼓响应与填充率的关系(第二阶共振)

图9 制动鼓响应与孔径颗径比的关系(第一阶共振)
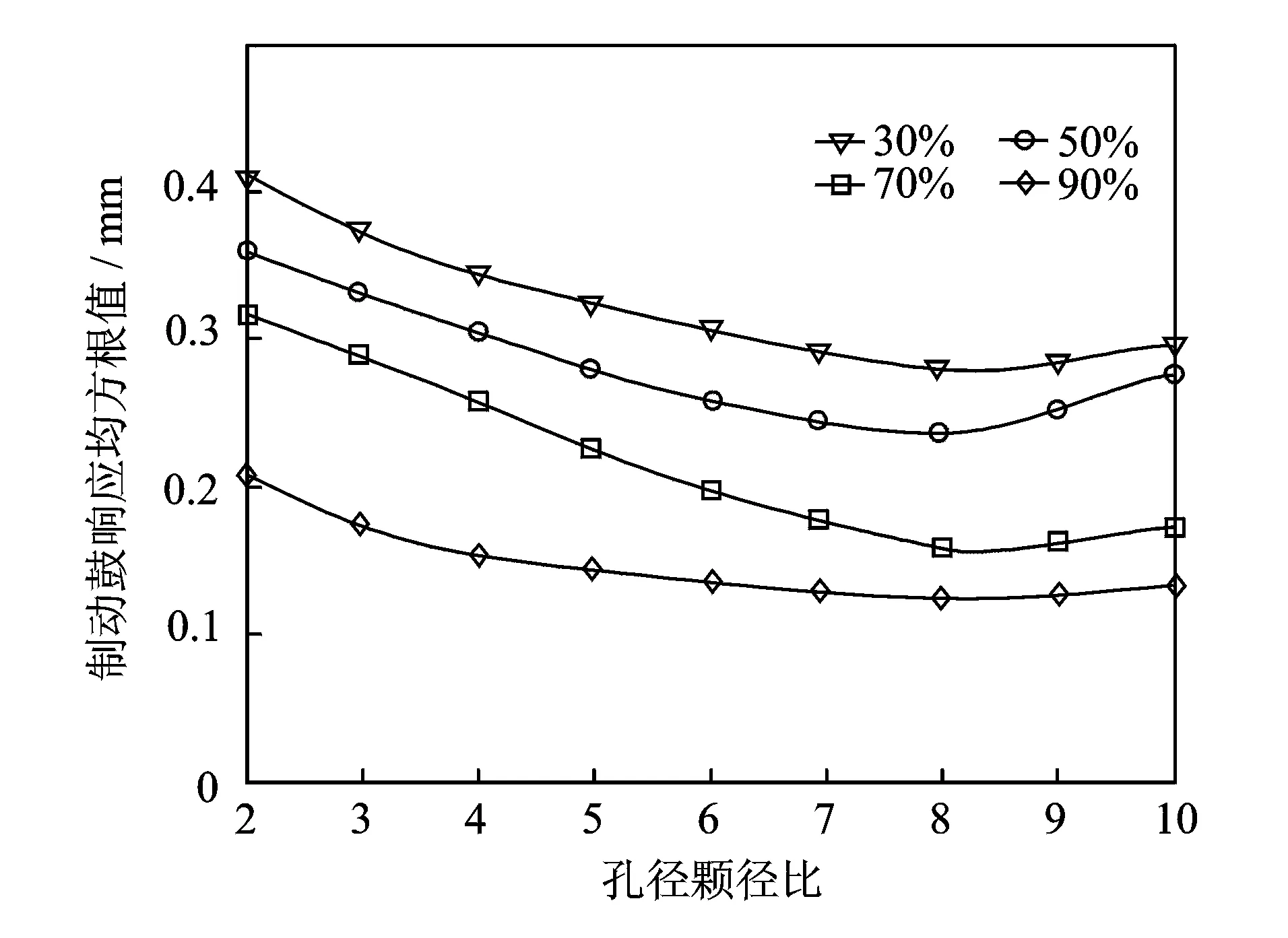
图10 制动鼓响应与孔径颗径比的关系(第二阶共振)
下面仿真分析制动鼓在旋转状态下颗粒阻尼与孔腔数的关系:
填充颗粒直径为1 mm钢球,激振力幅值为1 N,调整激振力频率使制动鼓发生第一、二阶共振,此时制动鼓的响应与孔腔数量的关系如图11和图12所示。从图中可以看出:在其他参数相同的情况下,当制动鼓发生第一、二阶共振时,颗粒阻尼器的减振效果都是随着孔腔数量增加而更明显。说明在汽车制动鼓上施加颗粒阻尼器时,应该在满足刚度和强度的条件下尽可能的增加孔腔数量。

图11 制动鼓响应与孔腔数量的关系(第一阶共振)
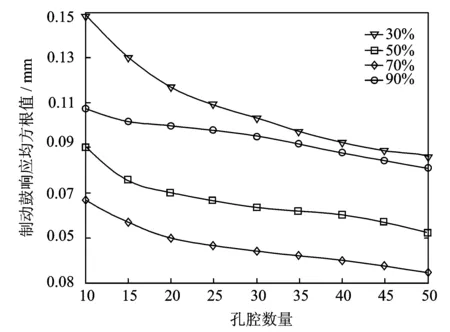
图12 制动鼓响应与孔腔数量的关系(第二阶共振)
孔腔直径为8 mm、深度为90 mm、数量为20个,颗粒填充率为70%,填充颗粒为直径1 mm钢球,正弦激振力幅值为4 N,调整激振力频率使制动鼓发生共振,研究此时各种孔腔数量下制动鼓响应随转速的变化规律。设制动鼓转速范围为0~500 r/min,由于旋转制动鼓结构的共振频率随转速改变而改变,激振力频率分别为各转速下的第一阶、二阶共振频率。旋转制动鼓在激振力作用下的响应曲线分别如图13和图14所示。制动鼓共振频率和转速的关系如图15所示。从图13和图14可以看出:不同数量的颗粒阻尼器对各阶振动的抑制规律基本一致,即在转速较低时抑制效果好,随着转速提高,抑制效果逐渐减弱,在制动鼓转速达到100 r/min时,颗粒阻尼仍有明显的减振效果,随转速提高,减振效果趋于稳定;制动鼓第一、二阶响应在转速较低时较小,但随着转速增加而增加,在转速达到一定值时转速对响应的影响趋于稳定。其原因是:在转速低时颗粒受到的离心力小,颗粒能充分发挥摩擦和碰撞,以此来消耗制动鼓的能量,随着转速的提高,由于离心力变大,颗粒之间的压紧力增加,因而颗粒之间的约束增加,因此在耗能机制中碰撞耗能大幅减少,颗粒阻尼表现出的阻尼减少,振动响应变大;在转速达到一定值时,颗粒在较大离心力作用下变得不活跃,颗粒间、颗粒与孔壁间几乎无碰撞,颗粒与旋转制动鼓的相对速度小,当结构在激励下发生弹性变形时颗粒在孔壁的推动下颗粒间、颗粒与孔壁间发生位移和摩擦,因此仍表现出比结构本身较大的阻尼。

图13 制动鼓旋转状态下响应与转速的关系(第一阶)
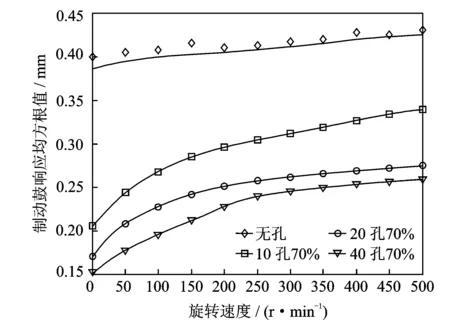
图14 制动鼓旋转状态下响应与转速的关系(第二阶)

图15 制动鼓第一、二阶共振频率与转速之间的关系
3 结 论
本文采用基于离散元和有限元法的耦合仿真算法研究了带颗粒阻尼器的制动鼓结构的动力学特性,计算了简谐激振下制动鼓的稳态响应,分析了制动鼓旋转状态的振动特性。通过上述研究得到的主要结论如下:
(1) 在制动鼓发生一阶共振且其他参数相同时,颗粒填充率为70%左右的系统减振效果最好;在制动鼓发生二阶共振且其他参数相同时,颗粒填充率为90%左右的系统减振效果最好。这说明在设计颗粒阻尼器时,应根据结构需要减振的频带确定合适的填充率。
(2) 在其他参数相同的情况下,当制动鼓发生第一、二阶共振时,颗粒阻尼器的减振效果在孔径粒径比为8左右时,系统达到了最佳的减振效果。说明颗粒阻尼的孔径粒径比存在的最优值。
(3) 颗粒阻尼器的减振效果随孔腔数量增加而更明显。在设计颗粒阻尼器时,应该在满足刚度和强度的条件下尽可能的增加孔腔数量。
(4) 在制动鼓转速较低时颗粒阻尼器的减振效果较好,随着转速提高抑制效果逐渐减弱,在转速达到100 r/min时,颗粒阻尼仍有明显的减振效果,随转速提高减振效果趋于稳定。
参考文献:
[1] Steven E O. An analytical particle damping model [J]. Journal of Sound and Vibration, 2003, 26:1 155—1 166.
[2] Xia Zhaowang, Liu Xiandong, Shan Yingchun. Coupling simulation algorithm of discrete element method and finite element method for particle damper [J]. Journal of Low Frequency Noise, Vibration and Active Control, 2009, 28(3):197—204.
[3] Zheng Lu, Xilin Lu, Masri S F. Studies of the performance of particle dampers under dynamic loads [J]. Journal of Sound and Vibration, 2010,329:5 415—5 433.
[4] 段勇,陈前.软内壁颗粒阻尼器阻尼特性试验研究[J].振动工程学报,2011,24(2):215—220.Duan Yong, Chen Qian. Experimental investigation of damping properties of the parti-cle dampers with soft lining[J].Journal of Vibration Engineering,2011,24(2):215—220.
[5] 王炜,黄协清,陈天宁,等. 内蕴时间理论用于NOPD板结构响应计算的研究[J].振动工程学报,2003,24(1):127—132.Wang Wei, Huang Xieqing, Chen Tianning, et al. Response calculation of plates with non-obstructive particle damping using endochronic theory [J].Journal of Vibration Engineering,2003,24(1):127—132.
[6] Panossian H V. Structural damping enhancement via non-obstructive particle damping technique[J]. ASME Journal of Vibration and Acoustics, 1992,114(1):101—105.
[7] Wong C X, Rongong J A. Micro-model characterisation and application of particle dampers to vibrating structures [A]. 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Confer[C]. Newport, Rhode Island, 2006: 211—224.
[8] K Mao, M Wang, H Ding, et al. Simulation and characterization of particle damping in transient vibrations[J]. Journal of Vibration and Acoustics, 2004,126 (2):202—211.
[9] Papalou A, Masri S F. An experimental investigation of particle damper under harmonic excitation[J]. Journal of Vibration and Control, 1998,4(4):361—379.
[10] 夏兆旺,温华兵,刘献栋. 颗粒阻尼器结构振动特性耦合算法仿真与试验[J].农业机械学报,2011,42(8):26—29.Xia Zhaowang, Wen Huabing, Liu Xiandong. Coupling algorithm simulation and experiment of structure vibration characteristics for particle dampers[J].Transactions of the Chinese Society for Agricultural Machinery,2011,42(8):26—29.

