平压单瓦钙塑瓦楞纸板本构模型

高 德， 冯 军， 卢富德， 王剑平

(1.浙江大学生物系统工程与食品科学学院，浙江 杭州 310029；2.浙江大学宁波理工学院，浙江 宁波 315100)

引 言

钙塑瓦楞纸板是新型的包装材料，它是用钙塑瓦楞代替原牛皮纸瓦楞而得到的钙塑瓦楞纸板，与传统瓦楞纸板相比，具有如下优点:防水、防潮、高强度、质轻耐用、尺寸稳定、机械力学性能好等，可广泛用于商品的运输及储藏包装中。对于瓦楞纸板材料缓冲性能及其本构模型的研究，国内外学者主要研究工作有：1995年开始，Naganathan研究了瓦楞纸板尺寸、瓦楞纸板的内部气体对多块瓦楞纸板串联缓冲性能的影响[1，2]，瓦楞纸板在受到冲击时，瓦楞内部的气体对瓦楞纸板有作用，瓦楞纸板的尺寸大小对瓦楞纸板的动态缓冲性能影响大，但对静态性能没有显著影响。2001年高德对单块瓦楞纸板动态缓冲性能进行建模[3]，得到了应力是应变、应变率、跌落次数、湿度等参数的函数关系，使得瓦楞纸板作为缓冲结构的多自由度物品包装结构优化设计计算成为可能。2005年Sek和2007年Rouillard研究预压瓦楞纸板与未预压瓦楞纸板所组成的复合缓冲结构的力学性能[4，5]，当此结构遇到较小冲击时，预压瓦楞纸板以弹性变形来吸收外界能量，未经预压的瓦楞纸板没有达到其塑性变形；当遇到大的变形时，未预压的瓦楞纸板以塑性变形来吸收能量，此复合瓦楞结构充分运用预压瓦楞纸板在冲击小时的耗散能量优势，未预压瓦楞纸板在遇到大的冲击载荷会发生较大变形吸收外界能量。因此瓦楞纸板能有较强的应用范围，可替代塑料泡沫成为绿色缓冲包装材料。2009年Garcia-Romeu-Martinez研究瓦楞纸板材料在多次连续冲击下缓冲性能的影响[6]，当瓦楞纸板预压95%，连续跌落35次，第一次与最后一次的最大加速度仅相差20%，这明显比其他缓冲材料好。2012年卢富德等在给定单块瓦楞纸板本构关系的基础上[7～10]，用虚拟质量法分析多块瓦楞纸板串联情形下的准静态和动态压缩响应，与瓦楞纸箱的实际使用状况更接近。而对于钙塑瓦楞纸板材料的性能方面的研究，未见报导。

以上文献所得到的成果虽然为瓦楞纸板的应用及开发提供了指导，但钙塑瓦楞板是纸-钙塑复合而成，属于新型瓦楞纸板的一种。为进一步开发钙塑瓦楞纸板及其产业化，需要定量了解其静态、动态本构关系，为此本文采用气动垂直冲击试验台测试瓦楞板的动态性能，建立动态本构模型，为钙塑瓦楞纸板的运用奠定基础。

1 试验材料与设备

1.1 材料

本文研究的钙塑瓦楞复合纸板，它是由一层钙塑瓦楞芯材和牛皮面面纸及牛皮里纸里层复合而成，如图1所示。牛皮面纸和里纸的定量为200 g/m2，钙塑片材定量为328 g/m2，此钙塑瓦楞复合纸板的总定量为728 g/m2，厚度为5 mm。

图1 钙塑瓦楞纸板图形

1.2 主要仪器设备

准静态压缩试验测试的仪器主要设备是CMT6103型微机控制电子万能试验机，新三思集团公司。动态压缩试验在SY11-100气压驱动垂直冲击试验台(东菱振动试验仪器有限公司)上进行，测试设备结构如图2。

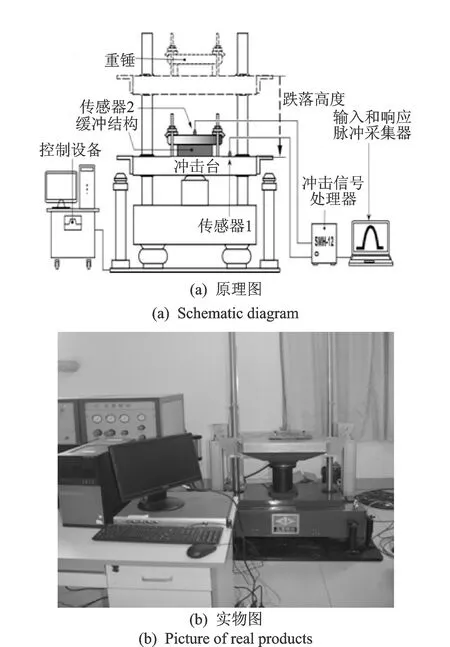
图2 垂直冲击试验台

2 钙塑瓦楞纸板的静态和动态压缩试验及其模型

2.1 钙塑瓦楞纸板静态平压试验

钙塑瓦楞纸板试件的楞型为C型，厚度为5 mm，面积为64.5 cm2,按照ISO2233-1972标准进行处理，测试环境条件为23oC、相对湿度为50%。平压速度为2 mm/min,直至试样压溃,试验重复5次，得到静态压缩应力-应变曲线如图3所示。

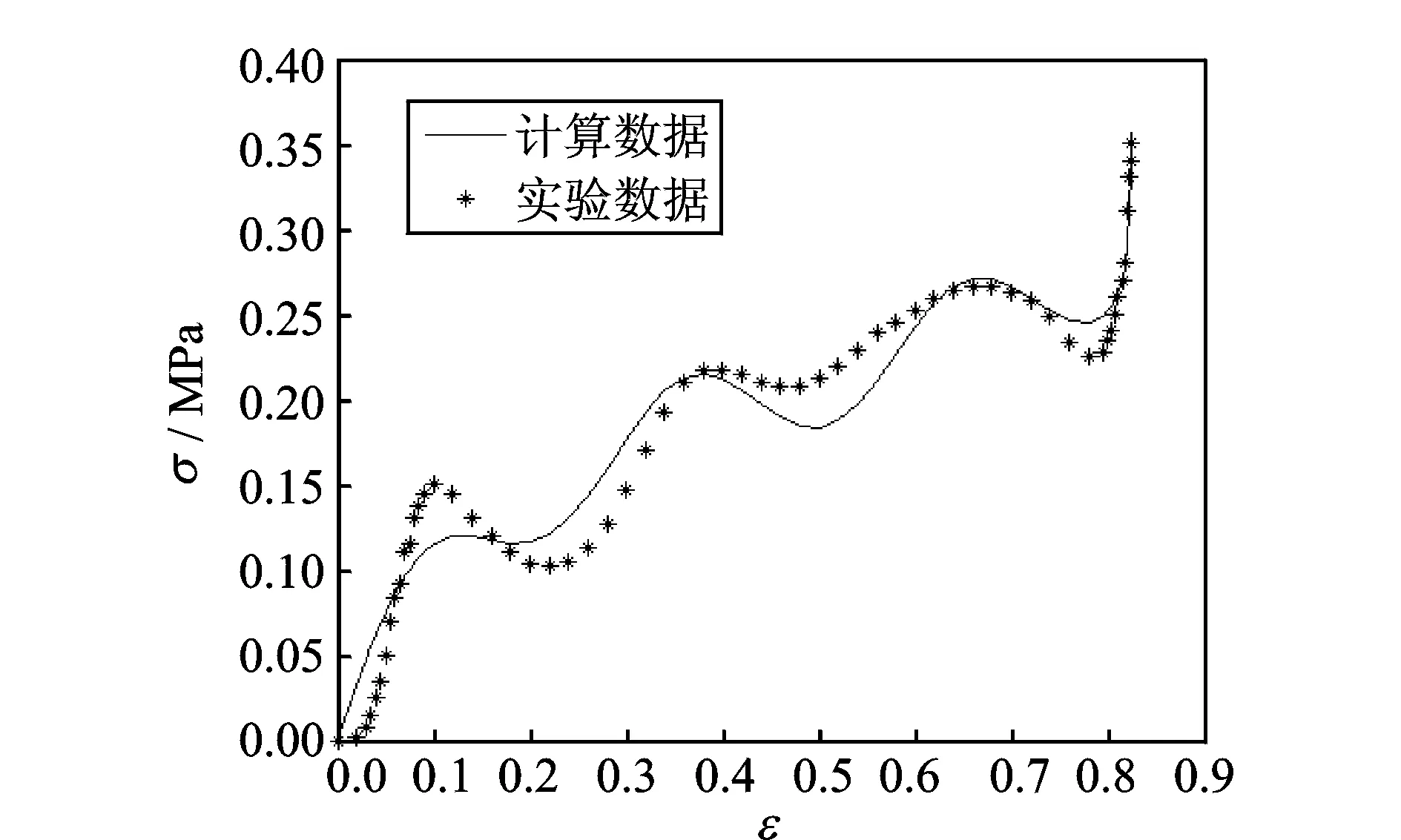
图3 钙塑瓦楞复合纸板静态应力-应变曲线理论值与试验值

由图3表明，钙塑瓦楞纸板应力-应变曲线呈现波动上升趋势，应变小于0.1时，呈线性关系；应变大于0.1且小于0.8，呈现波浪式上升行为，这一阶段是瓦楞结构用于吸收能量的主要阶段；应变大于0.8，伴随材料的压实过程，应力急剧上升。参考文献[7,11],本文提出钙塑瓦楞纸板静态平压模型

σ=a1ε+a2sin(a3ε)+a4tanh(a5ε)+a6tan(a7ε)

(1)

式中a1～a7为待识别参数。第2项的正弦函数用于表征应力-应变曲线的波动行为。第3项双曲正切函数用于表征应力-应变曲线的塑性阶段，第1项线性函数表示塑性阶段线性增加，这两项共同表征塑性阶段的线性增加行为；由此前三项之和得到波浪式上升的屈服阶段。另外双曲正切函数的原点的导数项代表钙塑瓦楞纸板的初始线性行为，公式(1)的最后一项正切函数项，其模拟瓦楞结构压缩特性，但此函数并不影响结构的线弹性、波浪式上升区域。因此，这四项的综合运用，可以用来表达钙塑瓦楞纸板在压缩载荷下所表现的线弹性、波浪式上升和压实过程等3个典型阶段。

根据式(1)的钙塑瓦楞纸板静态压缩模型，应用高斯-牛顿法识别其中的参数a1～a7，识别的结果如表1。

表1 钙塑瓦楞纸板静态压缩模型参数识别结果

将识别的结果代入式(1)中，得到钙塑瓦楞复合纸板的拟合曲线，如图3中的实线所示。试验值与理论值平均相对误差为4.86%，满足工程需要。

2.2 钙塑瓦楞复合纸板动态压缩测试

2.2.1 测试原理

材料动态测试原理示意图如图4所示，质量块m与钙塑瓦楞纸板放在冲击台面上，在冲击台面M上加载半正弦脉冲激励如下[12]：

(2)

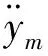
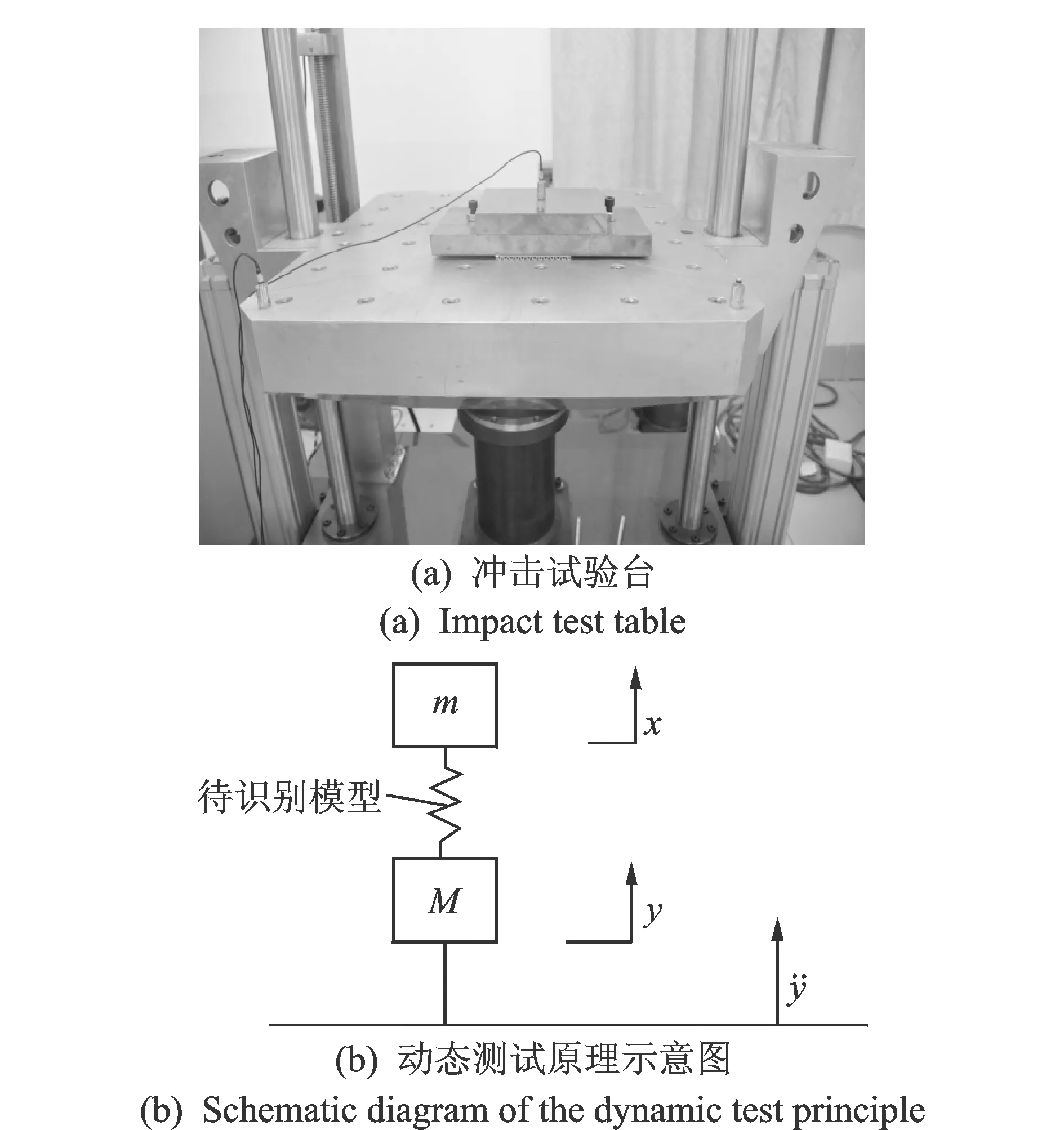
图4 动态测试原理

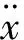
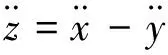
(3)

式(3)经过两次积分，即可得到钙塑瓦楞纸板的变形为

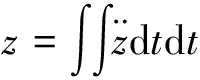
(4)

因此得到钙塑瓦楞纸板的名义应变为

(5)

则钙塑瓦楞纸板的应力为

(6)

式中A为钙塑瓦楞纸板试样的面积。

2.2.2 测试结果

动态压缩试验在SY11-100气压驱动垂直冲击试验台上进行。试样尺寸为100 mm×100 mm，厚度为5 mm。依据GB/T4857.2-1992要求进行预处理，重锤的质量为3 kg，跌落高度H=0.3 m。由冲击试验台，测得输入与输出加速度信号如图5所示，进而得到相对压缩速度、相对压缩位移如图6，7。应变率-时间曲线和应力-时间曲线，如图8(a)和(b)所示。

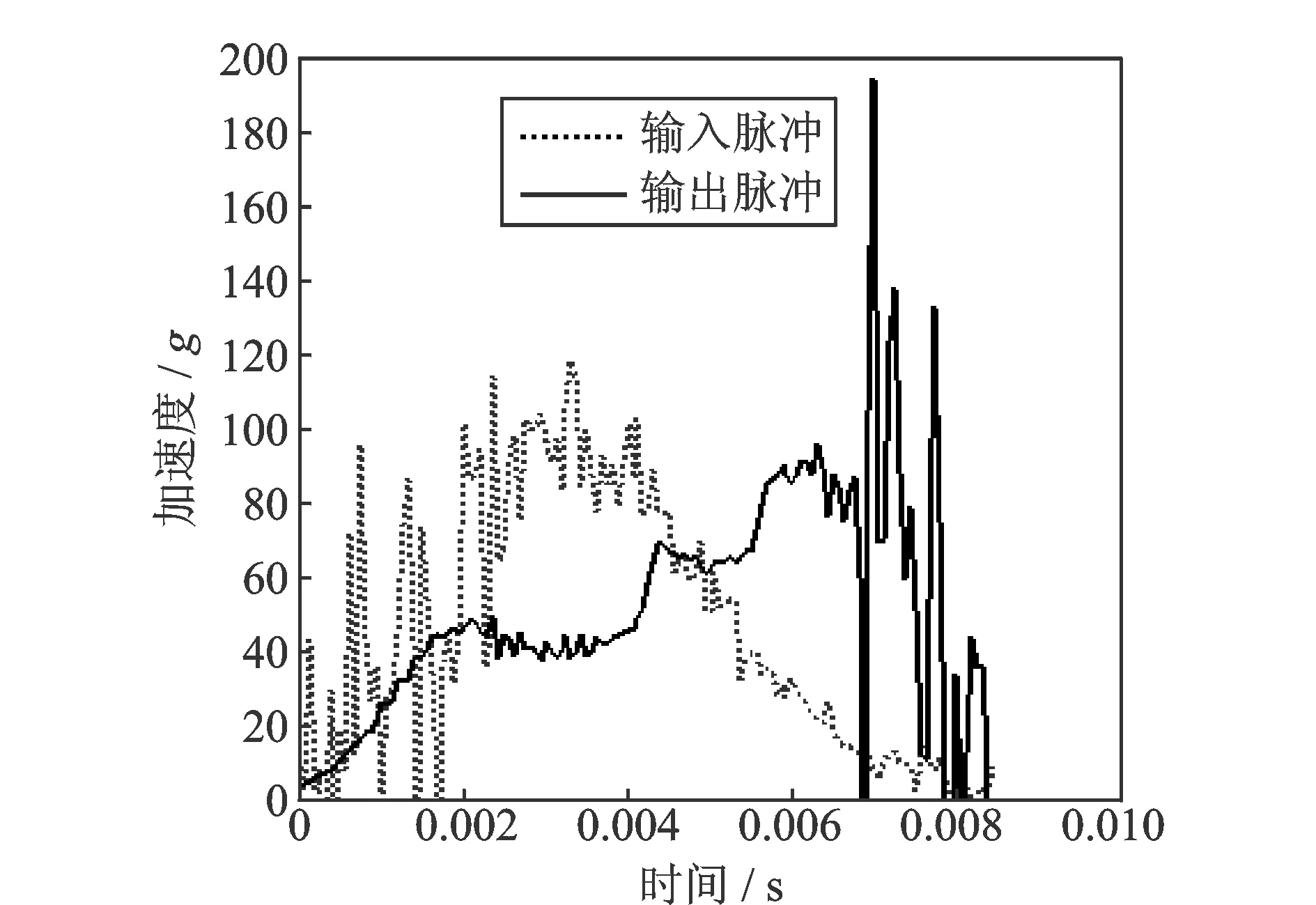
图5 输入输出信号

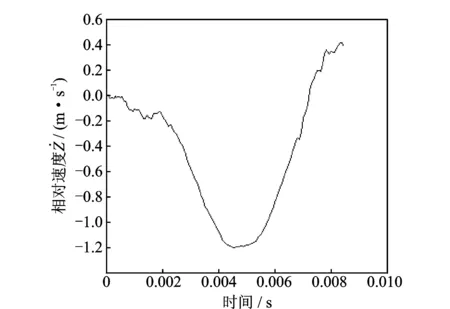
图6 相对压缩速度与时间的关系

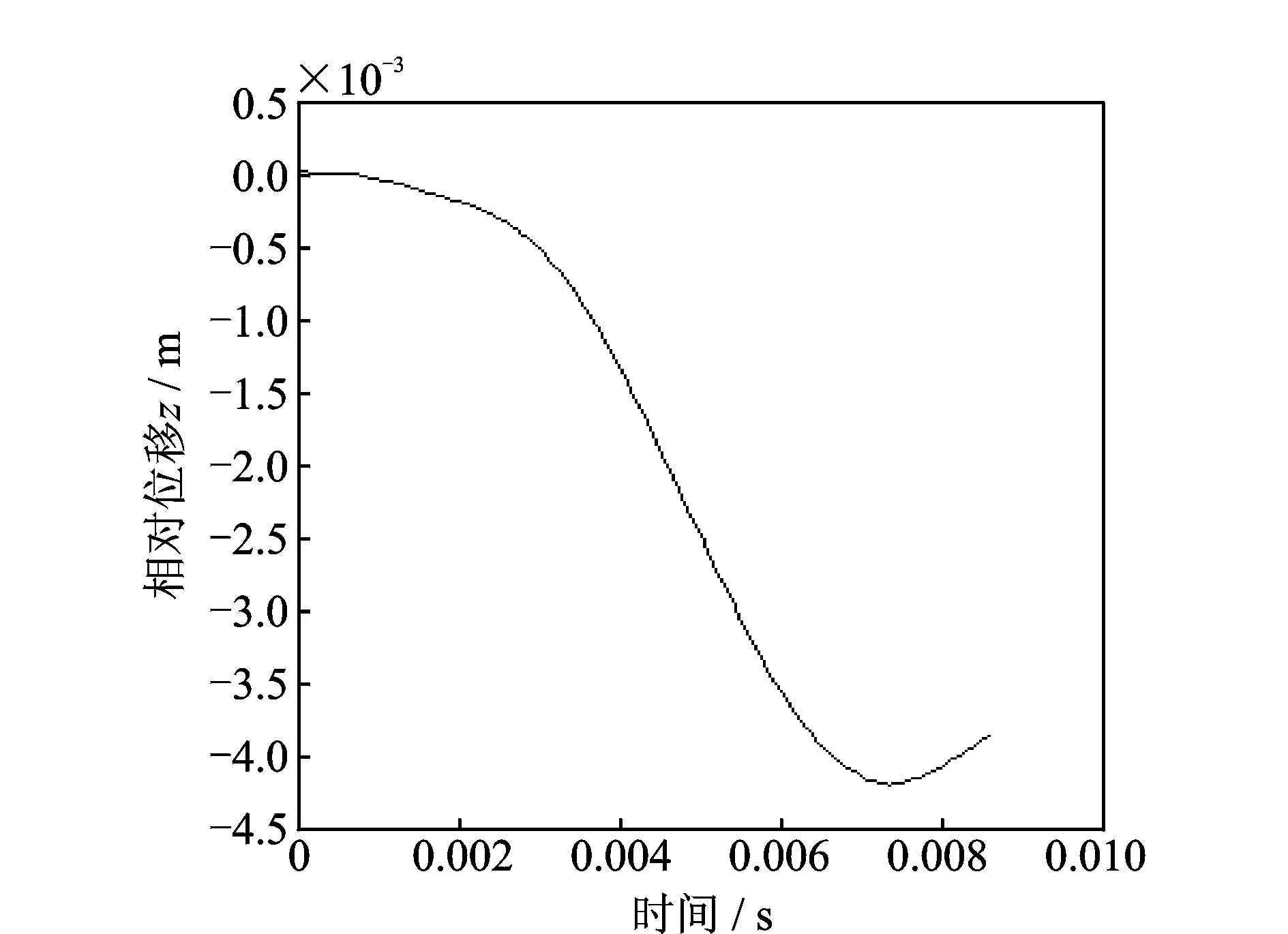
图7 相对位移与时间的关系

图8 应变率、应力-时间曲线

2.3 动态模型建立及结果分析

图8(a)和(b)所示的Q到R阶段，钙塑瓦楞纸板处于塑性阶段，其应变率位于35.6～238/s,而瓦楞纸板在准静态压缩应变率为0.006 67/s，二者相差几万倍。

联立式(5)，(6)即可得到动态应力与应变的关系如图9中的实线所示。

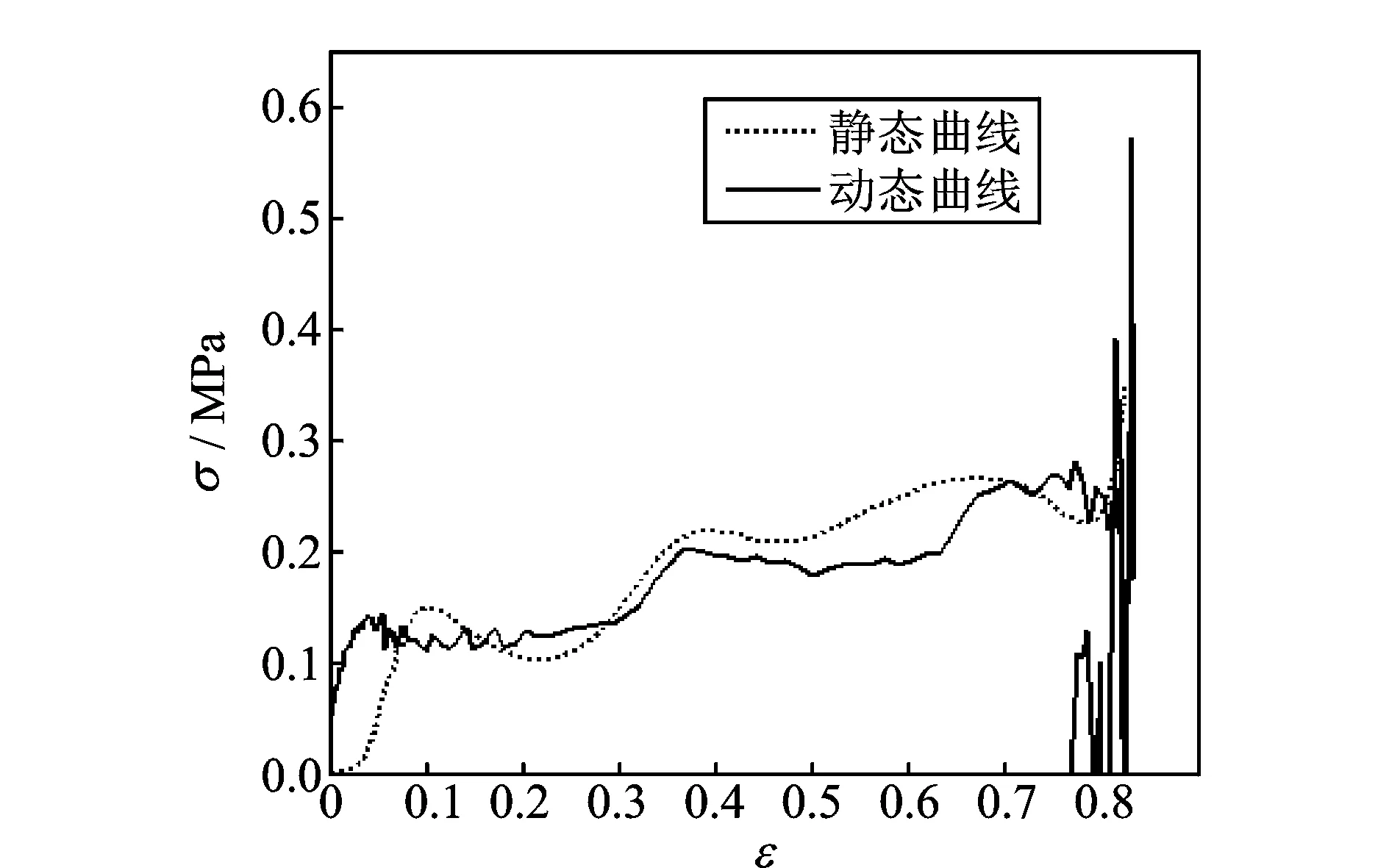
图9 静态与动态应力-应变曲线的对比

由图9可以得到，钙塑瓦楞复合纸板的动态应力-应变曲线与静态应力-应变曲线基本形状相似，平均屈服应力几乎相等，说明此钙塑瓦楞纸板对应变率不敏感。还可以得出，瓦楞纸板在准静态与动态载荷下的弹性模量存在相位差，比较符合非线性粘弹塑性模型的特征。

依据静态测试及动态测试结果，利用非线性粘弹塑性模型原理，建立钙塑瓦楞纸板的动态本构模型如下式

(7)

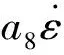
表2 动态本构模型参数识别结果

将识别的结果代入式(7)中，得到理论结果与测试曲线对比图如图10所示。

理论值与试验值平均相对误差为6.2%，所得出的本构关系可以直接应用于考虑钙塑瓦楞复合纸板箱缓冲作用的产品跌落冲击响应与优化设计[13～15]。

图10 钙塑瓦楞复合纸板动态试验理论结论与测试结果

3 小 结

通过静、动态压缩试验，得到钙塑瓦楞复合纸板的静态压缩的实验曲线建立了钙塑瓦楞复合纸板的静态压缩模型，瓦楞纸板呈现线弹性、波动式上升塑性屈服和压实区域，根据此力学特点，得到钙塑瓦楞纸板非线性本构关系。利用脉冲激励的方法，对钙塑瓦楞复合纸板进行动态压缩试验，进而建立其动态压缩模型。通过对比静态、动态试验数据，钙塑瓦楞复合纸板率不相关，静态、动态载荷作用下的瓦楞纸板弹性模量存在相位差，从而得到瓦楞纸板非线性的本构关系。得出的钙塑瓦楞纸板本构关系可以直接应用于考虑钙塑瓦楞复合纸板箱缓冲作用的产品跌落冲击响应与优化设计。瓦楞纸板上下面的最大相对压缩速度为1.19 m/s时,其压缩应变率高达238/s,而瓦楞纸板在准静态压缩应变率为0.006 67/s，二者相差几万倍，但从图8得到，平均屈服应力几乎相等，说明此新型瓦楞纸板应变率不相关性，这是由于钙塑瓦楞的材料性能决定的。

参考文献：

[1] Naganathan P B, Marcondes J A. Effect of specimen size on test results to determine cushioning characteristics of corrugated fibreboard[J].Packaging Technology and Science, 1995,8(2):85—95.

[2] Naganathan P B, He J, Kirkpatrick J. The effect of compression of enclosed air on the cushioning properties of corrugated fibreboard[J]. Packaging Technology and Science,1999,12(2)：81—91.

[3] 高德,王振林,陈乃立,等.B楞双层瓦楞纸板衬垫平压缓冲动态性能建模[J].振动工程学报，2001，14(2)：172—177.Gao De,Wang Zhen-lin,Chen Nai-li,et al.The dynamic modeling of flat compression cushion made up of B-flute double-wall corrugated fibreboard[J].Journal of Vibration Engineering, 2001，14(2)：172—177.

[4] Sek M, Rouillard V, Tarash H, et al. Enhancement of cushioning performance with paperboard crumple inserts[J]. Packaging Technology and Science,2005,18(5):273—278.

[5] Rouillard V, Sek M A. Behaviour of multi-layered corrugated paperboard cushioning systems under impact loads[J]. Strain,2007,43(4):345—347.

[6] Garcia-Romeu-Martinez M A, Sek M A, Cloguell-B allester V A, et al. Effect of initial pre-compression of corrugated paperboard cushions on shock attenuation characteristics in repetitive impacts [J]. Packaging Technology and Science,2009,22(6):323—334.

[7] 卢富德,高德.C楞瓦楞纸板动态缓冲模型及应用[J].功能材料,2012,43(1):39—41.Lu F D, Gao D. Cushion model and its application of C-flute corrugated paperboard[J]. Journal of Functional Materials, 2012,43(1)：39—41.

[8] 卢富德，陶伟明，高德.瓦楞纸板串联缓冲系统动力学响应[J].振动与冲击，2012，31(21):30—32.Lu F D,Tao W M, Gao D. Dynamic response of a series cushioning packaging system made of multi-layer corrugated paperboard[J].Journal of Vibration and Shock, 2012，31(21):30—32.

[9] 卢富德，陶伟明，高德.串联缓冲结构压缩响应虚拟质量分析[J].浙江大学学报(工学版)，2012,46(8):1 431—1 436.Lu F D,Tao W M, Gao D.Compression responses of series cushioning structures by a virtual mass method[J].Journal of Zhejiang University(Engineering Science), 2012,46(8):1 431—1 436.

[10] LU F D,TAO W M,GAO D.Virtual mass method for solution of dynamic response of composite cushion packaging system[J].Packaging Technology and Science,2013,26(S1):32—42.

[11] 高德，卢富德.考虑转动的双曲正切与正切组合模型缓冲系统冲击响应研究[J]. 振动工程学报，2012,25(1)： 6—11.Gao D, Lu F D. The shock response of hyperbolic tangent and tangent comprehensive model on cushion system considering rotary motion[J]. Journal of Vibration Engineering, 2012,25(1)： 6—11.

[12] Zhong C, Saito K, Kawaguchi K. Improvement of equivalent drop theory for transport packaging[J]. Packaging Technology and Science ,2012, 26(2):67—81.

[13] 卢富德，高德.考虑蜂窝纸板箱缓冲作用的产品包装系统跌落冲击研究[J].振动工程学报，2012,25(3)：335—341.Lu F D, Gao D.Study on drop impact of packaging system considering the cushioning action of honeycomb paperboard box[J].Journal of Vibration Engineering,2012,25(3)：335—341.

[14] 卢富德，陶伟明，高德. 串联缓冲系统冲击响应与结构优化分析[J].浙江大学学报(工学版),2012,46(10):1 773—1 777,1 789.Lu F D,Tao W M, Gao D. Impact response of series cushioning system and structure optimization analysis[J]. Journal of Zhejiang University(Engineering Science),2012,46(10):1 773—1 777,1 789.

[15] Gao D, Lu F D. Nonlinear dynamic analysis of series cushioning system made with expanded polyethylene and corrugated paperboard[J].Advances in Mechanical Engineering,2013, Article(376098):1—5.