基于多频外差原理的相位校正及匹配方法研究

黄亚楠，娄小平

(1.北京信息科技大学 光电测试技术北京市重点实验室，北京 100192；2. 北京信息科技大学 光电信息与仪器北京市工程技术研究中心，北京 100192)

引言

基于结构光的三维测量技术具有精度高、速度快等优点，广泛应用在航天航空、逆向工程等各个领域[1]。实际测量中，由于测量环境、物体表面特性等随机噪声的影响，采用实际采集的光栅图像求解的相位图存在较大噪声，出现相位值跳跃的不连续点。其次匹配是立体视觉中最重要的环节，通过将相位值作为匹配的一个特征向量，并结合极线约束实现匹配。相位跳跃会直接影响匹配的精度，最终导致三维重建点云的坐标误差很大。

本文提出一种相位校正方法，并比较相位校正对匹配的影响；其次利用校正后的相位值作为匹配的依据，采用极线对上基于相位的亚像素匹配方法，得到被测物表面的三维点云坐标。

1 基本原理

1.1 相移法

相移法利用多幅正弦光栅图像求解相位主值[2-3]。最广泛的方法是四步相移法，具有消除检测器偶次谐波(含常数项)影响的优点[4]。采用四步相移法得到包裹相位值的表达式为

(1)

φ(x,y)被反正切函数截断在[-π,π]内，在整个测量空间不连续。因此，必须对相位主值进行相位展开。

1.2 多频外差合成

多频外差合成是将两种不同频率的相位函数φ1(x)和φ2(x)，合成得到一种频率更低的相位函数Φ(x)[5]，如图1所示，λ1、λ2、λ12分别为相位函数φ1(x)、φ2(x)、Φ(x)的频率。其中λ12可表示为：λ12=|λ1λ2/(λ1-λ2)|。

图1 多频外差合成示意图Fig.1 Schematic diagram of multi-frequency heterodyne synthesis

1.3 多频外差展开

多频外差展开[6-7]是以合成后在摄像机范围内形成一级条纹内的光栅图像为基础，对各个参数与外差合成的不同频率的相位函数进行相位展开。

图2 多频外差展开示意图 Fig.2 Schematic diagram of multi-frequency heterodyne unfolding

如图2所示，λ1、λ2、λ3、λ4分别是4幅光栅图像的频率，相位值分别为φ1(x,y)φ2(x,y)、φ3(x,y)、φ4(x,y)，合成后等效频率为λ12、λ34、λ1234，相位值分别为φ12(x,y)、φ34(x,y)、φ1234(x,y)。λ1234满足λ1234≥W[8](W=800)。因为Φ1234(x,y)=φ1234(x,y)，故可将其作为参考相位展开λ12和λ34的相位，相位展开式为

Φm(x,y)=φm(x，y)+2π×

(2)

式中，m=12,34。已知相位Φ12和Φ34，故可展开λ1、λ2、λ3、λ4的相位。立体匹配只需一个光栅的相位值和仅需求解任意一个频率光栅的相位值，以求解λ2的相位为例，其相位展开式为

Φ2(x,y)=φ2(x，y)+2π×

(3)

2 相位校正方法

若包裹相位图没有噪声，则展开相位图在全场范围内是连续的[9]。实际测量中，由于随机噪声的存在，得到的展开相位图存在相位跳跃的不连续点。若不进行相位校正，会导致错误匹配。

相位图中出现需要校正的情况具体如下：

1)Φ2(i,j)≠0&&Φ2(i,j+1)≠0&&abs(Φ2(i,j+1)-Φ2(i,j))>thresh,经实验分析相位值跳跃7×2π，因此为了排除相位值原本是正确的像素点，本文选择15。

2)Φ2(i,j)=0&&Φ2(i,j+1)≠0

3)Φ2(i,j)=0&&Φ2(i,j+1)=0

设相邻像素点的相位值之差的绝对值为k=abs(Φ2(i,j+n+1)-Φ2(i,j+n))，(n=-10…10)，相位校正方法描述如下：

(4)

对于情况1),逐点比较其相邻邻域各10个像素点的相位差，若k小于thresh,则该点是正确的点；若k大于thresh,则将Φ2(i,j+n+1)加减2π×round(k/2π)。对于后2种情况，分别比较其左右邻域各10个像素点的相位差，校正方法同上所述。至此，得到连续分布的相位图，可为下一步的匹配做基础。

3 极线对上基于相位的亚像素匹配

图像对中对应点的局部相位值是相等的[10]，因此采用相位信息作为匹配的基元。为了实现亚像素级别的匹配，提出极线对上基于相位的亚像素匹配算法。

图3 亚像素匹配方法示意图Fig.3 Schematic diagram of sub-pixel matching method

图3为左相机的图像坐标系，R为待匹配点在左图像中的匹配点，lpl为对应极线，点R1和R2位于极线lpl上，且位于R的左右两侧，点P1、P2、P3、P4为位于点R1和R2两侧的整像素点。利用4个整像素点的相位通过线性插值得到R1和R2处的相位值，再利用(5)式得到R的亚像素列坐标：

(5)

式中：XRl为点R的列坐标；XR1、XR2为点R1、R2的列坐标；fP为待匹配点的相位值；fP1、fP2为点R1和R2的相位值。将亚像素列坐标代入极线方程，即可得匹配点R亚像素行坐标：

YRl=kXR1+b

(6)

式中，k和b为极线方程的系数，经标定实验得到基本矩阵F，求解得对应的极线方程为y=0.008 2x+454.967 3，故k=0.008 2,b=454.967 3。

4 测量系统及实验结果

4.1 测量系统

测量系统组成：一个LG的HS120G-JE型数字投影仪，分辨率为800×600像素；2个DH-SV1420FM型号数字相机，分辨率均为1 344×1 024像素，镜头焦距为16 mm,以及PC机、三脚架。如图4所示。

图4 测量系统Fig.4 Measuring system

4.2 实验结果分析

实验对象为标准平面及扇叶。以对标准平面的两两对应匹配程度评价相位校正对匹配的影响；然后利用亚像素匹配算法进行匹配；最后，对扇叶进行三维测量。

1) 标准平面

投射16幅正弦光栅图像至平面表面，光栅节距分别为14、16、18、21(像素)，合成后频率λ12=112、λ34=126、λ1234=1 008。表1、2列出了对相位图进行校正的整像素匹配情况。由表1知，相位校正前，左图像匹配点的像素坐标与原始的像素坐标误差很大。由表2知，相位校正后，坐标误差在1个像素内，能够准确实现整像素匹配。表3列出2种匹配算法的比较。

表1 相位校正前Table 1 Before phase correction 像素

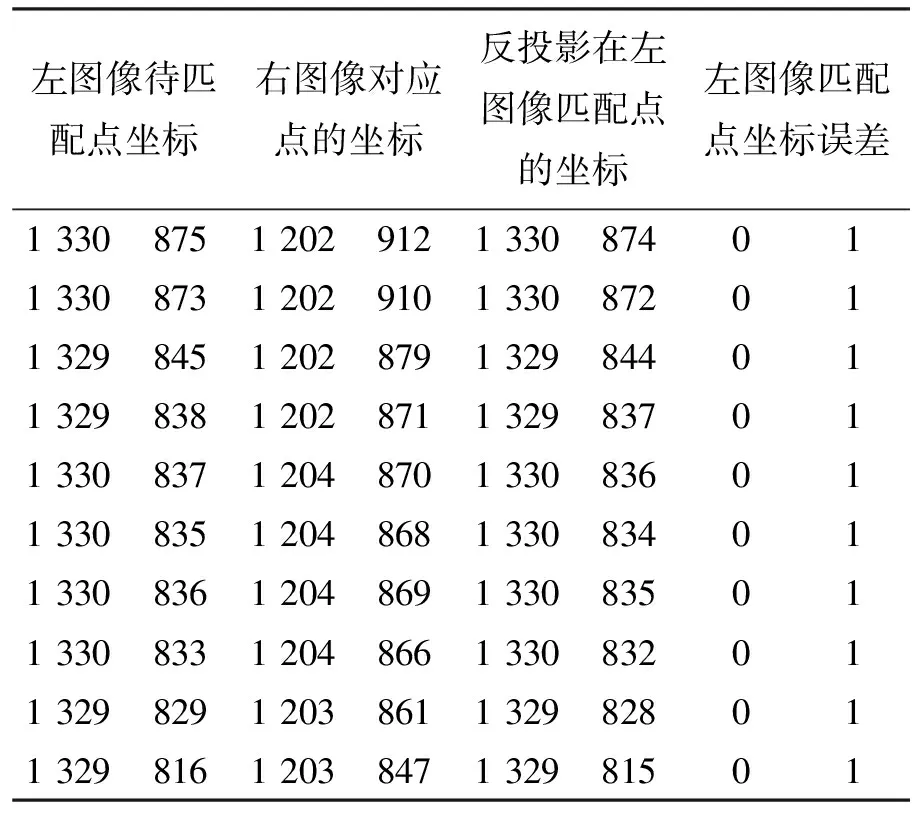
表2 相位校正后Table 2 After phase correction 像素

表3 两种算法的比较Table 3 Comparison of two algorithms 像素

2) 扇叶

对扇叶进行三维测量，图5为扇叶的相位解包裹示意图。

图5 λ12相位解包裹示意图Fig.5 Schematic diagram of phase unwrapping for λ12

图6为进行相位校正后的绝对相位高度图。首先利用λ1234的相位图Φ1234展开λ12的相位图Φ12;其次利用Φ12展开λ2的相位图Φ2。图6(a)为校正前λ2的绝对相位高度图;图6(b)为校正后λ2的绝对相位高度图。

图6 绝对相位高度图Fig.6 Absolute phase height maps

通过分析比较，图6(a)的高度图在扇叶的边缘处存在明显的水波纹且锐变较大；经相位校正后，图6(b)的高度图变得比较平滑，边缘处水波纹明显减小。

最后利用亚像素匹配方法，得到同名匹配点，再结合标定好的内外参数，完成三维点云的重建过程。扇叶的三维点云图如图7所示。

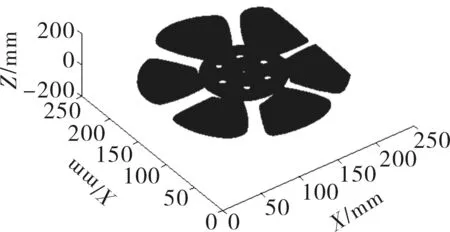
图7 扇叶三维点云图Fig.7 3D point cloud of flabellum

5 结论

该文提出一种相位校正方法，并比较相位校正前后的绝对相位高度图，表明该方法能够有效地校正相位误差；然后利用提出的亚像素匹配方法得到同名匹配点，最后利用立体视觉方法得到物体的三维点云数据。实验结果表明该方法能够应用在逆向工程、模具制造等各个领域，完成自由曲面的三维形貌测量。

[1] 陈晓荣, 蔡萍, 施文康. 光学非接触三维形貌测量技术新进展[J]. 光学精密工程, 2002, 10(5):528-532.

CHEN Xiao-rong, CAI Ping, SHI Wen-kang . New progress in non-contact optical measurement technology three-dimensional Morphology [J]. Optics and Precision Engineering, 2002, 10(5):528-532.(in Chinese with an English abstract)

[2] TOWERS C E, REID D T, MACPHERSON W N, et al. Fibre interferometer for multi-wavelength interferometry with a femtosecond laser [J]. Journal of Optics A: Pure and Applied Optics, 2005, 7(6): S415.

[3] YAMAGUCHI I, KATO J, MATSUZAKI H. Measurement of surface shape and deformation by phase-shifting image digital holography [J].Optical Engineering, 2003, 42(5): 1267-1271.

[4] 李中伟. 基于数字光栅投影的结构光三维测量技术与系统研究 [D]. 武汉: 华中科技大学, 2009.

LI Zhong-wei. Three-dimensional measurement techniques and system research based on Digital projection optical grating [D].Wuhan: Huazhong University of Science and Technology, 2009.(in Chinese)

[5] REICH C, RITTER R, THESING J. 3-D shape measurement of complex objects by combining photogrammetry and fringe projection[J]. Optical Engineering, 2000,39(01): 224-231.

[6] 梁晋, 肖振中, 臧顺来, 等. 外差式多频相移技术的三维光学点云测量研究[J]. 锻压技术, 2008, 33(1): 143-147.

LIANG Jin, XIAO Zhen-zhong,ZANG Shun-lai, et al. Study on 3D optical points dense cloud measuring system based on heterodyne multiple frequency phase shift technology [J]. Forging Technology, 2008, 33 (1): 143-147. (in Chinese with an English abstract)

[7] 邾继贵, 郭磊, 叶声华. 现场条件下大空间三维精密定位原理与方法[J]. 光学学报, 2009, 29(7): 1872-1876.

ZHU Ji-gui, GUO Lei, YE Sheng-hua.Principle and implementation method of three-dimensional precision positioning in large field working space[J]. Acta Optica Sinica,2009, 29 (7): 1872-1876. (in Chinese with an English abstract)

[8] SONG L, DONG X, XI J, et al. A new phase unwrapping algorithm based on three wavelength phase shift profilometry method[J]. Optics & Laser Technology, 2013, 45: 319-329.

[9] 张雨薇. 基于结构光的物体三维形貌测量[D].哈尔滨： 哈尔滨工程大学, 2012.

ZHANG Yu-wei. Research on three-dimensional topography measurement using structured light [D]. Harbin: Harbin Engineering University, 2012.(in Chinese)

[10] GHIGLIA D C, PRITT M D. Two-dimensional phase unwrapping: theory, algorithms, and software [M]. New York: Wiley, 1998.