Risley棱镜在光学侦察中的应用

洪华杰,周 远，陶 忠，范大鹏，范世珣

(1. 国防科技大学 机电工程与自动化学院，湖南 长沙410073;2. 西安应用光学研究所，陕西 西安 710065)

1 光电侦察领域中的光学平台技术

光电侦察技术利用光源在目标和背景上的反射或目标、背景本身辐射电磁波的差异来探测、识别目标，成为继雷达技术之后的另一种非常有效的战场侦察手段。近年来，微光、激光、红外等光学成像技术不断更新，各式新型的光电器件日新月异，配以形形色色的光学平台，光电侦察的手段越来越丰富。

光学平台技术一般可分为平台式和指向镜式。平台式[1-5]是图像或瞄准线稳定的一种成熟技术，一般将探测器和惯性器件集成于一个多轴万向架上，通过控制探测器平台的运动实现光束或视轴的空间运动，获取稳定的图像或视轴。这种万向架平台技术在过去几十年内得到了广泛应用，著名的阿帕奇武装直升机上的光电观瞄装置就是采用这种方式。但是平台式需要将探测器与惯性器件暴露于掩体外，战场上易受攻击，同时由于惯量较大，整体稳定的快速性能受影响，平台式的动静态性能似乎已接近极限，这已逐步不能满足高速高精度光电侦察领域的需求。现代光学平台技术的研究关注点正投向各类指向镜式的光学平台技术[6-8]，反射镜稳定技术、快速反射镜技术、新型楔镜光束调整技术等，都是在光学通道中置入某类型的光学器件，通过控制该光学器件的姿态来实现光束或视轴的空间运动。

反射镜稳定技术是把光学传感器安装在万向架中的固定位置，将反射镜安装在光学传感器光路中，光轴的方向可以由受控反射镜的姿态变化来改变。世界各国坦克车辆中的光电侦察装置大都采取这种方式。文献[9-12]较为全面地论述了反射镜稳定的多种技术手段，剖析了从传统的二比一机制、到摒弃传动机构的仿捷联式机制下视轴稳定的系统构成与数学原理，并分析了各种稳定机制的优缺点。二比一机构和捷联方式均为系统引入了更多的误差源，致使反射镜机制下的系统稳定性能难以超越平台式。尽管在近一二十年内其应用研究日趋减少，但是反射镜稳定方式下的系统轻量化、配置灵活的优势使得其始终是军用光电侦察领域中的一种有效手段。

快速反射镜是指转角范围在毫弧度量级，分辨率和重复定位精度在亚微弧度或微弧度量级，位置伺服带宽达到100 Hz以上的光轴控制机构。快速反射镜属于典型的定位系统，主要应用于光电平台二级稳定以及精密光束指向控制系统中，与粗级光学平台或反射镜稳定平台一起构成粗精复合稳定系统[13-17]。根据致动器类型，用于精密光路调整和稳定的快速反射镜机构可分为6大类：压电陶瓷致动器(piezoelectric transition , PZT)、音圈电机(voice coil actuator， VCA)、磁致伸缩致动器、形状记忆合金致动器、电致伸缩致动器、静电微致动器。国内外研究现状表明，目前用于角度快速调整的精瞄偏转微定位机构，以压电陶瓷致动和音圈电机致动为主。国外开展快速反射镜的研究和产品开发较早，目前技术水平领先的有德国PI公司、美国洛克希德-马丁空间系统公司、英国Queensgate设备公司、德国的MRC Systems股份有限公司、BAE SYSTEM公司、美国Ball Aerospace & Technology公司和日本NEC公司等[14]。国内开展此类研究相对较晚，但进展较大，目前中科院长春光学精密机械与物理研究所、哈尔滨工业大学和国防科技大学等多家单位正在进行精密光路调整机构的相关研究。

棱镜利用了光学折射原理，人们通过各种光学组合来控制光束的指向。近些年来，以棱镜为基础的光学技术已逐步应用于军事领域，成为光学战场侦察的一种有效手段。本文就Risley棱镜为对象，描述了其组成、工作原理、工程实现问题及其应用等现状，为其进一步应用研究奠定基础，也可供同行参考。

2 Risley棱镜的工作原理

Risley棱镜系统通过两棱镜的共轴独立旋转改变光的传播方向，可实现光束或视轴的指向调整[5]。

2.1 系统构成

如图1所示，Risley棱镜光束指向控制系统的核心由一对共轴相邻排列的折射棱镜组成，该棱镜组在轴承的支撑下由各自的电机驱动绕共同的轴旋转，一般配有测量棱镜实时位置的测角元件，有时还配置测速元件等。

文献调研表明，一般系统设计中两棱镜的顶角和材料相同，可采用面对面或背靠背式的配置方式，两棱镜尽可能贴近以减小光轴平移误差[18]。同时两棱镜一般配置在机架的轴端，以减小外侧光线的遮挡。

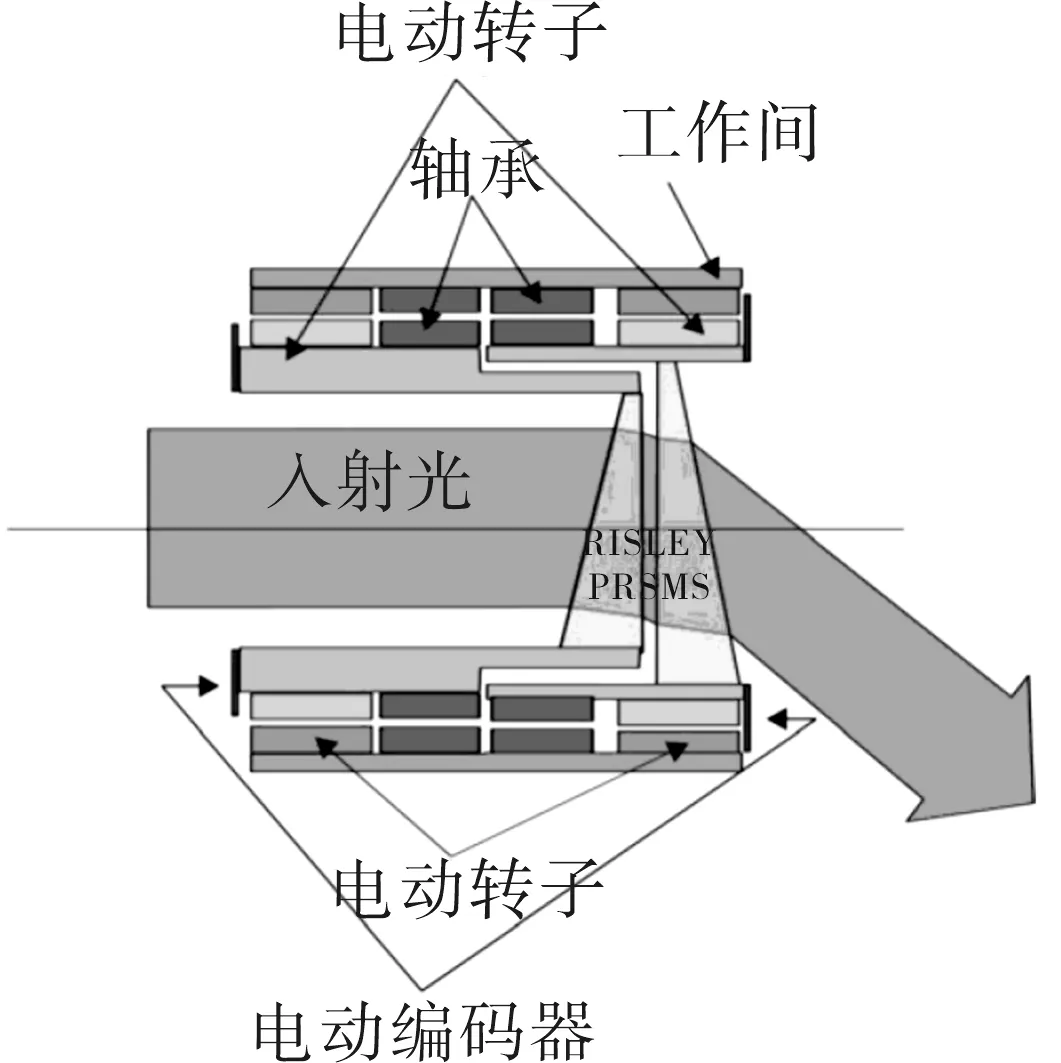
图1 Risley棱镜光束控制系统构成示意图Fig.1 Structure of beam control system for Rislay prism

2.2 Risley棱镜光束控制工作原理

系统工作原理如图2所示。光束平行系统转轴入射，两棱镜将通过折射改变光束传播方向。通过改变两棱镜的转角θ1、θ2，可使出射光束在一定偏转角范围内实现任意指向调整。寻求两棱镜的方位与出射光束指向位置之间的内在联系是Risley棱镜光束调整系统应用的中心问题[19]。当平行光线射入棱镜系统，已知两棱镜的位置求取出射光线的偏转角度是Risley棱镜光束调整系统的正求解问题。当已知所要求的出射光束偏转角度求取两棱镜的角度是Risley棱镜的反求解问题[20-21]。

1) 正求解问题

解决正求解问题的传统方法是一级近轴近似方法，将两棱镜都看作楔角很小的光楔，光束在棱镜主截面内偏转恒定的角度，双棱镜系统对光束总的偏转角度就是两棱镜偏转角度的矢量和[22-24]。该方法是近轴条件下的薄棱镜近似，只适用于偏转角较小的双棱镜系统。近期Yang 和 Li 采用光线追迹方法分别对不同结构的双棱镜系统推导了光束指向随双棱镜角度位置变化的解析关系式，为双棱镜系统的大角度偏转应用提供了理论基础和方法导引[19,21]。

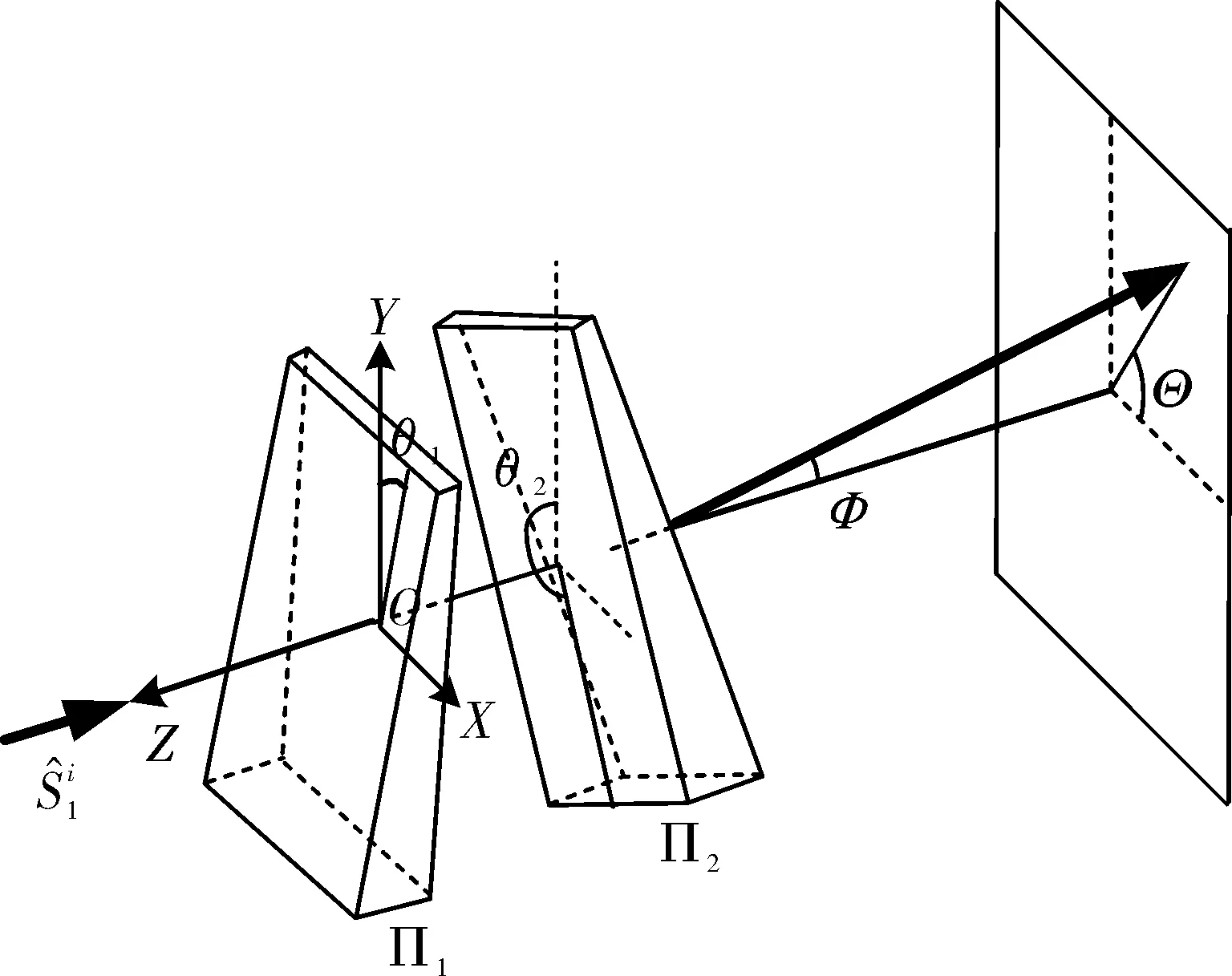
图2 Risley棱镜光束控制示意图Fig.2 Beam controlling diagram of Rislay prism

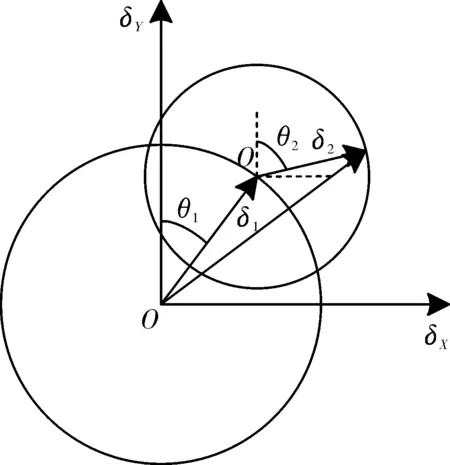
图3 光束偏转的远场薄棱镜近似分析方法Fig.3 Approximate analysis of beam deflection far-field thin prism

依据远场薄棱镜近似分析方法，由图3可知，经过2个棱镜后的光束在2个方向上的偏转角度分量分别为

Φx=δ1sin(θ1+θ10)-δ2sin(θ2+θ20)
Φy=-δ1cos(θ1+θ10)+δ2cos(θ2+θ20)

(1)

式中：每个棱镜的光束偏转角大小分别为δ1=α1(n1-1)；δ2=α2(n2-1)；θ1、θ2分别为前后2个棱镜y轴绕z轴的转角，θ10、θ20分别为两转角的初始值。

当棱镜转角的初始值、实时值以及δ1、δ2已知后，可以确定光束的偏转角度。

2) 反求解问题

在给定光束目标指向位置的偏转角Φ和方位角Θ时，可利用中心算法求反向的方法，推导两棱镜的旋转角度θ1和θ2，其计算原理如图4所示。

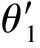
图4 中心算法求反解问题的近似解析解Fig.4 Approximate analytical solution of inverse solution with center algorithm

由几何关系容易求得三角形两内角α和β为

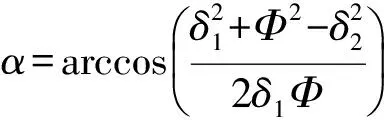
(2)

两套解分别为

(3)

2.3 Risley棱镜应用技术

2.3.1 利用反求解的视轴步进成像控制技术

在传统的光电成像侦察技术中，存在大视场和高分辨率的不可调和的矛盾，一直是影响光电侦察效率的一个重要因素之一。目前一般是采用双视场的探测器来解决这个矛盾，一个低分辨率宽视场用于战场的大范围观察，一个高分辨率窄视场用于目标的识别与跟踪。2个视场可以形成互补，但是2个视场之间的切换时间较长，应用受限。

利用Risley棱镜反求解的视轴步进成像技术，窄视场通过视轴的高速步进扫描拼接成大视场图像，图像中保留了窄视场的高分辨率的特点。文献[25]给出了图5所示的步进扫描成像的简单思路：① 确定棱镜的初始姿态，完成图像A采集；② 建立镶嵌图，擦除之前的图；③ 估计下一位置，改变棱镜姿态角；④ 以此类推，通过多次循环，通过图像镶嵌拼接获取图像B。

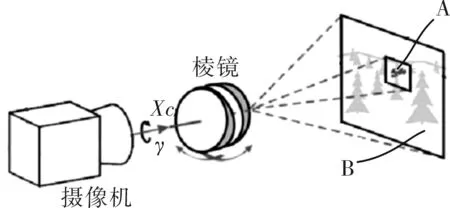
图5 视轴步进成像技术示意图Fig.5 Diagram of optical axes step imaging technology

但是文献[26]中指出，单次捕获的图像A不能直接镶嵌至大图像中，因为在成像过程中，目标区域A所成图像会有畸变，这个畸变是影响成像质量的重要因素之一。为此，文献[26]按照图6从理论上研究了单楔镜成像时的畸变规律，得出了实际成像时的位置偏差结果符合公式(4)的规律：

图6 图像畸变效果的计算示意图Fig.6 Calculation schematic diagram of image distortion effect

(4)

式中：I为入射光轴与光楔第一面的法线间夹角；光楔的出射光轴相对于入射光轴偏转δ角；光楔的顶角为α；折射率为L。

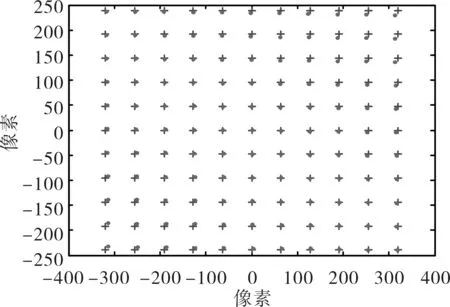
图7 图像畸变结果图Fig.7 Result of image distortion

由(4)式可以看出，实物平面上不同坐标处所成像素的偏差大小与其坐标值大小有关，这很好解释了部分文献中所描述的“实物平面中的正方向成像后看到的是侧边凹(凸)的钟形”[26]。利用公式(4)生成的图7展示了验证图像畸变效果，图中十字线为理想成像点，原点为实际成像点。因此消除图像畸变是步进成像的关键任务之一。

2.3.2 利用正求解的光束扫描控制技术

利用Risley棱镜的正求解特性，可以实现区域的光束快速覆盖。一般设计中2个棱镜结构参数完全一致，当初始角均为π/2，则公式(1)演变为

Φx=δcosθ1-δcosθ2
Φy=δsinθ1-δsinθ2

(5)

当2个棱镜的转角相等时，公式(5)可以看出2个偏转角始终为0，能够保证通过棱镜的光束不改变方向。

当改变2个转镜的转速方向和大小比例时，光束则按照一定的规则覆盖一定的区域。设转镜1转速为ω，转镜2转速为kω(k可为正负)，则有：

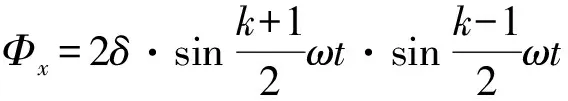
(6)

当转速系数k为负数时轨迹计算结果如图8所示，光束扫描线为梅花瓣状，花瓣的大小随着系数绝对值的增加而变大。当转速系数k为正时的轨迹计算结果如图9所示，此时光束扫描线呈现类螺旋线。

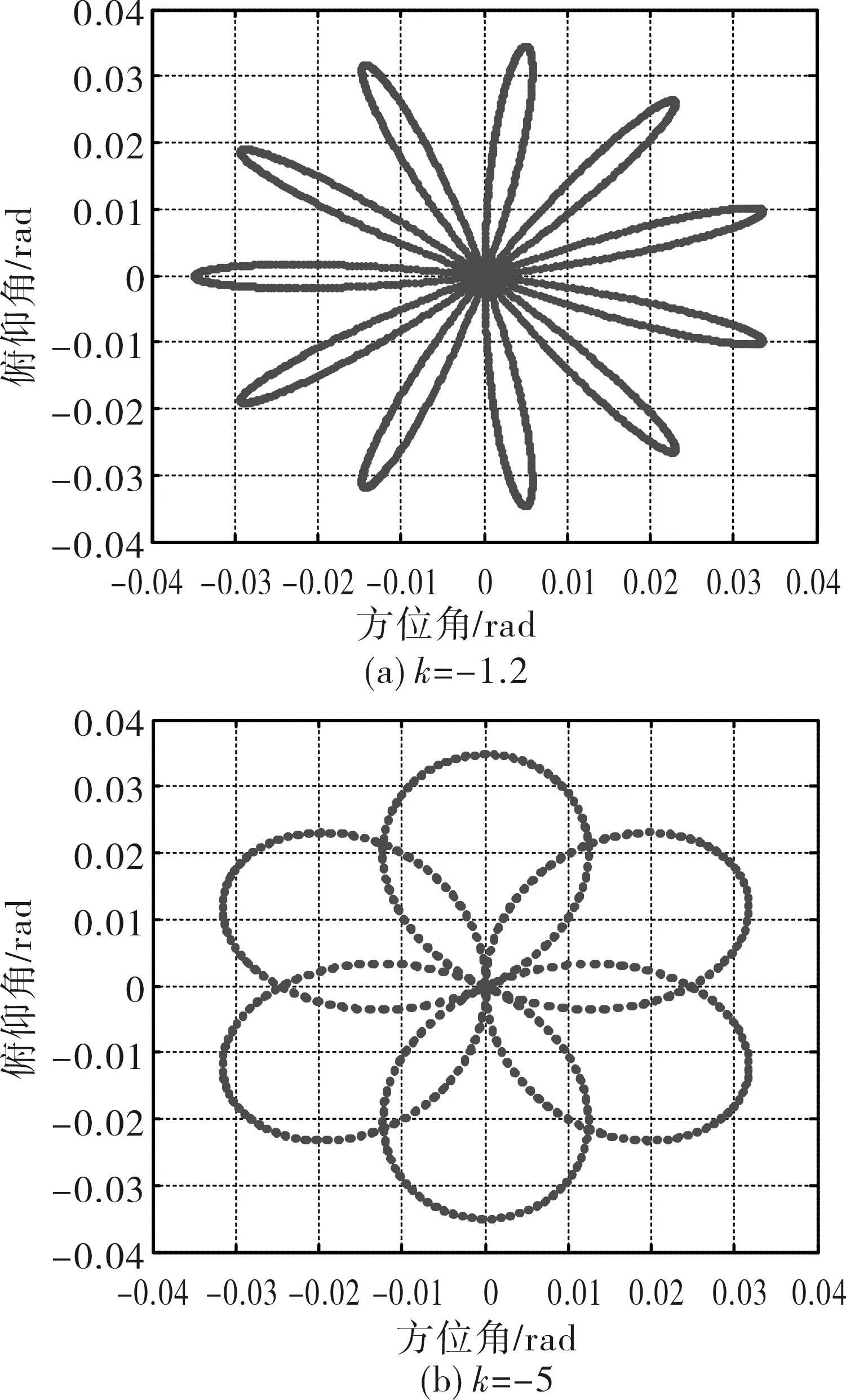
图8 速度系数为负时的光束扫描轨迹Fig.8 Beam scanning trace with negative velocity coefficient

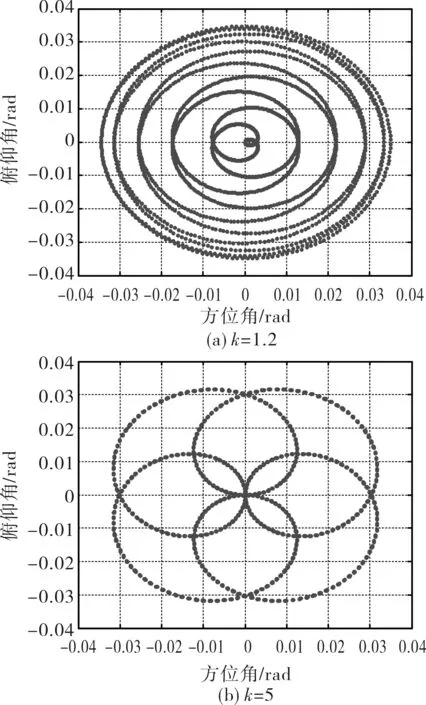
图9 速度系数为正时的光束扫描轨迹Fig.9 Beam scanning trace with positive velocity coefficient

由于棱镜组运动速度较快，能够使得一个光束在很短时间内按照既定的轨迹覆盖一定的区域，形成光束扩散效应，因此可在激光雷达、医疗探测等方面得到应用。

3 Risley棱镜系统面临的主要工程技术问题

从原理上Risley棱镜可以实现光束步进成像和光束扫描等技术应用，但是从工程角度而言，基于棱镜的大角度光束偏转指向仍存在一些机械、控制及光学方面的工程技术问题，还有待深入探讨[27]。

3.1 棱镜加工与装配误差

理论上当两棱镜的顶角、折射系数完全相同且理想装配时，棱镜系统才可实现光束指向的全区域覆盖。但是由于加工误差、装配误差及热学性能等因素的影响，两棱镜光束偏转角难以完全抵消，会产生指向盲区。盲区大小取决于棱镜的加工精度和装配精度，中心轴附近的盲区大小可达几到几百微弧度。高精度光束指向系统要求具有较高的加工和安装精度并在系统设计时需考虑和减弱环境的影响。

3.2 光机电综合设计优化与协同控制

旋转双棱镜光束指向系统涉及光学、机械、控制、传感、图像信息处理等多学科，为达到最优性能，需要多学科的优化设计和协同控制。在光束指向应用中，需要结合光束传输、机械动态特性、伺服机构性能、控制性能来实现系统的综合设计。在成像应用中，除考虑上述因素外，还需考虑成像性能需求、图像信息的传输与处理等。

在远离中心轴的光束指向区域，存在非线性的伺服控制问题。与传统的万向架或指向镜系统不同，双棱镜系统对光束的最终转向角度与棱镜旋转角度之间的关系是非线性的，导致棱镜旋转控制方程的非线性。目前实现非线性控制的基本思路是利用查表法或局部线性算法逆解控制方程求解，获得棱镜旋转方位。光束偏转角与棱镜旋转角的非线性关系加大了系统控制难度，需要设计复杂的控制算法以满足应用中光束转向需求。

3.3 棱镜的光学成像特性

旋转双棱镜系统必须解决的一个重要光学设计问题是色差校正。光束转向应用中，由于操作对象大多为激光光束，其单色性较好，色差影响较小。但在步进成像应用中，成像光的波段宽，棱镜导致的色差将明显降低成像像质，必须以特殊结构的棱镜实现色差校正。而该系统的色差校正面临4个方面的问题：大角度光束偏转、宽波段覆盖、系统质量和结构紧凑性、材料选择及加工可行性。光束偏转角越大，消色差波段越宽，色差校正的难度越大。传统组合棱镜方法虽能有效实现色差校正，但也增加了系统体积和质量，系统的紧凑性和轻便性受到影响，限制了其实际应用，这在可见和近红外波段表现尤其明显。衍射光学元件方法仅在棱镜表面蚀刻光栅结构，能有效减小系统体积和质量，但同时也增大了加工难度。

在成像应用中，大角度视轴偏转下的成像畸变现象严重。为获取完整大视场、高分辨率的图像，必须采用适合方法对成像畸变予以校正。

热稳定性能也是旋转双棱镜光束指向系统需要关注的问题。在温度变化的环境下，系统对光束的偏转角随环境温度改变，光束指向的稳定性受到影响。

4 Risley棱镜样机的研制

4.1 国外典型产品与应用

自Rosell于1960年首次提出利用两块棱镜实现光束扫描以来，旋转双棱镜逐渐被作为指向装置应用在不同领域，面向不同应用需求的产品逐渐问世。美国已有多家研究机构针对旋转双棱镜大角度光束指向展开了研究，开发了面向红外对抗、机载激光通信、扫描与跟踪等应用的装置。这些装置主要的应用领域也是集中于步进成像和光束扫描2个方面。

图10 国外Risley棱镜方面的产品Fig.10 Foreign Rislay prism products

加拿大国防技术研究与发展中心利用旋转双棱镜构建了步进-凝视成像系统，形成了一种新型的多视场图像采集方法。图11展示了旋转双棱镜指向机构外观图。系统利用旋转双棱镜改变成像光轴，在较大角度范围内实现视轴扫描。通过合理设置成像视轴的空间指向角度和窄视场分块成像，获得系列高分辨率窄视场图像，通过窄视场图像的校正和拼接，最终获得具有大视场和高分辨率特点的合成图像。该系统利用旋转双棱镜构造光机指向机构，用于成像视轴的转向和扫描。通过融合窄视场成像，兼顾了大视场和高分辨率的成像需求，为大范围目标搜索和高准确度目标识别应用提供了一种新概念图像采集方法。

图11 步进凝视图像采集方法及旋转双棱镜指向机构Fig.11 Step staring imaging collection method and rotating biprism pointing structure

1981年美国国家航空航天局NASA将一对锗光楔作为激光光束扫描器用于激光雷达系统中，原理如图12所示。飞行测试表明该雷达能在20°范围内实现光束扫描，其指向误差小于0.1°。同年美国林肯实验室将旋转双棱镜用于三维成像激光雷达系统，作为激光光束扫描器以扩大观测场。该扫描器使雷达能在10.8°的观测覆盖范围内实现高分辨率三维成像。美国Sigma空间公司研制的三维成像激光雷达将旋转双棱镜用作光束扫描器，其重复扫描精度达到0.000 5°。近来还有专利报道了旋转双棱镜在机载光收发机构中的具体应用。

图12 激光雷达中的旋转双棱镜扫描器Fig.12 Rotating biprism scanner in Ladar

4.2 国内相关应用开发情况

4.2.1 整体情况

国内的相关研究起步也不晚，对旋转折射棱镜组的研究集中在旋转光楔对的折光特性、控制模型及其应用分析上。中国科学院上海光学精密机械研究所的刘立人研究员为首的研究组针对星间激光通信应用需求设计了光束扫描机构(如图13)，研究了棱镜回转控制模型并测试了其目标捕获、跟踪、指向及激光通信性能。同济大学的李安虎博士探讨了双光楔光束偏转及控制方法并改进了旋转双棱镜扫描机构，实现了激光光束的粗精复合扫描。南京航空航天大学的林有义教授研究了旋转双光楔在全息成像中的应用。华南师范大学的韦中超探讨了旋转双光楔的二维扫描轨迹。上海激光技术研究所的潘涌研究了旋转双光楔在激光微孔加工中的应用。北京理工大学的李岩等探讨了利用Risley棱镜补偿成像误差的基本理论。以上国内学者的研究大都是以扫描成像为目的，针对光束小偏转角的应用，而利用旋转棱镜组实现大偏转角调整方面的研究偏少。

图13 用于星间激光通信的旋转双棱镜光束扫描机构Fig.13 Rotating biprism beam scanning device used for inter-satellite laser communication

4.2.2 国防科技大学的研究情况

国防科技大学机电工程与自动化学院一直跟踪双旋转棱镜系统的技术发展，在2010年研制出一台双旋转棱镜样机，如图14所示。

图14 国防科技大学研制的双旋转棱镜样机Fig.14 Risley prism prototype developed by national university of defense technology

该样机口径为70 mm，光束偏转角为10°，具备两种工作模式：步进成像和光束扫描。样机完成了两项功能实验，步进成像结果如图15所示，光束扫描实验结果如图16所示。

图15 视轴步进成像实验结果图Fig.15 Experiment result of optic axes step imaging

图15中的大图是步进镶嵌图像，其上方的小图是大图中的一格。通过步进成像不失分辨率地获得了所关心的大区域图像。图16中激光器从样机后方射入，光点照射在地图上。当样机高速扫描时，光点运动形成的轨迹被相机所捕获，瞬时图像如图16(b)所示。

图16 光束扫描实验结果图Fig.16 Experiment result of beam scanning

当然作为一个样机，系统仍然存在不完善的地方。如图像采集频率受限、棱镜表面精度不高等，都会影响成像质量和扫描效果。

5 结束语

基于Risley棱镜的光学系统已不是一个新生事物，国内外应用较为广泛，近年来Risley棱镜在军事上的应用尤其引人关注。论文阐述了Risley棱镜的两种工作原理，并给出了仿真计算结果，从宏观上归纳了其工程实现的难点，介绍了国内外的工程应用情况，特别是介绍了国防科技大学的工程样机研制情况，给出了2种实验的结果。

[1] 孙辉，郎小龙，李志强. 动载体光电平台视轴稳定精度的检测[J]. 光学精密工程， 2011, 19(9): 2131-2137.

SUN Hui,LANG Xiao-long,LI Zhi-qiang. Measurement for LOS stabilization accuracy of electro-optical imaging system on moving carrier[J]. Optics and Precision Engineering, 2011, 19(9): 2131-2137.(in Chinese with an English abstract)

[2] 李焱，曹立华，王弟男. 惯导平台下舰载光电搜索跟踪系统的控制[J]. 光学精密工程， 2011, 19(5): 1126-1133.

LI Yan,CAO Li-hua,WANG Di-nan. Controlling of shipborne optoelectronic searching and tracking system based on inertial navigation platform[J]. Optics and Precision Engineering, 2011, 19(5): 1126-1133. (in Chinese with an English abstract)

[3] CHEN C B. Beam steering and pointing with counter-rotating grisms [J]. SPIE, 2007, 6714: 671409.

[4] WINSOR R, BRAUNSTEIN M. Conformal beam steering apparatus for simultaneous manipulation of optical and radio frequency signals[J]. SPIE, 2006, 6215: 62150G.

[5] SCHWARZE C R, VAILLANCOURT R, CARLSON D, et al. Risley-prism based compact laser beam steering for IRCM, laser communications, and laser radar[EB/OL]. 2005-09-10[2011-03-20]. http://www.optra.com/images/TP-Compact_Beam_Steering.pdf.

[6] ULANDER K. Two-axis beam steering mirror control system for precision pointing and tracking applications[D]. California :Faculty of California Polytechnic State University , 2006.

[7] KIM B S, GIBSON S, TSAO T. Adaptive control of a tilt mirror for laser beam steering [C]. Boston: AACC,2004.

[8] LLOYD W B, BALTIMORE M D. Inertially stabilized heliostat assembly:USA, 3951510[P]. 1976-4-20.

[9] 洪华杰 王学武，翁干飞. 军用光电侦察的反射镜稳定技术[J]. 应用光学，2011，32(4)：591-597.

HONG Hua-Jie, WANG Xue-Wu, WENG Gan-Fei .Mirror stabilization in electro-optical reconnaissance system[J] Journal of Applied Optics, 2011, 32(4): 591-598. (in Chinese with an English abstract)

[10] HILKERT J M. A comparison of inertial line-of-sight stabilization techniques using mirror[J]. SPIE, 2004,5430: 13-22.

[11] ROYALTY J. Development of kinematics for gimbaled mirror systems[J]. SPIE,1990, 1304: 262-274.

[12] DEBRUIN J C. Derivation of line-of sight stabilization equations for gimbaled-mirror optical systems[J]. SPIE ,1990,1304: 262-274.

[13] 张丽敏，郭劲. 快速反射镜双X-Y轴控制的仿真研究[J]. 光学精密工程, 2005, 13(增刊):142-147.

ZHANG Li-min,GUO Jin.Simulative research on dual X-Y axis control of fast steering mirror[J]. Optics and Precision Engineering, 2005, 13(z1): 142-147. (in Chinese with an English abstract)

[14] 朱华征，范大鹏，张智永． 精密光路偏转及焦距调整机构的发展[J]． 激光与红外, 2009, 39(10)：1028-1033.

ZHU Hua-zheng,FAN Da-peng,ZHANG Yong-zhi,et al. Development of precise light beam steering and focusing equipments[J].Laser & Infrared, 2009, 39(10)：1028-1033. (in Chinese with an English abstract)

[15] 马佳光. 捕获跟踪与瞄准系统的基本技术问题[J]. 光电工程, 1989,16(3):1-41.

MA Jia-guang.The basic technologies of the acquisition tracking and pointing systems[J]. Opto-Electronic Engineering, 1989, 16(3):1-41. (in Chinese with an English abstract)

[16] 张丽敏，郭劲，陈娟. 快速控制反射镜结构研究综述[J]. 光机电信息,2005(8): 21-24.

ZHANG Li-min GUO Jin, CHEN Juan. Summary of the mechanic structure for fast-steering mirrors [J].OME Information, 2005(8): 21-24. (in Chinese with an English abstract)

[17] 傅承毓，姜凌涛，任戈,等. 快速反射镜成像跟踪系统[J]. 光电工程， 1994，21(3)：1-8.

FU Cheng-yu, JIANG Ling-tao ,REN Ge, et al. Image tracking system with a fine-steering-mirror[J]. Opto-Electronic Engineering, 1994，21(3)：1-8.(in Chinese with an English abstract)

[18] PRINCE J B, DETRO S M. Beam manipulation using sets of wedges:USA, 7319566B2[P]. 2006-01-15.

[19] YANG Y. Analytic solution of free space optical beam steering using Risley prisms[J]. Journal of Lightwave Technology,2008, 26(21): 3576-3583.

[20] LI Y. Third-order theory of the Risley-prism-based beam steering system[J]. Applied Optics, 2011, 50(5): 679-686.

[21] LI Y. Closed form analytical inverse solutions for Risley-prism-based beam steering systems in different configurations[J]. Applied Optics,2011, 50(22): 4302-4309.

[22] SCHWARZE C. A new look at Risley prisms[J]. Photonics Spectra, 2005, 40(6): 67-70.

[23] JENKINS F R, WHITE H E. Fundamentals of optics[M].4th ed. New York: McGraw-Hill Companies, Inc., 2001.

[24] BOISSET G C, ROBERTSON B, HINTON H S. Design and construction of an active alignment demonstrator for a free-space optical interconnect[J]. Photonics Technology Letters, 1995, 7(6): 676-679.

[25] LAVIGNE V, RICARD B. Step-stare image gathering for high-resolution targeting[R]. France:NATO, 2005.

[26] 毛文炜. 位于平行光路中的光楔产生的畸变[J]. 清华大学学报:自然科学版,1999，39(4): 42-45.

MAO Wen-wei. Distortion of wedge prisms in collimated beam[J]. Journal of Tsinghua University:Science and Technology, 1999，39(4): 42-45. (in Chinese with an English abstract)

[27] OSTASZEWSKI M, HARFORD S, DOUGHTY N, et al. Risley prism beam pointer[J]. SPIE, 2006, 6304: 630406.