分数阶时滞广义Logistic方程解的研究*

袁利国

(华南农业大学数学系, 广东 广州 510642)

最近20年，分数阶微分系统的理论与应用引起学者的广泛研究[1-17]。由于分数阶微积分的非局域性，与整数阶微积分相比，分数阶微积分能更好地刻画一些现实问题，其中部分文献用分数阶微积分的理论来研究生物种群的变化规律[1-7]。同时, 在生物系统中时滞现象也大量存在，因此研究分数阶时滞系统有实际意义[3,5-6]。DAS S等[1]利用同伦扰动方法给出了分数阶广义Logistic方程的近似解析解。程媛媛与蒋威[3]研究了一类分数阶时滞单种群模型的平衡点的局部稳定性。EL-SAYEDABBAS等[2,4]研究了分数阶Logistic方程及其改进模型的动力学。EL-SAYED 与SWEILAM等[5-6]研究了分数阶双时滞Logistic方程解的存在性、稳定性与数值解。本文研究如下分数阶时滞广义Logistic方程[1,5]

(1)

1 预备知识

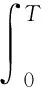
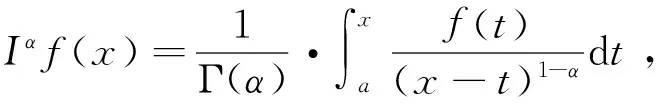
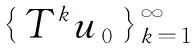
2 解的存在唯一性与稳定性

基于EL-SAYED A M A等[5]的文献中方法，假设对初值问题(1)定义C(I)={x∈R:x(t)∈[0,1],t∈I},且t≤0时，有x(t)=x0成立，则有如下结论。

证明基于分数阶微积分性质,分数阶时滞微分方程(1)可写成

对此方程的两边同时作用积分算子Iα,得

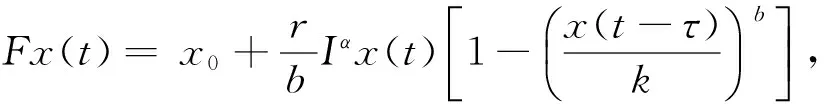
e-Nt|Fx(t)-Fy(t)|=

(2)

记

则

(3)

[y(s)yb(s-τ)-x(s)xb(s-τ)]ds|=

做变换s-τ=θ，得

[y(θ+τ)yb(θ)-y(θ+τ)xb(θ)+

y(θ+τ)xb(θ)-x(θ+τ)xb(θ)]dθ|≤

(4)

记

而yb(θ)-xb(θ)=bξb-1(θ)|y(θ)-x(θ)|，其中ξ(θ)落在y(θ)与x(θ)之间，由于|x(θ)|<1 与|y(θ)|<1，得

|y(θ)-x(θ)|dθ≤

令t-θ-τ=h，则

(5)

而

|y(θ+τ)-x(θ+τ)|dθ≤

(6)

基于以上分析(2)-(6)及范数定义，得

‖Fx(t)-Fy(t)‖≤A1+A2≤A1+B1+B2≤

(7)

即

定理2 方程(1)的解是一致稳定的。

证明假设y(t)是如下分数阶时滞广义Logistic微分方程的解

(8)

则

x(t)-y(t)=(x0-y0)+

两边同时乘上e-Nt，并取绝对值,利用范数定义与定理1的结论,得

‖x-y‖≤|x0-y0|+

因此

即当初始值|x0-y0|<ε，则解‖x-y‖≤δ(ε)成立，故方程(1)的解是一致稳定的。

3 数值解

基于改进的Adams-Bashforth-Moulton预估-校正算法[15-16], 下面给出

(9)

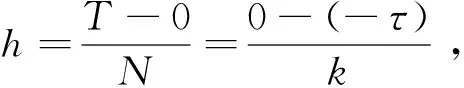
yh(tj)=y0，(j=-k,-k+1,…,-1,0)；

yh(tj-τ)=yh(jh-kh)=yh(tj-k)，

(j=0,1,…,N)

假设已经计算得到近似值yh(tj)≈y(tj) (j=-k,-k+1,…,-1,0,1,…,n)，对原方程(9)的两边同时作用积分算子，并利用yh(tn)≈y(tn)，则

(10)

对(10)式中的积分项利用product trapezoidal quadrature公式，得校正表达式

(11)

其中

aj,n+1=

(12)

(13)

其中

(14)

结合 (11)-(14) 式，得到(9) 式的数值解yh(tj)(j=-k,-k+1,…,-1,0,1,…,N)。

现对x(t)仅限制大于0，固定参数值α=0.9,b=1,r=0.5,k=1,τ=7,T=80，利用Matlab编程得数值解，如图1所示。

图1 数值解Fig.1 Numerical solution

4 结 论

非线性分数阶时滞微分方程的解的研究还较少，且其精确解通常很难求得。本文得到了非线性分数阶时滞广义Logistic方程解的存在唯一性及其解的一致稳定性的充分条件，同时利用改进的Adams-Bashforth-Moulton 预估-校正算法给出其数值解，结合Matlab编程实现数值模拟。对非线性分数阶时滞方程解的更一般理论还须进一步研究。

[1] DAS S, GUPTA P K, VISHAL K. Approximate approach to the Das model of fractional logistic population growth [J]. Appl Appl Math, 2010, 5(10)：1702-1708.

[2] EL-SAYED A M A, EL-MESIRY A E M, EL-SAKA H A A. On the fractional-order logistic equation [J]. Appl Math Lett, 2007, 20: 817-823.

[3] 程媛媛，蒋威. 分数阶时滞单种群模型的稳定性[J]. 佳木斯大学学报, 2012, 30: 468-473.

[4] ABBAS S, BANERJEE M, MOMANI S. Dynamical analysis of fractional-order modified logistic model [J]. Comput Math Appl, 2011, 62: 1098-1104.

[5] EL-SAYED A M A, EL-SAKA H A A, EL-MAGHRABI E M. On the fractional-order logistic equation with two different delays [J]. Z Naturforsch, 2011, 66a: 1-5.

[6] SWEILAM N H, KHADER M M, MAHDY A M S. Numerical studies for fractional-order logistic differential equation with two different delays [J]. J Appl Math, 2012, ID 764894: 1-14.

[7] SWEILAM N H, KHADER M M, MAHDY A M S. Numerical studies for solving fractional-order logistic equation [J]. Int J Pure Appl Math, 2012, 78: 1199-1210.

[8] ZHANG X Y. Some results of linear fractional order time-delay system [J]. Appl Math Comput, 2008, 197: 407-411.

[9] 刘丽琼，钟守铭，索宇. 线性分数阶多时滞系统的解的存在唯一性[J]. 西南民族大学学报, 2011, 37: 719-721.

[10] 黄郑，蒋威. 一类分数阶时滞微分系统的解[J]. 合肥学院学报, 2012, 22: 8-10.

[11] 杨水平. 关于分数阶多阶延迟微分方程的解的存在性[J]. 惠州学院学报, 2011, 31: 29-31.

[12] 魏谞婷，卢旋珠. 一类广义分数阶时间迟滞微分方程的一些结果[J]. 福州大学学报, 2010, 38: 166-171.

[13] DENG W H, LI C P, LU J H. Stability analysis of linear fractional differential system with multiple time delays [J]. Nonlinear Dynam, 2007, 48: 409-416.

[14] KILBAS A A, SRIVASTAVA H M, TRUJILLO J J. Theory and applications of fractional differential equation [M]. New York: Elsevier, 2006.

[15] BHALEKAR S, DAFTARDAR-GEJJI V. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order [J]. J Fract Calc Appl, 2011, 6: 1-9.

[16] DIETHELM K, FORD N J, FREED A D. A predictor-corrector approach for the numerical solution of fractional differential equations [J]. Nonlinear Dynam, 2002, 29: 3-22.

[17] 王金华，赵育林，向红军. 分数微分方程m点边值问题解的存在性与唯一性[J]. 中山大学学报：自然科学版, 2011, 50(1): 4-8.