LQG/LTR控制在二级倒立摆系统中的应用研究

崔 挺,严运兵,肖小城

(1.武汉科技大学汽车与交通工程学院，湖北 武汉，430081；2.奇瑞新能源汽车技术有限公司，安徽 芜湖，241002)

倒立摆系统是一个典型的非线性、强耦合、多变量、不稳定的系统，是进行控制理论研究的典型实验平台。倒立摆系统控制是控制理论发展中的一个典型问题，其控制实验可以验证许多新的控制理论[1]。目前，通过倒立摆系统验证过的许多控制方法在航天、机器人以及一般工业过程领域均有着广泛的应用，如航天飞机的姿态控制、机器人行走过程中的平衡控制等，故倒立摆系统控制实验已成为控制理论界学者研究的热点。

对于控制系统而言，控制律的形成需要系统的状态变量，而状态变量需要通过量测装置进行观测，但量测装置中存在着随机干扰。LQG/LTR控制是一种现代多变量频域的设计方法，它能有效处理有附加噪声影响或状态变量不能直接量测的线性系统控制问题，其良好的鲁棒性和解耦特性使得该控制方法在鲁棒控制系统设计中得到广泛应用，有着很高的工程实用价值[2]。为此，本文以二级倒立摆系统为例，采用LQR状态反馈与卡尔曼状态估计相结合的方法，通过回路传输恢复技术(LTR)弥补LQG设计的不足，完成了LQG/LTR全状态反馈控制器的设计，并运用MATLAB语言进行仿真分析，将其仿真结果与LQR控制器进行对比，以期验证该设计方法的有效性。

1 LQG/LTR控制理论

1.1 LQG设计原理

线性二次型高斯(LQG)问题是指系统模型用状态空间形式给出的线性系统，其性能指标为基于被控对象和控制输入的二次型函数，所研究的干扰噪声、量测噪声均为独立的高斯密度函数，且噪声以相加的方式加入状态空间模型之中。综合线性二次型控制器(LQR)和卡尔曼滤波器的设计过程，就可设计出LQG动态控制器。

假设对象模型的状态方程为

(1)

若这些信号均为零均值的高斯过程，则其统计特性为

E[w(t)wT(t)]=Ξ≥0

(2)

E[v(t)vT(t)]=Θ≥0

(3)

E[w(t)vT(t)]=0

(4)

LQG问题是寻找一个最优反馈控制律，使得最优控制指标函数式(5)取最小值。即：

(5)

式中：z(t)=Mx(t)为状态变量x(t)的某种线性组合；Q为对称半正定矩阵；R为对称正定矩阵，即Q=QT≥0，R=RT>0。

LQG问题的求解，可分为最优状态估计器Kf和最优状态反馈控制律Kc，其控制系统结构如图1所示。

图1 LQG控制系统结构图Fig.1 Structure of LQG control system

被控对象传递函数G(s)与控制系统传递函数Gc(s)分别为

G(s)=C(sI-A)-1B

Gc(s)=Kc(sI-A+BKc+KfC)-1Kf

(6)

根据分离原理，可将LQG控制器设计分为两步：①选取Kf、Kc中的一个参数设计目标回路，使其满足系统的设计要求；②调整另一个参数使整个闭环回路的性能恢复到目标回路的性能。

Kf=PfCTΘ-1

(7)

式中：Pf为滤波器Riccati方程，并满足：

PfAT+APf-PfCTΘ-1CPf+ΓΞΓ=0

(8)

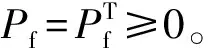
ATPc+PcA-PcBR-1BTPc+Q=0

(9)

MATLAB语言中的鲁棒控制工具箱Kalman和LQR函数可用于解决Riccati方程[3]。

1.2 LTR设计原理

如果加权矩阵Q、R值选择不当，采用卡尔曼滤波器方法与直接反馈获得开环系统的传递函数会出现不同，解决问题的有效方法是在控制策略中引入LTR技术,这样在LQG结构下的开环传递函数就会尽可能接近直接采用状态反馈的传递函数。

在设计模型输入端加入与任意正数q呈正比的虚拟过程噪声，即

W=W0+qΣ,V=I

(10)

式中：W0为实际过程噪声方差的估计值；Σ=ΣT≥0；q为恢复增益。

选择合适的卡尔曼滤波器Kf,调节恢复增益q，使系统开环回路Gc(s)G(s)当q→∞时，在所考虑的频率范围内逼近目标回路Kc(sI-A)-1B曲线，即:

(sI-A)-1B=Kc(sI-A)-1B

(11)

这表明当恢复增益q→∞时，LQG控制器Gc所拥有的鲁棒特性在被控对象的输入端得到了恢复。但在实际应用中，q值不应该选择过大，否则会引起截断误差，破坏系统的鲁棒性。一般情况下，q=1010即可。

根据LQG/LTR理论，回路传输恢复后，系统能够获得对外界干扰和量测噪声更好的鲁棒性，具有增益欲度无穷大和不少于60°相位欲度。

2 仿真与分析

二级倒立摆系统是目前应用相当广泛的控制系统平台,一个典型的二级倒立摆系统主要由机电装置和控制装置两部分组成[4]。机电装置由小车、下摆杆、上摆杆及连接轴等构成。图2为二级倒立摆模型，其工作原理是，用一种控制输入作用在小车上，使小车以一定的规律来回跑动，上下摆杆在垂直平面内左右摆动，以实现摆杆的动态平衡。假设系统中的每一根摆杆都是匀质刚体，则可忽略摆杆运动中的动摩擦。设定小车质量为m,下摆杆质量为M1，上摆杆质量为M2，下摆杆角位移为θ1，上摆杆角位移为θ2，小车与地面的摩擦系数为f,下摆杆长度为L，上、下摆杆转动中心到摆杆中心的距离分别为l1、l2，摆杆按顺时针旋转为正。

图2 二级倒立摆模型Fig.2 Model of double inverted pendulum

2.1 系统建模

倒立摆在平衡位置时，θ1、θ2均取0，通过平衡位置线性化后，可得：

(1)小车运动方程为

(12)

(2)下摆杆运动方程为

(13)

(3)下摆杆运动方程为

(14)

(15)

其中：

2.2 倒立摆系统稳定性分析

倒立摆线性系统稳定性可通过计算系统矩阵A的特征值来判断，如果特征值均处于s复平面的左半平面，则系统稳定。在MATLAB语言中，用函数eig(A)计算矩阵的特征值，经计算得线性定常系统特征值为[-11.829 -5.8745.874 11.829 0 0]T,系统显然不稳定，需设计控制器使其稳定。

要设计最优控制器，首先保证系统是可控的。在MATLAB语言中采用rank(ctrb(A,B))，rank(obsv(A,C))求取系统可控性以及可观性矩阵的秩。经计算，系统可控可观。因此，上述系统可以采用LQG控制器进行控制，使系统闭环稳定。

2.3 LQG/LTR控制器设计

在系统输入端和输出端分别加入外界干扰w(t)和量测噪声v(t)，由于w(t)和v(t)是白噪声信号，可在仿真模块中选择白噪声模块，分别作为模型不确定性和输出噪声。假设这些噪声都是零均值的Gauss过程，则选择Kalman滤波器噪声强度权函数为

Ξ=mI6×6,Θ=nI6×6

(16)

根据式(7)、式(8)，利用MATLAB语言中的care函数求出Pf,再使用inv函数得到卡尔曼滤波器Kf。不断调节m和n,使得卡尔曼滤波器回比函数GkF=C(sI-A)-1Kf的奇异值满足鲁棒性能要求。同时，不断调节状态变量Q、R值，使Gc(s)G(s)奇异值曲线在频率范围内足够逼近卡尔曼回比函数GkF=C(sI-A)-1Kf的奇异值曲线，这样整个系统的性能得到了保证。倒立摆系统仿真结构如图3所示。

2.4 仿真分析

在仿真过程中，初始条件设定为x=[011000]T，LQG/LTR控制效果如图4所示，LQR仿真效果如图5所示。由图4、图5可看出，两种控制方式都较好地跟踪了输入，采用LQG/LTR控制的各性能指标均优于LQR控制。即使有外界干扰和噪声的情况下，小车位移和摆角均在2 s内达到稳定，超调比LQR控制明显降低;LQR控制下的位移和摆角均围绕0值附近范围内波动。由此可以验证，卡尔曼滤波器的引入明显减少了外界干扰和测量噪声对控制系统的影响。

图3 控制系统仿真结构图Fig.3 Simulation structure of control system

(a)小车位移 (b)下摆角角度 (c)上摆角角度

图4LQG/LTR控制效果

Fig.4SimulationresultswithLQG/LRT

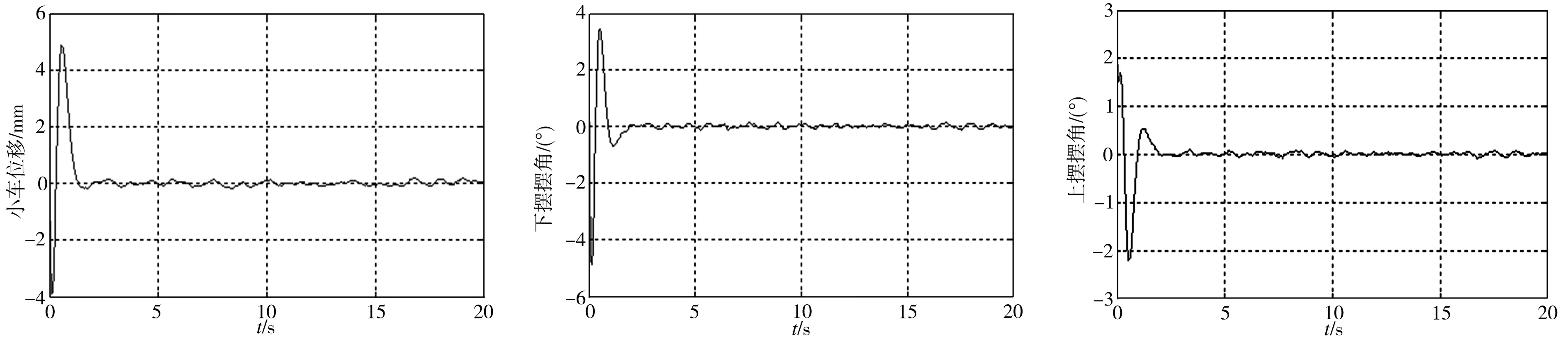
(a)小车位移 (b)下摆角角度 (c)上摆角角度

图5LQR仿真效果

Fig.5SimulationresultswithLQR

3 结语

(1)针对二级倒立摆摆动过程中外界干扰和传感器量测噪声的存在，采用鲁棒控制理论中的LQG/LTR方法设计了带有卡尔曼滤波器全状态反馈的LQG控制器。

(2)对LQG控制器进行回路传输恢复后，得到LQG/LTR控制器，系统能够获得对外界干扰和量测噪声更好的鲁棒性，具有增益欲度无穷大和不少于60°相位欲度，满足了系统控制要求。

(3)将LQG/LTR控制器与LQR控制器进行仿真对比发现，在二级倒立摆系统中LQG/LTR控制器有效解决了在外界干扰和量测噪声等情况下出现的不稳定问题，并具有较好的鲁棒性。

[1] 叶建斌，郭鸿武. 三级倒立摆的LQG最优控制应用研究[J].计算技术与自动化，2011，30(4)：9-13.

[2] 章萌，章卫国，孙勇. 基于闭环准则的LQG/LTR飞行控制律优化设计[J].飞行力学，2011，29(5)：49-53.

[3] 薛定宇. 控制系统计算机辅助设计[M]. 北京:清华大学出版社，2006：314-318.

[4] 王春民，栾卉，杨红应. 倒立摆的设计与仿真[J].吉林大学学报：信息科学版，2009，27(3):242-247.

[5] 吴朔媚，柴忠良，宋宏伟. 基于倒立摆系统的最优控制理论研究[J].煤炭技术，2012，31(5)：198-200.