基于插值组合核的LS-SVR板形预测方法

姚钰鹏，王 京

(北京科技大学冶金工程研究院，北京，100083)

金属板带材广泛应用于家用电器、食品包装、汽车制造以及航空航天等领域，其对板带材的质量如厚度、宽度、板形等精度要求很高，尤其是对板带材的板形质量要求更高[1]。通过预测控制可对板形值进行预报，提前修正控制参数以改善控制器性能，故带材板形值预测控制方法一直是国内外研究的热点。

近年来，在预测板形值的智能算法研究方面，Carlstedt等[2]提出最小二乘法拟合板形识别方法和基于BP神经网络的板形模式识别方法；Nandan[3]、Chakraborti等[4]利用遗传算法对带钢指标综合函数的预测进行了优化；Liu等[5]采用遗传反向传播神经网络来建立板形误差指标和板形控制参数之间的传递矩阵，并将其应用到900 mm HC冷连轧机上；John等[6]用人工神经网络建立输入参数和带钢平直度模型，并利用遗传算法对控制参数进行了优化。但上述研究在智能算法上存在泛化能力一般且寻优容易陷入局部极值的问题，为此李琳等[7]提出支持向量机(SVM)算法是一种基于结构风险最小化学习训练的方法，与上述算法相比具有较好的泛化能力和全局最优性而成为近年来板形控制的研究重点，如陈爱玲等[8]提出利用SVM算法对30MnSi钢变形抗力进行预测；陈治明等[9]提出一种基于混沌优化的支持向量机算法来优化板形预测模型。然而除了参数对SVM算法有影响外，支持向量机的许多特性是由核函数来决定的[10]，为此Steinwart等[11]对多类具有固定形式的核函数进行了研究，Smits等[12]提出了一种将经典核函数进行线性混合得到新的核函数的构造方法；吴涛等[13]提出一种基于Shepard插值的核函数构造方法来增强算法泛化能力。但固定形式的核函数组合依然存在局限性，而Shepard插值仅通过向量欧氏距离倒数作为加权值，还无法反映出数据之间的关联与不确定性。

为此，本文基于RBF核的LS-SVR模型，采用实验变差函数计算插值算法权值，对权系数与各训练样本内积值相乘所反映样本空间结构和相互间关联度的插值核函数进行构造，提出了一种通过Kriging空间散乱插值方法利用样本数据构造出的插值核函数与RBF核函数进行组合而成的核方法，并将其应用于最小二乘支持向量回归机来预测板形值。

1 基于RBF核的LS-SVR算法

基础的支持向量机对于线性可分的训练样本集有较好的分类和回归效果[14]，然而工业现场的很多样本数据是线性不可分的，在线性不可分的情况下存在着一些样本不能被最优分类面正确分类的情况[7]。故训练集为非线性时，可通过某一非线性函数f(·)将训练集数据x映射到一个高维线性特征空间，在这个维数可能为无穷大的线性空间中构造回归估计函数f(x)，即：

f(x)=wφ(x)+b

(1)

式中：w为权矢量，其维数为特征空间维数。

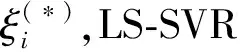
(2)

引入拉格朗日乘子得到对偶最优化问题：

L(w,b,ξ,a)=

b+ξi-yi)

(3)

通过式(3)对各系数偏导为0，可将优化问题转化为求解线性方程：

(4)

式中：K(xi,xj)为核函数；ai为拉格朗日乘子；b为估计修正量；C为惩罚参数，用于控制模型复杂度与训练误差在目标函数中的比重。

通过求解上述线性矩阵问题，得到估计函数系数ai和修正量b，然后代入式(1),从而得到回归预测函数。

核函数方法是在非线性可分的情况下使用非线性变换φ(·)，将输入模式空间中的数据映射到高维特征空间，在其内构造新的分类函数以实现线性可分。核函数形式和参数的变化会隐式地改变输入空间到特征空间的映射，影响支持向量回归性能[12]。核函数从训练与测试性能上划分主要有局部性和全局性两类[10]。RBF核函数是一种常用的经典核函数，通过研究可知其为局部性核函数。图1为当Δ分别取0.1～0.4的四种参数，-0.3为测试输入时RBF核函数的计算结果曲线。由图1可看出，RBF核函数仅在测试点附近小范围内有较大取值，而在范围之外取值都是呈指数性减小。在训练阶段，由于训练数据包括输入参数和实际输出，通过RBF核函数进行已知量回归能较准确找到以式(3)为限定条件的极值点而产生良好的学习效果。但对于测试样本，数据只包含输入参数没有实际输出结果，若测试向量与已有训练向量的欧氏距离较大，则会出现两端数值极小的情况，这也影响了最小二乘支持向量寻优的效果。

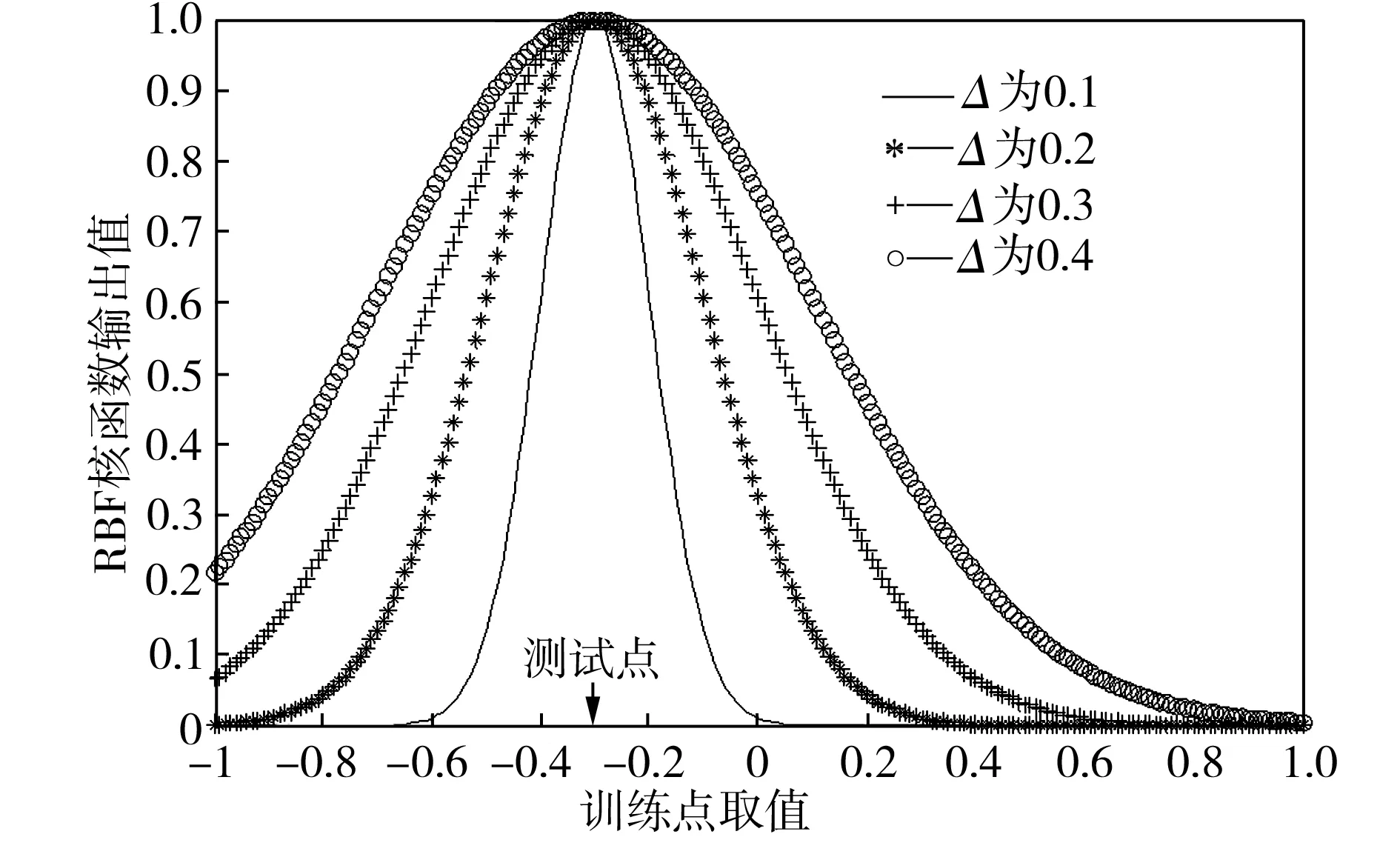
图1 不同宽度参数下RBF核函数的计算结果

Fig.1RBFcalculationresultsatdifferentvaluesofthewidthparameter

由此可知，RBF核函数属于局部性核函数，其在训练过程中有较强的学习能力，但在测试过程中其回归预测的泛化能力较弱。而全局性核函数的特点即使远离测试点的值也有一定的核函数输出，但不同输入的输出间差值较小，学习拟合能力较差。故考虑通过寻找一个全局性核函数与RBF核函数进行组合形成新的核函数来互补全局性和局部性核函数各自弱点，以改善预测性能。

2 基于插值的组合核函数描述

为选取一种全局性核函数，考虑选用Kriging插值方法来构造插值核函数，再将其与RBF核函数形成组合核函数。与传统核函数不同，插值核函数是一种基于训练样本数据得出的核函数映射，它是随训练样本变化而改变的全局性核函数[13]。

2.1 训练样本内积值确定

在支持向量回归算法中，通常所采用的核函数必须满足Mercer条件[15]，其要求通过核函数计算生成的矩阵k=K(xi,xj) (i,j=0,1,…,n)在所有的训练集上半正定。接下来通过下面定理定义内积运算k(x,xi)使对于任意测试样本x，其核函数值构成的gram矩阵是半正定的。

定理[13]设K=(kij)m×m是一个m维的半正定矩阵且满足下列条件：

(5)

若对称函数k(x,xi) 具有如下形式：

(6)

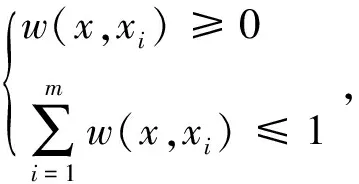
(7)

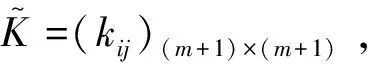
(8)

核函数是样本向量间的一种内积表达，为了实现内积值能反映出样本间区别，可暂时用分类问题的思想来处理回归问题，因二者在训练过程中的寻优算法本质是一样的，区别仅在于它们的决策函数不同与输出的取值范围不同，分类问题的输出只允许取两个值，而回归问题的输出可取任意实数[16]。设最优分类超平面的两边为两类，在特征空间中两边的训练样本属于各自不同的子空间，此时可用向量间的夹角等效于内积值代替欧氏距离来判别样本子空间的归属，定义同类样本向量相互平行，异类样本向量相互垂直，则内积值为

(9)

2.2 Kriging法构造插值核函数

通过选取的训练样本数据可得由内积值k(xi,xj)构建的矩阵K的各元素值，而接下来就需要利用插值的方法估计出训练样本与测试样本间的内积值k(x,xj)。由于训练样本数据是多维且散乱排布的，故选用散乱数据插值中的Kriging插值方法来构造插值核函数。

在空间散乱点插值方法中，简单地用距离倒数作为权值无法反映实际插值曲面的数据分布特性，而Kriging方法通过采用以距离为自变量的实验变差函数来计算权值，由于实验变差函数可以反映变量的空间结构特性和随机分布特性，故该散乱点插值方法可以有较好的估计效果[17]。

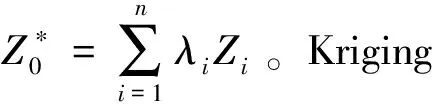
(10)

其对λi的偏导数为

(11)

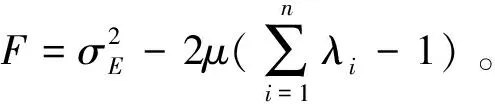
(12)

式中：λi为Kriging方程系数，Cij与Ci0为协方差函数，即：

Cij=E[Z(xi)Z(xj)]-

E[Z(xi)]E[Z(xj)]

(13)

此时为简化算法设训练样本数据满足本征假设，即可得到如下关系：

E[Z(xi)][Z(xj)]

(14)

可得变差函数y(x)为

yij=E[Z(xi)-Z(xj)]2=-2Cij

(15)

此时系数求取方程组为

(16)

而在板形预测样本中数据散乱分布，但不是随机变量，故用改进的实验变差函数代替变差函数，原始实验变差函数为[17]

Z(xi+h)]2

(17)

式中：hij为偏差向量；N(hij)为偏差向量总数。

由于训练样本维数较多，几乎每组样本都不相同而导致偏差向量数量较多、计算量较大。又因为实验变差函数是样本间关联程度的一种表示，设轧制参数生成的时间差为一个关联程度指标，通过将样本生成时间差tij代替hij得到改进实验变差函数：

(18)

式中：tmax为最后一个样本的生成时间点(初始时间为0)。

通过训练样本中已知的核函数数据可得到改进实验变差函数值r(tij)代替变差函数y(h)，得到新的求加权系数的方程组：

(19)

进而解出各加权系数λi(i=1，2，…，n)得到改进的插值核函数构造方法：

(20)

式中：k(xi,xj)为已提到的只有0、1二值的简化内积值；n为训练样本数量。

2.3 组合核函数

由于插值构造核函数的方法可实现远离测试输入点的样本数据对核函数的值有影响，属于全局性核函数，其泛化能力强但学习能力较弱[13]。而由图1可知，径向基核函数是局部性核函数，其形式为

(21)

式中：σ为其宽度参数。σ越小,核函数的学习能力越强，但会加大计算难度。而σ的选取不当可能会导致核函数学习能力大幅下降，即局部性影响加强，损失了泛化能力。因此将基于训练样本数据的插值核函数与有固定形式的传统核函数进行组合，通过选取一个局部核函数来与插值核函数进行互补，以优化数据回归预测的性能。

对两类核函数进行组合的实质就是在同样的训练样本和测试样本进行回归预测条件下，分别计算出两类核函数的取值，然后通过加权线性组合的方法将每个测试样本核函数值进行计算，得出一组与测试样本同数量的结果即为组合核函数的取值。其组合形式为

KSUM=ωK0+(1-ω)KRBF

(22)

式中：ω为组合核函数的分配系数，在仿真实验中通过等步长搜索方法对其进行寻优。

3 仿真实验与结果分析

实验数据取自某热连轧项目，在数据采集系统存储的限制下经过初步的机理分析，可作为训练样本的参数有F1～F4机架轧制力、F1～F4机架间的三个张力值、F1～F4机架段轧制速度、F1～F4机架弯辊力和板形凸度实际值共16个指标，而除去实际凸度值，其余指标数据可作为测试样本数据。故训练样本矩阵为一定数量的16维向量所组成的数据矩阵，测试样本矩阵为15维矩阵。为了避免铝带轧制初始与结束阶段的扰动影响，实验选取了某厂热连轧精轧a道次的2.583～3.083 min共3000个样本作为训练样本，其数据表达为3000×16的矩阵；a道次3.583～3.808 min共1350个样本作为测试样本A；b道次3.0～3.225 min共1350个样本作为测试样本B；b道次的2.667～2.892 min共1350个样本作为测试样本C，三个测试样本数据表达均为1350×15的矩阵。

3.1 实验1

首先测试算法的预测效果。由于带材同一位置上凸度的影响因素发生时间不同，本实验对样本数据进行了时序初始化，保持出口侧数据不变，对样本数据进行时间轴不变而数据相对后移的时序调整，依照精轧入口到F1再到F4的顺序减小调整量。本文通过数据采集系统反馈的入口侧、四个机架和出口侧的各自相邻距离与它们间的带材轧制速度相除得到相邻时间修正分量：

(23)

式中：Δti,i-1为相邻时间修正分量；Si,i-1为入口侧、各机架间、出口侧之间的相邻距离；下标值中，“i-1=0”表示入口侧，“1～4”为F1～F4的四个精轧机架，“i=5”表示出口侧；vi(T)为T时刻的带材轧制速度值。

在得到相邻时间修正量后，将其按式(24)进行累加得到入口侧的时序调整量ΔT0和四个机架的时序调整量ΔT1～ΔT4，从而完成时序初始化工作。即：

(24)

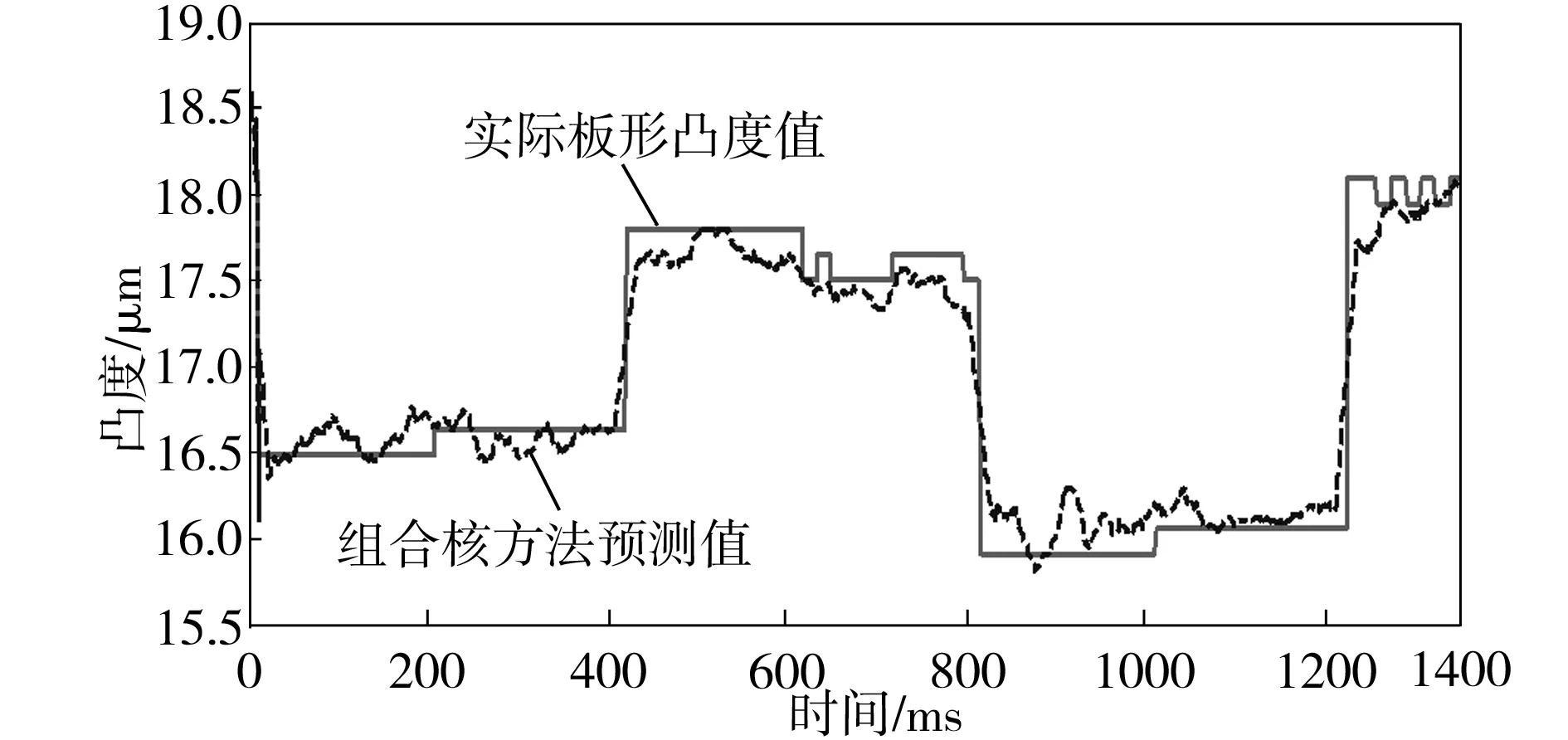
本组实验选取测试样本A作为测试数据，通过算法仿真来比较单RBF方法与组合核方法的预测结果。图2为单RBF方法与组合核方法预测结果的对比。

(b)组合核方法

Fig.2PredictionsbythemethodofRBFandthatofmixturesofkernels

通过交叉验证寻优，本组实验中惩罚因子C取2000，RBF核宽度σ取6，核分配系数ω取0.3。由图2可看出，由于局部性核函数泛化能力较弱，在单RBF核函数下的回归预测结果能勉强跟上实际板形值，但整体结果有较大幅值的高频振荡，无法为现场轧制过程提供有效预测修正；而在基于组合核函数的回归预测中，估计结果较好地跟踪上了实际板形值，其预测趋势正确且振荡幅值不大，可以保证预测结果有能力对现场轧制的参数有一定的预测修正作用。

本组实验对两种方法的训练样本自回归和测试样本回归的各项性能指标进行了对比，从而考察组合核方法的学习能力和测试能力。表1为基于不同核函数回归算法的学习训练性能对比。由表1可看出，基于组合核的训练效果相比于RBF核函数有一定提升，其误差小于3%的数据命中率有4.72%的提升，其相对误差减小的程度为0.13%，误差控制效果提升不大；基于组合核的回归方法较于基于单RBF核的回归方法训练能力有小幅改善。

表2为基于不同核函数的回归算法的测试性能对比。由表2可看出，基于组合核算法较于基于单RBF核算法在误差小于3%的数据命中率有21.11%的提升，相对误差减小的程度为1.06%，测试误差控制效果有一定提升。由此看出，基于组合核的回归算法较于基于单RBF核的回归算法在测试性能上有一定改善。

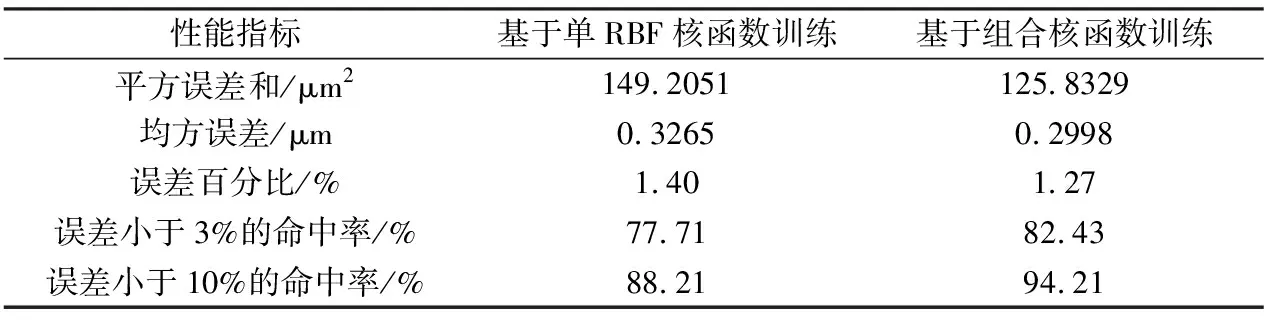
表1 不同核函数选取下的学习训练性能指标Table 1 Performance indexes of learning and training with different kernels

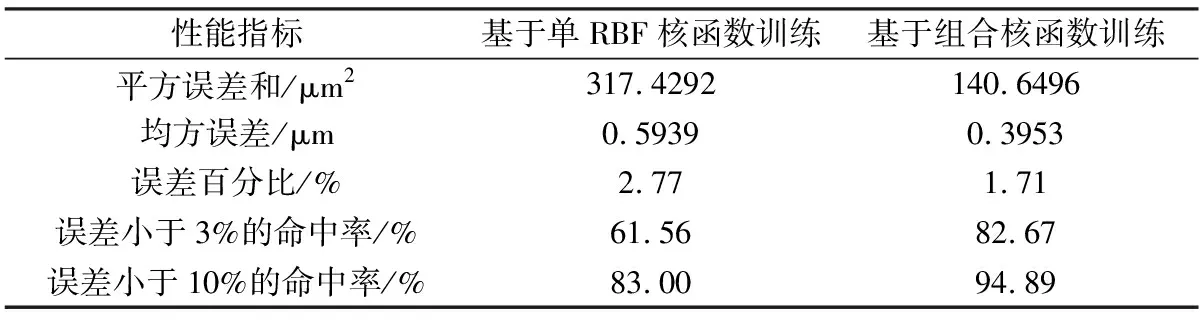
表2 不同核函数选取下的回归测试性能指标Table 2 Performance indexes of regression testing with different kernels

3.2 实验2

对于支持向量回归算法，除了保证当前道次板形回归预测的准确度，还需要对泛化能力提出要求。只有泛化能力良好的回归预测算法才能有效地应用于板形值估计，故其是本研究的一项重要衡量指标。

通过在相同样本数据进行学习训练的情况下，选取包括与样本数据在同一卷和不同卷铝带的数据作为测试样本，用不同卷铝带预测相对误差值与同卷铝带预测相对误差值作差法得到的偏差值来表示基于不同核函数的回归算法泛化能力，其数学表达式为

(25)

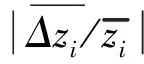
本组实验选取实验1的训练样本，选取测试样本A和与其不同道次的测试样本B(板形波动较小)、测试样本C(板形波动较大)的轧制参数作为测试样本集。在基于不同核函数的支持向量回归算法下观察各组相对误差偏差值，得出两种算法的泛化能力对比结果如表3所示。

表3 基于不同核函数回归算法的泛化能力对比Table 3 Generalization abilities of regression algorithms based on different kernels

本组实验参数选取同实验1。由表3可看出，基于组合核函数的支持向量回归算法对与训练样本不同道次的测试样本测试误差增加量小于基于单RBF核函数的回归算法的误差增加量。不难看出，基于新核函数的回归算法的泛化能力有一定提高。

4 结语

(1)针对热连轧板形测量滞后而影响板形控制效果的问题，提出了一种基于样本数据的插值方法来构造非固定形式的核函数，并将其与经典的RBF核函数进行线性组合得到新的组合核函数应用到板形预测中。

(2)由于板形训练样本维数多且散乱分布，故在插值算法的选取上采用了可完成空间散乱插值的Kriging插值方法。实验表明，通过Kriging插值方法构造基于数据的核函数对局部性的RBF核函数有较好的全局性补充，其二者组合可应用于支持向量回归。

(3)通过与传统RBF方法的比较，本方法在学习训练性能上较为接近；测试性能上有所改善，均方误差减小，预测命中率提高；泛化能力有所增强，板形预测精确度有了一定程度的提高，为基础自动化的板形预测控制系统提供了良好的先验信息。

[1] 孙一康．带钢热连轧的模型与控制[M].北京：冶金工业出版社，2002：164-168．

[2] Carlstedt A G, Keijser O. Modern approach to flat-nessmeasurementandcontrolincoldrolling[J].Iron and Steel Engineer, 1991, 68(1): 34-37.

[3] Nandan R, Rai R, Jayakanth R, et al. Regulating crown and flatness during hot rolling: a multi objective optimization study using genetic algorithms[J]. Materials and Manufacturing Processes, 2005, 20(3): 459-478.

[4] Chakraborti N, Kumar B S, Babu V S, et al. Optimizing surface profiles during hot rolling: a genetic algorithms based multi-objective optimization[J]. Computational Materials Science, 2006, 37(1/2): 159-165.

[5] LiuHongmin,ZhangXiuling,WangYingrui.Tran-sfer matrix method of flatness control for strip mills[J]. Journal of Materials Processing Technology, 2005,166(2): 237-242.

[6] John S, Sikdar S, Swamy P K, et al. Hybrid neural-GA model to predict and minimise flatness value of hot rolled strips[J]. Journal of Materials Processing Technology, 2008, 195(1): 314-320.

[7] 李琳，张晓龙．支持向量机学习方法的选择与应用[J]．武汉科技大学学报：自然科学版，2006，29(1)： 75-78．

[8] 陈爱玲，杨根科，吴智铭．一种混合模型在30MnSi钢变形抗力预测中的应用[J]．上海交通大学学报， 2006，40(10)：1723-1726．

[9] 陈治明, 黄晓红, 罗飞, 等. 基于混沌优化支持向量机的板形预测与优化[J]. 华南理工大学学报, 2009, 37(10): 55-59.

[10]邬啸，魏延，吴瑕．基于混合核函数的支持向量机[J]．重庆理工大学学报：自然科学版，2011，25(10)： 66．

[11]Steinwart I. On the influence of the kernel on the consistency of support vector machines[J]. The Journal of Machine Learning Research, 2002(2): 67-93.

[12]Smits G F, Jordaan E M. Improved SVM regression using mixtures of kernels[C]//Neural Networks.IJCNN’02. Proceedings of the 2002 International Joint Conference on IEEE, 2002: 2785-2790.

[13]吴涛，贺汉根，贺明科．基于插值的核函数构造[J]．计算机学报，2003，26(8)：990-996．

[14]蒋刚．核函数理论与信号处理[M]．北京：科学出版社，2013：4-24.

[15]Vapnik V, Chapelle O. Bounds on error expectation for support vector machines[J]. Neural Computation, 2000, 12(9): 2013-2036.

[16]Vapnik V N. The nature of statistical learning theory[M]. New York: Spring-Verlag, 1998: 181-225.

[17]王靖波，潘懋，张绪定．基于Kriging方法的空间散乱点插值[J]．计算机辅助设计与图形学学报，1999， 11(6)：525-529．