斜齿轮齿向修形对承载能力的影响

杨 柯，李友荣，曾义斌，张伊波

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081;2.武汉钢铁股份有限公司设备维修总厂，湖北 武汉，430083)

某钢厂1580热连轧机主传动系统采用斜齿轮传动方式，该齿轮由于尺寸大、承受重载、工作环境恶劣、不间断工作时间长等因素的影响，曾出现齿面划伤甚至断齿的事故，严重影响轧机的正常生产。为提高齿轮承载能力，保证轧机安全稳定运行，有必要对斜齿轮副进行强度分析。本文以该热连轧机F1轧机主减速机斜齿轮副为研究对象，建立其三维模型，利用有限元软件分析计算齿轮的应力分布情况，并进行强度校核，找出故障产生的原因，结合齿轮齿向修形理论提出最佳修形方案，以期减少齿轮在接触状态下的应力集中，提高减速机斜齿轮传动的承载能力。

1 斜齿轮参数化模型

斜齿轮属于标准件，当法面模数、齿数和螺旋角已知时，其他各几何尺寸可以通过几何关系计算而得。

表1所示为斜齿轮的基本参数。根据表1参数，在Pro/E中通过输入方程添加关系的方式会自动生成齿轮其他部分的相应尺寸[1]，最终得到无干涉齿轮的装配模型，如图1所示。将得到的模型保存为IGS格式，即可导入到有限元程序中进行仿真分析。

表1 斜齿轮副基本参数Table 1 Basic parameters of the helical gear

图1 齿轮装配图Fig.1 Assembly drawing of gears

2 齿轮有限元仿真分析

2.1 定义材料属性

大小齿轮的材料均为17Cr2Ni2Mo，齿面采用渗碳淬火处理，硬度为56～61HRC，泊松比μ=0.3，弹性模量E=207 GPa。

2.2 网格划分

采用自由网格划分,小齿轮的单元尺度设置为50 mm,大齿轮的单元尺度设置为100 mm。为了保证得到的结果更为准确，对局部网格进行细化，即选取齿轮啮合过程中可能会接触的面，设置其单元尺度为10 mm。摩擦系数取为0.1。

2.3 添加约束和载荷

(1)约束。大齿轮轴输出端全约束，输入端只能绕轴向转动。小齿轮轴径向和水平方向约束，使其只能绕轴向转动。

(2)载荷。在小齿轮输入端施加一个逆时针方向的扭矩，其值取为该减速机的额定输入扭矩T=424.44 kN·m。

2.4 子模型分析计算

由于该齿轮副整体结构尺寸很大，在较小的网格密度下计算机计算效率低，较大的网格密度下得到的结果又不够精确，故采用子模型分析方法，将轮齿啮合区从整体模型中切割出来重新计算。子模型纵向宽度取原模型整个齿宽，径向取与内孔距离为1.8倍端面模数的范围。子模型方法又称为切割边界位移法，整体模型切割边界的计算位移值即为子模型的边界条件[2]。子模型单元尺度设为10 mm，轮齿接触面单元尺度设为2 mm。以下数据皆为子模型的精确计算值。

2.5 仿真结果与分析

因齿轮副中小齿轮的应力比大齿轮大，故以下仅讨论小齿轮的应力及强度。在啮合过程中接触中心带是沿一条平行于齿轮轴的直线移动的。因此，为得到斜齿轮在传动过程中不同接触位置的应力值，选取一对啮合齿在其接触带中心分别位于Z=0 mm(Z为齿宽方向坐标，Z=0 mm处即为齿轮端面)、Z=175 mm(1/4齿宽处)和Z=350 mm(齿宽中心处)时的斜齿轮模型进行接触分析。

接触带中心位于Z=0 mm时，小齿轮的第一、第三主应力分布云图以及接触云图分别如图2～图4所示。由图2和图3中可以看出，此时小齿轮最大应力部位在其端部齿根处，该处第一主应力最大值为384.56MPa,第三主应力值为21.4 MPa，处于三向受拉应力状态，应按第一主应力进行强度校核。由图4可知齿面最大接触应力为847.23 MPa。

图2 Z=0 mm时小齿轮的第一主应力分布云图

Fig.2FirstprincipalstressdistributionnephogramatZ=0mmofthepinion

图3 Z=0 mm时小齿轮的第三主应力分布云图

Fig.3ThirdprincipalstressdistributionnephogramatZ=0mmofthepinion

图4 Z=0 mm时小齿轮的接触应力云图

Fig.4ContactstressnephogramatZ=0mmofthepinion

同样可得接触带中心位于Z=175 mm和Z=350 mm时的相应应力值，如表2所示。

表2不同接触带中心位置下齿轮的最大应力值

Table2Maximumstressvalueunderthreedifferentcontactcentersofthegear

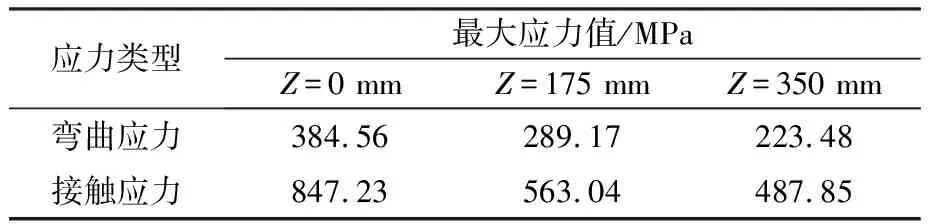
应力类型最大应力值/MPaZ=0 mmZ=175 mmZ=350 mm弯曲应力384.56289.17223.48接触应力847.23563.04487.85

从表2中可见，在轮齿刚进入啮合位置，即Z=0 mm时，齿轮的接触应力和弯曲应力过大，经计算，该齿轮的接触应力安全系数为1.33，大于最小接触应力安全系数SHmin=1.0[3]，满足要求，但弯曲应力安全系数为1.21，小于最小弯曲安全系数SFmin=1.25[3]，不满足要求，因而造成齿轮的损伤，严重时发生轮齿端部断裂(见图5)。因此有必要降低接触带中心位于Z=0mm时齿轮的应力值。本文拟采用齿向修形的方法[4]来降低轮齿端部的应力，以提高齿轮的承载能力。

图5 轮齿断裂形貌Fig.5 Fracture morphology of the gear tooth

3 齿向修形后齿轮的仿真结果分析

3.1 齿向修形方法

齿轮齿向修形主要是对齿轮齿面沿齿向方向进行微量的修整[5]，使其偏离理论齿面，以改善载荷沿轮齿接触线的不均匀分布现象，从而大大提高齿轮的承载能力。考虑到实际应用中加工难度和成本因素的影响，本文采用一种简单的、便于实际运用的齿端修形方法，如图6所示。

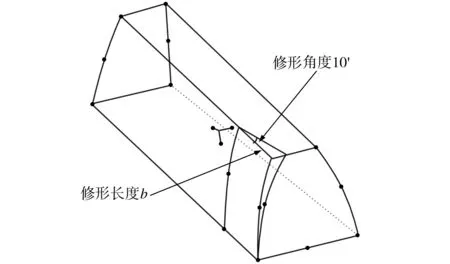
图6 齿向修形示意图Fig.6 Schematic diagram of modification

3.2 接触应力分析

依据图6建立相应的修形齿轮模型，导入到有限元软件中进行分析。设置齿向修形长度分别为60、70、80 mm,每种修形量下取接触带中心位于Z=0 mm、Z=175 mm和Z=350 mm 时的齿轮应力分布云图进行分析。

图7所示为接触带中心位于Z=0 mm时，不同修形量下齿轮的接触应力分布图。由图7中即可得Z=0 mm时不同修形长度下齿面的最大接触应力值。采用同样方法，也可获得Z=175 mm和Z=350 mm时的相应值，结果如表3所示。

由表3中数据计算可得，与修形前相比，随着修形长度的增加，齿面最大接触应力在Z=0 mm和Z=175 mm时都有不同程度的降低，而在Z=350mm时其值变化不大。修形长度分别为60、70、80 mm，Z=0 mm 时齿面最大接触应力比修形前的相应值分别降低了21.38%、27.38%和29.30%；而Z=175mm时相应的降幅分别为3.36%、5.72%和9.52%，明显低于Z=0 mm时的降幅。

表3不同修形量及接触带中心位置下齿面的最大接触应力

Table3Maximumcontactstressatdifferentmeshingpositions

b/mm最大接触应力/MPaZ=0 mmZ=175 mmZ=350 mm0847.23563.04487.8560666.07544.87497.4570615.24531.61503.0180598.96510.16495.29

(a)b=60 mm

(b)b=70 mm

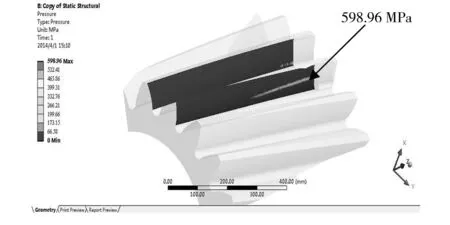
(c)b=80 mm

图7Z=0mm时不同修形长度下齿面的接触应力云图

Fig.7ContactstressdistributionnephogramofthepinionatZ=0mm

3.3 弯曲应力分析

图8所示为接触带中心位于Z=0 mm时，不同齿向修形长度下修形后齿轮的弯曲应力分布图。

将图8与图3对比可以发现，齿向修形后，齿轮弯曲应力最大值区域偏离齿根端部一定距离，显著地降低了齿根端部的应力值，可避免由于齿根端部应力值过大而产生的轮齿断裂[6]。采用同样方法可得Z=175 mm和Z=350 mm时齿根的最大弯曲应力。取3种修形量下接触带中心位于不同位置时齿根的最大弯曲应力值列于表4。

由表4中可见，与未修形时相比，不同修形长度下修形后齿根最大弯曲应力在接触带中心位于Z=0 mm和Z=175 mm时有着不同程度的变化，而位于Z=350 mm时却变化不大，修形 长度为60、70、80mm时,Z=0mm时其降幅分别为16.85%、21.66%和22.40%；Z=175 mm时其降幅分别为8.6%、11.01%和12.75%。

(a)b=60 mm

(b)b=70 mm

(c)b=80 mm

图8Z=0mm时不同修形长度下修形后齿轮的弯曲应力云图

Fig.8BendingstressnephogramofthegearatZ=0mm

表4不同修形量及接触带中心位置下齿根的最大弯曲应力

Table 4 Maximum bending stress of root at different locations

3.4 最佳修行量的确定

综上分析可知，齿向修形长度量为80 mm时，齿面最大接触应力和齿根最大弯曲应力降幅最大，改善齿轮承载能力的效果最明显，故理论上最佳修行量应为80 mm,但在实际生产中，要在减速机斜齿轮上修形80 mm，其费用要比修形70 mm时高很多，而这两种修形量下齿轮所受应力的降幅相近，修形70 mm时已经能够满足要求。综合考虑，选取70 mm为实际最佳齿向修形长度。

4 结论

(1)斜齿轮在刚进入啮合的时候，其齿面接触应力和齿根弯曲应力值过大，是造成轮齿划伤、磨损甚至断裂的主要原因。

(2)齿向修形能够在很大程度上降低齿轮啮合过程中的最大应力值，明显提高齿轮的承载能力。

(3)某钢厂1580热连轧机主减速机最佳齿向修形长度确定为70 mm，不但能够满足提高齿轮承载能力的要求，而且降低了加工成本。

[1] 杨生华.齿轮接触有限元分析[J].计算力学学报，2003, 20(2)：189-194.

[2] 田涌涛,李从心,佟维，等.基于子结构技术的复杂齿轮系统有限元三维接触分析[J].机械工程学报, 2002,38(5):133-137.

[3] 吴宗泽.机械设计师手册(上册)[M]. 北京: 机械工业出版社, 2002.

[4] 潘洪鑫.齿轮修形技术研究[J].中国新技术新产品，2011(13):122.

[5] 吕少炯.渐开线圆柱齿轮修形及其对传动性能影响的研究[D]. 南京:南京航空航天大学，2010.

[6] Giorgio Bonori,Marco Barbieri,Francesco Pellicano.Optimum profile modifications of spur gears by means of genetic algorithms[J].Journal of Sound and Vibration, 2008, 313(3-5): 603-616．