基于统计学的葡萄酒评价数学模型
陈 锦
(广西师范大学 电子工程学院,广西 桂林 541004)
随着人们生活水平的提高,葡萄酒的质量需求也相应的增加,因此葡萄酒的认证和质量评价也得到关注。对葡萄酒的质量评价,需要深入分析酿酒葡萄的理化指标、葡萄酒的理化指标、葡萄酒的质量之间的联系。因此本文根据三者的联系建立了葡萄酒质量评价的多元线性回归模型。
1 葡萄酒评分员对葡萄酒评价分析模型
1.1 两组评酒员评价结果的显著性差异分析
在实际葡萄酒质量的评价中,我们会选择多组评酒员对葡萄酒样品进行评价,因此我们需要对多组评酒员结果的显著性差异的分析。本文介绍t检验、F检验、秩和检验[1-2]3种显著性差异分析模型。
(1)t检验

(2)F检验

(3) 秩和检验
将观察值由小到大排列,得到序列号,即秩次。再将秩次代替原始数据按要求进行秩和检验。
设μA,μB,分别为两组葡萄酒评分的均值,在水准α=0.05下检验假设:H0∶μA=μB,H1∶μA≠μB,h为检验结果。h=0表示A与B的总体差别不显著;h=1表示A与B的总体差别显著[3]。
1.2 两组评酒员评分可信度模型
葡萄酒有外观分析,香气分析,口感分析,平衡整体分析4个评分项目,将评酒员在不同评分项目的评分求和,每个项目总评分,求其方差:δ1,δ2,δ3,δ4。我们定义一个评价指标:
(1)
评价指标η的值越小,评价结果越可信。
2 酿酒葡萄分级模型
酿酒葡萄的质量直接影响葡萄酒的质量,因此我们通过葡萄酒的质量可以分析酿酒葡萄的质量,分析酿酒葡萄的质量我们还可以通过酿酒葡萄本身的理化指标进行分析,所以我们通过酿酒葡萄的理化指标和葡萄酒的质量对酿酒葡萄进行分级。
研究中我们采用了因子分析的方法,因子分析是一种比较好的分类方法,本文还建立了一种统计分级模型对酿酒葡萄进行分类。
2.1 因子分析模型
把酿酒葡萄的一级理化指标作为一个公共因子,显然酿酒葡萄的质量是由葡萄的所有一级理化指标来确定的,第i个酿酒葡萄的质量为Zi,理化指标为Fi。以主成分分析的统计方法分析影响葡萄品质的主成分,通过相关性分析和聚类分析对影响葡萄品质的指标进行研究,筛选出能够客观反映出葡萄品质的简化指标,为快速,准确的判断葡萄品质打下基础[4]。
Zi=ai1F1+ai2F2+…+aimFm+ui+
bui(i=1,2,…,n)
(2)

2.2 统计分级模型
设置信区间为Ai=[ai,j,ai,j],第i等级i=1,2,3,…,n,第j个理化指标j=1,2,3,…,m。定义一个覆盖率为β,
(3)
我们规定,当β满足一定条件我们可求得样品葡萄质量的分类标准。
本文的实验数据来源于2012年全国大学生数学建模竞赛A题葡萄酒评价,根据建立的因子分析模型和统计分级模型,通过MATLAB软件计算得出酿酒葡萄主要影响理化指标见表1和酿酒葡萄的分级结果见表2、3。
3 多元回归分析模型分析酿酒葡萄与葡萄酒理化指标的联系
研究分析葡萄酒质量只和部分指标的关联较大,所以我们去掉一些关联不大的指标。用关联较大的指标来表示出葡萄酒的质量。
表1酿酒葡萄主要影响理化指标
Table1Winegrapemainlyaffectphysicalandchemicalindicators

葡萄种类酿酒葡萄主要影响理化指标红葡萄氨基酸总量,蛋白质,VC含量,花色苷,酒石酸,苹果酸,柠檬酸总酚,白藜芦醇白葡萄氨基酸总量,蛋白质,VC含量,花色苷,酒石酸,苹果酸,柠檬酸多酚氧化酶活力,总酚,黄酮醇,总糖,PH值
表2红葡萄的分级
Table2Classificationofredgrapes
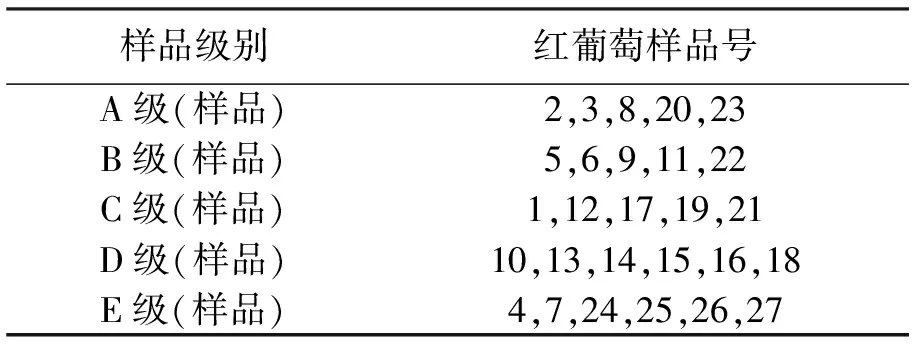
样品级别红葡萄样品号A级(样品)2,3,8,20,23B级(样品)5,6,9,11,22C级(样品)1,12,17,19,21D级(样品)10,13,14,15,16,18E级(样品)4,7,24,25,26,27
表3白葡萄的分级
Table3Classificationofwhitegrapes

样品级别白葡萄样品号A级(样品)3,11,16,23,27B级(样品)9,10,13,17,24C级(样品)1,2,8,19,22,25D级(样品)6,14,20,21,26,28E级(样品)4,5,7,12,15,18
3.1 多元线性回归模型
影响葡萄酒样品理化指标的因素往往不止一个,即多个葡萄理化指标,假设它们之间有如下的线性关系式:
y=β0+β1x1+…+βkxk+ε
(4)
其中y为可观察的随机变量,称为因变量为非随机的精确观察的变量x1,x2,…,xk,称为自变量或因子,β0,β1,β2,…βk为k+1个未知参数,ε是随机变量,一般假设Eε=0,Dε=σ2>0。
多元线性模型和回归系数的检验[5-6]:
(5)
在实际问题中,事先我们并不知道或者不能断定随机变量y与一组变量x1,x2,…xk之间确有线性关系y=β0+β1x1+…+βkxk+ε往往只是一种假设,因此在求线性回归方程之后,还须对求出的线性回归方程同实际的观测数据拟合效果进行检验,可提出以下原假设
H0∶β0=β1=β2=…=βk=0
(6)
r检验法:与一元回归情形类似,y与x1,x2,…,xk线性相关的密切程度也可用回归平方和U在总平方和Lyy中所占的比例大小来衡量,定义
(7)
为y与x1,x2,…,xk的多元相关系数或复相关系数。容易证明F与R有如下关系:
(8)
3.2 典型相关分析模型
典型相关分析是研究两组变量之间的相关关系的一种多元统计方法。典型相关分析首先在每一组变量的线性组合,使其具有最大相关性,然后再在每一组变量中找出第2对线性组合,使其与第1对线性组合不相关,而第2对本身具有最大相关性,如此继续下去,直到两组变量之间的相关性被提取完毕为止,这些综合变量称为典型变量[7]。

典型相关分析用X和Y的线性组合U=αTX,V=bT之间的相关来研究X和Y之间的相关性。其目的就是希望找到向量a和b,使ρ(U,V)最大,从而找到替代原始变量的典型变量U、V[8]。
典型相关系数的数学定义为:
(9)
由于随机变量乘以常数不该变其相关系数,为防止不必要的结果重复出现,最好在其附加如下约束条件:
Var(U)=αT∑11a=1
Var(V)=αT∑22b=1
(10)

对2012年全国大学生数学建模竞赛A题葡萄酒评价实验数据进行MATLAB仿真计算可得线性回归多项式:
(11)
葡萄酒的理化指标为ωi,i=1,2,…9,葡萄的理化指标为gj,j=1,2,…9,则
ωi=bi0+bi1g1+bi2g2+…+bi13g13
以一个wi作为示例:
w1=200.36-0.01g2+2.71g3+2.29g4-
2.42g5+4.42g6+2.84g7+0.39g8-1.27g9+
0.52g10+0.62g11+0.04g12-45.49g13
由式11可以计算得出,白(红)葡萄与白(红)葡萄酒的理化指标的多项式系数见表4、表5。
表4白葡萄与白葡萄酒的理化指标的多项式系数
Table4Whitegrapesandwhitewinephysicalandchemicalindicatorsofthepolynomialcoefficients
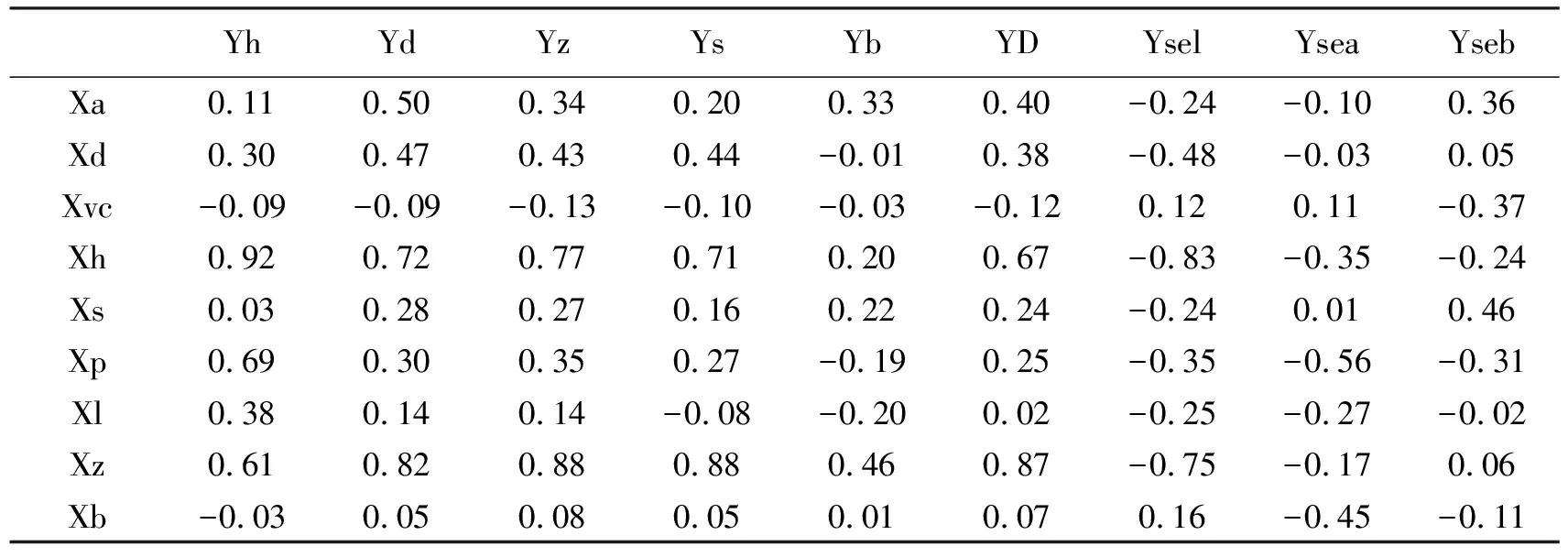
YhYdYzYsYbYDYselYseaYsebXa0.11 0.50 0.34 0.20 0.33 0.40 -0.24 -0.10 0.36 Xd0.30 0.47 0.43 0.44 -0.01 0.38 -0.48 -0.03 0.05 Xvc-0.09 -0.09 -0.13 -0.10 -0.03 -0.12 0.12 0.11 -0.37 Xh0.92 0.72 0.77 0.71 0.20 0.67 -0.83 -0.35 -0.24 Xs0.03 0.28 0.27 0.16 0.22 0.24 -0.24 0.01 0.46 Xp0.69 0.30 0.35 0.27 -0.19 0.25 -0.35 -0.56 -0.31 Xl0.38 0.14 0.14 -0.08 -0.20 0.02 -0.25 -0.27 -0.02 Xz0.61 0.82 0.88 0.88 0.46 0.87 -0.75 -0.17 0.06 Xb-0.03 0.05 0.08 0.05 0.01 0.07 0.16 -0.45 -0.11
注:Xa—Xb:氨基酸总量、蛋白质、VC含量、花色苷、酒石酸、苹果酸、柠檬酸、总酚、白藜芦醇;
Yh—Yseb:花色苷、单宁、总酚、酒总黄酮、白藜芦醇、DPPH半抑制体积(IV50) 1/IV50、色泽L*(D65)、色泽L*(D66)、色泽L*(D67)。
表5红葡萄与红葡萄酒的理化指标的多项式系数
Table5Redgrapesandredwinephysicalandchemicalindicatorsofthepolynomialcoefficients

YhYdYzYsYbYDYselYseaYsebXa0.00 0.43 0.48 0.29 -0.22 0.21 -0.41 0.08 0.28 Xd0.00 0.36 0.42 0.60 -0.22 0.23 0.08 0.45 -0.13 Xvc0.00 -0.17 -0.10 -0.16 0.13 0.23 0.22 -0.09 -0.10 Xh0.00 -0.22 -0.30 -0.16 0.07 -0.18 -0.08 -0.12 0.07 Xs0.00 0.18 0.00 -0.19 -0.31 0.10 -0.25 -0.30 0.31 Xp0.00 0.05 0.12 0.47 -0.25 -0.12 0.10 0.38 -0.27 Xl0.00 0.25 0.08 0.16 -0.10 -0.05 -0.08 -0.23 0.16 Xdf0.00 -0.24 -0.40 -0.23 0.16 -0.37 0.01 -0.02 -0.05 Xz0.00 0.43 0.55 0.74 -0.14 0.42 0.12 0.40 -0.20 Xht0.00 0.41 0.39 0.61 -0.09 0.36 -0.20 0.00 0.24 Xzt0.00 0.36 0.32 -0.13 -0.37 0.24 -0.55 -0.21 0.54 Xph0.00 0.17 0.12 -0.17 -0.05 0.05 -0.28 -0.29 0.34
注:Xa-Xph氨基酸总量、蛋白质、VC含量、花色苷、酒石酸、苹果酸、柠檬酸多酚氧化酶活力、总酚、黄酮醇、总糖、PH值;
Yh-Yseb:花色苷、单宁、总酚、酒总黄酮、白藜芦醇、DPPH半抑制体积(IV50) 1/IV50、色泽L*(D65)、色泽L*(D66)、色泽L*(D67)。
根据表4、表5相关系数建立的多项式,分析葡萄酒与葡萄的理化指标之间的关系,由红葡萄与红葡萄酒理化指标的相关系数表格分析可知,红葡萄酒的花色苷理化指标主要由红葡萄的花色苷决定的,总酚由红葡萄的总酚决定,红葡萄酒的酒总黄酮主要来自于红葡萄的总酚,红葡萄酒的色泽主要由红葡萄的蛋白质、花色苷、苹果酸影响的。通过白葡萄与白葡萄酒理化指标的相关系数表格分析可知,白葡萄酒的花色苷不是来自白葡萄的,白葡萄酒的单宁主要由白葡萄里的氨基酸、总酚、黄酮酸决定,白葡萄酒的总酚主要来自于白葡萄,白葡萄酒里的酒总黄铜与白葡萄的蛋白质、黄酮酸相关,白葡萄酒得色泽主要由白葡萄里的总糖、苹果酸决定。
4 结束语
本文建立了多元线性回归模型,详细研究了葡萄酒的评价、酿酒葡萄的分解以及葡萄酒与酿酒葡萄直接的联系与影响。该模型可以推广到食品产业对食品质量检测分析中,为提高食品生产质量和食品质量检测精度提供了很好的方案。
参考文献:
[1] 王松桂.概率论与数理统计[M].北京:科学出版社,2011.
[2] 邓薇.MTLAB函数速查手册[M].北京:人民邮电出版社,2012.
[3] 谢辉.统计方法在葡萄理化指标简化中的应用[J].新疆农业科学,2011,12(14):25-36.
[4] 聂继云.白梨品质评价指标的聚类分析[J].中国果树,2000,2(25):68-69.
[5] 张英莉.新疆天山北麓地区赤霞珠干红葡萄酒香气成分的分析[J].中外葡萄与葡萄酒,2011,24(14):225-227.
[6] 张凤菊.数据差异显著性检验[J].农机使用与维修,2012,4(5):26-30.
[7] 王金甲.基于物理化学性质的葡萄酒质量的可视化评价研究[J].燕山大学学报,2011,3(4):124-128.
[8] 张路.典型相关分析应用常见分析及处理[J].沈阳体育学院学报,2010,30(5):12-18.

