基于矩阵模式的局部子域最大间距判别分析

黄丽莉

(1.安徽理工大学 电气与信息工程学院，安徽 淮南 232001; 2.盐城工学院 信息学院，江苏 盐城 224051)

智能识别领域存在着大量需要处理的高维数据样本，为了便于从中找出我们最需要的信息，就需要进行特征降维，将一些冗余的信息进行处理。特征提取作为一种数据预处理方法得到了广泛的运用[1]。一般经典的特征提取方法，如：PCA[2,3]，LDA[4,5]方法都是在高维向量空间上进行特征提取。然而，在现实的空间中，将图像矩阵样本转换为向量的过程中，破坏了图像矩阵样本原有的几何结构，导致一些有用信息的损失。

近年来基于矩阵模式的特征提取算法(如文献[6-8])由于能有效地提高识别率、节省计算时间，被广泛的研究。如文献[6]提出的矩阵模式的Fisher线性判别准则(MatFLDA)、矩阵模式的主成份分析方法(MatPCA)不但在处理图像数据时使用矩阵模式，尽可能地保留原始的数据信息，而且，提出一种将矢量数据转换成矩阵模式的方法，大大扩展了矩阵模式的应用范围。

矩阵模式的Fisher线性判别准则(MatFLDA) 虽然避免了基于向量方法的缺点，具有较好的特征提取能力，然而，MatFLDA方法作为全局判别准则，算法中使用总体均值来替代方差，对于那些具有明显局部流形的数据，比如人脸数据、高维文本数据等等，MatFLDA方法一定程度上缺乏适应性。为了确保样本数据的局部信息，我们在本文的方法构造中引入局部保持投影(Locality Preserving Projections, LPP)[9]流形学习方法中通过嵌入样本的最近邻图，提取样本空间的局部结构信息这一思想。

本文在MatFLDA基础上，引入局部加权均值(Local Weighted Mean,LWM)[10]的概念，提出一种具有局部学习能力的特征提取方法：基于矩阵模式的局部子域最大间距判别分析(Local Sub-domains Maximum Margin Criterion Based Matrix Pattern,Mat-LSMMC)。该方法具有如下优势：(1)Mat-LSMMC方法运用了矩阵模式，提高了特征提取能力，大大降低了空间复杂度，同时消除了一般行(列)向量所带来的限制；(2)Mat-LSMMC方法使用了最大间距准则(Maximum Margin Criterion,MMC)[11,12]，避免小样本问题[13]；(3)Mat-LSMMC方法中用LWM替代标准均值，一定程度上较好地反映不同样本在保持内在局部结构方面的贡献程度大小，实现了局部保持。

在实验中，通过测试传统的UCI数据集和人脸识别数据集，表明本文的Mat-LSMMC方法具有上述优势。

1 相关工作

为了便于描述，我们在本节简单回顾一下LWM、MatFLDA方法的概念。

1.1 局部加权均值:LWM

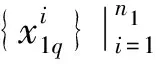
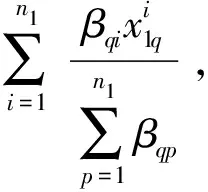
从定义1可以看出，LWM是通过给在局部子域中的样本分配不同权值来表示不同样本在保持内在局部结构所反映的贡献程度的不同。

1.2 矩阵线性判别分析 MatFLDA

定义2 (MatFLDA)：假设有n个样本组成的样本集A={A1,…,An}，Ai(i=1,2,…,n)均是矩阵模式，分别属于C个不同的类，第c类大小为nc，给定分类决策平面的法向量ω。则MatFLDA的类内、类间散度矩阵和目标函数为：

2 基于矩阵模式的局部子域最大间距判别分析：Mat-LSMMC

在矩阵模式的基础上，结合局部加权子域的概念，本文提出了一种新的算法Mat-LSMMC，见图1。我们用文献[6]的方法将每个矢量数据转换为矩阵模式，在样本数据中结合1.1节中局部加权均值LWM的概念，运用流形学习算法中的局部保存思想将数据有效划分为各个局部加权子域，寻找每个局部加权子域的类内最近邻局部子域(Within-class Nearest Neighbor Local Sub-domains,WNNLSD)和类间最近邻局部子域(Between-class Nearest Neighbor Local Sub-domains,BNNLSD)，构造对应的具有明显几何含义的矩阵模式类内散度和类间散度。

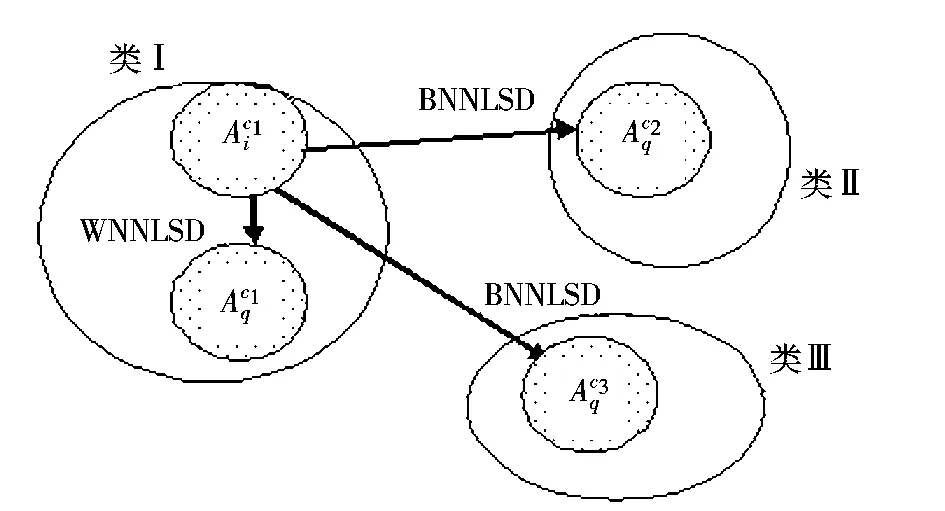
图1 Mat-LSMMC原理图Fig.1 The schematic diagram of Mat-LSMMC

下面定义本文Mat-LSMMC方法的类内散度矩阵和类间散度矩阵。

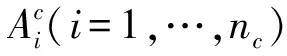
(1)

(2)

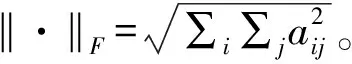
则本文Mat-LSMMC方法的目标函数为：

(3)

为了提高本文Mat-LSMMC方法求解目标函数的效率，我们对式(1)、式(2)进行改写和简化，由此，我们得到如下定理。

定理1 根据定义3，式(1)、式(2)分别可以简化为：

(4)

(5)

其中：

则式(1)可以表示为：

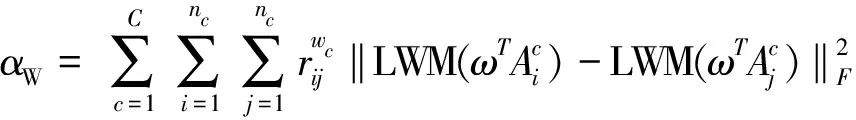
则式(4)成立。

算法：基于矩阵模式的局部子域最大间距判别分析。

Algorithm：Mat-LSMMC

Input:数据集X，并给kc，h赋初值；

Output:变换矢量ω；

Step1:对矢量表示的样本根据文献[6]的方法转换成矩阵模式；

Step2:根据给定的kc，将数据集A划分成若干个局部子域；

Step4:根据定义3，构造相应的类内散度矩阵和类间散度矩阵；

Step5:根据定理1，求解式(3)，得到满足式(3)最大特征值对应的矢量ω。

3 实验

通过测试4个UCI数据子集(即：IRIS、Ionosphere、Wine、Glass)、两个人脸识别数据集(ORL、Yale)来说明Mat-LSMMC方法具有较好的特征提取能力。在实验过程中都使用最近邻分类器。

3.1 测试UCI数据集

通过测试4个UCI数据子集(见表1)来说明Mat-LSMMC方法具有较好的特征提取能力，并将Mat-LSMMC方法同MatPCA、MatFLDA、MatMMC 3种特征提取方法进行比较。测试过程中Mat-LSMMC的参数：K∈[2,5]，h∈2t，t∈(-500,500),γ∈(0,1)，使用10-折交叉验证。测试结果见表2。

表1 Ionosphere、IRIS、Wine、Glass数据集
Table1IonosphereIRIS,Wine,Glass,datasets

DatasetsThe Number of Training SamplesThe Number of Test SamplesThe Number ofFeaturesThe Number of SubjectsMatrix ModelIonosphere23011733211×3IRIS10050432×2Wine1186012310×6Glass14272963×3

从表2，我们可以得到以下结论：

(1)Mat-LSMMC同其他3种方法相比,其精度较大。说明Mat-LSMMC方法具有较好的特征提取。Mat-LSMMC方法中运用了局部流形学习方法中构造近邻拉普拉斯图的方法，实现了局部保持，提高了特征提取效果和分类精度。

(2)Mat-LSMMC由于是基于矩阵模式下的特征提取方法，空间复杂度较低。

(3)Mat-LSMMC方法由于使用了最大间距准则，避免了matFLDA方法的小样本问题。

3.2 测试人脸数据

人脸图像数据集蕴含着内在的非线性流形结构。通过测试ORL(32×32)(40个类，每类10个样本)和Yale(32×32)(15个类，每类11个样本)两个人脸图像数据集来表明Mat-LSMMC方法在一定程度上能解决小样本问题，具有较好的特征提取能力。

在测试过程中,为了有效说明Mat-LSMMC方法的优势，我们使用PCA、MatPCA、MatFLDA、MatMMC 4种方法来对比测试，Mat-LSMMC参数的设定同3.1。测试结果见表3。

表2对Ionosphere 、IRIS、Wine、Glass数据集的识别效果比较
Table2ReoognitionperformancecomprisononIonosphereIRIS,Wine,Glassdatasets

DatasetsAlgorithmMatPCAMatFLDAMatMMCMat-LSMMCIonosphereAccuracy0.906 00.863 20.897 40.9316(K=3;h=25;γ=0.3)IRISAccuracy0.940.940.961(K=5;h=2-3;γ=0.5)WineAccuracy0.716 70.733 30.766 70.8(K=5;h=2-10;γ=0.25)GlassAccuracy0.833 330.805 60.847 20.875(K=3;h=2-5;γ=0.1)

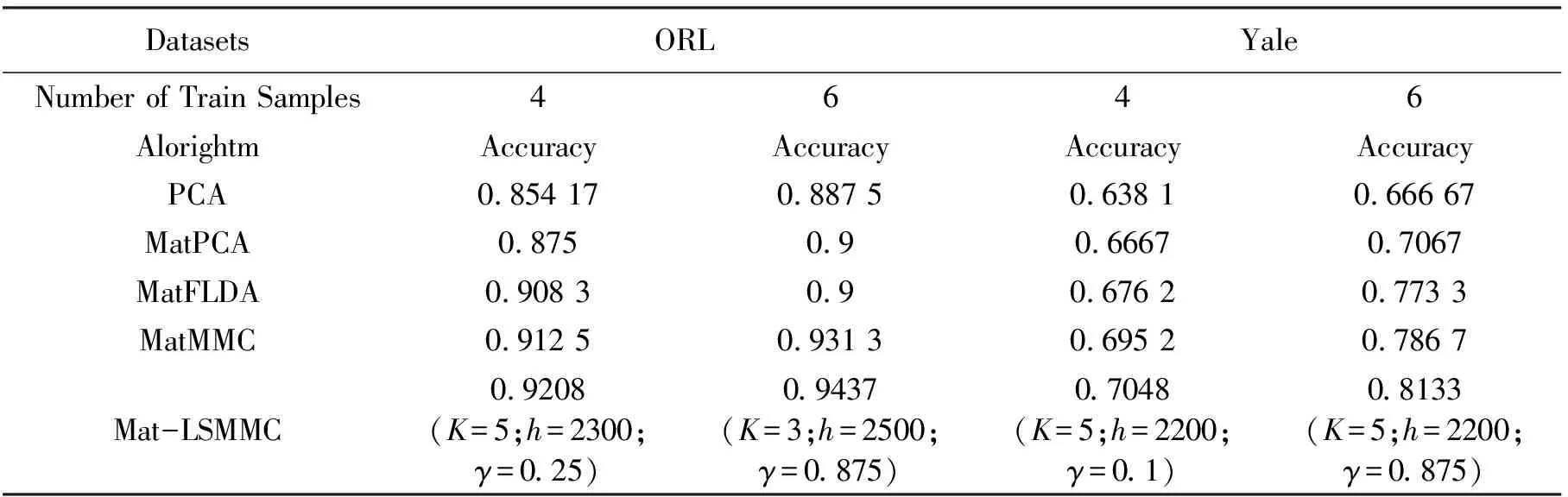
表3对ORL、Yale数据集识别效果比较
Table3ThecomparisonofORL,Yaledatasetrecognitioneffect

DatasetsORLYaleNumber of Train Samples4646AlorightmAccuracyAccuracyAccuracyAccuracyPCA0.854 170.887 50.638 10.666 67MatPCA0.8750.90.66670.7067MatFLDA0.908 30.90.676 20.773 3MatMMC0.912 50.931 30.695 20.786 7Mat-LSMMC0.9208(K=5;h=2300;γ=0.25)0.9437(K=3;h=2500;γ=0.875)0.7048(K=5;h=2200;γ=0.1)0.8133(K=5;h=2200;γ=0.875)

为了提高测试结果的有效性，在测试过程中分别对ORL、Yale数据集选取4个、6个样本作为训练样本来测试上述4种方法，并分别使用4-折交叉验证和6-折交叉验证。

根据上述结果，我们可以得到如下结论：

(1)Mat-LSMMC方法在处理人脸数据时，比其他方法具有更好的特征提取效果和分类精度,说明此方法由于引入了LWM来替代标准均值，较好地反映了不同样本在保持样本内在局部结构方面的贡献程度的差异，更好地保持样本内在蕴含的几何结构。

(2)Mat-LSMMC方法处理32×32图像数据集时，直接使用矩阵模式，如果用矢量形式表示，则需要存储1 024×1 024的散度矩阵，而本文的方法则只需要存储32×32散度矩阵，所占空间只是原方法的1/1 024，大大降低了空间复杂度。

(3)Mat-LSMMC方法使用了最大间距判别分析，不存在小样本问题。

4 总结

本文在矩阵模式的基础上，提出了具有一定局部学习能力的Mat-LSMMC方法。该方法结合局部加权均值概念，使用流形学习理论对原样本空间进行有效划分，一定程度上提高了算法的局部学习能力。同时，由于采用矩阵模式使得算法空间复杂度大大的降低。最后通过测试人造、真实数据集来表明本文Mat-LSMMC方法具有较强的特征提取能力。当然，Mat-LSMMC方法也存在着一定的不足，比如如何更好地确定近邻参数和热核参数，更有效地提高该方法的执行效率，将是我们以后研究的方向。

参考文献：

[1] Bian Z Q, Zhang X G. Pattern Recognition[M].Beijing: TsingHua University Press, 2001.

[2] Jolliffe I T. Principal Component Analysis[M].New York: Springer-Verlag, 1986.

[3] Todorov, Valentin, Filzmoser, et al. Comparing classical and robust sparse PCA[C].Advances in Intelligent Systems and Computing. Berlin:Springer Verlag, 2013:1 283-1 291.

[4] Li Ronghua, Liang Shuang, Baciu George, et al. Equivalence between LDA/QR and direct LDA[J].International Journal of Cognitive Informatics and Natural Intelligence,2011,5(1):94-112.

[5] Dhir Chandra Shekhar, Lee Sooyoung. Discriminant independent component analysis[J].IEEE Transactions on Neural Networks,2011,22(6):845-857.

[6] Chen S C, Zhu Y L, Zhang D Q, et al. Feature extraction approaches based on m atrix pattern: matPCA and matFLDA[J].Pattern Recognition Letters, 2005,26(8):1 157-1 167.

[7] He Xiaofei, Cai Deng, Niyogi Partha.Tensor Subspace Analysis[C].Advances in Neural Information Processing Systems. 2005 Annual Conference on Neural Information Processing Systems. Canada: Neural information processing system foundation, 2005:499-506.

[8] Jun Gao, Chung Fulai, Wang Shitong. Matrix pattern based minimum within-class scatter support vector machines.Applied Soft Computing Journal,2011,11(8):5 602-5 610.

[9] Wong W K, Zhao H T. Supervised optimal locality preserving projection[J].Pattern Recognition, 2012,45(1):186-197.

[10] Atkeson, Christopher G, Moore, et al. Locally weighted learning[J].Artificial Intelligence Review, 1997,11(1-5):75-113.

[11] Yang Wankou, Sun Changyin, Du Helen S, et al. Feature extraction using Laplacian Maximum Margin Criterion[J].Neural Processing Letters, 2011,33(1):99-110.

[12] Cui Yan, Fan Liya. Feature extraction using fuzzy maximum margin criterion[J].Neurocomputing, 2012,86(1):52-58.

[13] Deng Weihong, Liu Yebin, Hu Jiani, et al. The small sample size problem of ICA: A comparative study and analysis[J].Pattern Recognition, 2012,45(12):4 438-4 450.