基于信息耦合度的群集式AUV分群控制算法

刘明雍, 杨盼盼, 雷小康, 刘坤

(西北工业大学 航海学院, 陕西 西安 710072)

自主水下航行器(autonomous underwater vehicle,AUV)群集的协同控制是目前AUV的热点研究领域之一[1-2]。通常,群集式AUV的协同行为分为2种:组群和分群。组群要求某一区域内随机分布的AUV能聚集并以编队的方式共同执行任务。与组群相反,分群表征为AUV群集在外部刺激下分裂为多个子群的行为,可用于分群避险、分群监控、分群搜索等场合。通常,AUV群集由大量成本低廉、配置简单、能力有限的微小型AUV组成,个体完全相同,不存在显式的差异,且地位均等无主从之分。这种AUV的群集运动,实质上是一种无中心控制的涌现行为,其显著特点是个体行为仅受周围邻居的影响,相互之间不存在任何形式的协商、指派等高级智能化的协调机制。类似系统的分群行为在生物界中亦广泛存在,如分群觅食的鸟群[3]、分群避险的鱼群[4]等。研究表明:这些生物群体在诸如食物、危险等外部信息的触发下,个体间的关联强度可决定分群行为是否发生以及发生的规模[5-6]。

目前对分群控制的研究,尚处于十分欠缺的阶段。文献[7]借助于个体间的身份标识,通过不同的人工势场函数实现了异构机器人的分离;文献[8-9]基于指派机制,通过为个体指定跟踪目标实现了群集的分裂;文献[10]在全局通信的支持下,利用同伦参数切换控制律,完成了群集的分裂与融合运动。近来,刘明雍[11-12]等研究了一类无中心控制下,不依赖于任何协商和指派机制的分群控制问题,提出了一种基于邻域跟随的分群控制算法。

本文针对无协商、指派及中心控制的AUV自发分群问题,提出了一种基于信息耦合度(information coupling degree:ICD)的分群控制算法。首先根据生物分群行为设计了融合AUV与其邻居相对位置、速度和邻居数量的信息耦合度函数。然后,利用个体间信息耦合度设计了一种分布式分群控制算法,在外部刺激下使AUV运动行为产生分化,从而使AUV群集涌现出分群运动的现象。最后通过仿真实验验证了所提控制方法的分群可行性和有效性。

1 数学模型及相关描述

对于在水下运行的N个AUV组成的群集系统,由于个体间地位平等无显示差异,其个体动力学模型可统一由以下二阶方程描述:

(1)

式中,pi、vi∈R3分别为AUVi的位置和速度向量,ui∈R3为其加速度向量,在此作为控制输入。

根据AUV群集系统的特点,在此引入本文需要

用到的相关概念,并作简要说明。

定义1 邻域:以AUVi自身位置pi为圆心,感知范围R为半径的圆周。定义2 邻居:AUVi邻域范围内所有的个体称为其邻居。用集合表示为Ni={j:‖pj-pi‖≤R,j≠i,j=1,2,…,N}。其中,‖pj-pi‖为AUVj与AUVi间的欧氏距离。定义3 信息耦合度:表征AUV个体与其邻居间的相互关联关系,体现了AUV间耦合程度的强弱。对于由N个AUV构成的群集系统,其信息耦合度C可用矩阵表示为:

(2)

式中：cij=f(pij,vij,|Ni|,…)为信息耦合度函数,与个体间距离、邻居运动参数、邻居数量等多个因素有关。当AUVi与AUVj超出其邻域范围时,cij=0,即两AUV间无耦合关系;并在此规定AUV与其自身的信息耦合度为0,即cii=0。

本文的研究目的在于:通过建立适当的信息耦合度表征AUV间的耦合交互关系,并在此基础上设计无中心控制的分群控制算法,实现AUV群集的自发分群运动。

2 基于信息耦合度的AUV分群控制方法

2.1 信息耦合度设计

参考生物分群过程中个体间的作用机理[5-6],综合考虑AUV的位置、速度和周围邻居数量信息,将信息耦合度函数设计为:

cij=(ξij+ωij)×ηij

(3)

从(3)式中可看出,信息耦合度由3部分组成:

1)ξij为位置耦合项,与AUV间的相对位置有关,可写为:

(4)

式中：rij>0为位置耦合强度系数,σ>0,α<1/2为固定参数。

2)ωij为速度耦合项,由AUV间的相对速度决定。ωij更新律如下:

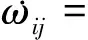
(5)

式中：μij>0为AUV间的速度耦合强度系数,Γ=diag{γ1,γ2,…,γn}为n维正定对角矩阵。

3)ηij为信息耦合度中与周围邻居数量有关的耦合项:

(6)

式中：|Ni|为AUVi的周围邻居数,κij>0为强度调节系数,β为可调幂级数。

从(3)式～(6)式可以看出,所设计的信息耦合度函数能够反映自然界生物群集中个体感知强度随距离衰减、对邻居运动速度变化敏感及受邻居数量影响等现象,可用于对个体间耦合强度进行表征。

2.2 AUV分群控制算法

基于信息耦合度的分群控制原理如图1所示,为简化起见,取AUV群集中的4个AUV进行说明。

图1 基于信息耦合度的分群控制基本原理

图1中,假设AUV 1和4分别为群集中感知外部刺激信息并做出应激反应的个体(其运动速度分别为v1和v4,方向如图1所示),AUV2和3未能感知外部刺激,运动行为仅由其邻居决定。当AUV间的信息耦合度c12>c23,c34>c23时,AUV 2和3分别受到AUV 1和4更强的耦合作用,运动行为有与其趋于一致的趋势。在此作用下,AUV 2和3之间的信息耦合度逐渐减小并最终断开耦合作用,从而使群集出现分裂现象。

综合上述分群原理,基于信息耦合度的分群控制律可以写成:

(7)

式中:

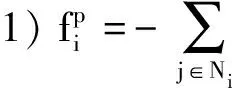
(8)

A为势场作用强度系数,L为AUV群集结构系数。

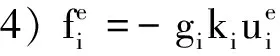
基于上述分群控制规则,AUV可在信息耦合度的作用下根据周围邻居的位置、速度及邻居数量信息建立不同的耦合强度,从而在分群控制项的作用下产生不同的运动倾向性,导致运动行为产生分化,使较强信息耦合度个体聚集而较弱信息耦合度个体分离,最终实现外部刺激作用下的分群运动。

3 仿真实验及结果分析

在Matlab下对本文所提出的基于信息耦合度的AUV分群控制算法进行仿真研究。选取在定深空间中运行的20个AUV作为仿真实验对象,其初始位置任意分布在[0,20]×[0,20]区域内,初始速度以任意方向分布在区间[0,10]×[0,10]内,仿真步长取0.01 s。其他仿真参数选为:R=5 m,rij=10,σ=1,α=0.4,μij=0.05,Γ=diag{1,1,…,1},κij=0.5,β=2,A=10,L=3。

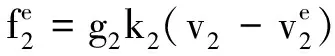
(9)

在外部刺激作用下,AUV 1和AUV 2运动行为产生分化,逐渐与外部刺激信号的参考速度趋于一致。此时,在分群控制律(7)的作用下,AUV间由于信息耦合度的不同,开始进行分群运动,仿真结果如图2至图4所示。

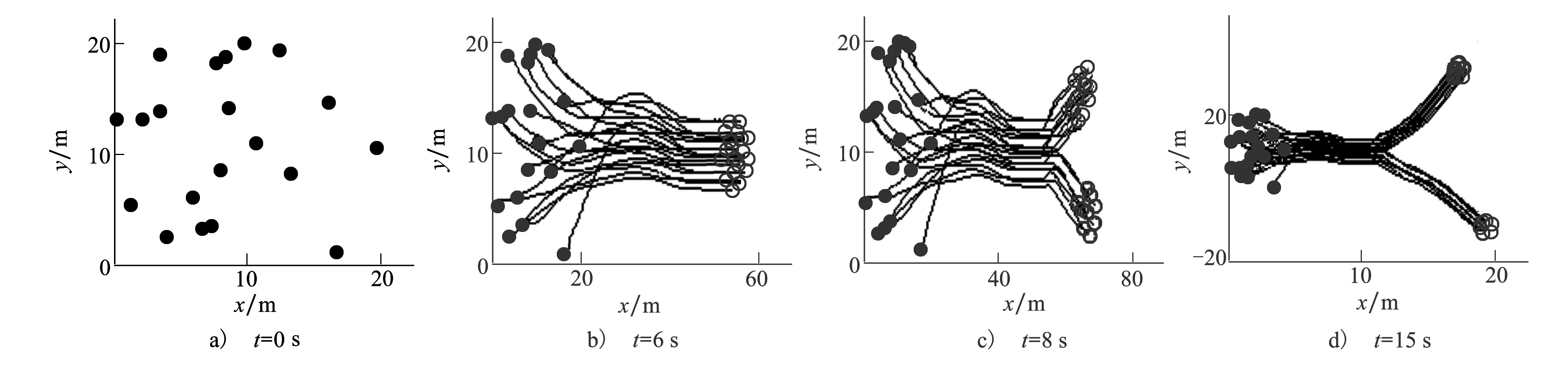
图2 AUV分群过程中的运动轨迹

图2为AUV分群运动的动态演化过程,其中“·”表示AUV的初始位置,“∘”表示AUV在t时刻的位置,曲线为其运动轨迹。a)中为AUV在t=0s时刻的位置分布;b)为t=6 s时刻AUV群集通过组群运动形成稳定编队;c)为t=8 s时刻AUV群集在外部刺激信号的作用下运动行为出现分化,逐渐分裂成2个子群;d)为t=15 s时刻AUV群集的最终运动状态,此时2个子群脱离相互耦合关系,独立编队运行。

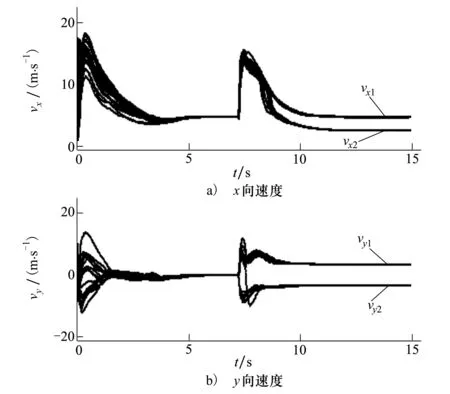
图3 AUV分群过程中速度变化曲线

图3为分群过程中AUV在x和y方向上速度分量的变化曲线。从中可以看出,在t<7 s无外部刺激信号时,群集通过组群行为实现编队运动,各AUV的运动速度达到一致值[5 0]Tm/s;当t=7 s分群行为开始发生后,分裂出的2个子群运动速度产生分化,最终子群在x和y方向上速度与群集边缘受外部刺激个体的速度趋于一致。其中,子群1中AUV的速度趋近于[5 5]Tm/s,子群2中AUV的速度趋近于[3 -5]Tm/s。

由于AUV无任何差异,不失一般性,选取分群过程中AUV 10与其余AUV间信息耦合度的变化曲线进行分析。如图4所示,实线表示AUV 10与同子群中AUV间的信息耦合度,虚线表示AUV 10与不同子群中AUV间的信息耦合度。从中可以看出,在AUV群集做编队运行时,AUV 10与其周围邻居间的信息耦合度趋于常值并保持稳定;当分群运动开始时,由于AUV 10周围邻居运动状态发生变化,导致其与其周围AUV间的信息耦合度产生变化。从图4中可以看出,分群开始后AUV 10与同子群中AUV间信息耦合度在外部刺激下产生波动,但最终稳定为一个常值;而AUV 10与不同子群中AUV间的信息耦合度逐渐减小,当超出邻域范围后相互间的信息耦合度迅速降为0,不再有耦合交互作用。

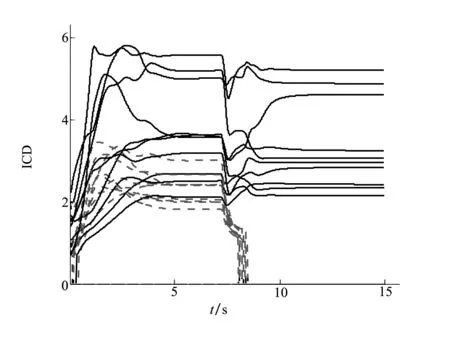
图4 分群过程中AUV 10与邻居间信息耦合度变化曲线

从上述仿真结果可以看出,本文所设计的分群控制算法能实现无中心控制下AUV群集的分群运动,子群中个体的速度最终趋于一致,且信息耦合度能较好的反映分群过程中AUV个体间耦合强度的变化情况。

4 结 论

本文研究了在无中心控制下,基于信息耦合度的群集式AUV分群控制算法。在自然界中生物群集分群行为的启发下,设计了融合邻居位置、速度及邻居数量的信息耦合度函数,并根据信息耦合度不同导致的AUV交互强度差异可使个体分离的原理,提出了一种分布式分群控制算法。仿真实验表明,该算法控制下的AUV群集在受到外部刺激作用时,无需指派、协商等智能化方式,仅通过个体间的局部信息交互就能够自发实施分群运动。

参考文献：

[1] Stilwell D J, Bishop B E. Platoons of Underwater Vehicles[J]. IEEE Control System Magazine, 2000, 20(6): 45-52

[2] 许真珍, 封锡盛. 多UUV协作系统的研究现状与发展[J]. 机器人, 2007, 29(2): 186-192

Xu Zhenzhen, Feng Xisheng. Current Status and Future Directions of Multiple UUV Cooperation System[J]. Robot, 2007, 29(2): 186-192 (in Chinese)

[3] Bajec I L, Heppner F H. Organized Flight in Birds[J]. Animal Behavior, 2009, 78: 777-789

[4] Partridge B L. Structure and Function of Fish Schools[J]. Scientific American, 1982, 246(6): 114-123

[5] Couzin I D, Laidre M E. Fission-Fusion Populations[J]. Current Biology, 2009, 19(15): 633-635

[6] Li Jinchao, Sayed A H. Modeling Bee Swarming Behavior through Diffusion Adaption with Asymmetric Information Sharing[J]. EURASIP Journal on Advances in Signal Processing, 2012, 18: 1-17

[7] Kumar M, Grag D P, Kumar V. Segregation of Heterogeneous Units in a Swarm of Robotic Agents[J]. IEEE Trans on Automatic Control, 2010, 55(3): 743-748

[8] 刘宗春, 田彦涛, 李成凤. 动态阻尼环境下多领导者群体机器人系统协同跟踪控制[J]. 机器人, 2011, 33(4): 385-393

Liu Zongchun, Tian Yantao, Li Chengfeng. Coadaptive Following Control of Swarm Robot System with Multiple Leaders in Dynamic Damping Environment[J]. Robot, 2011, 33(4): 385-393 (in Chinese)

[9] Su Housheng, Wang Xiaofan, Yang Wen. Flocking in Multi-Agent Systems with Multiple Virtual Leaders[J]. Asian Journal of Control, 2008, 10(2): 238-245

[10] Mrogan D S, Schwartz I B. Dynamic Coordinated Control laws in Multiple Agent Models[J]. Physics Letters A, 2005, 340: 121-131

[11] 刘明雍, 雷小康, 彭星光. 融合邻域自适应跟随的群集系统分群控制方法研究[J]. 西北工业大学学报, 2013, 31(2): 250-254

Liu Mingyong, Lei Xiaokang, Peng Xingguang. A Control Algorithm for Flock Fission Based on Adaptive Local Following Interaction[J]. Journal of Northwestern Polytechnical University, 2013, 31(2): 250-254 (in Chinese)

[12] 雷小康, 刘明雍, 杨盼盼. 基于邻域跟随的群集系统分群控制算法[J]. 控制与决策, 2013, 28(5): 741-745

Lei Xiaokang, Liu Mingyong, Yang Panpan. Fission Control Algorithm for Swarm Based on Local Following Interaction[J]. Control and Decision, 2013, 28(5): 741-745 (in Chinese)