基于加权集对分析的嵌入式计算机性能评价模型

游永彬, 刘丽艳, 荆瑞俊

(西北工业大学 自动化学院, 陕西 西安 710072)

嵌入式计算机性能提升速度迅猛,但是嵌入式应用的规模量级也在不断提升,为了满足日益复杂、庞大的应用需求,仅有高速的运行环境是不够的。嵌入式计算机系统的性能评价和分析是目前正在研究的热点课题,它与嵌入式计算机体系结构、嵌入式计算机软件和算法共同构成了嵌入式计算科学的四大支柱,并且在算法与系统的设计与实现过程中发挥着重要的作用。事实上,不同类型应用程序的运行效果只能反映不同的性能指标,而只有综合所有这些不同的性能指标,才有可能对系统的整体性能做出恰当评价。科学地进行嵌入式计算机的性能分析有助于更好地发挥嵌入式计算机的系统性能,提高软硬件的开发质量。

目前,评价嵌入式计算机综合性能的方法有很多种[1-3],例如层次分析法、模糊数学法、灰色综合评价方法等,每种方法都有各自的优点与不足,许多学者针对各评价方法的不足做了相应修正,取得了一些成果。事实上,由于嵌入式计算机是一个复杂体系,影响其性能的诸多因素具有不确定性和模糊性,这些因素与嵌入式计算机性能好坏间存在着复杂的非线性关系,至今没有统一的嵌入式计算机性能评价模型。另外,影响嵌入式计算机的众多因素值主要是通过基准测试程序获取,在这个过程中不可避免产生随机误差,也对最终评价结果产生一定影响。

集对分析理论[4]是我国学者赵克勤于1989年提出的一门新的处理不确定性问题的系统理论方法,其核心思想是把确定、不确定视作一个确定不确定系统,在这个系统中将确定性分为“同一”与“对立”2个方面,将不确定性称为“差异”,从同、异、反三方面分析事物及其系统。同、异、反三者相互联系、相互影响、相互制约,又在一定条件下相互转化[5]。通过引入联系度及其数学表达统一描述各种不确定性,从而将不确定性的辩证认知转化为数学运算。

本文尝试运用集对分析理论,借助确定性和不确定性对样本进行定性分析,再通过计算联系度对嵌入式计算机做出定量评价,最后结合序关系分析法对嵌入式计算机性能做出全面、客观的评价。

1 基于加权联系度的性能评价模型

1.1 嵌入式计算机性能评价指标体系的建立

为了统一考察评估对象,必须建立一个评估准则。嵌入式计算机评估指标体系就是一个评估准则,它使用同一评估尺度对不同嵌入式计算机进行比较。本文从微处理器性能、传输性能、存储性能、可靠性和实时性这5个方面分析嵌入式计算机性能,为了更清楚地描述性能,将上述的几大指标逐步细化,形成一个3层次的嵌入式计算机性能评价指标体系,具体指标体系见表1所示。

表1 嵌入式计算机性能评价指标体系

1.2 集对分析理论概述

定义1在问题背景W下把2个具有一定联系的集合A、B组成集对，记为H=(A,B)，按照集对的某一特性展开分析，找出2个集合共有的特性、对立的特性和既非共有又非对立的特性称之为差异特性，并建立在该问题W下集对H的同异反联系数μ(H,W)，其表达式见公式(1)。

μ(H,W)=S/N+(F/N)I+(P/N)J

(1)

式中:N是集对H的特性总数，S是两集合共有的特性个数，P是2个集合相互对立的特性个数，F=N-S-P是两集合的差异特性个数；分别称S/N、F/N、P/N为集对H在问题W下同一度、差异度、对立度；J是对立型关系数的标记，需要根据不同的对立类型取值，I是差异度的标记，它的取值与J有关。当同异反关系是正负型对立关系时，取J=-1，这时I∈[-1,1]；当同异反关系是倒数型对立关系时，取J=1/R，其中R是同一度中的最小数，此时，I∈[1/R,1]。

令a=S/N,b=F/N,c=P/N，则上式可表示为：μ(H,W)=a+bI+cJ，此时有a+b+c=1。

定义2[6] 在联系数μ(H,W)=a+bI+cJ，记

shi(μ)=a/c

(2)

称sin(μ)是联系数μ的态势。

1.3 嵌入式计算机性能评价模型

将集对分析法用于嵌入式计算机性能评价模型,其实质就是将嵌入式计算机性能评价指标值与最优方案进行形成对子组成一个集对,通过计算各嵌入式计算机性能评价指标与最优方案之间的联系度确定方案的优劣。

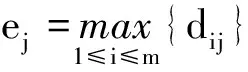
再应用公式(2)给出了第i个嵌入式计算机的加权联系度μi的计算方法。

(3)

式中：wj(j=1,2,…,16)是采用序关系分析法确定的嵌入式计算机性能评价指标uj的权重系数

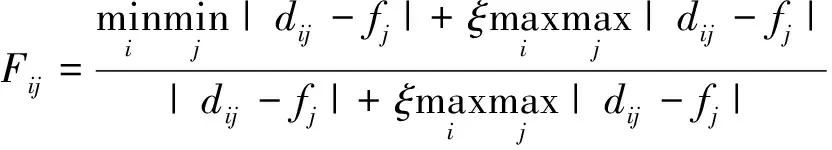
式中：ξ∈(0,1)是分辨系数。

最后,应用公式(2)计算加权联系度μi的态势shi(μi),显然态势shi(μi)越大,表明该嵌入式计算机性能越优,反之则越差。

2 实例分析

为了验证本文算法的有效性,以3种嵌入式计算机为例,具体介绍该方法的应用。A型嵌入式计算机是一种新兴嵌入式计算机,计算先进,性能稳定;B型嵌入式计算机是A型嵌入式计算机的改进型,增加了存储能力;C型嵌入式计算机是一种旧型嵌入式计算机,各个性能都比较差。应用本文提出的算法,对这3种型号的嵌入式计算机进行综合性能评价和优劣比较,具体步骤如下:

步骤1 建立嵌入式计算机性能评价指标体系

根据嵌入式计算机性能参数指标和能够适应未来环境发展的需求,构建了3层的评价指标体系,如表1所示。

步骤2 采用序关系分析法确定指标权重系数

应用序关系分析法确定嵌入式计算机性能评价指标的权重系数,计算结果如下

步骤3 标准化数据矩阵的获取

根据嵌入式计算机性能评价指标体系,应用相应的基准测试程序,获得A、B、C 3款嵌入式计算机性能评价指标值,并对数据进行无量纲化处理,得到标准的数据矩阵D。

步骤4 嵌入式计算机性能优劣排序

根据规范化的数据矩阵D,获得最优方案序列、最差方案序列和中间方案序列分别为:

再应用公式(3)分别计算A、B、C嵌入式计算机相对于最优方案的加权联系度μi(i=1,2,3),

μ1=0.359 1+0.394 5I+0.246 4J,

μ2=0.474 6+0.251 7I+0.276 3J,

μ3=0.265 6+0.220 3I+0.514 1J

最后,应用公式(2)分别计算加权联系度μi

(i=1,2,3)的态势shi(μi),即有:

shi(μ1)=1.457,

shi(μ2)=1.734,

shi(μ3)=0.517

因此,B型嵌入式计算机性能>A型嵌入式计算机性能>C型嵌入式计算机性能,评价结果与实际使用中的性能表现相符。

3 结 论

本文对嵌入式计算机性能的相关因素进行分析,建立了嵌入式计算机性能评价指标体系,结合集对分析理论和序关系分析法,提出了基于加权集对分析的嵌入式计算机性能评价模型。该方法既客观反映了数据本身的作用,又符合具体项目的实际情况。实例应用证明该方法合理有效,为嵌入式计算机的性能评估提供了有价值的参考。

参考文献：

[1] 周延年,朱怡安. 基于组合权重的嵌入式计算机综合性能灰色关联评价算法[J]. 西北工业大学学报, 2011, 29(1): 12-16

Zhou Yannian, Zhu Yi′an. A New and Better Algorithm for Evaluation of Overall Performance of Embedded Computer through Combining Grey Correlation with Assignment Weight[J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 12-16 (in Chinese)

[2] 邢涛,叶景楼,任永昌. 嵌入式系统性能与安全评价方法研究[J]. 科学技术与工程, 2006, 6(1): 76-79

Xing Tao, Ye Jinglou, Ren Yongchang. Study on Effectiveness and Safety Evaluation Methods of Embedded System[J]. Science Technology and Engineering, 2006, 6(1): 76-79 (in Chinese)

[3] 朱怡安,周延年,夏平. 基于熵权的嵌入式计算机性能灰评估[J]. 西北工业大学学报, 2012, 30(5): 647-651

Zhu Yi′an, Zhou Yannian, Xian Ping. A New and Better Algorithm for Evaluation of Overall Performance of Embedded Computer through Combining Grey Evaluation with Entropy Weight[J]. Journal of Northwestern Polytechnical University, 2012, 30(5): 647-651 (in Chinese)

[4] 赵克勤. 集对分析及其初步应用 [M]. 杭州: 浙江科学技术出版社, 2000

Zhao Keqin. Set Pair Analysis and Its Prelimiary Application[M]. Hangzhou, Zhejiang Science and Technology Publishing House, 2000 (in Chinese)

[5] 赵克勤, 宣爱理. 集对论——一种新的不确定性理论方法与应用[J]. 系统工程, 1996, 14(1): 18-23

Zhao Keqin, Xuan Aili. Set Pair Theory——A New Theory Method of Non-Define and Its Applications[J]. Journal of Systems Engineering,1996, 14(1): 18-23 (in Chinese)

[6] 马少斌. 基于区间联系数理论的网络安全风险评估方法及应用 [J]. 自动化与仪器仪表, 2011(4): 115-119

Ma Shaobin. A Network Security Risk Assessment Based on The Interval Connection Number of Quantitative Methods[J]. Automation and Instrumentation, 2011(4): 115-119 (in Chinese)