前后向平均匹配场处理

王奇, 王英民, 苟艳妮

(西北工业大学 航海学院, 陕西 西安 710072)

匹配场被动定位很好地把阵列信号处理的方法和包括信号及噪声在内的全部海洋声学信息融合在一起,因此比传统的平面波波束形成定位算法具有更好的定位精度和更远的定位距离。但匹配场处理(MFP:matched field processing)也有其固有的缺点:此方法过于依赖信道模型,当信道模型与真实环境存在偏差时,匹配场处理的性能急剧下降,且算法的运算量太大,不利于实时处理[1]。

为了提高匹配场处理的稳健性,国内外学者在常规线性匹配场处理器(CMFP:conventional MFP)和自适应匹配场处理器(AMFP:adaptive MFP)的基础上提出了多种稳健算法:如白噪声约束的匹配场处理器(WNCM: white noise constraint method)、邻域位置约束匹配场处理器(MV-NLC: neighborhood location constraints)和环境扰动约束的匹配场处理器(MV-EPC: environmental perturbation constraints)等[2]。以上算法都是通过给匹配场处理器的权向量设计一定的约束条件,从而实现在某些情况下的稳健性,具有一定的局限性。另外，它们的定位性能受到采样协方差矩阵的影响,而采样协方差矩阵包含完整的声场及环境信息,包括对环境失配比较敏感的成分,如果在估计协方差矩阵时能够消除对环境敏感的部分,匹配场处理将获得更稳健的性能。

为了提高匹配场处理的稳健性,本文从采样协方差矩阵估计的角度出发,把阵列信号处理中的前后向平均估计算法引入到了匹配场处理中,提出了前后向平均的白噪声约束匹配场处理器,其实质是对权向量进行白噪声增益约束的同时也对垂直线列阵的阵型进行位置约束。最后用2种方法验证了该算法的性能,一种是用仿真的数据构造采样协方差矩阵并验证算法的有效性,另一种是用北厄尔巴岛的海试数据验证该算法的性能。通过与常规的白噪声约束匹配场处理算法比较可看出,无论是仿真数据还是真实的海试数据,前后向平均匹配场处理器的定位结果都具有更优越的性能,且估计采样协方差矩阵的运算量更小。

1 白噪声约束匹配场处理

为了提高自适应匹配场处理的稳健性,Cox等提出了白噪声约束的匹配场处理器(WNCM),其权向量可以由下面最优化问题求得[3]:

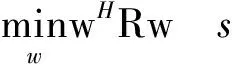
(1)

式中：d为拷贝场向量;σ2为白噪声增益。R是阵列输出协方差矩阵。由拉格朗日乘子法求得,WNCM的权向量为:

(2)

对应的功率输出为:

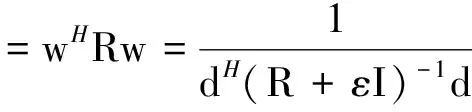
(3)

式中：在采样协方差矩阵的对角线中加了一个较小的量εI,ε是满足(1)式的不平坦噪声约束。在用(3)式进行匹配处理时,需要根据采样的样本估计协方差矩阵R,采样协方差矩阵的估计值会直接影响匹配的效果。

2 前后向平均在匹配场处理中的应用

2.1 数据模型及协方差矩阵的估计

考虑N个阵元均匀分布的垂直线列阵,设阵元间距为l,若入射信号和阵元的夹角为θ,第k个快拍时首阵元接收到的频域信号为s(ω),则第n个阵元的输出可表示为:

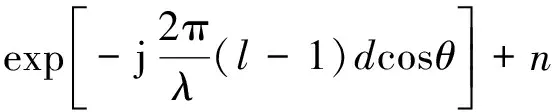
(4)

式中：λ为入射信号的波长;n(ω)为均匀分布的加性高斯白噪声。此时垂线阵的第k个频域快拍是N×1维向量:

xk=[xk1xk2…xkN]T

(5)

由于快拍向量的模型是统计独立同分布的复高斯随机矢量,因此K个快拍的联合概率密度为:

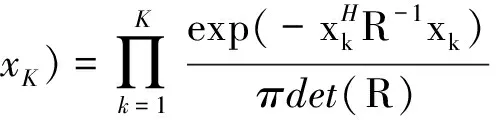
(6)

对联合概率密度取对数并去掉常数项,可得到协方差矩阵的似然函数:

(7)

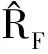
(8)

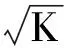
2.2 前后向平均匹配场处理的数学描述

把(5)式所示的频域快拍模型代入(8)式可得:

(9)

由上式可知采样协方差矩阵具有中心共轭对称的特性[4],以此作为约束条件,则(1)式的最优化问题可转化为:

(10)

s.t. wHd=1, wHw≤δ-2, R=JR*J

从上述数学表述可看出,前后向平均匹配场处理是在白噪声增益约束的基础上添加了接收阵阵元均匀分布对协方差矩阵的约束。

在(9)式所示约束条件下求取L(R-1)的最大值,可得到阵型约束下采样协方差矩阵的估计值,称为前后向平均(FB)采样协方差矩阵[4]:

(11)

式中：“T”代表转置;“*”代表共轭。J是一个置换矩阵,其反对角线的元素为1,其余元素为0,如下所示:

(12)

对于方阵J可知,J2=I且JT=J,I为单位阵。把(11)式所示的采样协方差矩阵代入(3)式得到前后向平均匹配场处理器,简写为MFP-FB处理器。

2.3 采样协方差矩阵的快速计算

通常由(8)式直接计算采样协方差矩阵的运算量都比较大,根据阵型的均匀分布的特性可以高效构造前后向平均采样协方差矩阵。

首先当阵元数N为偶数时,把快拍矩阵X分成2个(N/2)×K维矩阵,如下所示:

(13)

当阵元数N为奇数时,把快拍矩阵X分成2个[(N-1)/2]×K维矩阵X1、X2和1个1×K维的行向量xc:

(14)

此时可构造一个实矩阵ZFB。同样,当N为偶数时:

(15)

当N为奇数时:

(16)

然后可如下估计采样协方差矩阵:

(17)

式中：当阵元数N为偶数时:

(18)

当阵元数N为奇数时:

(19)

2.4 运算量分析

1) 前向平均运算量

设阵元数为N,快照数为K,使用(8)式所示前向平均计算采样协防差矩阵需要的复数乘法次数为KN2,所需复数加法次数为(K-1)N2。而一次复数乘法包含4次实数乘法和3次实数加法;一次复数加法包含2次实数加法。因此,前向平均估计协方差矩阵共需要实数乘法次数为:4KN2;共需实数加法次数为:3KN2+2(K-1)N2=5KN2-2N2。因此,实数乘加运算的总量为:9KN2-2N2。

2) 前后向平均运算量

3) 运算量对比

对比两者的运算次数可知,前后向平均算法所需乘法次数比前向平均算法少2KN2;所需加法比后者少3KN2-3N2-2KN次。而乘加运算的总量,前者比后者少:5KN2-3N2-2KN。

易于证明,当K和N为大于1的整数时,5KN2-3N2-2KN恒大于零,即当阵元数和快照数大于1时,前后向平均算法的总运算量小于前向平均算法的运算量。而且通常乘法运算比加法运算需要更多的机器周期,因此从运算需要的时间上看,前者比后者的所需时间更短。

3 仿真分析

3.1 环境参数及接收阵的配置

1993年10月26日和27日SACLANT研究中心在意大利西海岸的北厄尔巴岛附近进行了为期2天的海试。此海区可近似看作均匀海底的浅海海区。该海区的经验环境参数基线模型如图1所示。水层深度为127 m,水层声速在水面到60 m深度处约为1 526 m/s,从60 m到80 m出现跃变,声速较快降到1 510 m/s左右,之后缓慢下降到1 508 m/s;沉积层厚度为2.5 m,沉积层上表面声速为1 520 m/s,下表面声速为1 580 m/s,密度为1.70 g/cm3,衰减为0.13 dB/λ;基底声速为1 600 m/s,密度为1.80 g/cm3,衰减为0.15 dB/λ[5]。由于地声环境参数具有时变性,因此海区环境参数的真实值并非如上图所示的参数值。文中以这些参数值构建拷贝场,并进行匹配场处理。

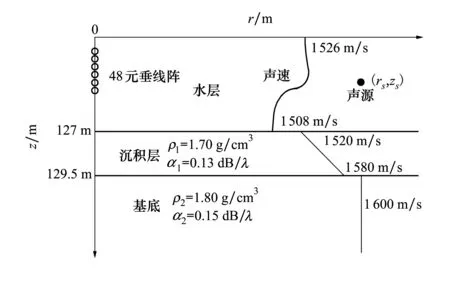
图1 浅海环境模型

实验期间使用一个48元垂直线列阵接收信号,第一个阵元的深度为18.7 m,最后一个阵元的深度是112.7 m,阵元间距为2 m,阵孔径为94 m。阵通过一个砂囊锚定在海底,在2天的实验期间,阵形会随着海浪、洋流等发生变化,无法保持理想情况下的垂直。在构建拷贝场时,假设垂线阵保持绝对的竖直,且阵元等间隔分布。

在2天的实验过程中,均使用HX-90G声源,声源特性保持不变。此声源发射中心频率为170 Hz的伪随机信号,3 dB带宽为12 Hz。数据采集系统的采样频率为1 kHz。在26日的固定声源实验中,声源被锚定在距接收阵5 500±200 m远处,深度约为79 m。在下面的仿真中使用了这次实验采集的数据,分别用MFP-F和MFP-FB型匹配场处理器完成了对固定声源的被动定位。

3.2 主要参数设定及2种定位性能评估参数

使用Kraken简正波模型构建拷贝场[5-6],在算法的仿真运算过程中,设置观测海域的距离从1～10 km,步长100 m;深度从10～120 m,步长0.625 m。

为了对匹配场处理器的性能进行量化评估,引入2个性能评估参数:输出信干比(SINR)和峰值背景比(PBR)。输出信干比定义为:在定位正确的前提下,最大输出功率(通常归一化为0 dB)减去所有网格点输出功率从小到大排序后位于75%的值;若定位失败,输出信干比无意义,设为0 dB(本文为了和其他结果对比方便起见未设为0 dB)。峰值背景比的定义如下:

(20)

式中：P为匹配场处理器的峰值功率,μ为背景平均功率。

3.3 仿真结果及分析

1) 仿真数据处理分析

为了对比理想情况下MFP-F和MFP-FB的定位性能,假设浅海环境精确已知,如图1所示。在此环境下,设声源位于5 900 m远,70 m深处,使用简正波模型仿真产生测量场向量,其中测量场中包含各向同性的均匀高斯白噪声。接着在观测海域的每个网格点处用同样的环境模型产生拷贝场向量,然后分别用2种匹配场处理器进行被动定位。这种情况下若忽略噪声的影响,在声源位置处测量场向量和拷贝场向量可完全匹配。

图2和图3分别是输入信噪比为20 dB时2种处理器的定位结果,图中矩形区域内部的亮点是匹配场处理程序定位的声源。从图中看出2种处理器都能够正确定位。MFP-F的SINR约等于10.25 dB,PBR约等于9.33 dB,计算出的目标位置为(5 900 m,70.0 m);而MFP-FB的SINR约等于14.45 dB,PBR约等于13.34 dB,计算出的目标位置为(5 900 m,68.1 m)。无论从SINR和PBR这2种定位性能评估参数上还是从定位的模糊度图上直观观察都可看出MFP-FB具有更窄的主瓣宽度,且更易于从背景中识别出来。

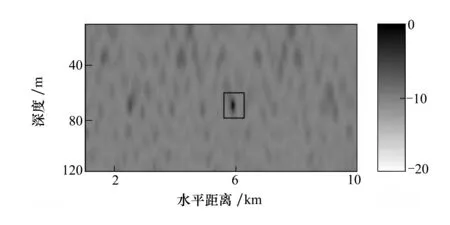
图2 MFP-F定位结果

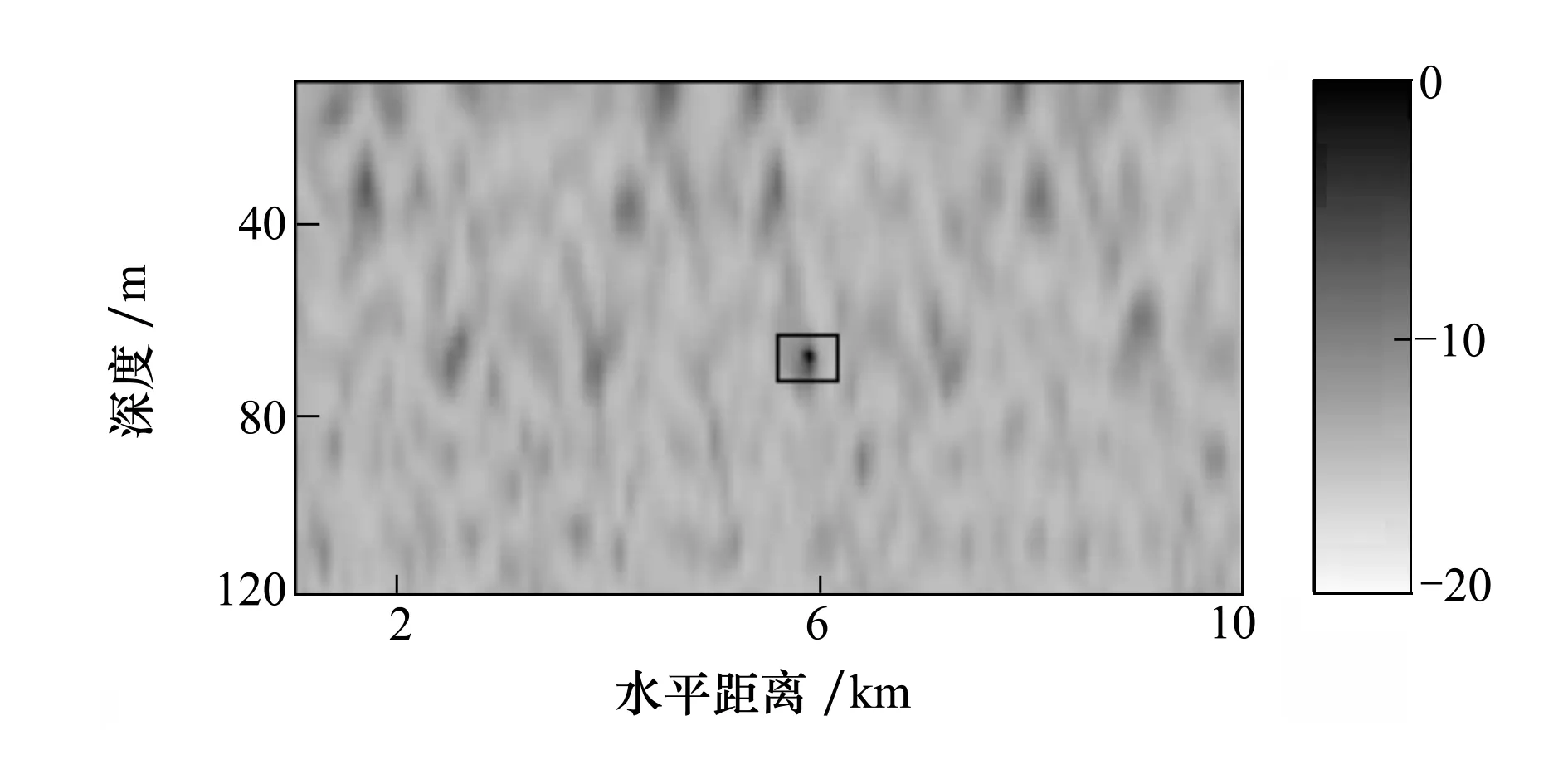
图3 MFP-FB定位结果

图4对比了不同信噪比情况下2种处理器的性能。从图中可看出MFP-FB的SINR比MFP-F至少高约1.5 dB,最多高约5 dB;MFP-FB的PBR比MFP-F至少高约1 dB,最多高约4 dB。从图中也可看出MFP-FB优于MFP-F。

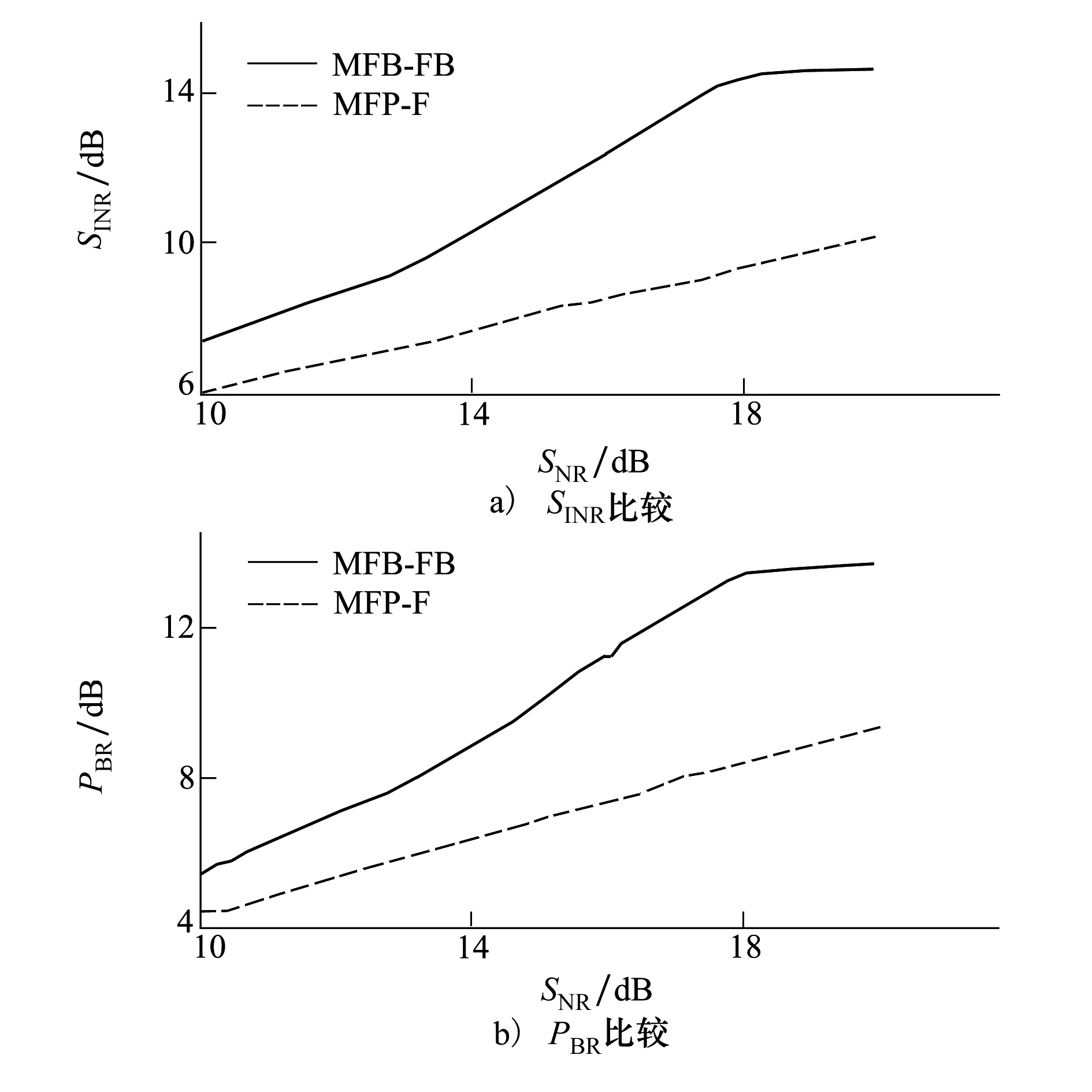
图4 两种处理器性能对比

2) 海试数据处理分析

实际情况下,浅海环境的水声传播信道是一种时变、空变的复杂传播信道,环境参数无法精确获得。下面使用SACLANT研究中心1993年10月26日在北厄尔巴岛附近的海试数据验证本文的匹配场处理算法。26日发射的是连续信号,实验中分别记录了10分钟的数据,本文以每分钟为单元分别对10分钟的数据进行了处理,每分钟都是使用其中前25 s数据组成25个快照,用这些快照估计采样协方差矩阵。其中快照的长度取2 s,快照间的重叠率为50%,对于1 kHz的采样率,每个快照包含2 000个采样点。2种处理器的白噪声约束都设为20 dB。在构建拷贝场时使用图1所示环境参数模型,该环境模型和实测的环境模型具有一定的差异性。

图5和图6分别是2种处理器对第一分钟数据的定位结果。图中矩形内部的亮点是算法计算出的声源位置,而椭圆形表示的是真实目标位置。从图中可看出MFP-F定位失败(88 m,8 200 m),虽然如此在真实声源位置处还是能够看到一个峰值;而MFP-FB可正确定位目标(75 m,5 300 m),且目标比较清楚,其中MFP-FB的SINR约为4.57 dB,PBR约为1.66 dB。

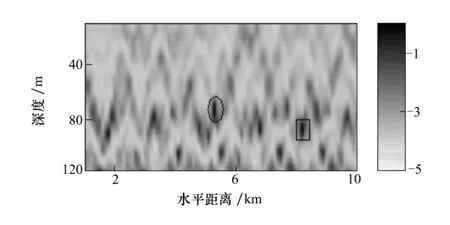
图5 MFP-F真实声源定位

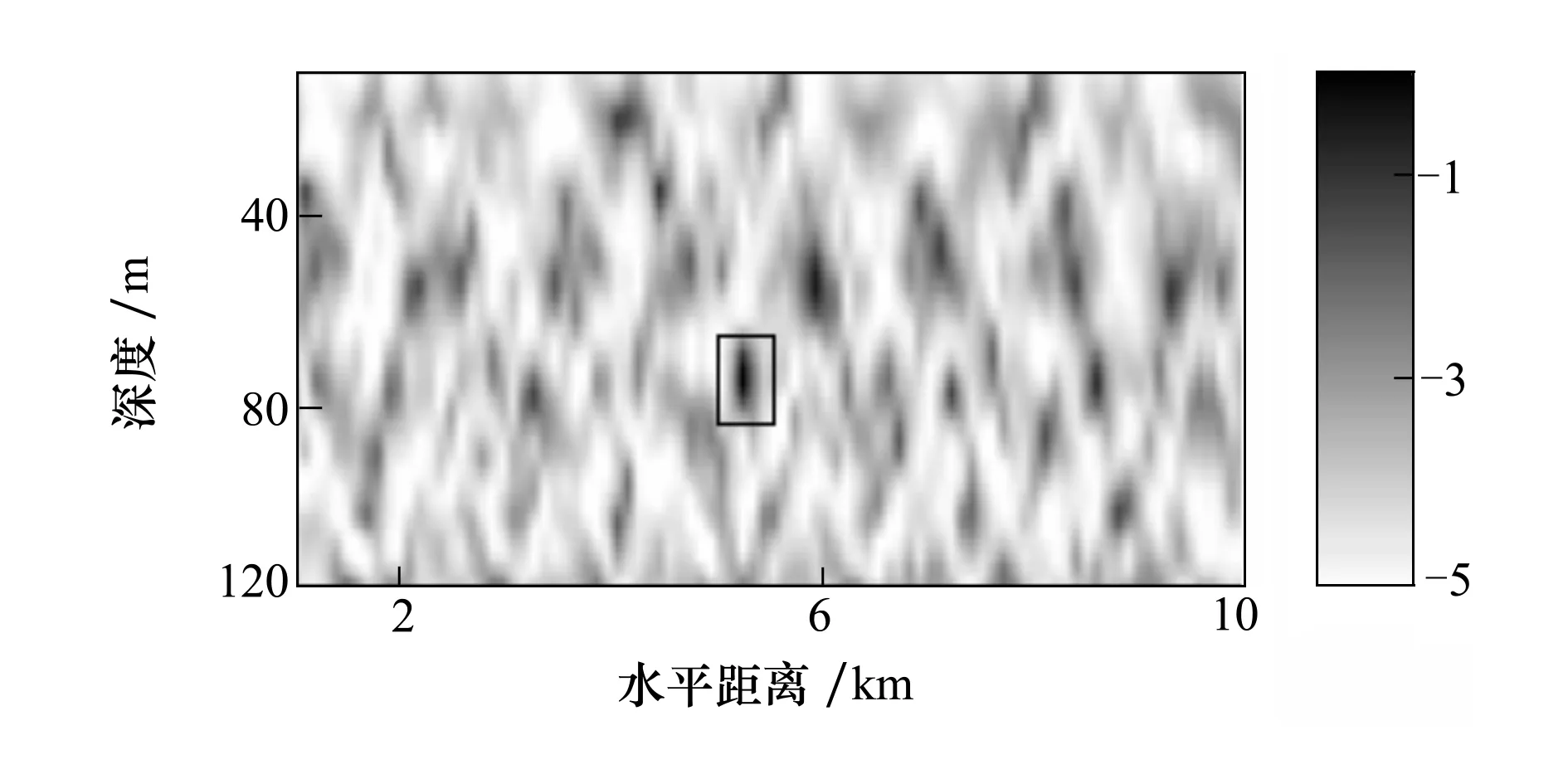
图6 MFP-FB真实声源定位

对其他9分钟采集到的实验数据也进行了相应的处理。MFP-F都无法正确定位目标,但同图5所示接近,在真实声源位置处都存在一个峰值;而MFP-FB在10分钟内都能正确定位,且定位结果都是(75 m,5 300 m)。

Krolik等在文献[5]中使用一种稳健的最大似然算法对相同的实验数据进行了分析处理,得出了和本文相似的定位结果,但是使用Krolik等的算法时不仅需要估计采样协方差矩阵,而且在进行匹配场处理前需要按照对声场的贡献把各阶模态分为可预测模态和不可预测模态,其定位的性能极大的依赖于对模态作用的估计,但对模态作用的估计却缺乏可靠易行的方法,因此他提出匹配场处理算法比本文算法更复杂且不易实现。

对于26日的海试数据,当N=48和K=25时,由2.4节的分析可知,计算采样协方差矩阵时,MFP-F的乘法运算次数为:230 400次;加法运算次数为:283 392次;加乘总运算量为:513 792次。而MFP-FB的乘法运算次数为:115 200次;加法运算次数为:119 904次;加乘总运算量为235 104次。因此,计算采样协防差矩阵时MFP-FB的乘法运算次数比MFP-F少了115 200次,即50%;加法运算次数少了163 488次,即约57.7%;运算总量少了278 688次,即约54%。

4 结 论

由于海洋环境参数会受到季节、地形、温度及洋流等的影响,因而在时间和空间上都具有不确定性因素,且垂线阵在采样的过程中阵元的位置误差以及系统误差等都会导致处理结果的失配,严重制约了匹配场处理的应用。为了提高匹配场处理在复杂环境下的稳健性,本文把前后向平均算法引入到了匹配场处理中。前后向平均匹配场处理的整体思路可归纳为2个部分:①采用白噪声增益约束对权向量进行优化;②从接收阵均匀分布的物理特性出发,用阵元均匀分布的特性对采样协方差矩阵进行约束。从仿真结果和SACLANT研究中心的海试数据处理结果都可看出,该算法的峰值背景比和输出信干比都有所提高,即算法的稳健性和定位性能都得到改善。本文所使用的前后向平均算法可推广到其他的匹配场处理算法中,具有一定的普遍适用性。可以预见,如果把前后向平均算法和其他稳健的匹配场处理器相结合,会得到更好的处理结果。

参考文献：

[1] Baggeroer A B, Kuperman W A, Mikhalevsky P N. An Overview of Matched Field Methods in Ocean Acoustics [J]. IEEE Journal of Oceanic Engineering, 1993, 18(4): 401-424

[2] 杨坤德, 马远良. 基于扇区特征向量约束的稳健自适应匹配场处理器 [J]. 声学学报, 2006, 31(05): 399-409

Yang Kunde, Ma Yuanliang. Robust Adaptive Matched Field Processing with Sector Eigenvector Constraints[J]. Acta Acustica, 2006, 31(05): 399-409 (in Chinese)

[3] Debever C, Kuperman W A. Robust Matched-Field Processing Using a Coherent Broadband White Noise Constraint Processor [J]. The Journal of the Acoustical Society of America, 2007, 122(4): 1979-1986

[4] Trees H L V. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory [M]. New York: Wiley-Interscience, 2002: 1443

[5] Krolik J L. The Performance of Matched-Field Beamformers with Mediterranean Vertical Array Data [J]. IEEE Trans on Signal Processing, 1996, 44(10): 2605-2611

[6] 张歆, 张小蓟, 李斌. 基于Kraken简正波模型的浅海声场分析 [J]. 西北工业大学学报, 2000, 18(03): 405-408

Zhang Xin, Zhang Xiaoji, Li Bin. An Analysis of Shallow Water Channel Using Kraken Normal Model[J]. Journal of Northwestern Polytechnical University, 2000, 18(03): 405-408 (in Chinese)