基于遗传算法SVM的电子元件寿命预测

陈绍炜, 潘新, 刘涛

(西北工业大学 电子信息学院, 陕西 西安 710129)

电子设备应用范围极为广泛，电子元件的可靠性变得越来越重要。其中，电子元件的寿命是衡量可靠性的一个重要标准。

目前的寿命预测中，常用的方法有Beyes方法[2]和神经网络方法。Beyes方法是基于统计的预测方法，但该方法需要大规模的数据来保证结果的准确性，而在实际应用中，受限于寿命预测的成本及时间。神经网络方法是通过建立网络模型及利用大量的数据对网络进行训练，从而进行预测。该方法存在易陷入局部最优解，并且隐节点的选取缺乏理论支持等缺点。

SVM方法从结构风险最小化[3]的思想发展而来，它利用核函数在高维特征空间很好地解决了小样本情况下的线性不可分问题。在SVM的基础上，将统计学习理论应用于回归和函数拟合问题，即SVR。SVR遵循SVM原则，解决了小样本、高维数、非线性以及过学习问题。SVR同样将最优分类面的求解转化为凸二次规划的求解问题。其思想是首先求得样本所确定输入与输出之间的映射关系,然后根据映射求得未知样本的取值。

在训练过程中的参数选择方面，本文结合了遗传算法，利用该算法对核函数参数进行寻优，利用最优核函数参数建立回归模型，从而提高了元器件寿命预测精度。

1 加速寿命试验

加速寿命试验是指将元件或产品置于高于正常应力条件下，促使其在短时间之内失效，然后利用失效规律预测元件或产品在正常条件下的可靠性。其原理是高应力水平下与正常应力水平下器件退化方式相似。常用的方法是在高温、加压、大功率条件下使元件加速失效，这样就可以在较短时间内通过高应力试验来推算元件在正常应力水平下的可靠性。加速寿命试验缩短了试验周期，节省了样品和费用。

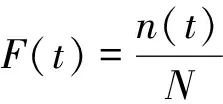
为了能够准确地推算出正常应力水平下电子元器件的寿命特征，加速寿命试验通常要进行几个等级应力水平的试验，即为加速应力的水平数。在本文中，采用多个恒定应力来进行加速寿命试验，且每次试验样本的个数相等，其中在本次试验中，应力水平数为6。

2 遗传算法SVM原理

2.1 SVM原理

支持向量机从线性可分下的最优分类超平面开始研究，最优分类面是指分类面不仅能将2个类正确分开，还能使其数据点间隔最大。它比较好地实现了结构风险最小化的思想。

假定n个维数为d的样本，则可表示为(xi,yi),x∈Rd, yi∈{+1,-1},i=1,2,…,n,如果存在一个超平面H∶w·x+b=0使各类样本正确区分，则最优超平面得满足以下条件：

(1)

(2)

式中:w为权向量，ξi≥0为误差变量，C为优化惩罚参数，b为偏置，φ(xi)为核函数，它实现了从低维空间到高维空间的映射，从而将非线性问题转换为线性分类。根据(1)式和(2)式建立拉格朗日函数：

(3)

在(3)式中，αi为拉格朗日乘子。为了求Largrange函数的最小值，则需要对w,b,ξi求偏导，并令等式为零，得出：

(4)

根据Mercer条件，将内积[5][φ(xi)·φ(xj)]用核函数K(xi,xj)来表示，因此，可将原问题转化为对偶问题,从而避免了维数灾难，表达式即为：

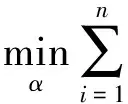
(5)

(6)

经过求解，可以得出最优分类函数为：

(7)

本文选用径向基函数(RBF)为核函数，其表达式为：

K(xi,xj)=exp{-‖xi-xj‖2/2σ2}

(8)

在(8)式中σ为核函数的宽度参数。

2.2 遗传算法参数寻优

遗传算法[6]属于进化算法，把将要解决的问题模拟成一个生物进化的过程，通过复制、交叉、突变等操作产生下一代的解，并适应度低的解将被淘汰掉，将适应度高的解保存下来。遗传算法根据所制定的适应度规则，将由个体组成的群体通过选择、交叉、变异生成最大适应度个体。遗传算法减少了陷入局部最优解的风险，并且具有良好的鲁棒性。

在SVM算法中，为了使预测结果具有更高的精确度，在对样本进行训练之前，则需要对某些参数进行优化。由SVM算法的具体步骤可知，如果选择径向核函数(RBF)为核函数，则需要对核函数的宽度参数σ以及优化惩罚参数C做出寻优，其具体步骤是：

Step1 对参数σ和C进行二进制编码，产生初始种群。

Step2 将个体进行解码，得到σ和C的值。

Step3 将参数带入SVM模型进行训练，计算实际值和预测值的均方误差，判断是否满足终止条件。若满足，则转到步骤5，若不满足，则转到步骤4。

Step4 通过选择，交叉，变异产生新一代种群，再转到步骤2。

Step5 得到最优参数组合σ和C。

3 电子元器件加速寿命试验

在此次加速寿命试验中，采用nMOSFET为测试元件。该元件采用0.6 μm工艺，栅氧化层厚度为12.5 nm，宽长比为W/L=20/0.6。

对于MOS器件，由于沟道存在热载流子[7]，将产生热载流子陷阱(氧化层陷阱、界面陷阱)效应，这些效应会导致器件特性的退化。由于温度和漏源电压是影响MOS管热载流子的重要因素，因此将温度和电压作为加速变量，并进行6个水平数的恒定应力加速寿命试验。

在本次试验中，S1应力水平下选取20个样本，其他应力水平下各选取10个样本。试验中应力水平值如表1所示。

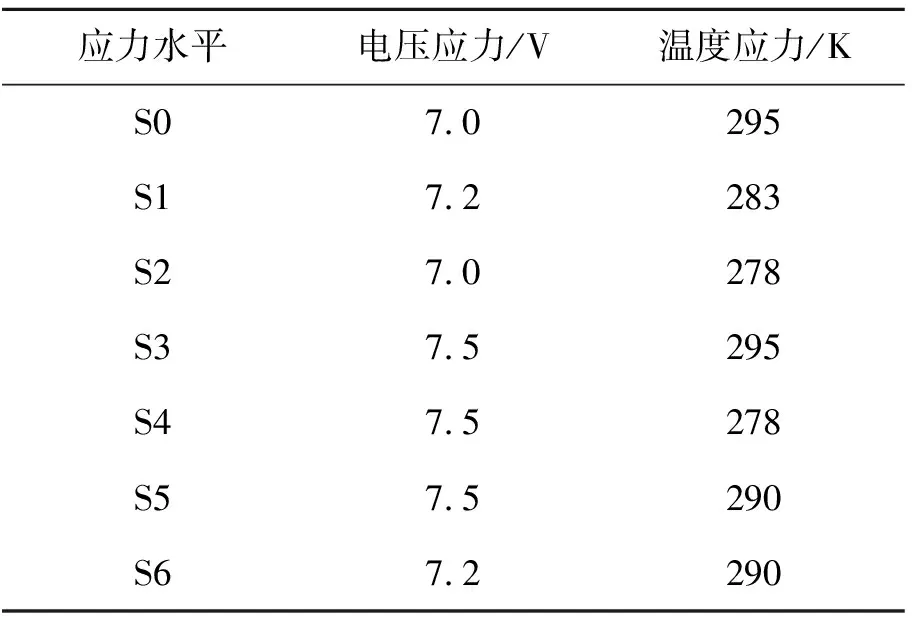
表1 应力水平示意图

在表1中，S0是指正常应力水平，S1～S6指在温度和电压应力下的加速应力水平。温度越低[8],沟道热电子退化越严重。这是因为SiO2层中有效的陷阱密度是温度的函数,当温度越高时,电子平均自由程度下降，因而俘获热电子的机率越小,热载流子注入效应减弱。再者，增加漏源电压VDS可以增加沟道热载流子效应,从而加剧热载流子退化。因此，选择低温环境和高于正常VDS的电压分别作为温度和电压加速应力，加寿命试验步骤如下:

Step1 首先挑选合格的nMOSFET并对其进行未加应力的初始测试，用于确定试验所加的应力条件。

Step2 对nMOSFET施加加速应力，加快元件的失效速度，此nMOSFET的漏源电流IDS减小，并将漏电流变化10%作为失效标准。

Step3 每个应力周期后测试并记录元件的相关数据，根据数据分析热载流子陷阱效应，提取相应的退化参数，根据退化量与应力时间的关系特性得到器件的寿命值。

在每一组应力水平下，样本的数目为10，求得元件累积失效概率，进而得到元件的可靠度。可靠度函数R(t)可表示为:

(9)

在本试验中，N的值为10。

4 元器件寿命预测

对于应力水平S1～S6，在求得累积失效概率后，根据(9)式可得不同应力水平下的可靠度。如图1所示。

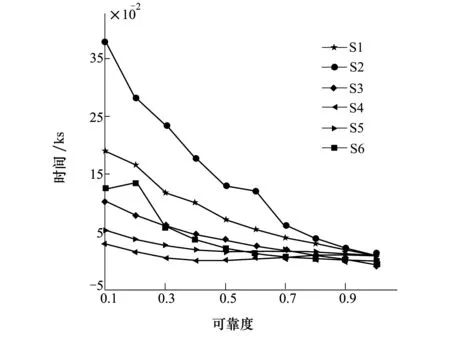
图1 可靠度-时间曲线

在获得所需的数据之后，要利用样本建立SVM回归模型，在同一综合应力水平下元器件的寿命预测中，选取应力S1进行实验。在S1应力水平下,将样本数目增至20，选取前15个样本为训练样本，并利用这些样本来建立SVM回归模型，其余5个为测试样本。对于多应力水平试验，选取S1～S6以及相应的可靠度作为输入样本，进行SVM训练，并预测正常应力下元件的寿命。具体实验步骤如图2所示。

图2 寿命预测试验步骤

对于S1应力下的寿命预测，按照图2的步骤建立起SVM回归预测模型，然后利于测试样本验证模型的精确度，并将所得结果与神经网络预测数据相比较，如图3所示。

S1应力下，SVM方法与神经网络方法预测的具体数值如表2所示。

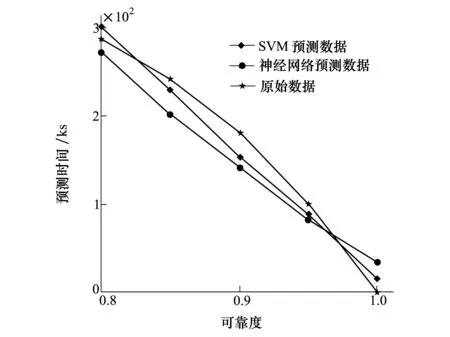
图3 S1应力下可靠度-时间曲线

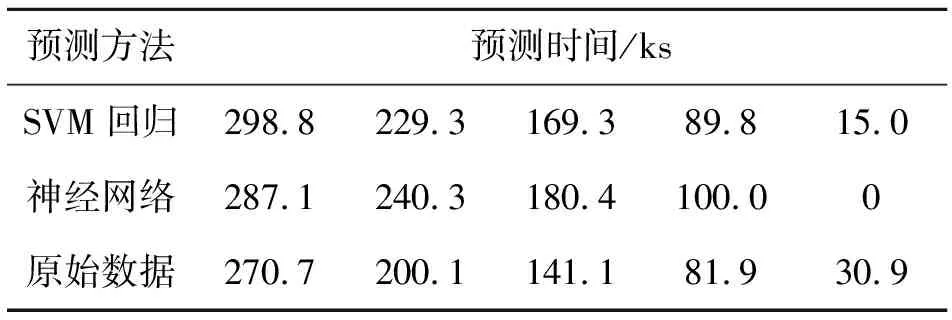
表2 S1应力下预测时间比较

由仿真结果可知，SVM预测的平均绝对误差为6.05%,神经网络预测的平均绝对误差为12.46 %，且 SVM方法在各个预测点的误差均在10%左右。试验结果表明，SVM方法具有很好小样本学习能力，因此相对于神经网络，其具有更高的预测精确度。在本文中，将遗传算法应用于SVM的参数寻优中，其预测结果更接近于真实值。

对于多应力水平试验，将加速应力水平S1～S6及相应的可靠度作为训练模型的输入，并将元件的寿命数据作为模型的输出，以此来建立SVM的回归模型。然后利用该模型进行正常应力水平下的寿命预测。

在参数寻优阶段，利用遗传算法得到最优的核函数的宽度参数 以及优化惩罚参数 。设置最大迭代代数为100，群体规模为20。经过遗传算法寻优，得出惩罚因子C=47.665 5，径向基核函数的宽度参数σ=0.350 95。

在得到最优参数σ和C后，将其带入SVM进行训练，并将训练好的模型进行寿命预测。预测结果同神经网络预测结果比较如图4所示。

其中，SVM方法预测结果的具体数值如表3所示。

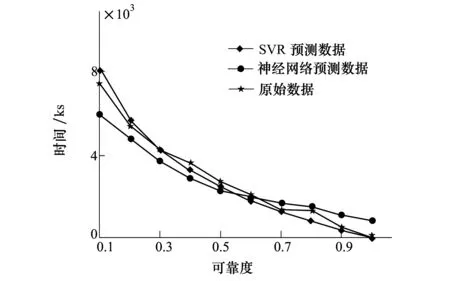
图4 正常应力下可靠度-时间曲线

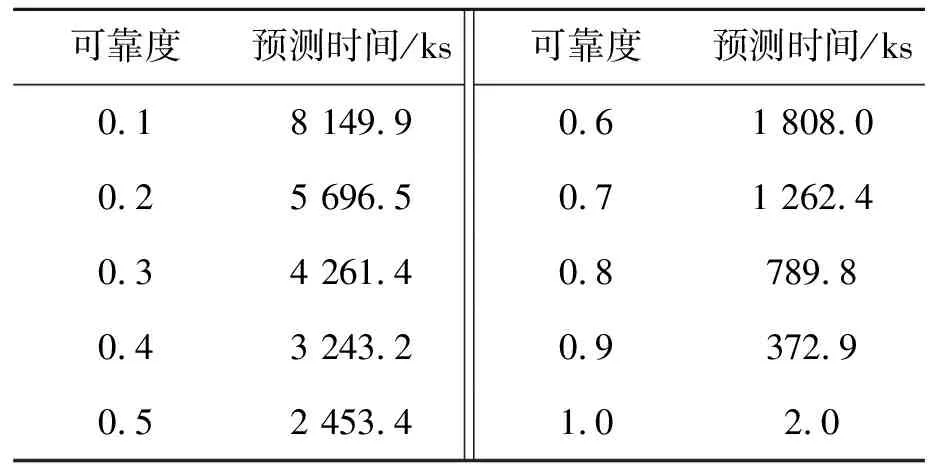
表3 多应力条件下SVM方法预测时间

经过仿真比较，得出遗传算法SVM的预测模型对预测样本预测的平均绝对误差为8.6%，神经网络的预测模型的平均绝对误差为22.65%，SVM方法预测结果的误差明显小于神经网络预测结果的误差。这是由于神经网络以经验风险最小化原则为基础，对于预测结果的精确度依赖于样本的数量和质量，易出现过学习现象，并且需要多次相应可调参数的修正和网络性能测试，才能得到一个较好的神经网络模型，但是SVM方法能够很好地解决有限样本的高维模型构造问题，因此具有更好的泛化能力。

实验表明，基于遗传算法SVM的寿命预测模型能够合理地学习MOS 管的寿命失效规律，尽管不能给出失效规律的显示模型，但仍然可以对寿命进行有效预测。

5 结 论

本文将SVM方法应用在元器件的寿命预测方面。选择nMOSFET为试验元件，由于热载流子效应会引起MOS管的特性退化，因此选择温度及漏极电压作为加速应力来促进热载流子效应，因而使元件加速失效。在得到相应应力水平下的寿命时间后，计算出元件的可靠性水平，利用应力水平及可靠性建立SVM回归模型，并在参数寻优的过程中结合遗传算法，以确保预测的精确度。试验结果表明，多种失效机理同时存在的情况下，遗传算法SVM在小样本情况下能够很好地预测元件正常应力下的失效时间。因此，本文方法在元器件的寿命预测方面具有实际指导作用。

参考文献：

[1] Lawless J F. Statistical Models and Methods for Lifetime Data[M]. 2nd Edition. New York: Wiley, 2003

[2] 邹心遥，姚若河. 基于 LSSVM 的小子样元器件寿命预测[J]. 半导体技术，2011, 9(36): 730-733

Zou Xinyao, Yao Ruohe. Life Prediction of Electronic Components with Small Sample Based on LSSVM[J]. Semiconductor Technology, 2011, 9(36): 730-733 (in Chinese)

[3] 胡小平, 韩泉东，李京浩. 故障诊断中的数据挖掘[M]. 长沙：国防科技大学出版社，2009

Hu Xiaoping, Han Quandong, Li Jinghao. Data Mining in Fault Diagnosis[M]. Changsha: National University of Detence Technology Press, 2009 (in Chinese)

[4] Zhang L F, Xie M, Tang L C. A Study of Two Estimationapproaches for Parameters of Weibull Distribution Based on WPP[J]. Reliability Engineering & System Safety, 2007, 92(3): 360-368

[5] Michiel D, Mia H, Suykens J A K. Model Selection in Kernel Basedregression Using the Influence Function. Journal of Machine LearningResearch, 2008, 9(11): 2377-2400

[6] 戴上平，宋永东. 基于遗传算法与粒子群算法的支持向量机参数选择[J]. 计算机工程与科学, 2012, 10(34): 113-116

Dai Shangping, Song Yongdong. Parameter Selection of Support Vector Machines Based on the Fusion of Genetic Algorithm and the Particle Swarm Optimization[J]. Computer Engineering & Science, 2012, 10(34): 113-116 (in Chinese)

[7] 李春，邸曼丽. 故障预测技术在半导体设计中的应用[J]. 半导体技术，2009，3(32)：280-282

Li Chun, Di Manli. Application of Prognostic Technology in IC Design[J]. Semiconductor Technology, 2009, 3(32): 280-282 (in Chinese)

[8] 洪根深，肖志强，王栩，周淼. 0.5 m部分耗尽SOI NMOSFET热载流子可靠性研究[J]. 微电子学，2012，2(42)：293-296

Hong Genshen, Xiao Zhiqiang, Wang Xu, Zhou Miao. Study on Hot Carrier Reliability of 0.5 m PD SOI NMOSFET[J]. Microelectronics, 2012, 2(42): 293-296 (in Chinese)