图像处理的非线性扩散方法

（海军装备研究院航空装备论证研究所，上海200436）

非线性扩散是图像平滑的重要方法，而图像平滑在图像处理和计算机视觉中是一个基本问题。这主要因为平滑可以起到2个重要作用：一是图像邻域信息的交互，因而可以扩大局部数据的影响；二是平滑具有正则化的作用，可以将一个没有唯一解的病态问题转化为良态问题。另外，非线性扩散还可以应用在光流分析和几何活动轮廓模型中。最普通的平滑方法是将数据与Gaussian 核进行卷积[1]，也就是通常所说的线性平滑。线性平滑实现简单，计算效率高，而且可扩展到多维数据或矢量型、矩阵型数据。然而，近年来非线性扩散越来越引起研究者的注意，并且在许多应用领域替代了Gaussian 平滑。这主要因为非线性平滑具有保持数据不连续性的能力，避免了Gaussian平滑的模糊效应。

本文拟针对非线性扩散方法进行总结和分析：首先，介绍了非线性扩散的物理基础及数学性质；然后，介绍了非线性扩散方法在图像处理领域的分类及相关研究成果；最后，指出非线性扩散方法的研究趋势。

1 非线性扩散原理

非线性扩散是以日常生活中都能观察到的扩散现象为物理背景的，例如热量的扩散、2种不同液体自然混合时发生的扩散等等。

当观察大量粒子扩散时，可把粒子的浓度c(r,t)作为位置r 和时间t的函数来描述；当追踪一个粒子的移动时，作为随机过程，可以考虑这个粒子在时刻t 出现于位置r的概率密度p(r,t)，这2种情况都遵守方程

式中，Δ代表散度。

方程（2）称为扩散方程，D为扩散系数，j是与浓度梯度成正比的粒子流或概率流，即Fick 定律，扩散系数D 由扩散粒子的性质、扩散粒子与介质粒子的相互作用以及温度等决定。

扩散方程主要基于2个原则：浓度差异的平衡和质量守恒定律。浓度差异的平衡由Fick定律来体现，而质量守恒描述为

综合式（2）、（3），就得到扩散方程（1）。

连续情况下，扩散方程（1）主要具有以下性质[2]：

2）极值原理。令a:=infΩf，b:=supΩf，则在Ω×(0,∞)上，a≤u(x,t)≤b；

4）Lyapunov 函数。对任意凸性函数r ∈C2[a,b]，为Lyapunov函数且为以为下界的单调递减函数；

5）收敛性。在Lp(Ω),1≤p＜∞范数意义下，为灰度均值。

2 非线性扩散在图像处理领域中的分类

在图像处理中，扩散模型可用于图像的平滑处理。在扩散过程中，灰度值在图像中传播，当所有像素的灰度值相等时达到平衡。与质量守恒相对应的是，图像的灰度均值不变。灰度扩散的方式取决于扩散系数矩阵D，根据D的不同，可以分为3种：①均匀扩散。D为单位矩阵；②各向同性扩散。D为一个带有尺度因子的单位矩阵，其尺度因子由图像的局部结构决定；③各向异性扩散。D为任意一个由图像局部结构决定的对称正定矩阵。

2.1 标量的非线性扩散

几乎所有的非线性扩散方法都以Perona-Malik[3]的研究工作为基础。Perona-Malik首先提出了对灰度图像进行各向异性扩散滤波的P-M模型，其主要思想是将非线性扩散的程度同图像内容相联系，把图像平滑转化为对偏微分方程的求解，对区域内和区域间采取不同的滤波策略，减少对图像特征的平滑。

Perona-Malik提出的扩散方程为

式中：u代表恢复图像；Δ代表散度；g为扩散函数；∇u为u的梯度，初始化条件为u(x,0)=f(x)，f(x)为原始图像，定义域为Ω:(0,∞)。

常用的扩散函数有以下2种[3]。

Perona-Malik Ⅰ：

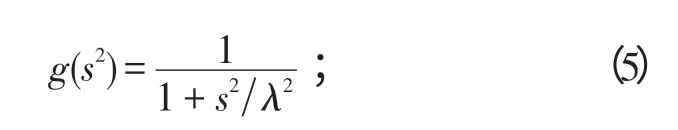
Perona-Malik Ⅱ：

Charbonnier的扩散函数不同于其他的函数的是，它不允许后向扩散，因而只保留边缘而不能增强边缘。Weickert的扩散函数的特点是比Perona-Malik的扩散函数下降的更快。

2.2 张量的非线性扩散

每每谈到图像，首先想到具有二维结构的数组，这种结构在灰度图像中非常普遍。但是二维结构不是一定的，例如：视频序列是三维结构的，尤其在多媒体应用领域，图像数据都是多维的。图像数据也不一定是标量数据，例如：对于一幅彩色图像，每一像素都由一个颜色矢量表示，因而是矢量数据；在医学图像处理领域，还有DT-MRI图像，每一像素都由一个矩阵表示，因而是矩阵数据。除此以外，还有对由输入图像产生的矩阵类型的数据进行平滑处理的实际需求，经常使用的结构张量[6]就是从图像梯度得出的矩阵类型的数据。在图像处理中有时也需要对这种矩阵类型的数据进行平滑处理。Tschumperlé和Deriche[7]将非线性扩散滤波技术扩展到对矩阵类型数据的处理。

对矩阵类型的数据进行扩散的最直接方法就是分别平滑矩阵的各个分量。分别平滑各个分量的方法参见文献[6，8]，其中，文献[6]的扩散是线性的，而文献[8]的扩散是非线性的。实际上，对于均匀扩散（或高斯平滑）而言，这是一个比较合适的方法。但对于非线性扩散（包括各向同性和各向异性），这种方法会产生问题：如果分别对各分量进行扩散，可能会在不同的位置产生不同的结构，例如，对于一幅彩色图像，边缘位置可能被不同的颜色值定位到不同的地方。

解决这一问题的方法是使用共同的扩散矩阵来耦合各个分量的信息，共同的扩散矩阵由所有分量的数据信息决定，这一点通过对所有分量的梯度信息求和作为扩散函数的自变量来实现。使用共同的扩散矩阵来耦合各个分量的信息的方法始于文献[7]的工作，其扩散方程如下：

式中，ui,j(i=1,2,…,n;j=1,2,…,m)为张量的分量。

式（9）的扩散是各向同性扩散，其扩散系数是一个标量。各向异性的非线性滤波方程为

对矩阵数据进行非线性扩散的应用之一就是对结构张量进行处理。传统的线性滤波方法处理的结构张量简称为线性张量，而非线性扩散产生的张量简称为非线性张量。

由式（9）、（10）可以看出对张量数据的非线性扩散滤波和对标量数据进行非线性滤波的计算过程是一样的，只是把张量的各分量看成不同的信息通道，然后综合各通道的数据信息计算扩散系数矩阵作为各信息通道共同的扩散系数矩阵。

3 研究趋势分析

1）如何解决平滑去噪和保留图像特征点之间的矛盾。为增强边缘，非线性扩散在其最初的设计中保留了2个问题：一是缺乏连续意义下一般的扩散函数理论；二是没有考虑噪声和边缘的区别。这些问题可以通过平滑或者在计算梯度之前对u 进行平滑处理来解决[9]。

改进后的扩散方程为

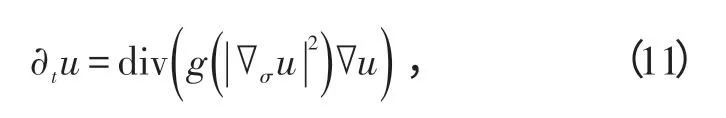
式中，∇σu=∇()

Kσ∗u。须指出的是，这一预平滑处理对没有后向扩散的扩散函数不是必要步骤，也并没有完全解决平滑去噪和保留图像特征点之间的矛盾。如何解决好这一矛盾，是非线性扩散方法有待解决的主要问题之一。

2）结构的封闭性问题。由于非线性扩散方法可以促进图像邻域信息的交互，因而这种方法还可在一定程度上修补一些缺失的结构，使得没有任何结构特征的小块图像区域被其邻域的结构特征所填充，并且可用参数控制填充的尺度。如何更好地实现这一功能以及参数设置等问题都是值得深入研究的。

3）不连续点的保留。非线性扩散方法相对于线性扩散方法的最大优势在于它能够在一定程度上控制在不同区域的扩散程度，以避免过度平滑而使一些特征点丢失。在非线性扩散的过程中，图像取向和灰度幅度等特征的不连续点都应该被保存，最好是非线性扩散的参数可同时控制某一特征不连续点是否应该保持，这有可能需要多尺度分析，以达到在保留不连续点的目的。做到这点也有利于形成封闭的结构。

4）简化参数设置，并提高其鲁棒性。这点很容易理解，也是很多算法追求的目标，即应引入尽量少的参数，并使参数不会受输入数据的微小变化的影响。

[1]GRUNBAUM B，SHEPHARD G.Patterns on the 2-sphere[J].Mathematicka，1981，28（1）：1-35.

[2]WEICKERT J.Applications of nonlinear diffusion in image processing and computer vision[J].Acta Mathematics University Comenianae，2001（1）：33-50.

[3]PERONA P，MALIK J.Scale space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Inteligence，1990，12（7）：629-639.

[4]WEICKERT J.Scale-space properties of nonlinear diffusion filtering with a diffusion tensor[R].Kaiserslautern：University of Kaiserslautern，1994.

[5]CHARBONNIER P，BLANC-FÉRAUD L，AUBERT G，et al.Two deterministic half-quadratic regularization algorithms for computed imaging[C]//Proceeding of IEEE International Conference on Image Processing.1994：168-172.

[6]WESTIN C，MAIER S E，KHUDHIR B，etal.Image processing for diffusion tensor magnetic resonance imaging[C]//Medical Image computing and Computer-assisted Intervention.Berlin：Springer，1999：441-452.

[7]TSCHUMPERLÉ D，DERICHE R.Diffusion tensor regularization with constraints preservation[C]//Proceeding of 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.2001：948-953.

[8]HAHN K，PIGARIN S，PUTZ B.Edge preserving regularization and tracking for diffusion tensor image imaging[C]//Medical Image computing and Computer-assisted Intervention.Berlin：Springer，2001：195-203.

[9]CATTE F，LIONS P L，MOREL J M，et al.Image selective smoothing and edge detection by nonlinear diffusion[J].SIAM Journal on Numerical Analysis，1992（32）：1895-1909.