一种新的基于Graph cuts方法的SAR图像分割模型

刘光明，孟祥伟，杨祥红，程 焕

（1.海军航空工程学院a.青岛校区，山东青岛266041；b.电子信息工程系；c.军事教育训练系，山东烟台264001；2.91967部队，河北沙河054102）

Graph cuts方法[1]是一种快速优化技术，有效解决计算机视觉的低层次问题，如表面重构、分割、去噪等问题。其优点是迭代计算的高效性和能得到全局最优解。其缺点在于精度限于像素精度和只能用各项异性算子AO（Anisotropic Operators），不能用各项同性算子IO（Isotropic Operators）。Graph cuts方法是计算1个图（Graph）中的最大流的方法，等价于最小割。在图像处理问题中，图是指像素网络，而割（Cut）表示轮廓。图像去噪、图像分割等问题的能量全局最优解都可以通过求解图的最大流或最小割问题来准确地实现。Graph cuts方法定义在最大后验-马尔科夫随机场框架，是一种比模拟退火快的离散优化技术。近年来，国际上用Graph cuts方法进行图像分割处理的研究也很深入，发表了大量的研究成果。本文对Ayed等人[2]提出的SAR图像水平集分割模型采用Graph cuts方法优化处理，充分利用Graph cuts方法的优点，只须几次迭代算法就可收敛，表明了算法的有效性。

1 最大流/最小割模型

在1个有向图中，只有出去的边没有进来边的节点叫做源节点s（source），只有进来的边没有出去的边的节点叫做汇节点t（sink），其他的节点进来的边和出去的边应该是平衡的，见图1所示。边上有加权值，假设对于一个交通图来说，可以认为边上的权重为一条道路上的最大流量。对于图中任意2个节点来说，它们之间可以存在很多路径，每条路径上可以承载的最大流量取决于这条路径上权重最小的那条边所能承载的流量，而所有路径上所能承载流量之和就是这2个节点之间能通过的最大流。任一网络图（Graph）中，最大流的流量=最小割集的割量。

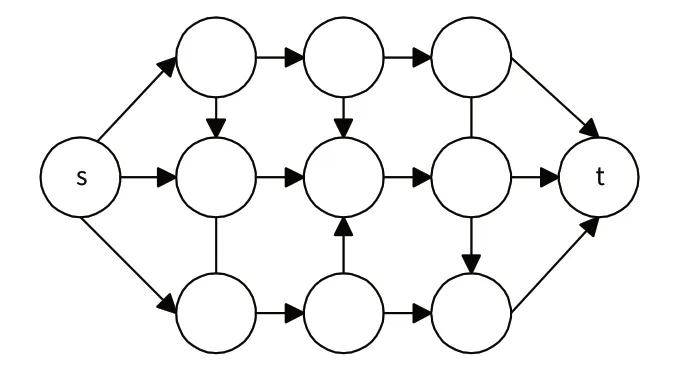
图1 有向图网络Fig.1 Directed graph

假设G=(V,E)是1个包含1个顶点集v ∈V 和1个边缘集e ∈E ⊆V×V的图。V 包括离散图像的所有节点和2个终端，即1个源节点s 和1个汇节点t，其余均为中间节点。E 包括图像节点邻域系统的所有连接（如4-连接或8-连接，见图2所示），类似源节点s 或者汇节点t 与每个图像节点u ∈V/{s,t}的连接。对E 中的每条边均有权w(eij)＞0（简记为wij，称为边容量），则称这样的赋权有向图G为容量网络，记为G=(V,E,w)，通过G 中边eij的流量pij，可称为边eij的流量。所有边上流量的集合p={pij}可称为该网络G的1个流。

图2 图像邻域Fig.2 Image neighborhood

对于1个图中的2个节点来说，如果把图中的一些边去掉，刚好让它们之间无法连通，这些被去掉的边组成的集合就叫做割，最小割就是指所有割中权重之和最小的1个割。

最大流/最小割定理（max flow/min cut theory）：对于任意1个只有1个源点和1个汇点的网络图来说，从源点到汇点的最大流等于最小割，见图3所示。

图3 流图Fig.3 Flow configurations

1）连续最大流模型[3]。

式（1）中：Ω为图像域；div(∙)是散度符号；ps(x)是从源点s 到点x的源流量；pt(x)是从汇点t 到点x的汇流量；p(x)是空间流量；Cs(x)、Ct(x) 和C(x)分别是与ps(x)、pt(x)和p(x)对应的约束能量。

引入函数r（对偶变量），式（1）可以转化为与其等价的Prime-dual模型[4-5]：

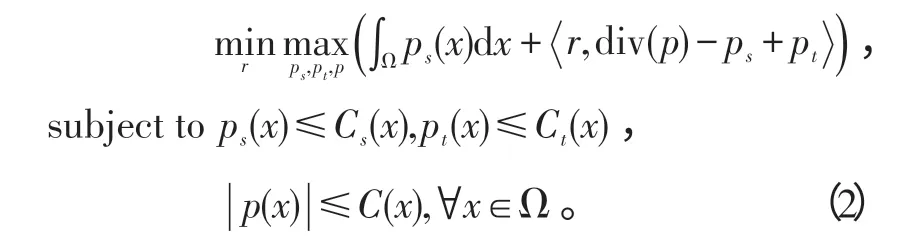
2）连续最小割模型[4-5]。

对于1个图，1个“s-t”割分割V为2个子集，即：

式（3）中：Vs包含源点s；Vt包含汇点t。

令C(e)≥0为与每个边缘e ∈E 有关的值。每个s-t 割的能量是所有边缘值C(e)之和，其中e ∈Est⊂E连接2个节点，1个在Vs中，1个在Vt中。最小割在于找到最小能量“s-t”割，即：

2 基于Graph cuts的活动轮廓模型

Graph cuts方法可以计算如下形式离散能量的精确解：

式（5）是一类一阶各向异性离散二进制能量，其中，θ ＞0 和μ ＞0是系数；表示长度，表示面积。对任意(s,t)，一个次模（submodular，即最优化条件）能量满足下式：

式（6）表明正则化项R是两两相互作用（3个节点间不允许有相互作用）的。

Graph cuts方法可近似求得式（7）表示的连续几何问题的全局解为

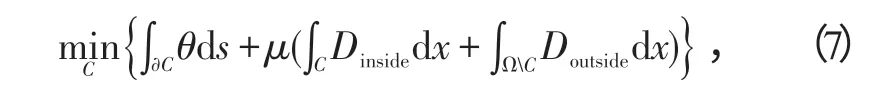
式中：C为边缘曲线；∫∂Cθds表示周长；∫CDinsidedx 和∫ΩCDoutsidedx分别表示内部、外部面积。

式（7）的近似式为

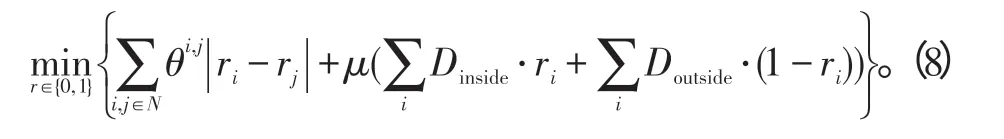
可以看出式（8）满足次模条件。因此，Graph cuts方法可以确保取得全局最优解。

3 提出的新模型

Ayed等人提出模型[2]的能量泛函可以用变分水平集[6-10]表示为

式（9）中：ϕ是水平集函数[6]；M1=H(ϕ)；M2=1-H(ϕ)；ε是较小的整数；μ ＞0。

由于水平集演化方程的复杂性，还会造成计算效率较低，很难满足实时性要求。Graph cuts方法是一种快速优化技术，其优点是迭代计算的高效性和能得到全局最优解。下面基于Graph cuts方法对方程（9）进行变换，提出图像分割新的模型。

将图中的节点与图像像素相联系，像素集的积分可以被表示为一个N×1的链向量，其定义为：

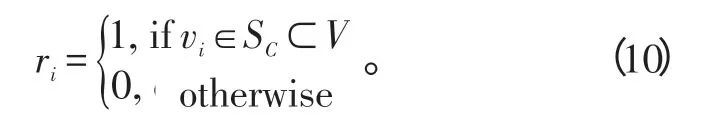
定义：

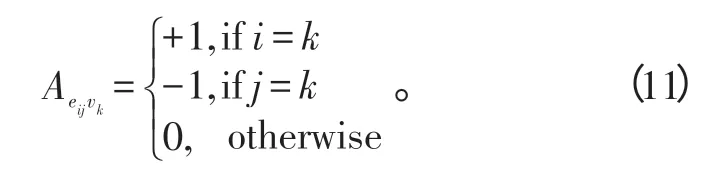
对于每个顶点vk和边缘eij，其中eij可以任意分配方向。式（9）在图（Graph）上的对应项可以简单表示为：

对式（12）中含C1和C2的部分分别写为：

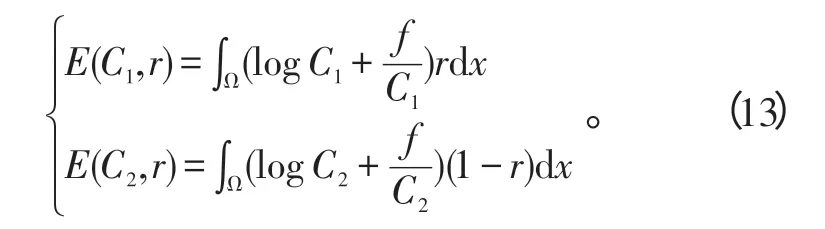
对式（13）关于C1和C2分别求偏导数，可得到：

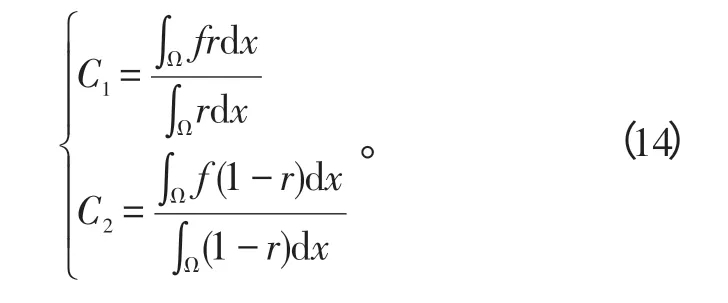
用求和形式，式（12）可写成一个简化的最大流/最小割计算问题：

将本文提出的新模型简记作GC_Ayed。

算法步骤总结如下：

1）初始化C1，C2和r；

2）求式（14）得到C1，C2；

3）求式（15）中的最大流/最小割得到最有轮廓r；

4）重复步骤2）～3）直到轮廓位置保持不变为止。

4 数值实验与分析

采用2幅实测Envisat SAR图像来验证和分析提出模型的分割性能，见图4。2幅实测SAR图像的尺寸分别为179×205 和250×250，灰度范围为0～255。本文实验是在CPU为AMD 1.8 GHz、内存为1 GB的硬件环境以及windows XP SP2的软件环境下，采用Matlab 编程实现。将本文提出的GC_Ayed模型、与Ayed模型进行比较，验证本文提出模型的有效性。

图4 实测SAR图像Fig.4 Real SAR images

对于SAR图像，本文采用一种区域内部均匀性度量的方法来评估。根据图像分割的定义，分割后图像每个区域内部应该是均匀的，不同区域之间存在较大的差异，所以区域内部的均匀程度表征了图像分割的质量。定义分割精度度量[11]如下：

式（16）中：Ai为图像中的不同分割区域；C为归一化系数；f(x)为图像中点x 处的灰度值；ni为区域Ai中的像素个数；pp值越接近于1，表明分割图像内部各区域越均匀，图像的分割质量越好。

从图5可看出，本文提出的GC_Ayed模型能准确地分割SAR图像1中的水域，而Ayed模型不能完整地分割出水域边缘轮廓。从图6可以看出，GC_Ayed模型也能准确地提取SAR图像2中的机场道路边缘，而Ayed模型分割效果较差。从表1、2可看出，GC_Ayed模型所需运行时间大约是基于水平集的活动轮廓模型所需时间的一半，分割精度也得到了较大的提高。

图5 SAR图像1的分割结果Fig.5 Segmentation results of SAR image 1

图6 SAR图像2的分割结果Fig.6 Segmentation results of SAR image 2

表1 运行时间和分割精度的比较（SAR图像1）Tab.1 Comparsion of running time and segmentation accuracy for SAR image 1

表2 运行时间和分割精度的比较（SAR图像2）Tab.2 Comparsion of running time and segmentation accuracy for SAR image 2

5 结论

本文利用Graph cuts方法，将基于活动轮廓模型和水平集方法的SAR图像分割模型转化成最大流/最小割问题。通过实测SAR图像的分割实验，提出的新模型所需运行时间大约是基于水平集的活动轮廓模型所需时间的一半，分割精度也得到了较大的提高。

[1]BOYKOV Y，FUNKA-LEA G.Graph cuts and efcient nd image segmentation[J].International Journal of Computer Vision，2006，70（2）：109-131.

[2]BEN AYED I，MITICHE A，BELHADJ Z.Multiregion level set partitioning of synthetic aperture radar Images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（5）：793-800.

[3]ZHU MINGQIANG，CHAN T F.An efficient prime dual hybrid gradient algorithm for total variation image[R].Los Angeles：University of California at Los Angeles，2008：1-29.

[4]YUAN JING，BAE EGIL，TAI XUECHENG，et al.A study on continuous max-flow and min-cut approache[C]//Computer Vision and Pattern Recognition.San Francisco，2010：1-22.

[5]PUNITHAKUMAR K，YUAN JING，BEN AYED I，et al.A convex max-flow approach to distribution based figure-ground separation[J].Journal on Imaging Sciences，2012，5（4）：1333-1354.

[6]STANLEY OSHER，JAMES A SETHIAN.Fronts propagating with curvature-dependent speed algorithms based on hamilton-Jacobi formulations[J].Journal of Computational Physics，1988，79（1）：12-49.

[7]MUMFORD D，SHAH J.Optimal approximation by piecewise smooth functions and associated variational problems[J].Communications on Pure and Applied Mathematics，1989，42（5）：577-685.

[8]TONY F CHAN，LUMINITA A VESE.Active contours without edges[J].IEEE Transactions on Image Processing，2001，10（2）：266-277.

[9]LUMINITA A VESE，TONY F CHAN.A multiphase level set framework for image segmentation[J].International Journal of Computer Vision，2002，50（3）：271-293.

[10]CHUNMING LI，CHIU-YEN KAO，JOHN C GORE，et al.Minimization of region-scalable fitting energy for image segmentation[J].IEEE Transactions on Image Processing，2008，17（10）：1940-1949.

[11]ROSS T D，MOSSING J C.The MSTAR evalution methodology[C]//Proceeding of SPIE.1999：705-713.