载体角运动对旋转捷联惯导误差的影响分析
(海军航空工程学院控制工程系,山东烟台264001)
惯性导航系统(Inertial Navigation System,INS)具有工作自主性强、提供导航信息较为全面、抗干扰能力强、适用条件宽等独特优点,但也存在定位误差随时间累积的缺陷,而通过旋转调制等系统误差自动补偿技术可以较好地提高惯导系统的精度[1]。旋转调制误差补偿技术的基本思想是将惯性元件漂移等误差量通过旋转机构调制成某种周期变化的形式,在导航解算过程中利用积分运算自动将误差平均抵消。
目前,国内外众多科研机构和学者对基于旋转调制方法的捷联惯导误差自动补偿技术进行了大量的研究[2-4],部分成果也得到了初步应用。在众多的研究中,针对旋转捷联惯导系统(Rotating Strap-down INS,RSINS)原理和静态导航误差的分析较多[5-6],关于动态环境对误差补偿效果的影响却鲜有讨论。针对单轴旋转方案,通过建模和仿真专门分析了载体角运动对旋转调制误差补偿效果的影响。结果表明:载体特定的连续角运动状态对旋转捷联惯导的误差补偿有一定影响,且在正反转停方案中,这种影响相对较小。
1 旋转捷联惯导误差补偿原理
在捷联式惯导系统中,旋转调制误差自动补偿技术在本质上是通过周期性地改变姿态矩阵,使系统中缓慢变化的误差在转动周期内均值接近0,从而减小系统误差的积累,提高导航精度[7]。
旋转捷联惯导系统基本结构原理如图1所示[8]:惯性测量组合(IMU)安装在按一定规律旋转的平台上,则IMU 测得的是旋转平台相对惯性坐标系的角速度和比力信息。导航计算机接收该信息以及平台相对载体的角位置信息,完成导航解算。

图1 旋转捷联惯导系统结构原理示意图Fig.1 Schematic of RSINS framework
令旋转平台坐标系为r,假定初始时刻该平台系与载体系重合。忽略陀螺仪和加速度计安装误差,同时令r系内陀螺漂移为εi(i=x,y,z)、加速度计零偏为∇i(i=x,y,z)。当平台绕台体z轴按角速率旋转时,有
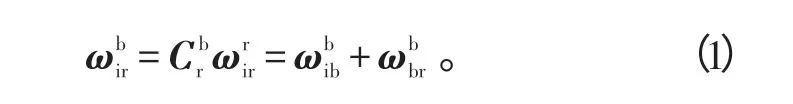
式(1)中:i表示惯性系;b表示载体系;角速度ω的下标表示相对旋转的坐标系,上标表示是在对应坐标系内的分量;Cbr是从r系到b系的变换方向余弦矩阵;


同样,可以得到:

式中,δfb是b系中表示的比力误差。
仅考虑εi(i=x,y,z)和∇i(i=x,y,z)中的常值分量,则和δfb的水平分量将以周期2π/ω 变化,在平台转动周期内其均值为0。可见,IMU的旋转可以消除敏感轴与转轴方向垂直的陀螺仪和加速度计常值误差[4],从而提高惯导输出精度。
旋转捷联惯导可以有单轴、双轴、三轴等不同方案[9-11],不同旋转方案的作用和效果有所不同,仅针对单轴旋转方案加以讨论。
2 常值角运动对惯导误差的影响分析
旋转捷联惯导本质上是通过周期性地改变姿态矩阵,使某些误差在转动周期内均值接近0 并减小系统误差累积而提高导航精度的。
当载体自身存在角运动时,姿态矩阵实时发生变化,则必然会对系统误差的旋转调制补偿过程产生影响。
2.1 单轴连续旋转方案
假定旋转捷联惯导IMU 绕平台z轴作常值连续旋转,角速率=1.5(°)/s。在此前提下,载体分别绕z轴和x轴作常值反向转动时系统导航误差如图2~4所示。其中:图2和图3分别是载体绕z轴反向转动角速率分别为3(°)/s 和1.6(°)/s时的经度误差λ、纬度误差L、东向姿态误差ϕe和东向速度误差ve曲线;图4是载体绕x轴以1.5(°)/s的角速率转动时的经纬度误差、东向姿态误差和东向速度误差曲线。
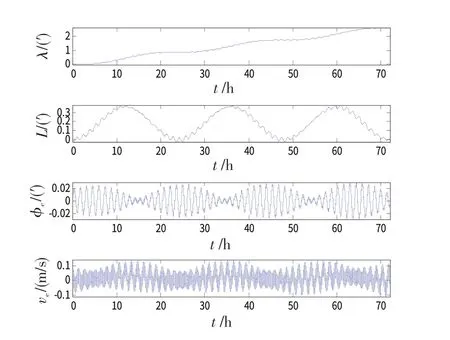
图2 载体绕z轴以3(°)/s 旋转时的惯导误差曲线Fig.2 RSINS error curves with 3(°)/s carrier rotation on z-axis

图3 载体绕z轴以1.6(°)/s 旋转时的惯导误差曲线Fig.3 RSINS error curves with 1.6(°)/s carrier rotation on z-axis

图4 载体绕x轴以1.5(°)/s 旋转时的惯导误差曲线Fig.4 RSINS error curves with 1.5(°)/s carrier rotation on x-axis
由图2、3可以看出,当IMU 绕平台z轴连续旋转且当载体绕z轴存在角运动时,导航精度与载体反向转动角速率有关:该角速率与的差值越小,则对纬度误差、水平姿态误差和水平速度误差的影响越严重;当该角速率与接近时,IMU 绕平台的旋转补偿作用几乎被抵消,纬度误差、水平姿态误差和水平速度误差甚至增大了。而从图4可以看出,当载体绕与z轴相垂直的x轴旋转时,对惯导精度虽然有一定影响,但IMU旋转的误差调制补偿作用仍然有效。
2.2 单轴正反转停方案
正反转停方案是当前研究较多的单轴旋转方案,针对一种较典型的4个位置正反转/停设计讨论[4,9]。

图5 载体绕z轴以3(°)/s 旋转时的惯导误差曲线Fig.5 RSINS error curves with 3(°)/s carrier rotation on z-axis

图6 载体绕z轴以1.6(°)/s 旋转时的惯导误差曲线Fig.6 RSINS error curves with 1.6(°)/s carrier rotation on z-axis
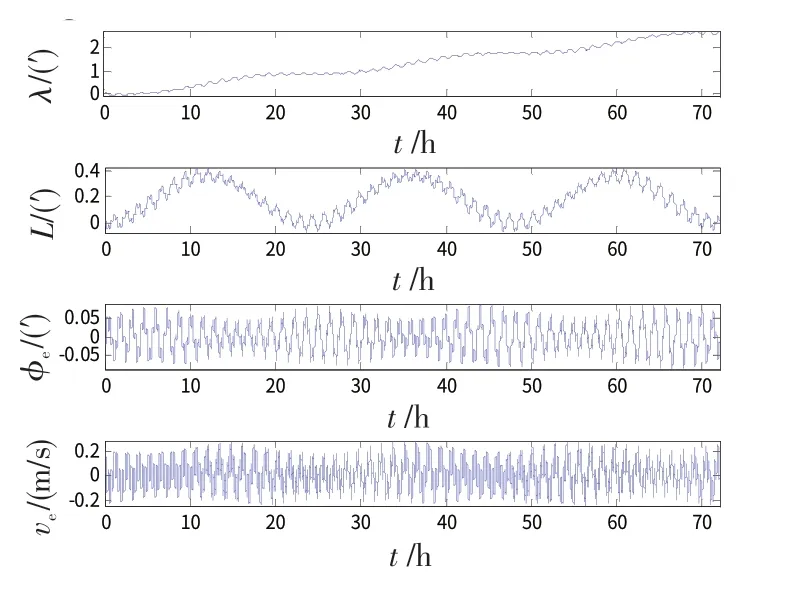
图7 载体绕z轴以1.5(°)/s 旋转时的惯导误差曲线Fig.7 RSINS error curves with 1.5(°)/s carrier rotation on z-axis
由图5~7可以看出,在IMU 绕台体z轴正反转停方案中,载体绕z轴的常值旋转对惯导精度的影响很小,或者说,系统水平误差都能够得到较好的补偿。但同时,与图2、图3比较可以发现,正反转停方案中各水平误差的补偿效果比连续旋转方案稍差。
3 周期角运动对惯导误差的影响分析
3.1 单轴连续旋转方案
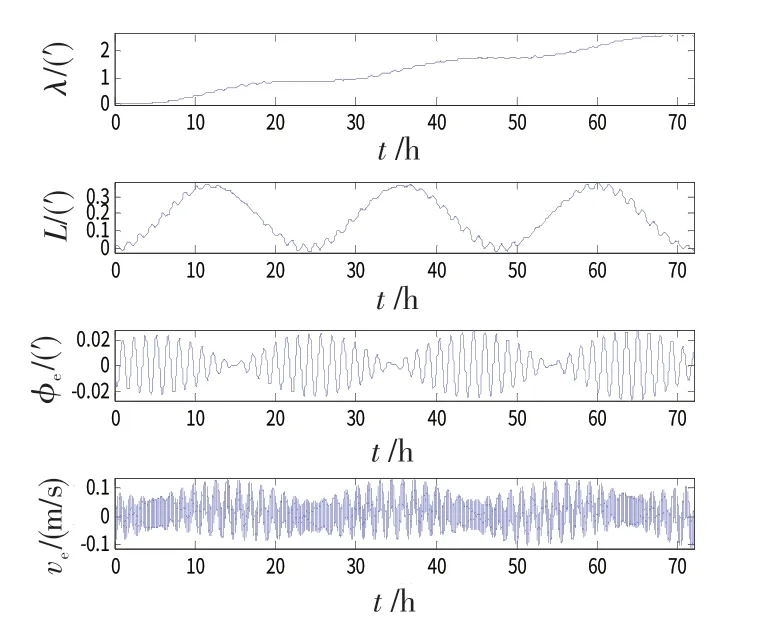
图8 载体绕z轴以1.5(°)/s(1 Hz)旋转时的惯导误差曲线Fig.8 RSINS error curves with 1.5(°)/s(1 Hz)carrier rotation on z-axis

图9 载体绕z轴以1.5(°)/s(0.01 Hz)旋转时的惯导误差曲线Fig.9 RSINS error curves with 1.5(°)/s(0.01 Hz)carrier rotation on z-axis
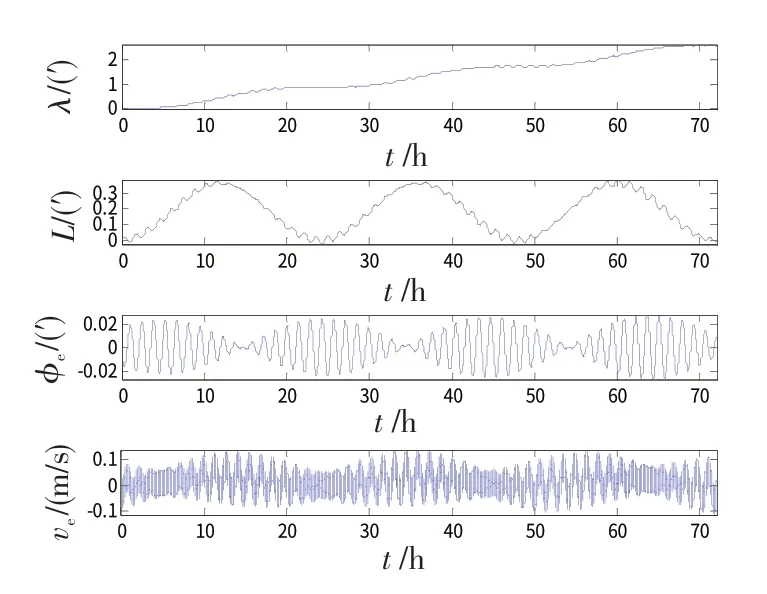
图10 载体绕z轴以0.5(°)/s(0.01 Hz)旋转时的惯导误差曲线Fig.10 RSINS error curves with 0.5(°)/s(0.01 Hz)carrier rotation on z-axis
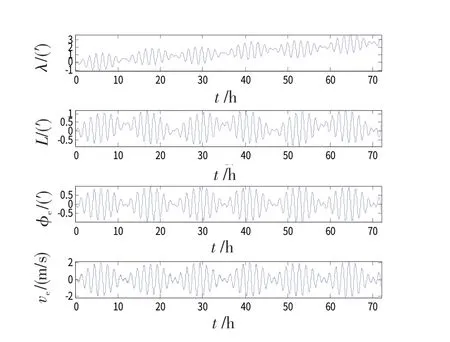
图11 载体绕z轴以4.5(°)/s(0.01 Hz)旋转时的惯导误差曲线Fig.11 RSINS error curves with 4.5(°)/s(0.01 Hz)carrier rotation on z-axis
3.2 单轴正反转停方案
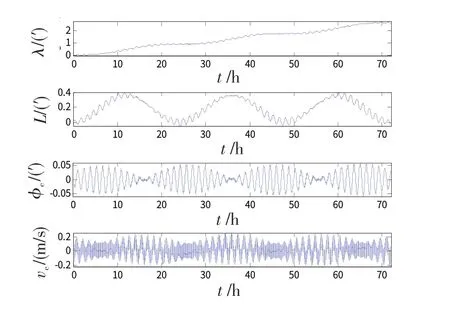
图12 载体绕z轴以1.5(°)/s(1 Hz)旋转时的惯导误差曲线Fig.12 RSINS error curves with 1.5(°)/s(1 Hz)carrier rotation on z-axis

图13 载体绕z轴以1.5(°)/s(0.01 Hz)旋转时的惯导误差曲线Fig.13 RSINS error curves with 1.5(°)/s(0.01 Hz)carrier rotation on z-axis
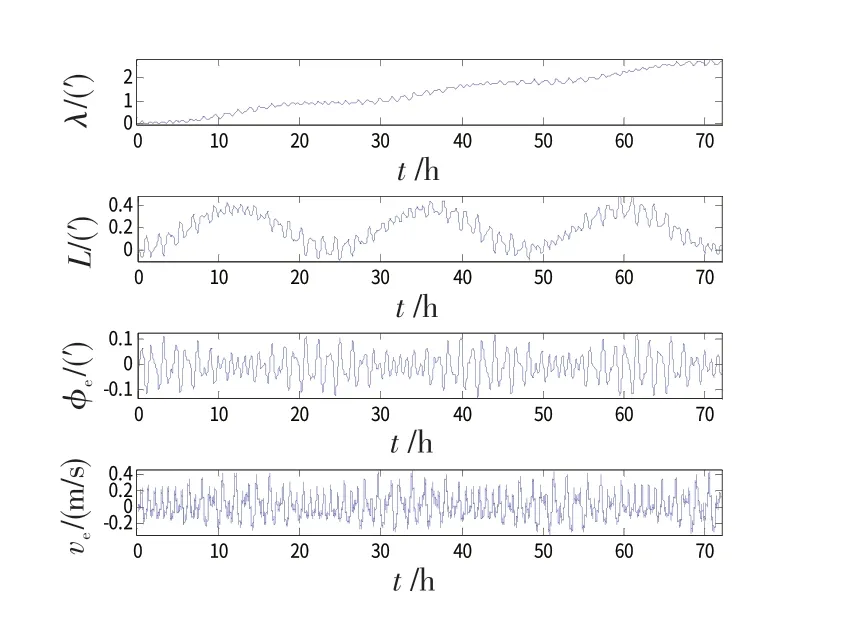
图14 载体绕z轴以4.5(°)/s(0.01 Hz)旋转时的惯导误差曲线Fig.14 RSINS error curves with 4.5(°)/s(0.01 Hz)carrier rotation on z-axis
综上所述,可以认为:正反转停方案以有限的精度代价提高了惯导系统对载体角运动的适应能力。
4 结论
国内外众多的研究表明,以光学陀螺IMU为核心的旋转捷联惯导系统具备独特的技术优点,发展和应用前景良好。然而,载体特定角运动模式对旋转调制误差补偿效果会有较大影响,且讨论进一步表明,单轴正反转停方案误差补偿效果受载体动态的影响远比连续旋转方案小。因此,在单轴旋转捷联惯导系统中采用正反转停方案虽然精度有所降低,但却大大提高了系统的环境适应能力。综合起来看,正反转停方案不失为较理想的旋转方案。
[1]袁保伦,饶谷音.光学陀螺旋转惯导系统原理探讨[J].国防科技大学学报,2006,28(6):76-80.
YUAN BAOLUN,RAO GUYIN.On the theory of optical gyro rotating inertial navigation system[J].Journal of National University of Defense Technology,2006,28(6):76-80.(in Chinese)
[2]LAHHAM J I,BRAZELL J R.Acoustic noise reduction in the MK 49 ships inertial navigation system[C]//IEEE Position Location and Navigation Symposium.1992:32-39.
[3]孙枫,孙伟,郭真.基于IMU 旋转的捷联惯导系统自补偿方法[J].仪器仪表学报,2009,30(12):2511-2517.
SUN FENG,SUN WEI,GUO ZHEN.Auto-compensation Method of SINS Based on IMU Rotation[J].Chinese Journal of Scientific Instrument,2009,30(12):2511-2517.(in Chinese)
[4]徐胜红,金斌,施建洪,等.旋转捷联惯导系统原理及典型方案分析[J].海军航空工程学院学报,2012,27(4):377-380.
XU SHENGHONG,JIN BIN,SHI JIANHONG,et al.Principle and scheme analysis of rotating strapdown inertial navigation system[J].Journal of Naval Aeronautical and Astronautical University,2012,27(4):377-380.(in Chinese)
[5]李仁,陈希军,曾庆双.旋转式捷联惯导系统误差分析[J].哈尔滨工业大学学报,2010,42(3):368-372.
LI REN,CHEN XIJUN,ZENG QINGSHUANG.Error analysis of rotating strapdown inertial system[J].Journal of Harbin Institute of Technology,2010,42(3):368-372.(in Chinese)
[6]杨益兴,田海涛,周学文.旋转式捷联惯导系统的误差分析与仿真[J].舰船电子工程,2010,30(5):86-90.
YANG YIXING,TIAN HAITAO,ZHOU XUEWEN.Error analysis and simulation of rotating SINS[J].Ship Electronic Engineering,2010,30(5):86-90.
[7]ISHIBASHI S,TSUKIOKA S,SAWA T.The rotation control system to improve the accuracy of an inertial navigation system installed in an autonomous underwater vehicle[C]//Workshop on Scientific Use of Submarine Cables and Related Technologies.2007:495-498.
[8]吴自飞,朱海,高大远,等.单轴旋转惯导系统建模与仿真[J].装备制造技术,2010(10):5-8.
WU ZIFEI,ZHU HAI,GAO DAYUAN,et al.On the modeling and simulation of single-rotating strap-down inertial navigation system[J].Equipment Manufactring Technology,2010(10):5-8.(in Chinese)
[9]ISHIBASHI S,TSUKIOKA S,YOSHIDA H.Accuracy improvement of an inertial navigation system brought about by the rotational motion[C]//OCEANS 2007 Europe.2007:1-5.
[10]李仁,曾庆双,陈希军.基于光学陀螺惯导系统的误差自动补偿技术[J].电机与控制学报,2010,14(6):98-104.
LI REN,ZENG QINGSHUANG,CHEN XIJUN.Analysis of error auto-compensation technology based on optical gyro rotating inertial navigation system[J].Electric Machines and Control,2010,14(6):98-104.(in Chinese)
[11]翁海娜,陆全聪,黄昆,等.旋转式光学陀螺捷联惯导系统的旋转方案设计[J].中国惯性技术学报,2009,17(1):8-14.
WENG HAINA,LU QUANCONG,HUANG KUN,et al.Rotation scheme design for rotary optical gyro SINS[J].Journal of Chinese Inertial Technology,2009,17(1):8-14.(in Chinese)

