Local integrable differential systems and their normal forms
Shiliang Weng, Xiang Zhang
(Department of Mathematics, Shanghai Jiao Tong University, Shanghai 200240, China)
1 Introduction
The study of the integrability of differential systems can be traced back to Newton.The theory of integrability is very useful in the dynamical analysis of differential systems,because lots of physical and mechanical systems do have invariants[1-7].How to recognize and find them is a difficult task.This paper mainly introduces some progress in recent years on local integrability.In section 2 we survey the results on the existence of local first integrals via resonance,and the equivalent characterization on local analytic integrability and the existence of analytic normalization of analytically integrable differential systems to their normal forms.In section 3 we present a new result on the existence of local first integrals for differential systems around nonhyperbolic singularities with a pair of pure imaginary eigenvalues.In section 4 we pose some open problems related to the local integrability of differential systems for further study.
2 A survey on the local integrability of analytic differential systems
This section will be separated into two parts.The first one is on the existence and the number of functionally independent local first integrals of analytic differential systems around a singularity.The second one is on the existence of analytic normalization of analytical integrable differential systems around a singularity or a periodic orbit.
2.1 Number of functionally independent local first integrals
For the analytic differential system in (n,0)

(1)
the existence of first integrals can be used to reduce the dimension of the system.And so it becomes possibly easier to study the dynamics of the system.A functionH(x) is a first integral of system(1) if
•it is continuous and is defined in a full Lebesgue measure subset Ω1of Ω,
•it is not locally constant on any positive Lebesgue measure subset of Ω1,and
•H(x) is constant along each orbit of system(1) in Ω1.
System(1) isCrcompletely integrable,if it hasn-1 functionally independentCrfirst integrals in Ω with 1≤r≤k,wherek∈∪{∞,ω}.Recall thatCr(Ω) is the set of functions whose all derivatives until orderrare continuous in Ω,and thatkfunctionsH1(x),…,Hk(x) are functionally independent in Ω if their gradients ▽H1,…,▽Hkhave rankkin a full Lebesgue measure subset of Ω.
A differentiable functionF(x) is a first integral of system(1) if
〈f(x),∂xF(x)〉≡0,x∈(n,0),
where 〈·,·〉 denotes the inner product of two vectors inn, and ∂xF=(∂x1F,…,∂xnF) is the gradient ofFand ∂xiF=∂F/∂xi.IfF(x) is a first integral of system(1) and it is
• an analytic function,thenF(x) is called an analytic first integral of system(1),
• a formal series,thenF(x) is called a formal first integral of system(1),
• a polynomial,thenF(x) is called a polynomial first integral of system(1),
• a rational function,thenF(x) is called a rational first integral of system(1),
• a meromorphic function,thenF(x) is called a meromorphic first integral of system(1),
• a ratio of two formal series,thenF(x) is called a generalized meromorphic first integral of system(1).
Denote byA=Df(0) the Jacobian matrix off(x) atx=0.Letλ=(λ1,…,λn) be then-tuple of eigenvalues ofA.We say that the eigenvaluesλsatisfy a+-resonant condition if
λ,k〉=0, for somek∈(+)n,k≠ 0,
〈λ,k〉=0, for somek∈n,k≠ 0,
Poincaré[8]studied the relation between the existence of analytic first integrals and resonance,which can be stated as the following classical result (for a proof,see for instance[9]).
PoincarétheoremIIf the eigenvaluesλofAdo not satisfy any+-resonant conditions,then system(1) has no analytic first integrals in (n,0).
In 2003 Li,Llibre and Zhang[10]extended the Poincaré′s result to the case thatλadmit one zero eigenvalue and the others are not+-resonant.
Theorem1Assume that the eigenvaluesλ=(λ1,…,λn) ofAsatisfy
The following statements hold.
(a) Forn>2, system(1) has a formal first integral in a neighborhood ofx=0 if and only if the singularityx=0 is not isolated.Specially,if the singularityx=0 is isolated, system(1) has no analytic first integrals in any neighborhood ofx=0.
(b) Forn=2,system(1) has an analytic first integral in a neighborhood ofx=0 if and only if the singularityx=0 is not isolated.
Theorem 1 was further extended to the next result (see[10,Theorem 3]).
Theorem2Assume that system(1) has 0 Then any formal first integral of system(1) is a formal series ofH1,…,Hk. This last result was extended by Zhang ([11,Theorem 1]) to the next one(see also Kwek,Li and Shi[12,TheoremA],which provided a proof of Theorem 3 with the restriction thatAis diagonalizable). Theorem3Assume that the analytic differential system(1) has 0 Here the functional independence ofH1,…,Hkis in the sense that their gradients at the origin is linearly independent. In 2008 Chen,Yi and Zhang[13]provided an upper bound on the number of functionally independent analytic first integrals for quasiperiodic differential systems.Consider the quasiperiodic vector field (2) with Ω=O(‖x‖),andf=O(‖x‖2) a vector valued analytic function periodic inθof period 2π.Denote by Xθ,xthe vector field associated to system(2),i.e. Xθ,x=ω+Ω(θ,x),∂θ〉+Ax+f(θ,x), ∂x〉. A nonconstant functionH(θ,x) is an analytic first integral(or formal first integral) of the vector field Xθ,x,ifHis an analytic function(or a formal series) and is periodic inθof period 2π,and the derivative ofHalong the vector field Xθ,xis identical zero. Letλ=(λ1,…,λn) be then-tuple of eigenvalues of the matrixA,and letγbe the rank of the set R:={(k,l)|ik,ω〉+l,λ〉=0,k∈m,l∈ Theorem4The number of functionally independent analytic first integrals of the analytic vector field (2) in a neighborhood of the constat solutionx=0 is less than or equal toγ. We note thatγis the minimal upper bound that the vector field (2) can have for functionally independent analytic first integrals.Ifγ=0,Theorem 4 is simply the Poincaré theorem I. The above results are on the existence of functionally independent analytic or formal first integrals.Shi[14]in 2007 extended the Poicaré theorem I to nonexistence of rational first integrals.He proved that if system(1) has a rational first integral,then the eigenvaluesλofAsatisfy a-resonant condition. The next result,due to Cong,Llibre and Zhang[15],extended the Shi′s result to study the existence of more than one functionally independent rational first integrals. Theorem5Assume that the differential system(1) satisfiesf(0)=0 and letλ=(λ1,…,λn) be the eigenvalues ofDf(0).Then the number of functionally independent generalized meromorphic first integrals of system(1) in (n,0) is at most the dimension of the minimal vector subspace ofncontaining the set {k∈n∶k,λ〉=0,k≠ 0}. 选取CBOE的新兴市场ETF波动率指数作为衡量原油金融属性的指标,代码VXEEM,该指标于2011年3月16日开始发布。VXEEM是采用CBOE的VIX计算方法对跟踪新兴市场ETF的期权计算出来,反映MSCI新兴市场指数基金的隐含波动率(见图9)。股市是经济的晴雨表,相较于滞后公布的许多宏观数据,股市的波动率直接反映了投资者对于未来宏观经济的信心。 Theorem 5 includes all the results mentioned above as special ones.The proof of Theorem 5 is different from the ones mentioned above.In fact the methods for proving other results cannot be adapted to the proof of Theorem 5,which contains some new ideas. SketchproofofTheorem5The proof of Theorem 5 needs the equivalent characterization of algebraic independence and functional independence.The functionsF1(x),…,Fk(x)∈(x) the field of rational functions inxare algebraically dependent if there exists a complex polynomialPofkvariables such thatP(F1(x),…,Fk(x))≡0,see for instance [16] and[17,p.152]). Lemma6The functionsF1(x),…,Fk(x)∈(x) are algebraically independent if and only if they are functionally independent. Next we need the characterization of functionally independent generalized meromorphic first integrals via their lowest order.For an analytic or a polynomial functionF(x) in (n,0),we denote byF0(x) its lowest degree homogeneous term.For a rational or a generalized rational functionF(x)=G(x)/H(x) in (n,0),we denote byF0(x) the rational functionG0(x)/H0(x).Expand the analytic functionsG(x) andH(x) as whereGi(x) andHi(x) are homogeneous polynomials of degrees degG0(x)+iand degH0(x)+irespectively,then (3) whereAi(x) andBi(x) are homogeneous polynomials.We call degAi(x)-degBi(x) the degree ofAi(x)/Bi(x),andG0(x)/H0(x) the lowest degree term ofF(x).We also denote d(G)=degG0(x),d(F)=d(G)-d(H)=degG0(x)-degH0(x), and calld(F) the lowest degree ofF. Lemma7[15]Let are functionally independent generalized rational functions,and that are functionally independent rational functions. Now we characterize rational first integrals of system(1) via their lowest order.A rational monomial is the ratio of two monomials.The rational monomialxk/xlwithk,l∈ (+)nis resonant if 〈λ,k-l〉=0.A rational function is homogeneous if its denominator and numerator are both homogeneous polynomials.A rational homogeneous function is resonant if the ratio of any two elements in the set of all its monomials in both denominator and numerator is a resonant rational monomial.Setf(x)=Ax+g(x) withg(x)=O(x2),and its associated vector field is written X=X1+Xh:=〈Ax,∂x〉+〈g(x),∂x〉. Lemma8IfF(x)=G(x)/H(x) is a generalized rational first integral of the vector field X defined by(1),thenF0(x)=G0(x)/H0(x) is a resonant rational homogeneous first integral of the linear vector field X1,where we assume,without loss of generality, thatF0is non-constant. We have enough preparation to prove Theorem 5.Let be themfunctionally independent generalized rational first integrals of X.By Lemma 7 we can assume that The study on the existence of analytic normalizations for analytic integrable vector fields to their normal forms was started from Poincaré[8]. Consider system(1),letλ=(λ1,…,λn) be then-tuple of eigenvalues of the matrixA.Set Rλ:={m=(m1,…,mn)∈ We call Rλthe resonant set ofλ,and its elements resonant lattices.Denote byrλthe number of-linearly independent vectors in Rλ.Thenrλ≤n-1 provided thatλ≠ 0. A formal or analytic differential system (4) withg(y)=O(|y|2) is a Poincaré normal form of system(1) if system(4) is in normal form,and there is a change of variables tangent to identityy=Ψ(x)=x+higher order terms transforming system(1) to (4).The transformationy=Ψ(x) is called a normalization.If the transformation contains only nonresonant terms,it is called a distinguished normalization.Correspondingly,the normal form is called a distinguished normal form.Recall that a monomialxmejin the transformation is nonresonant if 〈m,λ〉≠ 0. The Poincaré normal form theorem showed that any analytic or formal differential system(1) is formally equivalent to its Poincaré normal form.To characterize when a normalization is convergent,it is a difficult problem.One of the Poincaré classical results characterizes the planar analytic nondegenerate center via the existence of analytic normalization. PoincarétheoremⅡ[8]A planar analytic differential system(1) has the origin as a nondegenerate center if and only if it is analytically equivalent(via probably complex transformation of variables and time rescaling) to (5) whereq(u) is an analytic function inustarting from the terms of degree no less than 1. By the Poincaré theorem Ⅱ it follows that Theorem9Assume that the origin of a planar analytic differential system(1) is nondegenerate.Then the origin is an isochronous center if and only if it is analytically equivalent to withcbeing a nonzero constant. This last theorem indicates that a degenerate center of a planar analytic differential system cannot be isochronous. For planar Hamiltonian systems, Moser[18]obtained a similar result.He showed that a planar real analytic Hamiltonian system having the origin as a hyperbolic saddle can be reduced to system(5) by a real analytic area-preserving transformation of variables. Poincaré and Moser′s results on planar analytic differential systems was extended to higher dimensional differential systems by Zhang[19-20]. Theorem10Assume thatn≥ 2 andλ≠ 0,i.e.Ahas at least one eigenvalues not equal to zero.Then system(1) hasn-1 functionally independent analytic first integrals in (n,0) if and only if the-linearly independent resonant set hasrλ=n-1 elements,and system(1) is analytically equivalent to its distinguished normal form (6) by a near identity analytic normalization,whereg(y)=o(1) is an analytic function ofymwithm∈Rλand (m1,…,mn)=1. Recently this last result was extended to a neighborhood of a periodic orbit,see[21].Consider the analytic differential system (7) where Ω is an open subset ofnandf(x)∈Cω(Ω).Assume that system(7) has a periodic orbit,sayingΓ,located in the region Ω.We say that system(7) is analytically integrable in a neighborhood ofΓ,if it hasn-1 functionally independent analytic first integrals defined in the neighborhood ofΓ. Letx=φ(t) be an expression ofΓwith periodT.Thenφ(t) is analytic on.After the translationX=x-φ(t),system(7) can be written (8) withA(t) analytic and periodic intof periodT,andg(X,t) analytic inXandtand periodic intof periodT.Furthermore,it follows from the Floquet theory[22]that there is a change of coordinatesX=Q(t)YwithQ(t) invertible,analytic and periodic of periodT,which transforms system(8) into (9) whereAis a constant matrix (real or complex),andh=O(|Y|2) is analytic in its variables and periodic intof periodT.For convenience we will also use the variablexto replaceYin (9).From[22] the periodic orbit always has the characteristic multiplier 1,and soAhas always the eigenvalue 0. For the analytic functionh(x,t) periodic int,expanding it in Taylor series inxand Fourier series intwe have ik+〈l,λ〉-λj=0. System(9) is in the Poincaré-Dulac normal fom ifh(x,t) contains only resonant pseudomonomials.We note that the Poincaré-Dulac normal form defined here for periodic differential systems is an extended version of the classical one for autonomous differential systems.System(9) is formally equivalent to its Poincaré-Dulac normal form if there exists a near identity transformation x=y+Φ(y,t), (10) withΦ(y,t)=O(|y|2) a formal series inyand periodic int,which sends (9) to the Poincaré-Dulac normal form (11) IfΦ(y,t) contains only non-resonant pseudomonomials,we say that system(9) is analytically equivalent to its distinguished normal form.A pseudomonomial in a transformationxleiktejis nonresonant ifik+〈l,λ〉≠0.The transformation(10) is called distinguished normalization.We should take care of the difference between the resonances of the pseudomonomials in a vector field and in a transformation. The main results in[21] is the following one. Theorem11Assume that system(7) is analytic and has a periodic orbit.If system(7) is analytically integrable in a neighborhood of the periodic orbit, then the system is analytically equivalent to its distinguished normal form in a neighborhood of the periodic orbit. The proof of Theorem 11 explored the essential properties that the characteristic exponents of periodic orbits of analytically integrable differential system satisfy. Corollary12[21]If the analytic differential system(7) hasn-1 functionally independent analytic or formal first integrals around a periodic orbit,then the characteristic exponents of the periodic orbit satisfy λ1=υ1i,…,λn-1=υn-1i,λn=υni,υj∈. Now we present a sketch proof of Theorem 11. AsketchproofofTheorem11The proof follows from a series lemmas. The first one is on the existence of formal normal norm. Lemma13The analytic periodic differential system(9) is formally equivalent to its distinguished normal form. The second one is on first integrals under the transformation. Lemma14Assume that system(9) has an analytic or a formal first integralH(x,t) which is periodic intof periodTand that system(11) is the distinguished normal form of system(9) via the transformation(10).The following statements hold. The third one is on the nonresonant eigenvalues ofAfor analytically integrable differential system(9). Lemma15If system(9) hasn-1 functionally independent analytic or formal first integrals,then there exists anε>0 such that for allik+〈m,λ〉-λi≠0,k∈,have |ik+〈m,λ〉-λi|>ε. Using these three lemmas and the expressions of normal form systems and of the transformations,by some careful estimations we can get a proof of Theorem 11,see[21] for more details. In this section we present a new result on equivalent characterization of the existence of first integrals of system(1) near the origin with a pair of pure imaginary eigenvalues. Consider system (1),recall thatλare then-tuple of eigenvalues ofA,and that Rλis the resonant set defined in the subsection 2.2.LetL±be the invariant subspaces of the linear vector fieldAxthat correspond to the parts of the spectrum in the closed left and the closed right half planes of,respectively.ThenLc=L+∩L-is the invariant space corresponding to the part of the spectrum lying on the imaginary axis.Let Y be the Poincaré normal form of the vector field X associated to system(1).Since the Lie bracket [X1s,Y]=0,we get thatL±andLcare(formally) invariant for the(formal) vector field Y. If dimLc=2 and it is associated to a pair of pure imaginary eigenvalues,then the equation corresponding to the vector field Yc=Y|Lcand expressed in complex coordinates is of the form where ±ωiis the spectrum of X1s|Lcandgis the formal complex-valued series of one variable without free term. The exceptional set n consists of all differential systems of form(1) for which Reg=0.This definition was first given by Belitskii[23]. We have the following result. Theorem16Assume thatλcontain a pair of pure imaginary eigenvalues,saying ±i,and Rλis one dimensional in.Then system(1) has an analytic or a formal first integral around the origin if and only if system(1) belongs to n. ProofLetλ=(i,-i,λ3,…,λn).By the assumption we have that eachλjforj≥ 3 is neither pure imaginary nor zero.From the Poincaré normal form theorem system (1) is transformed into its normal form system (12) via a near identity transformationx=Φ(u,v,w)=(u,v,z)+φ(u,v,w),where we have used the conjugate complex coordinates instead of the pairs of real ones which correspond to pairs of conjugate eigenvalues,w=uv,z=(z3,…,zn)T,whereTmeans the transpose of a matrix,and whereσjforj∈{3,,…,n-1} is either 1 or 0 becauseAis in the Jordan normal form,gj(w,z) is linear inzand allziingjhave the same associated eigenvalues aszj.This last fact is from the definition of resonance. (u,v,z)=Φ-1(x)=(Ψ1(x),Ψ2(x),Ψ3(x),…,Ψn). Then Ψ1(x)Ψ2(x) is a first integral of system (1).We have completed the proof of the sufficient part and consequently the theorem. In the local theory of integrability there remains lots of unsolved open problems.We list part of them for readers′s further consideration. In Theorem 11 we obtained the existence of analytic normalization of analytic integrable differential system near a periodic orbit,but we cannot get the exact expressions. Openproblem1What is the simplest normal form of analytic integrable differential system near a periodic orbit? In all the previous results there is a basic assumption that the eigenvalues ofAare not all zero. Openproblem2If all eigenvalues ofAvanish,what kinds of analytically integrable differential systems are locally analytically equivalent to its normal form? Of course,the normal form mentioned in open problem 2 is not in the Poincaré normal form because it is trivial now.How to present a new notion and how to deform the original systems such that we can consider its Poincaré normal norm. All the above results are on a single vector field.If we have a set of linearly independent vector fields,how to study their simultaneously normal forms and the convergence of the normalization.Zung[24]studied this problem by a geometric method.His results are summarized in the following theorem. i) The vector fieldsX1=X,X2,…,Xmcommute pairwise,i.e. [Xi,Xj]=0 ∀i,j=1,…,m, and they are linearly independent almost everywhere,i.e. X1∧…∧Xm≠0. ii) The functionsf1,…,fn-mare common first integrals forX1,…,Xn-m,i.e. Xi(fj)=0, ∀i=1,…,m;j=1,…,n-m, and they are functionally independent almost everywhere,i.e. df1∧…∧dfn-m≠ 0. This theorem was proved by torus action.And it does not present an explicit expression of the normal form.Based on these facts we have the next open problem. Openproblem3Are there analytic proofs to Theorem 17? What is the exact expression of the normal form vector field ofXin Theorem 17? : [1] A. Goriely.Integrability,partial integrability,and nonintegrability for systems of ordinary differential equations[J].J.Math.Phys.,1996,37:1871-1893. [2] J. Llibre.Integrability of polynomial differential systems,Handbook of Differential Equations,Ordinary Differential Equations,Eds. A. Caada,P. Drabek and A. Fonda[M].Elsevier,2004:437-533. [3] M. J. Prelle,M. F. Singer.Elementary first integrals of differential equations[J].Trans. Amer. Math. Soc.,1983,279:215-229. [4] M. F. Singer.Liouvillian first integrals of differential equations[J].Trans. Amer. Math. Soc.,1992,333:673-688. [5] H. Yoshida.Necessary condition for the existence of algebraic first integrals.I Kowalevski′s exponents[J].Celestial Mechanics,1983,31:363-379. [6] H. Yoshida.Necessary condition for the existence of algebraic first integrals.II:condition for algebraic integrability[J].Celestial Mechanics,1983,31:381-399. [7] S. L. Ziglin.Branching of solutions and nonexistence of first integrals in Hamiltonian mechanics I[J].Functional Anal. Appl.,1983,16:181-189. [8] H. Poincaré.Sur l′intégration des équations différentielles du premier order et du premier degré Ⅰ and Ⅱ[J].Rendiconti del circolo matematico di Palermo,1891,5:161-191; 1897,11:193-239. [9] S. D. Furta.On non-integrability of general systems of differential equations[J].Z. angew Math. Phys.,1996,47:112-131. [10] W. Li,J. Llibre,X. Zhang.Local first integrals of differential systems and diffeomorphisms[J].Z. angew Math. Phys.,2003,54:235-255. [11] X. Zhang.Local first integrals for systems of differential equations[J].J. Phys. A,2003,36:12243-12253. [12] K. H. Kwek,Y. Li,S. Shi.Partial integrability for general nonlinear systems[J].Z. Angew Math. Phys.,2003,54:26-47. [13] J. Chen,Y. Yi,X. Zhang.First integrals and normal forms for germs of analytic vector fields[J].J. Differential Equations,2008,245:1167-1184. [14] S. Shi.On the nonexistence of rational first integrals for nonlinear systems and semiquasihomogeneous systems[J].J. Math. Anal. Appl.,2007,335:125-134. [15] W. Cong,J. Llibre J.,X. Zhang.Generalized rational first integrals of analytic differential systems[J].J. Differential Equations,2011,251:2770-2788. [16] A. Baider,R. C. Churchill,D. L. Rod,et al.On the infinitesimal geometry of integrable systems[R].Rhode Island:Fields Institute Communications 7,American Mathematical Society,Providence,1996. [17] W. Fulton.Algebraic Curves:An Introduction to Algebraic Geometry[M].London:The Benjamin/Cummings Publishing Com Inc,1978. [18] J. Moser.The analytic invariants of an area-preserving mapping near a hyperbolic fixed point[J].Comm. Pure Appl. Math.,1956,9:673-692. [19] X. Zhang.Analytic normalization of analytic integrable systems and the embedding Flows[J].Differential Equations,2008,244:1080-1092. [20] X. Zhang.Analytic integrable systems:Analytic normalization and embedding flows[J].Differential Equations,2013,254:3000-3022. [21] K. S. Wu,X. Zhang.Analytic normalization of analytically integrable differential systems near a periodic orbit[J].Differential Equations,2014,256:3552-3567. [22] J. Guckenheimer,P. Holmes.Nonlinear Oscillations,Dynamical Systems,and Bifurcations of Vector Fields,2nd Ed[M].New York:Springer-Verlag,2002. [23] G. R. Belitskii.Smooth equivalence of germs of vector fields with one zero or a pair of purely imaginary eigenvalues[J].Funct. Anal. Appl.,1986,20(4):253-259. [24] N. T. Zung.Convergence versus integrability in Poincaré-Dulac normal form[J].Math. Res. Lett.,2002,9:217-228.
2.2 Analytic normalization of analytical integrable differential systems
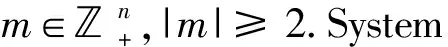
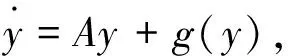
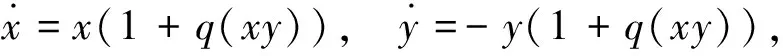
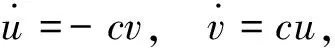
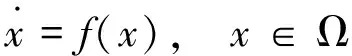


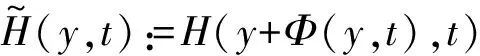

3 First integrals of differential systems near a nonhyperbolic singularity
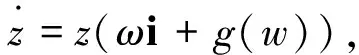


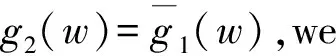
4 Open questions on local integrability



