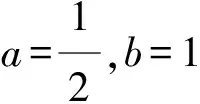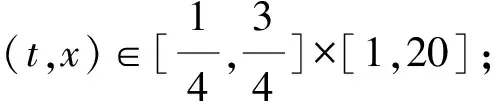Existence of positive solutions for integral boundaryvalue problem of fractional differential equations
Xiping Liu, Guiyun Wu
(College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China)
1 Introduction
Fractional differential equations have been widely applied in various modern scientific fields,such as physics,chemistry,electrodynamics of complex medium,electrical circuits and biology,etc (see [1-5]).Recently,there are many papers discussing the existence of solutions of fractional differential equations (see [6-10] and the references therein) or fractional differential equations with the fractional order linear derivative operator (see [11-13] and the references therein).
In [11],the authors used contraction mapping principle to show the existence of solutions of the following initial value problem of fractional differential equations
In [12],the existence and uniqueness for solution of the following initial problem was discussed:
whereL(D)=Dα-rtnDβ,nis a non-negative integer,r∈,0<β≤α< 1 andDα,Dβare the standard Riemann-Liouville fractional derivatives,f:+×→is a continuous function.
In this paper,we study the following integral boundary value problem
(1)
whereL(D) =Dα-rtnDβ,nis a positive integer,r∈+,0<β<1 <α< 2 withα-β≥1 andDα,Dβare the standard Riemann-Liouville fractional derivatives,fandgare given functions.
2 Preliminaries
In this section,we introduce some notations,definitions and basic lemmas about the Riemann-Liouville fractional derivative,which are used to prove our main results.
Definition1 (see [1]) The Riemann-Liouville fractional integral of orderα> 0 of a functionx:[a,b]→is given by
provided the integral exists,whereΓis the Gamma function.
Definition2 (see [1]) The Riemann-Liouville fractional derivative of orderα>0 of a functionx:[a,b]→is given by
provided the right side is pointwise defined on (0,+∞),whereN∈+andN-1<α Lemma3 (see [1]) Suppose thatx∈C[a,b] and 0<β<1,β≤α,then fractional derivativeDβx(t) is integrable and (2) Dβ(Iαx(t))=Iα-βx(t). Furthermore,if (I1-βx(t))|t=0= 0,then equation (2) will be reduced to Iα(Dβx(t))=Iα-βx(t). Lemma4 (see [2]) Letx∈C[a,b] and 0<β<1,β≤α.If (I1-βx(t))|t=0=0,then Lemma5 (see [3]) Letα> 0,then the fractional differential equationDαx(t) = 0 has solutions x(t)=c1tα-1+c2tα-2+…+cNtα-N,ci∈,i= 1,2,…,N, whereNis the smallest integer greater than or equal toα. Lemma6 (see [3]) Letα> 0, assume thatx∈C(0,1)∩L[0,1], then IαDαx(t) =x(t)+c1tα-1+… +cNtα- N,ci∈,i= 1,2,…,N, whereNis the smallest integer greater than or equal toα. (i) {x∈P(θ,b,d) |θ(x)>b}≠Ø andθ(Ax)>bforx∈P(θ,b,d); (ii) ‖Ax‖ (iii)θ(Ax)>bforx∈P(θ,b,c) with ‖Ax‖>d. Then A has at least three fixed pointsx1,x2,x3with ‖x1‖ Remark1 If there holdsd=c,then the condition of (i) of Lemma 8 implies condition (iii) of that one. We denote (H1)f:[0,1]×+→+is a continuous function. Lemma9 Suppose (H1) holds,then the boundary value problem (1) is equivalent to the following integral equation (3) where (4) (5) and (6) ProofBy Lemma 5 and Lemma 6,we obtain that IαL(D)x(t)=-Iαf(t,x(t)) and x(t)=-Iαf(t,x(t))+Iα(rtnDβx)(t)+c1tα-1+c2tα-2,c1,c2∈. (7) c2= 0. Therefore, whereG(t,s),Hk(t,s) andφ(t,s) are defined by (4),(5) and (6),respectively. Lemma10 The functionG(t,s) defined by (4) satisfies (i)G(t,s)≥0 is continuous for (t,s)∈[0,1]×[0,1], andG(t,s) > 0, for allt,s∈(0,1); (ii)G(t,s) is decreasing with respect totfor 0≤s≤t≤1 and increasing with respect totfor 0≤t≤s≤1.And (8) (iii) There exists a positive function (9) such that (10) Particularly,s0=0.5 ifα=2;s0→0.5 asα→2 ands0→0.75 asα→1. Proof(i) It is easy to show thatG(t,s) is continuous on [0,1]×[0,1] from the expression ofG(t,s). For 0≤t≤s≤1,it is obvious thatG(t,s)=(t(1-s))α-1≥0.For 0≤s≤t≤1, (t(1-s))α-1-(t-s)α-1=(t-ts)α-1-(t-s)α-1≥0. Therefore,G(t,s)≥0,for allt,s∈[0,1] ,andG(t,s) > 0,for allt,s∈(0,1). (ii) For 0≤s So,G(t,s) is decreasing with respect totfor 0≤s (iii) The proof is the same as that in [8]. Lemma11 The functionHk(t,s) defined by (6) satisfies (i)Hk(t,s) is continuous for (t,s)∈[0,1]×[0,1]; (ii)Hk(t,s)< 0 fort,s∈(0,1) and |Hk(t,s)|≤tα-1(1-s)α-β+k-1,k=0,1,2,…; Proof(i) It is obvious that (i) holds. (ii) For 0 Hk(t,s)=tn-k(t-s)α-β+k-1-tα-1(1-s)α-β+k-1,k= 0,1,…,n. Ifn-k≥1,it also means thatk≠n,thentn-k thus Hk(t,s)=tn-k(t-s)α-β+k-1-tα-1(1-s)α-β+k-1< 0. Ifk=n,we have Hn(t,s)=(t-s)α-β+n-1-tα-1(1-s)α-β+n-1< (t-s)α-β+n-1-tα-β+n-1(1-s)α-β+n-1= (t-s)α-β+n-1-(t-ts)α-β+n-1<0. Then,Hk(t,s)<0 for 0 It is obvious thatHk(t,s)=-tα-1(1-s)α-β+k-1<0 for 0 Above all,Hk(t,s)<0.For allt,s∈[0,1] andk=0,1,2,…. Hence,|Hk(t,s)|≤tα-1(1-s)α-β+k-1,k=0,1,2,…. (iii) It follows from (ii) that Since by Lemma 11 (iii),we can assume that the following condition is satisfied: LetE=C[0,1] be endowed with the norm and P={x∈E|x(t)≥0,t∈[0,1]}. ThenPis a cone on the Banach spaceE. We defineA:P→Eby (11) ProofIt is obvious that operatorAis linear. By (H2),we have |Ax(t)|≤M‖x‖,soAis bounded,that is to say the linear operatorAis bounded. It follows from (H2) that ‖Ax‖≤M‖x‖,therefore,‖A‖≤M<1,which impliesI-Ais reversible and In the following,we will give the expression of (I-A)-1. By using the theory of Fredholm integral equations,we havex(t)=(I-A)-1y(t) if and only ifx(t)=y(t)+Ax(t) fort∈[0,1]. The definition of the operatorAimplies that (12) (13) where the resolvent kernelR(t,s) is given by and whereφ1(t,s)=φ(t,s). It follows from (H2) that fort,s∈[0,1]×[0,1],we havemj≤φj(t,s)≤Mj,j=1,2,3,….Then we can obtain the following lemma. Lemma13 Suppose (H2) holds,then (14) LetT:P→C[0,1], So the solutionx(t) of boundary value problem (1) satisfiesx(t)=Tx(t)+Ax(t),that is to say x(t)=(I-A)-1Tx(t). (15) We defineS:P→C[0,1] by According to (12),(15) and Lemma 12,we know thatx(t) is the solution of (1) if and only ifx(t) is the solution ofx(t)=(I-A)-1Tx(t)=Sx(t),andx(t) is the fixed point ofS. Lemma14 If (H1) and (H2) hold,thenS:P→Pis completely continuous. ProofBy Lemma 10,(H1) and (H2),we can easily showS:P→P. SinceG(t,s) andf(t,x) are continuous,by using Ascoli-Arzela theorem,we can show getT:P→Pis completely continuous. On the other hand,(I-A)-1is linear bounded operator.It followsSis completely continuous. Denote (i)f(t,x)≤(1-M)L1r1for (t,x)∈[0,1]×[0,r1], Then the boundary value problem (1) has at least one positive solutionxsuch thatr2≤‖x‖≤r1. ProofBy Lemma 14,we knowS:P→Pis completely continuous. Let Ω1={x∈P|‖x‖ r1=‖x‖. Let Ω2={x∈P|‖x‖ r2=‖x‖. So,‖Sx‖≥‖x‖,forx∈∂Ω2. By using Lemma 7,we can get the boundary value problem (1) has at least one positive solutionxsuch thatr2≤‖x‖≤r1. (i)f(t,x)<(1-M)L1afor (t,x)∈[0,1]×[0,a]; (ii)f(t,x)>(1-m)L2bfor (t,x)∈[1/4,3/4]×[b,c]; (iii)f(t,x)≤(1-M)L1cfor (t,x)∈[0,1]×[0,c]. Then the boundary value problem (1) has at least three positive solutionsx1,x2andx3with ProofLet thenθ:P→[0,+∞) is a nonnegative continuous concave functional defined on the coneP. That is, θ(Sx)>b, for allx∈P(θ,b,c). This shows that the condition (i) of Lemma 8 is also satisfied. By Lemma 8,the boundary value problem (1) has at least three positive solutionsx1,x2andx3satisfies Example1 We consider the boundary value problem (16) By a simple calculation,we can shows0≈0.711325,L1≈2.25676,L2≈13.6649,m=0 andM=0.122. f(t,x) =tsinx+ 1≤1.8415≤(1 -M)L1r1≈1.98143,for (t,x)∈[0,1]×[0,1]. f(t,x) =tsinx+ 1≥1≥(1 -m)L2r2≈0.488031,for (t,x)∈[0,1]×[0,1/28]. Example2 Consider the boundary value problem (17) where we take that f(t,x) =14 +t+x≤35(1 -M)L1c≈39.63,for (t,x)∈[0,1]×[0,20]. By using Theorem 16,we can obtain that the boundary value problem (17) has at least three positive solutionsx1,x2andx3with : [1] I. Podlubny.Fractional differential equations [M].San Diego:Academic Press,1999. [2] K. B. Miller,B.Ross.An introduction to the fractional calculus and fractional differential equations [M].New York:Wiely,1993. [3] A. A. Kilbas,H. M. Stivastava,J. J. Trujillo.Theory and applications of fractional differential equations,in:North-Holland Mathematics Studies [J].Elsevier Science B V Amsterdam,2006,204. [4] V. Lakshmikantham,S. Leela,J. Vasundhara,et al.Theory of fractional dynamic system [M].Cambridge:Cambridge Academic Publishers,2009. [5] M. Javidi,N. Nyamoradi.Dynamic analysis of a fractional order phytoplankton model [J].J. Appl. Anal. Comput.,2013,3:343-355. [6] M. Jia,X. Liu.Multiplicity of solutions for integral boundary value problems of fractional differential equations with upper and lower solutions [J].Appl. Math. Comput.,2014,232:313-323. [7] X. Liu,F. Li,M. Jia,E. Zhi.Existence and uniqueness of the solutions for fractional differential equations with nonlinear boundary conditions [J].Abstr. Appl. Anal.,2014,Article ID 758390,11,pp.1-11. [8] Z. Bai,H. Lu.Positive solutions for boundary value problem of nonlinear fractional differential equation [J].J. Math. Anal. Appl.,2005,311:495-505. [9] X. Liu,L. Lin,H. Fang.Existence of positive solutions for nonlocal boundary value problem of fractional differential equation [J].Cent. Eur. J. Phys.,2013,11:1423-1432. [10] M. Jia,X. Liu.The existence of positive solutions for fractional differential equations with integral and disturbance parameter in boundary conditions [J].Abstr. Appl. Anal.,2014,Article ID 131548,14,pp.1-14. [11] D. Baleanu,O. G. Mustafa.On the global existence of solutions to a class of fractional differential equations [J].Math. Comput. Appl.,2010,59:1835-1841. [12] A. Babakhani.Existence and uniqueness of solution for class of fractional order differential equations on an unbounded domain [J].Adv. Difference Equ.,2012,41:1-8. [13] J. R. Graef,L. Kong,Q. Kong,M. Wang.Uniqueness and parameter dependence of positive solutions to higher order boundary value problems with fractional q-derivatives [J].J. Appl. Anal. Comput.,2013,3:21-35. [14] M. A. Krasnosel′skii.Positive solutions of operator equations [M].Noordhoff.Groningen.1964. [15] R. W. Leggett,L. R. Williams.Multiple positive fixed points of nonlinear operators on ordered Banach spaces [J].J.Math Indiana Univ,1979,28:673-688.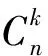
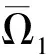
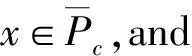
3 Expression and Properties of Integral Kernel

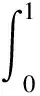
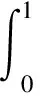
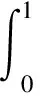
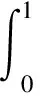
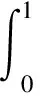
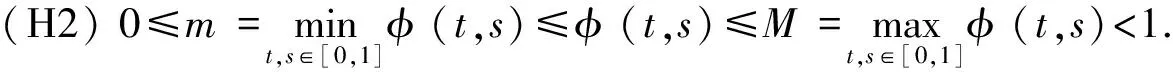
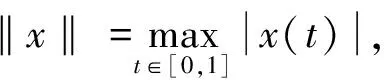

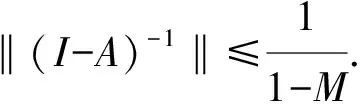



4 Main results


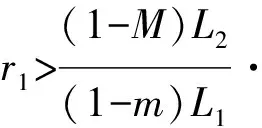






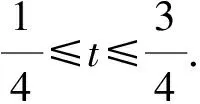

5 Illustrations