Exact parametric representations of orbits defined by cubic Hamiltonian
Jibin Li
(Department of Mathematics, Zhejiang Normal University Jinhua, Zhejiang 321004, China)
1 Introduction
We are interested in the study of planar vector fields because they occur very often in applications.Indeed,such equations appear in modelling chemical reactions,population dynamics,travelling wave systems of nonlinear evolution equations in mathematical physics and in many other areas of applied mathematics and mechanics.
It is known that a planar quadratic Hamiltonian vector field
(1)
defines a family of cubic algebraic curves:
F(x,y)=Ax3+3Bx2y+3Cxy2+Dy3+3Ex2+6Fxy+3Gy2+Hx+Iy-h=0.
(2)
For every given real numberh,the curves defined byF(x,y)=0 are called the level curves or the orbits of system (1).
Can we have the exact explicit parametric representationx=x(t),y=y(t) for a given cubic curve? This is an interesting problem.In fact,for a given nonlinear wave equation,if its corresponding traveling wave system is a planar quadratic integrable system,to obtain exact traveling wave solutions,we need to solve the above problem.
In this paper,we show that for any given planar cubic algebraic curves,we can always have their exact explicit parametric representations.To obtain this conclusion,we first introduce the classification of cubic curves given by Newton and a method that makes a general cubic curves become corresponding classification types.Second,for the (A)-type curves,we show that it is easy to get the exact explicit parametric representations.In section 3,we use the normal form given by Horozov & Iliev[1]to prove that any cubic curves defined by a quadratic Hamiltonian system can get their exact explicit parametric representations.As an example,we discuss the traveling wave solutions for a model of micro-structured solid.We give the formulas,for which we can obtain the exact explicit parametric representations of the traveling wave solutions.
2 Preliminary:cubic algebraic curves
In 1704,Newton classified the cubic algebraic curves of the form(2) into the following four types[2-3]:
Question1How to make form(2) become one of the above four types?
We write thatf3(x,y)=Ax3+3Bx2y+3Cxy2+Dy3,f2(x,y)=3Ex2+6Fxy+3Gy2,f1(x,y)=Hx+Iy.
1.Suppose thatf3(x,y)=(α1x+β1y)(α2x+β2y)(α3x+β3y) withαkβj-αjβk≠0(j≠k),whereα1andβ1are real numbers.In this case,letu=α1x+β1y,v=x, thenf3(x,y) becomes

(3)

2.Suppose thatf3(x,y)=(α1x+β1y)2(α2x+β2y), whereα1β2-α2β1≠0 andαi,βjare real.Letξ=α2x+β2y,η=α1x+β1y, form (2) becomes
(4)

3. Suppose thatf3(x,y)=(α1x+β1y)3. In this case,letξ=α1x+β1y,η=y, (ifα1=0,letξ=β1y,η=x), now form(2) becomes
(5)
We consider the following four cases.
u3+b20u2+b10u+b02v2+b01v+a00=0.
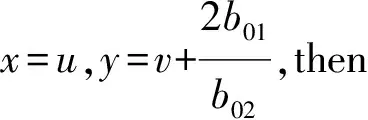
Clearly,we see from the forms(B),(C) and (D) that it is very easy to expressyas the functions ofx.We next only consider the form(A).
Question2How to get the parametric representations of all level curves given by (A)-type curves.
Let
H(x,y)=xy2+ey-(ax3+bx2+cx)=h
(6)
be a family of the cubic curves of (A)-type,which is the family of integral curves of the following quadratic Hamiltonian vector field:
(7)
By (6) and (7),we know that
Thus,we have
(8)
By calculating the elliptic integral (8),we can obtain the parametric representations of all level curves defined by (6).
3 Exact parametric representations of orbits defined by cubic Hamiltonian
In [1],the authors stated that any cubic Hamiltonian,with at least one period annulus contained in its level curves,can be transformed into the following normal form,
(9)
wherea,bare parameters lying in the region
and moreover,their respective vector fieldsXHdefined by
(10)
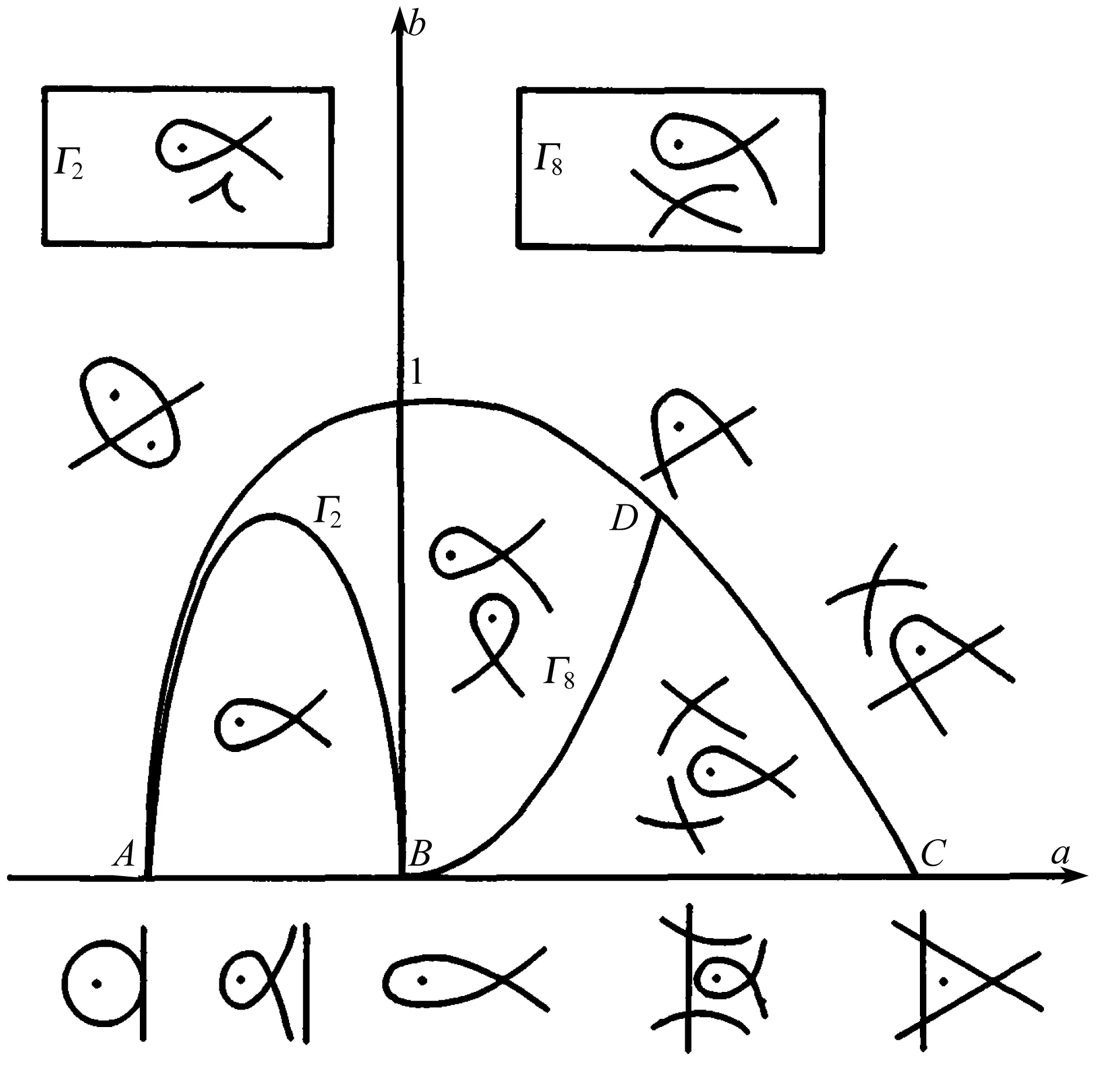
Fig.1 Bifurcation diagram in the (a,b)-plane of the level curves defined by H(x,y)=h
In order to find the parametric representations of orbits of system(10),we need to make cubic Hamiltonian(9) become the cubic curves of the type(A) in section 2.Notice that for (9),we have
Use the results in section 2.Make the transformation series:
i.e.,
(11)

(12)
Clearly,corresponding to(8),now the functionG(x,h) changes to
(13)
Thus, using the result in section 2,we have the following conclusion.
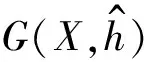
4 An example of application:exact travelling wave solutions for the model of microstructured solids
Microstructured materials like alloys,crystallites,ceramics,functionally graded materials,etc.,have gained wide applications.There are a lot of modelling of wave propagation in such materials[4-6].In[7],the author presented a mathematical model for longitudinal waves in the 1D setting which describes nonlinear wave motion in micro-structured solids.The governing system is the following:
ρ0utt=auxx+Nuxuxx+AΨx,IΨtt=CΨxx+MΨxΨxx-Aux-BΨ,
(14)
whereudenotes the longitudinal(macro)displacement andΨis the micro-deformation (according to the Mindlin mode) or the internal variable (according to the concept of internal variables).Further,ρ0is the density andIinertia of the micro-structure,while,a,A,B,C,N,Mare the material parameters specifying the free energy function.After introducing the dimensionless variablesU,X,Tand applying the “slaving principle”,system(14) is reduced to one equation[8]:
(15)
wherec0,c1,cA,cBare velocities andkN,kMare the parameters expressing the strengths of physical nonlinearities on macro-and microscale,respectively.
In [8],the authors considered the existence of solitary wave solutions of (15).We notice that the dynamical behavior of the travelling wave solutions of (15) have not been discussed before.
We look for travelling wave solutions to (15) of the formU(X,T)=U(X-cT)=U(ξ), wherecis the wave speed andξ=X-cT.Substituting the above travelling wave solutions into (15),lettingU′(ξ)=φ(ξ), and integrating it with respect toξonce,we obtain
(16)
where we take the integral constant as zero.
withαβγ≠ 0. Thus,equation (16) is equivalent to the planar system
(17)
with the first integral
(18)
Because system (17) is a travelling system with respect to the variableU′(ξ)=φ(ξ),we call it an associated travelling wave system of (15) in order to differ the travelling wave system with respect to the variableU.
Clearly,if we know an exact solutionφ(ξ) of (17),then, a solution of equation (15) has the form

(19)
We now consider the associated regular system of (17)
(20)
where dξ=(α+βy)dζ. This system is a quadratic Hamiltonian system with the Hamiltonian as (18).
By the conclusions in section 3,we make the transformation
(21)
with the inverse transformation:
(22)
Under these transformations,system (17) and Hamiltonian (18) become
(23)
and
(24)
In order to obtain the exact explicit parametric representations of the solutions of (17) and (20),we solveH1(Φ,Y)=hto obtain that
(25)
where
(26)
and
By using (25),we have
(27)
From the first equation of(23),we obtain

(28)
Therefore,we can use (28) to get the exact explicit parametric representations ofΦ(ζ) of the solutions of (23).
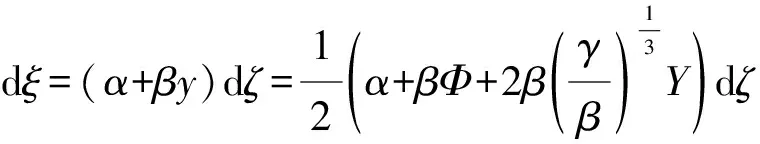
(29)
(30)
Thus,we obtain the following conclusion(for details,see[9]).
Theorem2By using the transformation formula (22) and the formulas (28)-(30), the exact explicit parametric representations of the solutions of system(17) can be given.
:
[1] E. Horozov,D. Iliev.On the number of limit cycles in perturbations of quadratic Hamiltonian systems[J].Proc. London Math. Soc.,1994,69(3):198-224.
[2] S. B. Mulay.Classification of plane cubic curves,Advances in commutative ring theory(fez,1997),461-482,Lecture Notice in Pure and Appl. Math.,Dekker,New York,1999,205.
[3] A. S. Smogorzhevskii,E. S. Stolova,Handbook on the theory of planar curves of the third order[M].Moscow:Fizmatgiz,1961.
[4] A. C. Eringgen.Microcontinuum Field Theories.I Foundations and Solids[M].New York:Springer,1999.
[5] R. Phillips.Crystal,Defects and Microstructures.Modelling Across Scales,Cambridge University Press,Combridge,2001.
[6] S. Suresh,A. Mortensen.Fundamentals of Functionally Graded Materials[M].London:IOM Comm. Ltd.
[7] J. Engelbrecht.Nonlinear wave motion and complexity[J].Proceedings of the Estonian Academy of Sciences,2010,59(2):66-71.
[8] J. Janno,J. Engelbrecht.Solitary waves in nonlinear microstructured materials[J].J. Phys. A.:Math Gen,2005,38:5159-5172.
[9] J. B. Li,G. R. Chen.Exact travelling wave solutions and their bifurcations for the model of microstructured solids[J].Int. J. Bifurcation and Chaos,2013,23(1),1350009.
- 上海师范大学学报·自然科学版的其它文章
- Analysis of a multi-patch dynamical model about cattle brucellosis
- The dynamics of poverty and crime
- Global bifurcation of a cubic system perturbed by degree four
- Local integrable differential systems and their normal forms
- Existence of positive solutions for integral boundaryvalue problem of fractional differential equations
- The Cayley graph built upon the semigroup ofleft ideals of a ring

