The Cayley graph built upon the semigroup ofleft ideals of a ring

Aihua Li, Ralph P.Tucci

(1.Department of Mathematical Sciences, Montclair State University, Montclair, New Jersey 07043, USA;2.Department of Mathematical Sciences, Loyola University New Orleans, New Orleans, Louisiana 70118, USA)

1 Introduction

A directed graph or digraphGis a pair of sets,the setVof vertices and the setEof edges,denotedG=(V,E), whereV≠Ø andE⊆V×V.Ifv,w∈Vand (v,w)∈E,then (v,w) is denoted byv→w.The edgev→wis said to be incident fromvand incident tow.An edge fromvto itself is a loop.We allow multiple edges between two vertices ofG.Directed graphs with loops and multiple edges are often referred to as quivers.A subdigraph ofGis a digraphG′=(V′,E′),whereV′⊆VandE′⊆E.

A path of lengthninGfrom vertexvto vertexwis a sequence of edgesv→v1→v2… →vn=wwhere the vertices are all distinct.The distance fromvtowis the length of the shortest path fromvtow.The eccentricity of a vertexvis the maximum of its finite distances to all other vertices.The radius ofGis the minimum eccentricity of all its vertices.The diameter ofGis the maximum eccentricity of all its vertices; i.e.,the diameter is the maximum distance between all pairs of distinct vertices inG.

A digraphGis strongly connected if there is a path from any vertex to any other vertex.A maximal strongly connected subdigraph ofGis a strongly connected component ofG.

A cycle from vertexvto itself inGis a path fromvto some vertexwtogether with an edge fromwtov.The girth ofGis the length of the smallest cycle inG.The circumference ofGis the length of the largest cycle inG.

IfG=(V,E) is a directed graph,then the underlying graph ofGis the undirected graphG′= (V′,E′ ),whereV′=VandE′={{v,w}|(v,w)∈E}.That is,G′ is constructed by takingGand "removing the directions" on the edges.As before,V′ is the set of vertices ofG′,andE′ is the set of edges ofG′.The edge {v,w} is denotedv-w.A digraphGis called weakly connected if its underlying graph is a connected graph.

Given a Cayley graph,we can define the underlying non-directed graph as above by replacing multiple edges by a single edge and removing the directions on the edges.We also remove the labels on the edges.We do not eliminate loops.

Figure 1 Cay((2[[x]]/(x3)),*(2[[x]]/(x3)))

As an example of a Cayley graph,letR=2[[x]]/(x3).The left ideals ofRaregraph Cay((R),*(R)) is given in Figure 1.

2 Basic Graph-Theoretic Properties

Definition1LetGbe a digraph.The transitive closure ofGis the graph obtained by adding an edgev→wwhenever there is a path fromvtow.If a digraphGis equal to its transitive closure,thenGis said to be transitively closed.

ProofLetH,Kbe any two left ideals ofR.Suppose that there is a path fromHtoKof the form

Example3The Calyley graph needs not be connected.LetR=2×2.LetH=2×0 and letK=0×2.There is no path fromHtoKor fromKtoH.

1.Ifn≥2,then in the underlying graph the corresponding undirected path is in a cycle of lengthn+1.

2.Letn≥3.Fix an edgeein the path fromHtoK.Then there is a path fromHtoKof length 3 which includes the edgee.

3 Stars and Completeness

Definition7A directed graphGwithout cycles is an inward star if there is a vertexvsuch that every vertex is adjacent tovand every edge is labeled byv.In this case we say thatvis the center ofG.

Definition8LetGbe a directed graph.A subdigraphG′ ofGis a spanning subdigraph ofGifG′ contains all the vertices ofG.

Definition9A ringRis subdirectly irreducible if the intersectionAof all the non-zero two-sided ideals ofRis non-zero.The idealAis the heart ofR.

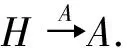
We can apply this result to simple rings.The next result is from [1,Prop.4.3].

Lemma11A ringRis simple if and only ifHK=Kfor any non-zero left idealsH,K.

ProofLetRbe simple and letH,Kbe non-zero left ideals ofR.ThenHK=H(RK)=(HR)K=RK=K.Conversely,ifHK=Kfor any non-zero left idealsH,KofR,then letH=Rafor any 0≠a∈R,and letK=R.ThenRaR=Rfor any 0≠a∈R,and henceRis simple.

Definition12A directed graph is complete if between any two vertices there is an edge in each direction.

Example15LetF=2.The left ideals are 0,R,H1,H2,H3,where

Note that ifH,Kare nonzero left ideals,thenHK=Kand the corresponding edge in Cay(*(R),*(R)) is

4 Cycles and Loops

Letfbe any other idempotent inR.Thenef-fe=1·(ef-fe)=(f+1-f) (ef-fe).Nowf(ef-fe)=fef-fe=fef-fef=0.Also,(1-f)(ef-fe)= (1-f)(ef-fe)(1-f).A straightforward computation shows that this expression is 0.Thereforeef=fefor any two idempotents.It is known that,in any ring,if all the idempotents commute with each other,then the idempotents are central.

Definition17A semigroupSwith 0 is right cancellative ifxs=ys≠0 impliesx=yfor all 0≠s,x,y∈S.

IfHis a left ideal ofR,thenHR=HR2.By right cancellation,we haveH=HR.HenceRis left duo.In particular,ifeis an idempotent ofR,thenRe=ReR.The result now follows from the proof of Proposition 16.

Note that the power series ring in one indeterminate over a field satisfies the hypothesis of Proposition 16.Commutativity of the idempotents under the hypotheses of Proposition 16 also follows from [2,Prop.2.8 and Prop.4.1].

Definition19A ringRis left weakly regular (l.w.r.) ifH2=Hfor any left idealHofR.Right weakly regular rings are defined dually.

For a survey on right weakly regular rings,see [4].

Lemma20[2,Prop.3.1(a)] IfMis a maximal left ideal ofR,then eitherM2=MorMis a two-sided ideal.

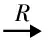
The converse of Proposition 21 is false.LetRbe a simple ring.ThenRis (l.w.r.) by Lemma 11,butHR=Rfor avery nonzero left idealHofR.

Corollary22LetRsatisfy the conditions of Proposition 21.LetJ(R) denote the Jacobson radical ofR.ThenR/J(R) is a subdirect product of simple rings.

Suppose that the idealsH,Kare in the same cycle.By Prop.2 there exist idealsX,Ysuch thatHX=KandKX=H.But thenH⊇KandK⊇H,so thatH=K.

:

[1] H.E.Heatherly,R.P.Tucci.The Semigroup of Right Ideals of a Ring [J].Math.Pannonica,2007,18/1:19-26.

[2] H.E.Heatherly,R.P.Tucci.Rings Whose Semigroup of Right Ideals is J-Trivial [J].The Intrenational Electronic Journal of Algebra,2011,10:151-161.

[3] G.F.Birkenmeier.Idempotents and Completely Semiprime Ideals [J].Comm.Algebra,1983,11:567-580.

[5] H.P.Yu.On Quasi-Duo Rings [J].Glasgow Math.J.,1995,37:21-31.