Global bifurcation of a cubic system perturbed by degree four
Desheng Shang, Zheng Wang
(Department of Mathematics, School of Sciences,Shandong University of Technology, Zibo 255049, China)
1 Introduction
Hilbert sixteenth problem has been extensively studied in the last few decades, especially for quadratic and cubic systems[1-19]. However there are many works (see for instance [4,6,9,10,11,16] etc.) discussing on the study of the following system
(1)

In this paper, we study the following system
(2)
wheref3(x,y) =a1+a2x+a3x2+a4x3+a5y2+a6xy2.
Remark1 This is a case of system (1) whenf(x,y)=yf3(x,y),b∈R.
Remark2 Of the three cases, i.e.b>0,b=0, andb<0, only the case ofb>0 is studied in detail in this paper, for the case ofb<0 can be transformed tob>0 throughb→-b, and whenb=0, the analysis is similar and results are simple than the case ofb>0.
Our main result is stated in the following theorem.
Theorem1 The system (2) can have nine limit cycles, with their distributions being 3+(3, 3) and 2+(3, 4) (see Fig 3).
2 Studying on perturbed homoclinic loops and main lemmas
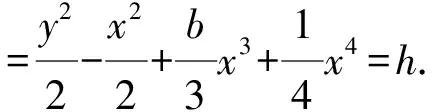
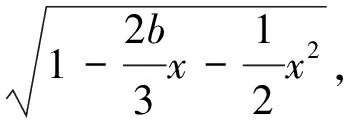


Mi(a) =-∮Li(a1+a2x+a3x2+a4x3+a5y2+a6xy2)ydx=
2[Ai1a1+Ai2a2+Ai3a3+Ai4a4+Ai5a5+Ai6a6],
(3)
andgiare fixed positive numbers fori=1,2, and whereAij,i=1,2,j=1,2,…, 6 in (3) are given as follows,
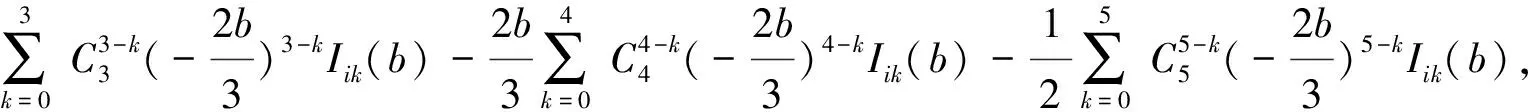

and
I2j(b)=(-1)j-1I1j(-b),A2j(b)=(-1)j-1A1j(-b) ,j=1, 2, 3, 4.
We easily obtain
Lemma1 (i) Assume thatb>0. Then there exists a function

(4)
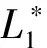
(ii) Ifa2=K2(ε,a1,a3,a4,a5,a6) holds, then there exists a function
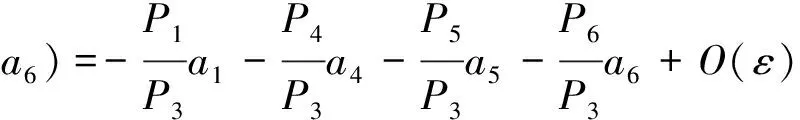
(5)




Proof(i) follows directly from the expression ofM1(ε,a) in (3), and substitutinga2=K2(ε,a1,a3,a4,a5,a6) into the expression ofM2(ε,a) in (3), we get
Therefore, we getd2≥0(<0) if and only if
according toP3<0. Thus the proof (ii) of the Lemma is completed.
We easily get the divergence of the system (2) at the origin is div(2)|Oε(0, 0)= -εa1+O(ε2), therefore the following lemma holds.
Lemma2 There exists a function
K1(ε,a4,a5,a6)=O(ε) ,
(6)
such that div(2)|Oε(0, 0)≥0(<0) if and only ifa1≤(>)K1(ε,a4,a5,a6).
By [2-3], we have the following result.
Lemma3 Whenai=Ki,i=1,2,3 hold, the integral
δi0= ∮Li*(a1+a2x+a3x2+a4x3+3a5y2+3a6xy2)dt
is converging at both sides ast→±∞ , and
δi0= ∮Li(a1+a2x+a3x2+a4x3+3a5y2+3a6xy2)dt+O(ε) ,i=1, 2.
(7)
Now, we will compute (7) under conditionsai=Ki,i=1,2,3. Direct calculation shows
a1+a2x+a3x2+a4x3+3a5y2+3a6xy2=

whereTij=∮Lixjdt,i=1,2,j=1,2,…, 5,Dij=∮Lixj-1y2dt,i,j=1, 2 andT2j(b)=(-1)jT1j(-b).
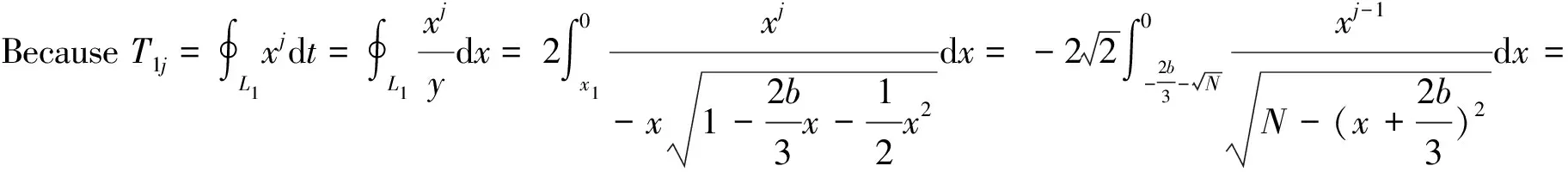
By direct computation, we have





Therefore, for allb≥0, we have
δ10(b)= [g(b)/(20b6+90b4+81)]a4+
Thus the implicit function theorem implies that the following lemma holds.
Lemma4 Under conditionsai=Ki,i=1,2,3, there exists a functionK4(a5,a6,ε) such that
δ10(b)≥0 if and only ifa4≥K4(a5,a6,ε) forb∈(0,b1)∪(b2, +∞) ,
anda4≤K4(a5,a6,ε) forb∈(b1,b2),
(8)
whereK4(a5,a6,ε)=p1a5+p2a6+O(ε), and
Under conditionsai=Ki,i=1,2,3,4, by direct computation, we have
Settingδ20(b)=0 and using the implicit function theorem, we have
Lemma5 Under conditionsai=Ki,i=1,2,3,4, there exists a function
(9)
such thatδ20(b)≥0 if and only ifa5≥K5(a6,ε) .
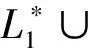
[fxy(fyy-fxx) +gxy(gyy-gxx)-fxxgxx+fyygyy]/λ},
whereλ>0 and the right-hand side function is evaluated at the origin (see [7]).
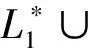
wherer(b)=243-1620b2-3348b4-768b6-128b8.
Using Mathematica 5.0, we easily give the figure ofr(b) in Figure 1(2) and obtain that it has a unique rootb(2)=0.34584269841197390867. ThereforeR11>0 when 0
According to [5] and [7], we have the following lemma.
Lemma7 If the homoclinic loopLiis along the clockwise direction, and the first saddle valueR11>0 (resp. <0), thenLiis stable (resp. unstable) inside; if the double homoclinic loopL=L1∪L2is along the clockwise direction, and the first saddle valueR11>0 (resp. <0), then the double homoclinic loopLis unstable (resp. stable) outside.
3 Research on the foci′s stability and the boundedness of system (2)

-ε{ [a2-ba3+a4(1+b2)]xi0+(a3-ba4)}+O(ε2) =
wherefi(b)=xi0(324b+135b3+1716b5+460b7) + (243-2403b2-3816b4-972b6).
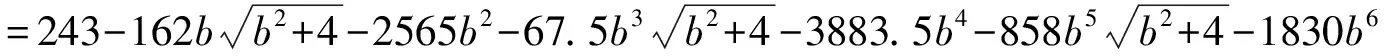


Figure 1 The figure of the functions g(b),r(b) and f2(b).Here (1) is the figure of g(b),(2) is the figure of r(b), and (3) is the figure of f2(b)

H(B)-H(A)=-ε∮Γ h(a1+a2x+a3x2+a4x3+a5y2+a6xy2)ydx+O(ε2) .
Under conditionsai=Ki,i=1,2,…,5, and noting that
we thus have
H(B)-H(A) =-εa6[E1∮Γhx2y2dy+E2∮Γhxy2dy+E3∮Γhx4dy
+E4∮Γhx3dy+E5∮Γhx2dy]+O(ε2) ,
(10)
where


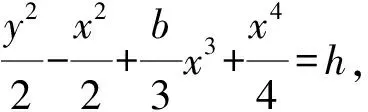
(11)

Therefore we have
(12)
Thus under this transformation, we have the closed curveΓhchanges intoγh:u4+y2=2h,h>0 for sufficiently largeh, and the directions of them are both clockwise.
A simple computation gives the following results hold
Lemma8 Along the closed curveγh:u4+y2=2h,h>0, we have
The proof of Lemma 8 is simple using the fact that
Then along the closed curveΓhin (10), we get that the integrals ∮Γhxiyjdyhave the following asymptotic expressions for sufficiently largeh.

Substituting these asymptotic expressions in (10) we get
(13)
Thus forhsufficiently large, the sign ofH(B)-H(A) is determined by the sign of the highest term ofh, therefore determined by the sign ofW(b). Thus we obtain that ifb∈(0,b*), thenW(b)>0, this impliesH(B)
By the analysis stated above, we get table 1 (whereb≠b1andb≠b2forb>b(3), and denoteci=div(2)Piε,i=1,2).

Table 1 The values which determining qualitative analysis of system (2)
4 The analysis and proof of the main result
Now, we will finish the proof of the main result. For convenience, we give the assumptions thata6>0 andε>0 is small enough.
According to table 1, we can divide our analysis into five cases.By the previous analysis, we have that all the trajectories are bounded outside the double homoclinic loopL*in case (I) and (II) of table 1, and unbounded outside the double homoclinic loopL*in case (III), (IV) and (V).
Case(I) Whenb∈(0,b(1)), we haveR11>0, andci>0,i=1,2 according to table 1.

Figure 2 The limit cycle distributions of system (2) in case (I)


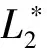
Thus,in general,according to above arguments,we have that system (2) can exist at least 8 limit cycles in the case I,their distributions are shown in Figure 2,we denote as 3+(3, 2) and 2+(3, 3), respectively.
Case(II) Whenb∈(b(1),b*), we haveR11>0, andc1<0,c2>0 according to table 1.
The following analysis are the same as case (I). And finally, we get the system (2) can have 9 limit cycles in this case, their distribution are 3+(3, 3) and 2+(3, 4), see Figure 3.

Figure 3 The limit cycle distributions of system (2) in case (II)
For the analysis of Case (III), Case (IV) and Case (V), similar to the analysis of case (I) and case (II) (omitted for brief), we obtain that the system (2) have 8 limit cycles with distributions 2+(4, 2) and 1+(4, 3) in case (III); 9 limit cycles with distributions 3+(3, 3) and 2+(3, 4) in case (IV); and 8 limit cycles with distributions 2+(3, 3) and 3+(2, 3) in case (V), respectively.
:
[1] Z. Cheng,J. Ren.Periodic solution for high-order differential system[J].Journal of Applied Analysis and Computation, 2013,3(3):239-249.
[2] M. Han.Cyclicity of planar homoclinic loops and quadratic integrable systems[J].Sci. China,1997,40A(12):1247-1258.
[3] M. Han,J. Chen.On the number of limit cycles in double homoclinic bifurcations[J].Sci. China,2000,43A(9):914-928.
[4] M. Han.On the number and distributions of limit cycles in a cubic system[J].Chinese Annals of Mathematics,2002,23A(2):143-152(In Chinese).
[5] M. Han,S. Hu,X. Liu.On the stability of double homoclinic and heteroclinic cycles[J].Nonlinear Analysis,2003,53:701-713.
[6] M. Han,C. Fan.On the number and distributions of limit cycles in a quartic system[J].Chinese Annals of Mathematics,2005,26A(6):825-834.
[7] M. Han,T. Zhang.Some bifurcation methods of finding limit cycles[J].Mathematical Biosciences and Engineering,2006,3(1):67-77.
[8] M. Han.Remarks on the center and focus problem for planar systems[J].Journal of Shanghai Normal University(Natural Sciences),2013,42(6):565-579.
[9] E. Horozov,I. D. Ilieve.Linear estimate for the number of zeros of Abelian integrals with cubic Hamiltonian[J].Nonlinearity,1998,11:1521-1537.
[10] I. D. Ilieve,High-orger Melnikov functions for degenerate cubic Hamiltonians[J].Adv. Diff. Equs.,1996,1(4):689-708.
[11] I. D. Ilieve,I. M. Perko.Higher order bifurcations of limit cycles[J].J. Diff. Eqns.,1999,154:339-363.
[12] C. Li,C. Liu,J. Yang.A cubic system with thirteen limit cycles[J].J. Differential Equations,2009,246:3609-3619.
[13] J. Li.Hilbert′s 16th problem and bifurcations of planar polynomial vector fields[J].Int. J. Bifurcation and Chaos,2003,13(1):47-106.
[14] N.G. Lloyd,J. M. Pearson.A cubic differential system with nine limit cycles[J].Journal of Applied Analysis and Computation,2012,2(3):293-304.
[15] Rasool Kazemi,Hamid R. Z.Zangeneh.Bifurcation of limit cycles in small perturbations of a hyper-elliptic Hamiltonian system with two nilpotent saddles[J].Journal of Applied Analysis and Computation,2012,2(4):395-413.
[16] D. Shang,M. Han,J. Sun.The global bifurcation of a cubic system,Acta Mathematicae Applicatae Sinica[J].English Series,2006,22(2):325-332.
[17] X. Wei,S. Shui.The shape of limit cycles for a class of quintic polynomial differential systems[J].Journal of Applied Analysis and Computation,2012,3(3):291-300.
[18] J. Yang,M. Han,J. Li,et al.Existence conditions of thirteen limit cycles in a cubic system[J].Int. J. Bifurcation and Chaos,2010,20(8):2569-2577.
[19] J. Yang.On the limit cycles of a kind of Liénard system with a nilpotent center under perturbations[J].Journal of Applied Analysis and Computation,2012,2(3):325-339.
- 上海师范大学学报·自然科学版的其它文章
- Analysis of a multi-patch dynamical model about cattle brucellosis
- The dynamics of poverty and crime
- Exact parametric representations of orbits defined by cubic Hamiltonian
- Local integrable differential systems and their normal forms
- Existence of positive solutions for integral boundaryvalue problem of fractional differential equations
- The Cayley graph built upon the semigroup ofleft ideals of a ring

