The dynamics of poverty and crime
Haiyun Zhao, Zhilan Feng, Carlos Castillo-Chavez
(1.Law School, Yale University, New Haven, CT 06511, USA;2.Department of Mathematics, Purdue University, West Lafayette, IN 47907, USA;3.Mathematical and Computational Modeling Sciences Center,Arizona State University, Tempe, AZ 85287, USA)
1 Introduction
There is a direct correlation between the poverty and criminality[2-3].Becker′s economic theory of crime[1]assumes that people resort to crime only if the costs of committing the crime are lower than the benefits gained.Those living in poverty,therefore,have a much greater chance of committing property crime[3-4]than the general population,as they stand to gain more with each crime.Property crime includes the offenses of burglary,larceny-theft,motor vehicle theft,and arson[5].In his 1968 paper[1],Becker used statistical and economic analysis to determine the optimal control of crime.Here,we use a system of ordinary differential equations (ODEs) to try and get a more realistic,dynamical solution to that same question.


One of the main objectives of this modeling study is to find a cost-effective strategy to lower criminality,thus lowering the cost of crime to society.Pervious works have addressed this problem[1,13]using statistical and economic approaches,while we do so by taking a mathematical approach.The use of ODEs allows us to examine the interactions between poverty,crime and intervention,which provides a dynamic,rather than static,view of how criminality is affected by varying intervention parameters.
It is known that the problem of crime is alleviated by either decreasing poverty[14]or by increasing the severity of the ensuing punishment[15].Our model considers both intervention measures concomitantly.Logically,crime will decrease if one or the other intervention parameters is increased.However,because we seek a pragmatic solution in a world where resources are limited and cost is always a consideration,we cannot reduce crime by simply relieving all poverty or by incarcerating all criminals.Instead,we seek a cost-effective strategy to combat crime.Our model shows that the optimal solution is actually a combination of the two control measures and pinpoints where that optimal solution is.
2 Model
Naturally,not all crime can be stopped;that would not be economically desirable.This model seeks to optimize interventions so that crime is reasonably controlled while the cost is minimal,or crime level is minimal under a given constraint on cost.The two intervention measures considered in the model are represented byγ,the rate of converting those in poverty to recovered,andρ,the rate of incarceration,which can vary due to the change in the effort of enforcement.In the model,the population is divided into five sub-classes:the non-impoverished classN,the poverty classP,the criminal classC,the jailed classJ,and recovered class (from jail or from impoverished class)R.Let these variables represent the fractions of the sub-popuations at timet.Then
N(t)+P(t)+C(t)+J(t)+R(t)=1.
Letσdenote the rate of the flow from the non-impoverished class to the impoverished class.It is assumed thatσis omnipresent and dependent upon the unemployment rate because of the nature of unemployment and because of the dependency of poverty on unemployment.Letγdenote the conversion rate from thePclass to theRclass due to government interventions;ρdenote the rate at which criminals are captured andεdenote the fraction of these criminals who ended up in jail;δdenote the rate at which individuals get out of jails;μdenote the rate at which individuals enter and exit the populstion.All rates are per capita and are positive constants.The interaction between poverty and crime is governed by the following system of differential equations:
(1)
Here‘′’ denotes d/dt.The model assumes that there is a certain probability that a person in thePclass will resort to crime after coming into contact with a criminal.The termβPCis the conversion of impoverished individuals to criminals due to contact over a certain period of time,andβrepresents the “transmission” rate.A recovered individual may also become criminal again but at a reduced rateφβRCwhere 0≤φ≤1 is the reduction fraction that accounts for recidivism.According to the report from Bureau of Justice Statistics,about two-thirds (67.8%) of released prisoners were arrested for a new crime within 3 years,and three-quarters (76.6%) were arrested within 5 years[16].The assumption is that those who have already gone to jail and entered theRclass may revert back to criminality at some reduced rateφβdue to contact with criminals.The rate is reduced because these people have a greater cost to commit their next crime,according to Becker′s theory[1].A list of all variables and parameters are provided in Table 1.

Table 1 Definition of symbols frequently used in the model analysis and simulations.All rates are per-capita
3 Mathematical analysis
In this section we derive threshold conditions that determine the population dynamics of the system (1),and these threshold conditions can be helpful for identifying crime control strategies.
LetRdenote the reproduction number of criminals,which is defined as the number of secondary criminal cases generated by one typical criminal individual during the entire period of criminality when introduced into a non-impoverished population.It can be calculated from model (1) that the reproductive number is given by
R=RP+RR,
(2)
where
(3)
RPandRRrepresent the contributions from thePandRclasses,respectively.The factorsβ/(ερ+μ) andφβ/(ερ+μ) give the numbers of new criminals from thePandRclasses,respectively,produced by one criminal individual during the entire criminal period before being captured.The factorσ/(σ+μ) gives the probability that a non-impoverished individual survived and entered the impoverished class whileμ/(γ+μ) andγ/(γ+μ) represent respectively the probabilities that aPindividual remains in thePclass or has moved into theRclass.As shown below,R=1 is a threshold value which determines whether the population size of criminals will go to zero or establish at a positive equilibrium ast→∞.This is shown by studying the existence and stability of equilibria of the system (1).
System (1) always has the crime-free equilibrium (CFE),denoted byE0=(N0,P0,C0,J0,R0):
(4)
LetE*= (N*,P*,C*,J*,R*) withC*>0 denote the positive crime activity at an equilibrium.Setting the right-hand-side of equations in (1) equal to zero we can express all components ofE*in terms ofx=C*:
(5)
Using the fact thatN+P+C+J+R=1 (and noting thatN*=μ/(σ+μ)),we get the equation forx:
(6)
or equivalently
(a2x2+a1x+a0)x=0,
(7)
where
(8)
Equation (7) has one solutionx=0 and two other solutions,which we denote byx±,given by
Notice thata2>0 for all parameter values.The sign ofa0depends on the magnitude ofR.We consider two cases.
Case1R>1.In this case,a0<0 anda0a2<0.Hence,x-is always negative whilex+is always positive.It follows that equation (7) has a unique positive solution;and thus,there is a unique positive equilibriumE*.
Case2R<1.In this case,a0>0 anda0a2>0.If the duration in the poverty class 1/γis smaller than the total duration in the population 1/μ(which is true in general) and
(9)
(note thatRR
Result1WhenR>1,system (1) has a unique crime equilibriumE*.WhenR<1 and condition (9) holds,there is only the CFEE0.
We proceed to show the stability of the equilibria.At the CFE,E0,the Jacobian matrix is
(10)
J(E0) has four negative eigenvaluesλ1=-(σ+μ),λ2=-(γ+μ),λ3=-(δ+μ),λ4=-μ,and the fifth eigenvalue is given by
λ5=(ερ+μ)(R-1).
Hence,all eigenvalues ofJ(E0) are negative ifR<1,andJ(E0) has one positive eigenvalue ifR>1.Fig.1(a) plots the numerical solutions of system (1) for the caseR<1.We observe that C(t)→0 ast→∞.Fig.1(b) is for the caseR>1.It shows that the solution converges to a positive steady state,showing thatE0is unstable.Thus,the following result holds.
Result2The CFE equilibriumE0is locally asymptotically stable (l.a.s.) ifR<1,and it is unstable ifR>1.
The characteristic equation for the crime equilibriumE*is a degree 5 polynomial for which it is difficult to obtain analytical results.We explore the stability ofE*numerically.Fig.1(b) is a time plot of numerical solutions of system (1) for the caseR>1.It shows that the solution converges toE*ast→∞.The parameter values used are:β= 2.8,φ= 0.1,μ= 0.1,σ= 0.5μ,δ= 1/5,ε= 0.7,ρ= 0.2,γ= 0.25.TheRvalues are 0.99 (β=2) in (a) and 1.4 (β=2.8) in (b).

Figure 1 Time plots of the solutions of system (1) forR<1 (see (a)) andR>1 (see (b)) It illustrates that solutions converge to either the crime-free equilibriumE0ifR<1 or the crime equilibriumE*ifR>1 ast→∞.

Figure 2 Phase portrait projected to the (P,C) plane for R>1.It shows that solutions converge to E* (marked by the solid circle) as t→∞
The stability ofE*whenR>1 is also demonstrated in the phase portrait shown in Fig.2,which projects the solutions onto the (P,C) plane for various initial conditions.We observe that all solutions converge toE*ast→∞.The parameter values are the same as in Fig.1(b).We have also run simulations of system (1) for a wide range of parameter values andE*is stable in these cases.
Result3Based on numerical simulations for a wide range of parameter values,the crime equilibriumE*is stable whenever it exists.
The existence and stability results of the equilibrium points of system (1) provide conditions that can be used to evaluate crime control policies and identify cost-effective strategies,as demonstrated in the next section.
4 Cost-effective crime control strategies
Assume that the population has stabilized at the positive equilibriumE*,which implies the assumption thatR>1 based on the analysis in the previous section.In this case,the density of poverty class is
and the density of criminal class isC*withC*=x+being the positive solution of equation (7).The parameters representing crime control and intervention areγ(conversion rate fromPtoR) andρ(criminal capture).Clearly,the reproduction numberRas well asP*=P*(γ,ρ) andC*=C*(γ,ρ) are functions ofγandρ.Fig.3 shows the dependence ofR(the surface plot on the left) and the crime levelC*(the surface plot on the right) onγandρ.The parameter values used are:β= 2,φ= 0.1,μ= 0.1,σ= 0.5μ,δ= 0.5,ε= 0.1.The lighter plane in theRandC*plots corresponds toR=1 andC*=0,respectively.Thus,for all values ofγandρsuch thatR(γ,ρ)<1,there is no equilibrium with positiveC*.

Figure 3 The 3D plots of the reproduction number R (left) and the crime level C* (right) as a function of intervention parameters γ and ρ.The lighter plane represents R=1 (left) and C*=0 (right).It illustrates that C*>0 only for the values of γ and ρ such that R(γ,ρ)>1.

Figure 4 Contour plot of the crime level at the positive equilibrium C* as a function of γ and ρ.The solid circle corresponds to the baseline values γ0 and ρ0,for which the criminal level is 0 level curve identifies the region (shaded) in the (γ,ρ) plane in which the crime level will fall to zero.

Although different combinations ofγandρcan be used to obtain a given level of crime activity,the costs associated with these control measures might be very different,some of which can be higher than the background cost C0while others lower.Thus,a better strategy would lower the cost without increasing the crime activity.There are various ways to compute the cost associated with the control measures.For the purpose of demonstration,we consider a particular cost function.The similar approach can be used for other cost functions.Denote the total cost under the current policy (γ0,ρ0) by C0while all other parameters are being fixed.When we vary the control parametersγandρ,the total cost,which we denote by C(γ,ρ),includes the cost associated with efforts for converting poverty individuals (P) to recovered class (R),the cost of efforts related to capturing criminals,as well as the cost of crimes (to the society or the victims).An example of such function can be defined as

(11)

Fig.5 plots the cost function given in (11).Fig.5(a) shows the surface of C(γ,ρ) in relation to the baseline cost C0(the darker plane),and Fig.5(a) plots the contour curves.The solid circle identifies the points corresponding to the baseline values (γ0,ρ0),and the dashed curve corresponds to the intersection of the surface C(γ,ρ) with the C0plane.That is,the costs are the same for all values ofγandρalong the dashed curve.The dotted curve is another level curve along which the cost has the same value and it is lower than C0.
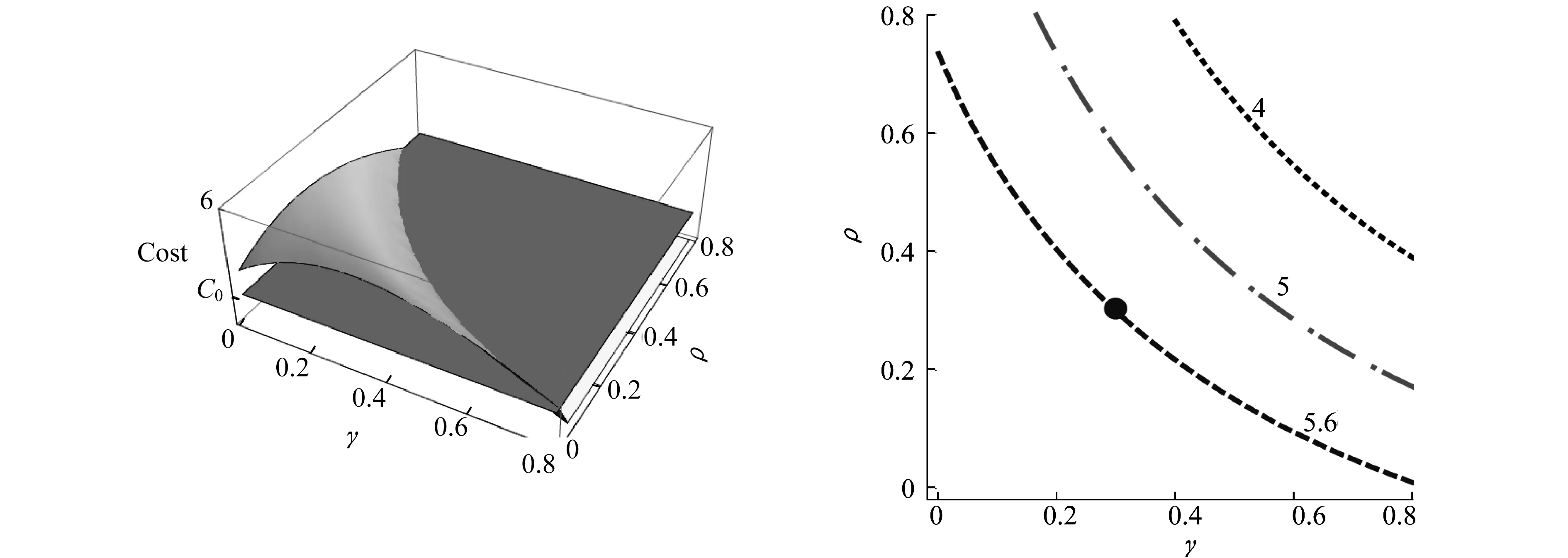
Figure 5 Cost as a function of intervention parametersγandρ.The left figure indicates the region in the (γ,ρ) plane where the cost function C(γ,ρ) (the lighter surface) is below the cost function C0(the darker plane).The figure on the right is a contour plot showing three curves.The dashed curve corresponds to C(γ,ρ)=C0=5.6.For or all (γ,ρ) above this dashed curve,C(γ,ρ) To idenitify new intervention strategies in comparison with current policy,we consider the following two scenarios: Strategy(I) A reduced criminal level without increasing the cost,i.e., Strategy(II) A lreduced costCthat can lead to possible elimination of crime activity,i.e., C(γ,ρ) As mentioned earlier,the control strategies may depend on the constantsBiandwiin the cost function (11).Variations of the relative magnitudes of these constants can lead to different strategies.For example,in the case whenB1(cost per criminal) is small,the dependence of the total cost onγandρis shown in Fig.7.There are several features that are qualitatively different from the case shown in Figs.5 and 6.Because of the lower cost of crimes (B1),the benefits from convertingPtoR(effect ofγ) and capturing criminal (effect ofρ) are reduced.Thus,the total cost rises dramatically with increasedγandρ(see the 3D surface on the left),which is opposite of the case shown in Fig.5.This also affects the relative roles ofγandρwhen considering the reduction of crime activities without changing the baseline cost.As shown in the contour plot (right),for (γ,ρ) along the cost curve (dashed) withγ>γ0andρ<ρ0,the cost curve is below the crime curve (thick solid),indicating a higher crime activity.The parameter values used are the same as in Fig.6 except thatw1B1=5,w2B2=20 andw3B3=200. In this paper we developed a mathematical model to study the dynamics of poverty and crime.By studying the property of equilibria and their stability we derived threshold conditions which can be used to determine the prevalence and control of the crime activity.That is,the dynamics of the model depend on the reproductive numberR.WhenR< 1,the crime level will always fall to zero,whereas whenR> 1,the crime will be persistent (see Results 2,3 and Fig.3).Therefore,our analysis on cost-effective control is only concerned with the caseR> 1.When the crime activity is persistent we explored the possibility of crime control via government interventions (represented by the parametersγandρ) without increasing the total cost associated with the crime activity under a baseline (e.g.,status quo) intervention program (represented byγ0andρ0).We demonstrated that under certain conditions crime control strategies can be identified (see,for example,Figs.6) if all the relevant cost and weight constants (Biandwi) are known. We presented two examples to show how a cost-effective control strategy can be identified for a give set of parameter values.These examples illustrated that for different populations and under different conditions (determined by the baseline valuesγ0andρ0as well as the cost and weight constantsBiandwi),the cost-effective strategies can be very different (see Figs.6 and 7). The implications of the model are what we expected.Naturally,eliminating all crime is not feasible.The model together with the cost function show that,for a given crime level,there will be optimal values of the parametersγandρ,such that the cost of controlling crime is at a minimum.Note that we have only suggested one cost function,which is given in (11).Other forms of cost functions can be formulated depending on the particular factors associated with the population under investigation,including the poverty and crime situations,and the specific constraints for the costs of crime control and intervention,among other considerations. : [1] Gary S Becker.Crime and punishment:An economic approach[J].Journal of Political Economy,1968,76:167-217. [2] Marcel Fafchamps and Bart Minten.Crime and poverty:Evidence from a natural experiment[M].University of Oxford Centre for the Study of African Economies,2002. [3] Morgan Kelly.Inequality and crime[J].Review of Economics and Statistics,2000,82(4):530-539. [4] W Henry Chiu,Paul Madden.Burglary and income inequality[J].Journal of Public Economics,1998,69(1):123-141. [5] U.S.Department of Justice,Federal Bureau of Investigation.Uniform crime reports:Crime in the united states.Accessed May 6,2014.http://www.fbi.gov/about-us/cjis/ucr/crime-in-the-u.s/2010/crime-in-the-u.s.-2010/property-crime. [6] Newsday.Crime in New York City 2009-2013[OL/J].Accessed May 7,2014.http://data.newsday.com/long-island/data/crime/new-york-city-crime-rate/. [7] US Census Bureau.State & county quick facts[OL/J].Accessed May 7,2014.http://quickfacts.census.gov/qfd/states/36/36005.html. [8] Mark Acohen.The costs of crime and justice[M].Routledge,2012. [9] National Institute of Justice.Victim costs and consequences:A new look[OL/J].Accessed May 7,2014.https://www.ncjrs.gov/pdffiles/victcost.pdf. [10] David A Anderson.The aggregate burden of crime[J].The Journal of Law and Economics,1999,42(2):611-642. [11] Isaac Ehrlich.On the usefulness of controlling individuals:An economic analysis of rehabilitation,incapacitation and deterrence[J].The American Economic Review,1981,pages 307-322. [12] Federal Bureau of Prisons.Federal prison system per capita costs fy 2012.Accessed May 7,2014.http://www.bop.gov/foia/fy12_per_capita_costs.pdf. [13] Isaac Ehrlich.Participation in illegitimate activities:A theoretical and empirical investigation[J].Journal of Political Economy,1973,81(3):521-565. [14] Ann Dryden Witte.Estimating the economic model of crime with individual data[J].The Quarterly Journal of Economics,1980,94(1):57-84. [15] Michael K Block,John M Heineke.A labor theoretic analysis of the criminal choice[J].American Economic Review,1975,65(3):314-325. [16] Alexia D C,Matthew R D,Howard N S.Recidivism of prisoners released in 30 states in 2005:Patterns from 2005 to 2010[OL/J].BJS,2014,http://www.bjs.gov/index.cfm?ty=pbdetail iid=4986. [17] Kathryn E Mccollister,Michael T French,Hai Fang.The cost of crime to society:New crime-specific estimates for policy and program evaluation[J].Drug and Alcohol Dependence,2010,108(1):98-109. [18] U.S. Department of Justice,Federal Bureau of Investigation.Uniform crime reports:Crime in the united states.Accessed May 6,2014.http://www2.fbi.gov/ucr/cius2007/.

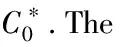

5 Discussion



