平方根随机自回归波动模型及其性质研究

张 超, 孟昭为

(山东理工大学 理学院, 山东 淄博 255091)

一般线性GARCH过程在时间聚合下并不封闭，因而提出弱GARCH过程概念，而弱GARCH过程关于时间聚合不论是存量或流量都是封闭的.虽然弱GARCH过程的引入解决了GARCH过程在时间聚合下的封闭问题，但仍存在许多不足.文献[1]基于半参数方法，提出了平方根随机自回归波动模型(square-root stochastic autoregressive volatility，SRSARV)，它是弱GARCH模型的自然扩展，不仅克服了弱GARCH模型的很多不足，而且还具有很多方面的优良性质.

1 SRSARV模型定义

1.1 离散SRSARV模型

定义1[1-4]平稳平方可积过程{εt,t∈Z}称为是关于递增过滤集Jt,t∈Z的SRSARV(p)过程，如果

① 过程εt适应于过滤集Jt;

② 过程εt是关于过滤集Jt-1的鞅差分序列,即E[εt|Jt-1]=0;

③ 给定Jt-1时,εt的条件方差过程ft-1是p维平稳的Var(1)过程Ft-1的边际化：

ft-1=Var(εt|Jt-1)=eTFt-1

(1)

Ft=Ω+ΓFt-1+Vt

(2)

E[Vt|Jt-1]=0

(3)

式中e∈Rp,Ω∈Rp为含有非负元素的非零向量.为了保证Ft的平稳性和模型的正定性，要求Γ的特征根的模小于1，且Ω中的元素具有非负性.

定义2[1-4]平稳平方可积过程{εt,t∈Z}称为是关于递增过滤集Jt,t∈Z的SRSARV(∞)过程，如果

① 过程εt适应于过滤集Jt;

② 过程εt是关于过滤集Jt-1的鞅差分序列,即E[εt|Jt-1]=0;

③ 在给定Jt下，εt的条件方差过程ft-1满足

(4)

其中序列{fi,t-1,t∈Z,i∈N}满足：

ⓐ∃q，使向量Fq,t=(f1,t,…，fq,t)T服从一个平稳的Var(1)过程

E[Fq,t|Jt-1]=Ωq+ΓqFq,t-1

(5)

并与fn,t(n>q)不相关，且Γq的特征根在单位圆外；

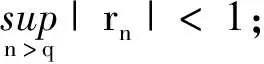
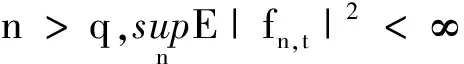
如果严格的说(4)式所表达的实际上就是条件方差为无线维Ft≡(f1,t,f2,t,…)T的边际化，其中Var(1)过程可表示为E[Ft|Jt-1]=Ω+ΓFt-1，从而是对定义(1)的扩展.

1.2 连续SRSARV模型

(6)

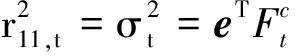
2 主要性质及证明

2.1离散SRSARV过程是连续SRSARV过程的精确离散化

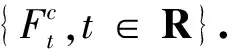
证明由公式(6)得

式中W1t是Wt的一阶矩.因此有

与

由公式(6)我们还可以得到

其中M22=(0,Ip)是p×(p+1)的矩阵.那么有

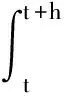
(7)

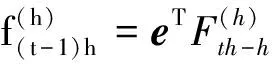
其中A(h)=K-1(Id-e-Kh)，B(h)=(hId-A(h))Θ.

2.2 SRSARV模型的平方新息的ARMA表达

与传统的波动模型如(G)ARCH类模型、SV类模型相似，SRSARV模型的平方新息也具有ARMA表达形式，因此产生了一类丰富的自回归模型.

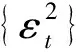
(8)

其中{ωt}是一个MA(p)过程，且有

E[ωt|Jt-p-1]=0

(9)

2.3 SRSARV模型的多期条件矩限制

(10)

该条件称为多期条件矩限制，可用于检验一个平稳过程有无SRSARV(p)表示.

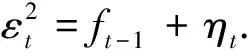
Ft=Ω+ΓFt-1+Vt

⟹(Id-ΓL)Ft=Ω+Vt

⟹Det(Id-ΓL)Ft=(Id-ΓL)*(Ω+Vt)

其中L是滞后算子，Det(·)是行列式函数，(Id-ΓL)*是(Id-ΓL)的伴随矩阵.故得

Det(Id-ΓL)ft=Det(Id-ΓL)eTFt=

eT(Id-ΓL)*Ω+eT(Id-ΓL)*Vt

由Deg(eT(Id-ΓL)*)≤p-1，其中Deg(·)是最大维度的滞后多项式系数矩阵,故有

E[Det(Id-ΓL)ft-eT(Id-ΓL)*Ω|Jt-p]=0

我继续问宇轩：“你又看到了什么？”宇轩以为前两位说的都不对，想了想说：“我什么都没有看到。”全班同学都笑了，有的同学还指着黑点说：“明明有黑点，难道你看不见吗？”

因此得

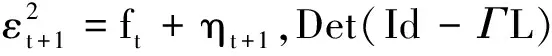
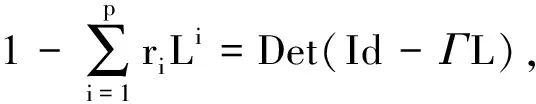
(2)充分性

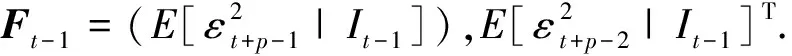
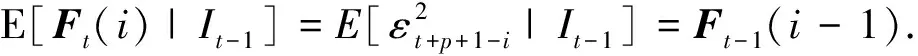
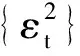
2.4 SRSARV模型的杠杆效应和偏度

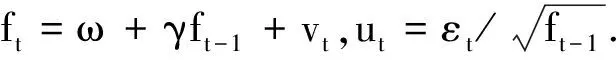
①εt不具有关于递增过滤集Jt的杠杆效应，当且仅当

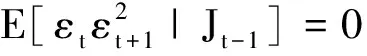
(11)

②εt不具有关于递增过滤集Jt的偏度，当且仅当

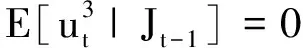
(12)

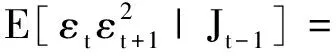
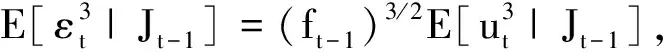
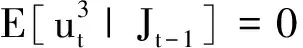
[1] Meddahi N,Renault E.Temporal aggregation of volatility models[J].Journal of Econometrics,2004,119:355-379.

[2] Andersen T G. Stochastic autoregressive volatiliey:a framework for volatility modeling[J].Mathematical Finance,1994,4(2):75-102.

[3] 杜子平,张世英.SV模型的聚合及边际化研究[J].系统工程理论方法应用,2002,11(2):173-176.

[4] 许启发,张世英.金融波动的平方根随机波动模型[J]. 系统工程理论方法应用,2004,13(6):561-568.

[5] 詹姆斯·D·汉密尔顿.时间序列分析[M].北京：中国社会科学出版社,1999.

[6] Duan J C.Augmented GARCH(p,q) process and itsdiffusion limit[J]. Journal of Econometrics,1997,79:97-127.

[7] Linden M.Time series properties of aggregated AR(1) processes with uniformly distributed coefficients[J].Economics Letters,1999,64:31-36.