三维位势直接边界元法中的几乎奇异积分

李小超， 张耀明

(山东理工大学 理学院， 山东 淄博 255091)

三维直接边界元法的有效实施要求准确计算各种核积分.当源点属于积分单元时，这些核函数是奇异的，对此已有许多有效的处理方法[1-3].另一个重要的问题是源点接近但不在积分单元上的核积分的计算.理论上，这样的积分是非奇异的，但是它们又表现出类似奇异性的特征，通常不能通过标准的高斯公式准确计算，称之为几乎奇异积分.不同于常规积分，几乎奇异积分需要特别的处理方法.本文着眼于三维边界元分析中高阶几何单元上的几乎奇异积分的数值解法研究.

边界元分析中，一般地认为，准确计算几乎奇异积分的重要性仅次于奇异积分，近年来引起了许多学者的关注，发展了许多数值处理技术和方法，如刚体位移法[3]、区间分割法[4]、解析与半解析法[5]及各种非线性变换法[6-10]等，文献[6]对此进行了较全面的综述.在这些方法中，变换法具有方法简单、效率高、适用范围广等优点，是目前较盛行的方法，包括：三次多项式变换[7]、Sinh变换[8]及指数变换[9-11]等.

文献[11]提出了一种非线性指数变换法来处理几乎奇异积分，并将其应用在处理三维弹性问题中，取得了理想的结果.本文将文献[11]提出的变换法与三维直接变量规则化边界积分方程相结合，来处理三维位势问题中的几乎奇异积分.数值算例表明，本文算法稳定、效率高，即使计算点非常靠近真实边界，使用较少的离散单元就可获得令人满意的计算结果.

1 二边界积分方程中的几乎奇异积分

考虑三维位势问题，区域内点y的位势及其导数边界积分方程可写为

(1)

(2)

式中q(x)为场点x的法向位势梯度，u(x)为场点x的位势.u*(x,y)为三维位势基本解，q*(x,y)为位势基本解对边界外法线的梯度.yk为源点y坐标.离散积分式(1)，(2)所使用的基本核函数有

(3)

式中r为源点y到边界上场点x的距离.

对于方程(1)与(2)的离散化形式，当计算点y非常靠近积分单元Γe时，计算点y与积分单元Γe之间的距离非常地小，几乎接近于零，此时方程(1)与(2)中的积分核将产生不同程度的几乎奇异性，直接应用标准的高斯求积公式不能准确求解.这些几乎奇异积分可以表示为

(4)

式中r=‖x-y‖2，α>0为常数，f(x,y)是一个规则函数，在不同的积分中可能不同.

2 高阶几何单元的几乎奇异积分

(5)

这里Nj(ξ1,ξ2)(j=1,…，8)是插值形函数,ξ1,ξ2是无因次坐标

距离函数r2可表示为

r2(ξ1,ξ2)=d2+(ξ1-η1)2g11+

(ξ2-η2)2g22+(ξ1-η1)(ξ2-η2)g12

(6)

3 几乎奇异积分的变量替换

针对方程(4)中的几乎奇异积分，考虑如下指数变换

x=d(em1+m2s-1),y=d(en1+n2t-1),

-1≤s≤1,-1≤t≤1

(7)

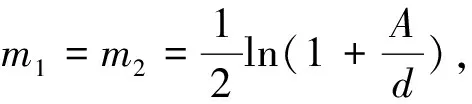
将式(7)代入式(4)中，可得

(8)

式中

F(s,t)=[1+(em1+m2s-1)2g11(x,y)+

(en1+n2t-1)2·g22(x,y)+

(em1+m2s-1)(en1+n2t-1)g12(x,y)]α

变换后的积分(8)可直接应用高斯求积公式计算.下节中的数值算例验证了本文所提算法的有效性.

4 数值算例

例1考虑三维球域的热传导问题.如图1所示，该球域半径为1，表面温度已知，可以表示为

图1 单位球域划分为100个二次曲面单元

该三维球域表面划分为100个二次曲面单元，边界量采用二次不连续插值型函数近似.表1、表2分别列出了沿x1方向内点处的位势u以及位势梯度∂u/∂x1的数值结果.可以看出，当计算点距离边界不是很近时，使用传统边界元法(未加变换)或是本文方法均能得到令人满意的结果；然而，随着所取得计算点趋于边界，当计算点到边界的距离小于0.001时，传统边界元法已经失效.另一方面，即使所取的计算点到边界的距离达到1×10-10，使用本文方法依然可以取得准确的结果.由此表明本文算法在处理几乎奇异积分是非常有效的.

上，根据坐标θ与φ，均匀选取400个内点进行计算.图2 (a)、(b)则给出了这400个内点处的相对误差曲面，位势u与位势梯度∂u/∂x1的平均相对误差分别为8.7705×10-4、2.2353×10-3.这个数值结果进一步表明本文算法在处理几乎奇异积分是的准确性与有效性.

表 1近边界点位势u的计算结果

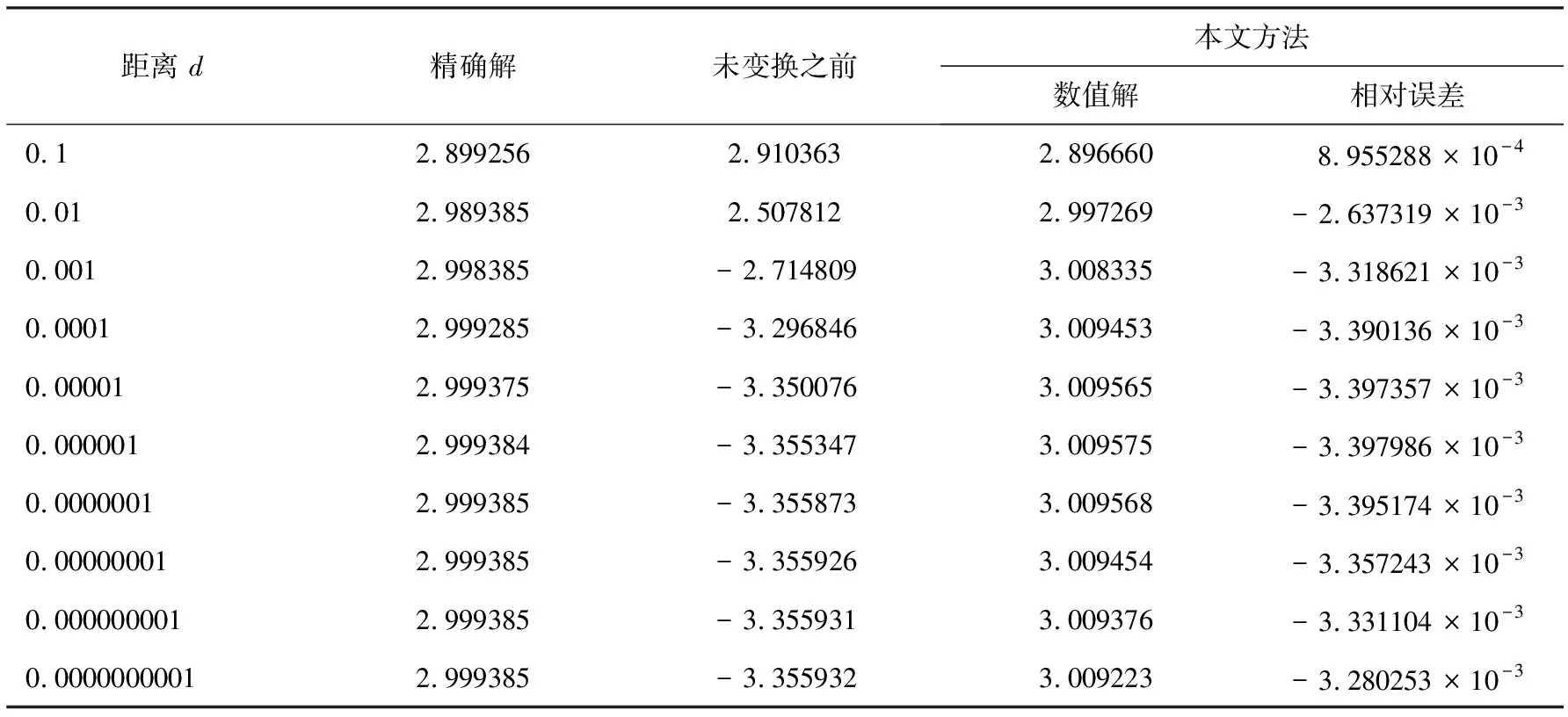
表 2近边界点位势梯度∂u/∂x1的计算结果

5 结束语

针对三维位势直接边界元法中的几乎奇异积分，本文利用一种非线性指数变换法，使用高阶几何单元来描述复杂几何边界；构造了新的距离函数；利用拓展的变换来消除被积函数的几乎奇异性.数值算例表明，本文算法稳定、效率高，即使计算点十分靠近边界，仍可获得令人满意的计算结果.

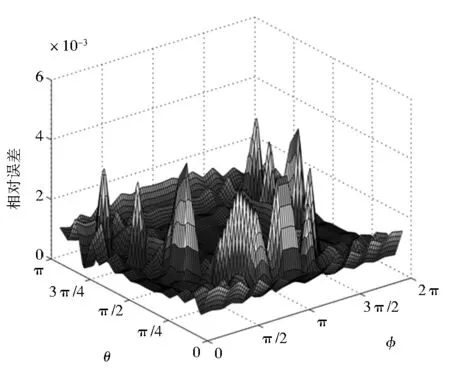
(a)位势

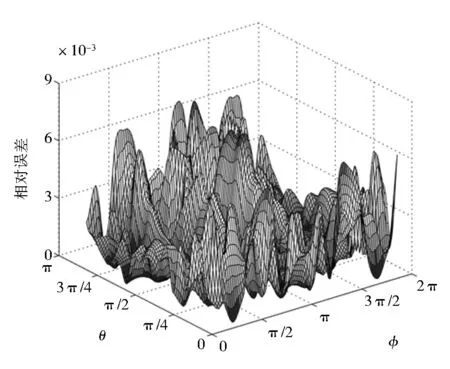
(b)位势梯度图2 400个内点处位势与位势梯度的相对误差曲面

[1] Tanaka M, Sladek V, Sladek J. Regularization techniques applied to boundary element methods[J]. Applied Mechanics Reviews, 1994, 47: 457-499.

[2] Liu Y J. On the simple solution and non-singular nature of the BIE/BEM-a review and some new results[J]. Engng. Anal. Bound. Elem.,2000, 24: 286-292.

[3] Sladek V, Sladek J, Tanaka M. Regularization of hypersingular and nearly singular integrals in the potential theory and elasticity[J]. Int. J. Numer. Meth. Engng, 1993, 36(10): 1 609-1 628.

[4] Gao X W, Yang K, Wang J. An adaptive element subdivision technique for evaluation of various 2D singular boundary integrals[J]. Engng. Anal. Bound. Elem., 2008, 32: 692-696.

[5] Zhang X S, Zhang X X. Exact integrations of two-dimensional high-order discontinuous boundary element of elastostatics problems[J]. Engng. Anal. Bound. Elem., 2003, 28(7): 725-732.

[6] 张耀明, 孙翠莲,谷岩.边界积分方程中近奇异积分计算的一种变量替换法[J]. 力学学报, 2008, 40(2): 207-214.

[7] Telles J C F. A self-adaptive coordinate transformation for efficient numerical evaluation of general boundary element integral[J]. Int. J. Numer. Meth. Engng, 1987, 24: 959-973.

[8] Johnston P R, Elliott D. A sinh transformation for evaluating nearly singular boundary element integrals[J]. Int. J. Numer. Meth. Engng.,2005, 62: 564-578.

[9] Zhang Y M, Gu Y, Chen J T.Boundary element analysis of the thermal behaviour in thin-coated cutting tools[J]. Engng. Anal. Bound. Elem.,2010, 34(9): 775-784.

[10] Gao X W, Davies T G. Adaptive algorithm in elasto-plastic boundary element analysis[J]. Journal of the Chinese Institute of Engineers, 2000, 23(3): 349-356.

[11] 张耀明，李小超，Sladek V，等. 三维边界元法中高阶几何单元上的几乎奇异积分[J].力学学报，2013, 45(6): 908-918.