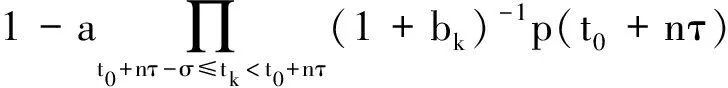一类非线性脉冲时滞差分方程的振动性

葛礼霞

(牡丹江师范学院 理学院, 黑龙江 牡丹江 157012)

关于差分方程的振动性已有许多学者进行了研究，且对具有连续变量的差分方程振动性的研究取得了大量的成果，如文献[1-4]建立了具有连续变量的差分方程振动的充要条件.文献[5]给出了如下具有连续变量的非线性时滞差分方程

y(t+τ)-y(t)+p(t)f(y(t-σ))=0

的振动性的充分条件.文献[6-9]研究了脉冲时滞微分、差分方程的振动性.

考虑如下一类具有连续变量的变系数脉冲时滞差分方程的振动性

(1)

x(t)=x(t,t0,φ),t∈[t0-r,t0]

(2)

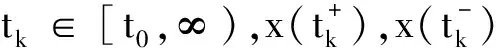
(3)

方程(3)满足初始条件(2)的解y(t)，当t∈[t0-r,t0]时，y(t)=φ(t)，当t∈[t0,∞)时，y(t)是绝对连续的，且它在[t0,∞)上几乎处处满足方程(3).我们利用构造函数的方法，讨论这一类具有连续变量的变系数脉冲时滞差分方程的振动性.

1 引理

引理1[6]若存在自然数K，使当k>K时有bk>-1，则方程(1)的所有解振动，当且仅当(3)的所有解振动.

2 主要结果

定理1设bk>0，对所有k=1,2,…成立，若

(i)存在常数δ>0，使

f(u)sgnu≥δ

(4)

(ii)对任意的t≥0，有

(5)

则方程(1)所有解振动.

证明由引理可知，只需证方程(3)振动.

用反证法.不失一般性，设方程(3)有一个最终正解y(t)，则存在t1>0，使得当t≥t1时，有

y(t)>0,y(t-τ)>0,y(t-σ)>0

因f(u)sgnu≥δ，有

f(y(t-σ))≥δ

(6)

特别地，对于i=1,2,…，n，有

上式两边对i从1到n求和，得

(7)

由(5)式和(7)式可得

这与y(t)是最终正解矛盾，故方程(1)无最终正解.综上可知，方程(1)的所有解振动.

定理2设bk>0，对所有k=1,2,…成立，且σ=kτ,k≥2为正整数，若

(i)f(u)单调非减，且当

u≠0,uf(u)>0

(8)

(ii)对任意的t≥0，有

(9)

(10)

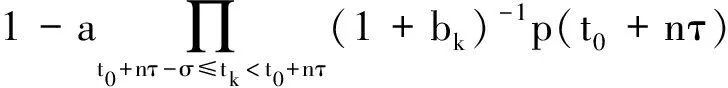
证明由引理可知，只需证方程(3)振动.

用反证法.设方程(3)有一个最终正解y(t)，则存在充分大的t0>0，使得当t≥t0时，有

y(t)>0,y(t-τ)>0,y(t-σ)>0

因u≠0,uf(u)>0，有

f(y(t-σ))>0

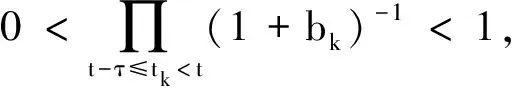
(11)

故有0

下面来证l0=0，若不然，假设l0>0，由y(t0+nτ)≥l0且f(u)单调非减，有

f(y(t0+nτ))≥f(l0)>0

再由该式和(11)式可得

即

将该式对i从1到n求和，得

再由(9)式可得

这与y(t0+nτ)是最终正解矛盾.因此l0=0，即

再结合(10)式可知，存在充分大的自然数n1，使得当n≥n1时，有

由方程(3)得

特别地，有

进而有

本文证明了一类具连续变量的脉冲差分方程的振动性，得到了脉冲时滞差分方程解振动的两个充分条件，将已有文献中的有关结果在脉冲条件下做了推广和改进.

[1] 张友生,庾建设.具连续变量的线性时滞差分方程的振动性[J].高校应用数学学报A辑,2000,15(1):25-33.

[2] 张玉珠,燕居让.具有连续变量的差分方程振动性的判据[J].数学学报,1995,38(3):406-411.

[3] 黄梅,申建华.具连续变量的偶数阶中立型差分方程的振动性[J].纯粹数学与应用数学,2006,22(3):399-404.

[4] 周勇.具有连续变量的变系数差分方程的振动性[J].经济数学，1996,13(1):86-89.

[5] 韩振来.具有连续变量的非线性时滞差分方程的振动性[J].应用数学与计算数学学报,1999,13(1):60-64.

[6] Tang X H,Yu J S.Oscillation and stability of linear impulsive delay difference equations[J].Math Appl,2001,14(1):28-32.

[7] Wei G P, Shen J H. Oscillation of solutions of impulsive difference equations withcontinuous variable[J].Math Appl,2005,18(2):293-296.

[8] 魏耿平,申建华.具连续变量差分方程非振动解在脉冲扰动下的保持性[J].数学物理学报,2006,26A(4):595-600.

[9] 李建利,申建华.二阶脉冲时滞微分方程的振动性[J].系统科学与数学,2010,30(7):990-997.