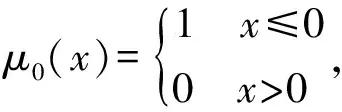热传导方程的修正C-N格式及稳定性分析
何巧玲, 阿布都热西提·阿布都外力
(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)
1 热传导方程及差分格式的构造
考虑热传导方程
(1)
式中:u=u(x,t)是扩散过程中某种物质的浓度,或者固体产热过程中在x处t时刻的温度;f(x),g(t),h(t)是已知函数.
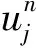
(2)
2 新差分格式的引入
热传导方程的显示格式为
即得
(3)
由(3)式可得
(4)
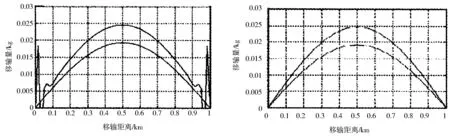
(1)1 (5) 此法为热传导方程显示的五点差分格式. 即 即 (1+r)vn+1=[r2cos2kh+2(r-r2)coskh+1-r+r2]vn 令coskh=t,t∈[-1,1],则 (1+r)vn+1=(2r2t2+2(r-r2)t+1-r)vn 于是格式(5)的稳定性条件为r≤3. 证明格式(5)U(xj,tn)在(xj,tn)对时间变量t进行泰勒展开 (6) 对定解问题 (i)τ=0.008,h=0.0 167,从图(1)可以看到C-N格式(2)虽然是无条件稳定的,但在不连续的边界附近有振动.当然,理论上讲,C-N格式对某些参数的选取会出现计算不稳定、编程复杂、计算量大等缺点. (ii)τ=0.008,h=0.0 334,从图(2)可以看到修正C-N格式(5)满足稳定性条件为r≤3,在不连续的边界附近图像很光滑且没有任何振动,修正C-N格式不会出现不稳定的现象,节省计算工作量而且利用格式本身就可以计算出第一时间层上的值,这就克服了隐格式解线性方程组的缺点.求解热传导方程的显修正C-N格式丰富了数值求解热传导方程的理论方法. 图1 t=0.01时,C-N格式的计算结果和准确值比较 图2 t=0.01时,修正C-N格式的计算结果和准确值比较 本文提出了一种修正Crank-Nicolson法,是r≤3显格方法.结果表明,该方法具有计算简单、稳定性好的优点,是求解热传导方程的有效实用方法. [1] 李德元,晨光南.抛物型方程差分方法引论[M].北京:科学出版社,1995. [2] 热米娜·沙比尔,阿布都热西提·阿布都外力.对热传导方程近似解在边界附近的变化研究[J]首都师范大学学报:自然科学版,2013,34(2):10-13. [3] Harwood R C,Zhang L K,Vogel G M,etal.Oscillation-free operator splitting method for semilinear diffusion equations[J].Journal of Applied Mathematics and Computation,2013,18(7):7-18. [4] 冯青华.四阶抛物方程的一类交替分组方法[J].山东大学学报:理学版,2007,42(8):79-82. [5] 左进明,张天德.五阶色散KdV方程的交替分段显-隐差分格式[J].山东大学学报:理学版,2010,45(10):116-121. [6] 陆金莆,关治编.偏微分方程数值解法[M].3版.北京:清华大学出版社,2003.

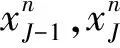
3 五点差分格式的稳定性
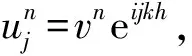
4 关于收敛性定理

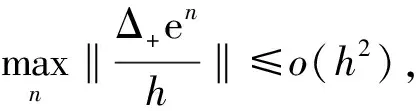
5 数值实验